数据结构与算法:树
目录
树
定义
结构
二叉树
定义
结构
形式
满二叉树
完全二叉树
存储
链式存储结构
数组
孩子节点
父节点
应用
查找
维持相对顺序
遍历
深度优先遍历
前序遍历
中序遍历
后序遍历
广度优先遍历
层序遍历
二叉堆
定义
自我调整
操作
插入加点
删除节点
构建二叉堆
代码实现
优先队列
特点
实现
入队操作
出队操作
树
在实际场景中,有许多逻辑关系并不是简单的线性关系,常常存在一对多、多对多的关系;其中树和图就是典型的非线性数据结构。
定义
树是n(n >=0)个节点的有序集合。当n=0时,称为空树,空树特点:有且仅有一个特定的称为根的节点;当n>1时,其余节点可分为m(m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树
结构
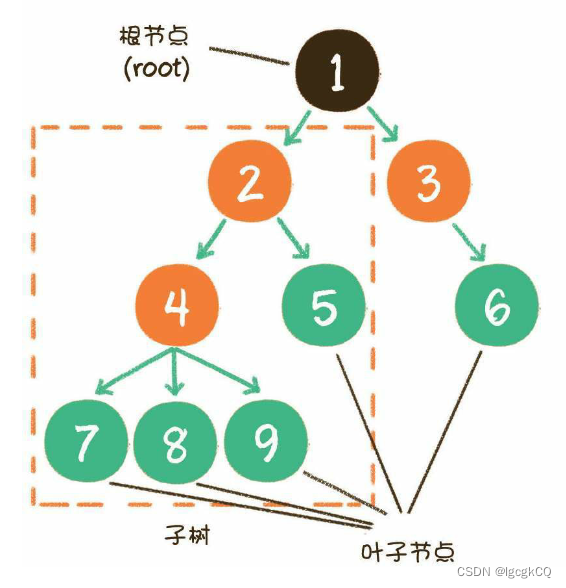
节点1是根节点;节点5、6、7、8、9是树的末端,没有“孩子”,被称为叶子节点。图中的虚线部分,是根节点1的其中一个子树。
树的结构从根节点到叶子节点,分为不同的层级。从一个节点的角度来看,它的上下级和同级节点关系如下:
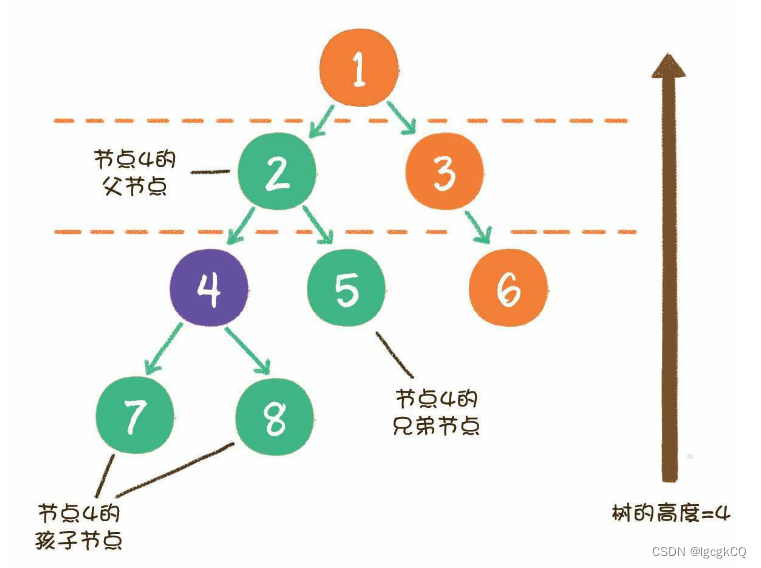
节点4的上一级节点,是节点4的父节点;从节点4衍生出来的节点,是节点4的孩子节点;和节点4同级,由同一个父节点衍生出来的节点,是节点4的兄弟节点;
树的最大层级数,称为树的高度或深度。
二叉树
定义
二叉树是数的一种特殊形式。这种树的每个节点最多有两个孩子节点(最多两个,可以是1个或者0个)。
结构
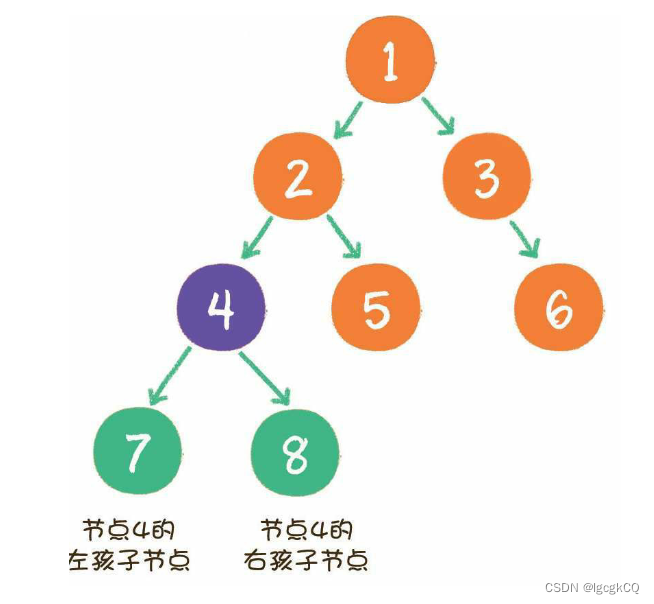
二叉树节点的两个孩子节点,一个被称为左孩子,一个被称为右孩子。这两个孩子节点的顺序是固定的,就像人的左手就是左手,右手就是右手,不能够颠倒或混淆。
形式
二叉树还有两种特殊形式,一个叫作满二叉树,另一个叫作完全二叉树
满二叉树
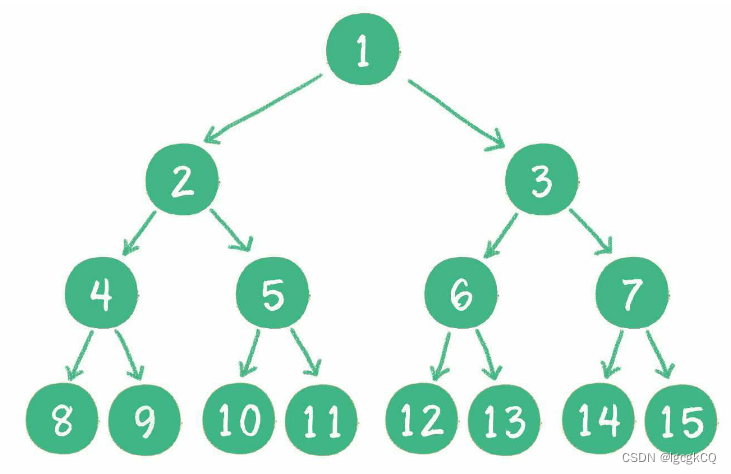
一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树;满二叉树的每一个分支都是满的。
完全二叉树
对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个二叉树为完全二叉树
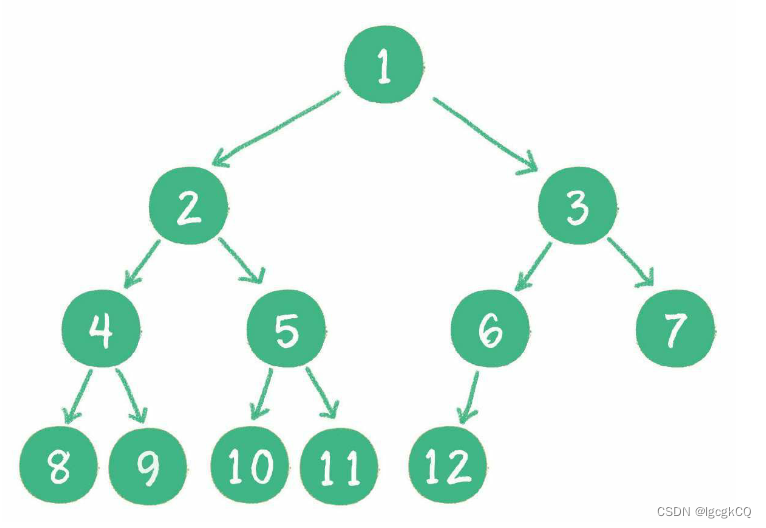
二叉树编号从1到12的12个节点,和前面满二叉树编号从1到12的节点位置完全对应。因此这个树是完全二叉树。
完全二叉树的条件没有满二叉树那么苛刻:满二叉树要求所有分支都是满的;而完全二叉树只需保证最后一个节点之前的节点都齐全即可
存储
数据结构可以分为物理结构和逻辑结构。二叉树属于逻辑结构,它可以通过多种物理结构来表达;
二叉树可以用到链式存储结构和数组两种物理存储结构来表达
链式存储结构
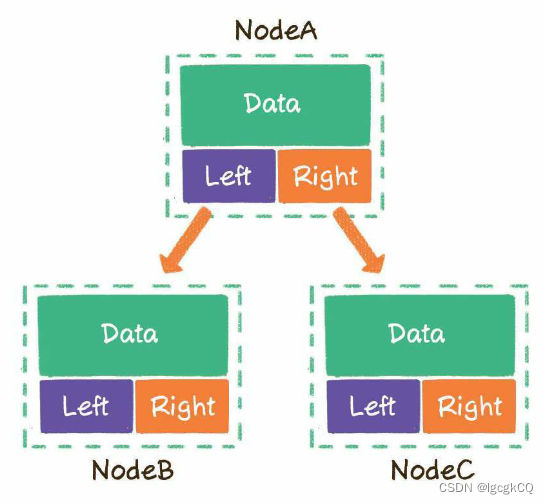
链式存储是二叉树最直观的存储方式;
链表是一对一的存储方式,每一个链表节点拥有data变量和一个指向下一节点的next指针;二叉树稍微复杂一些,一个节点最多可以指向左右两个孩子节点,所以二叉树的每一个节点包含3部分:
1.存储数据的data变量
2.指向左孩子的left指针
3.指向右孩子的right指针
数组
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来,可以更方便地在数组中定位二叉树的孩子节点和父节点
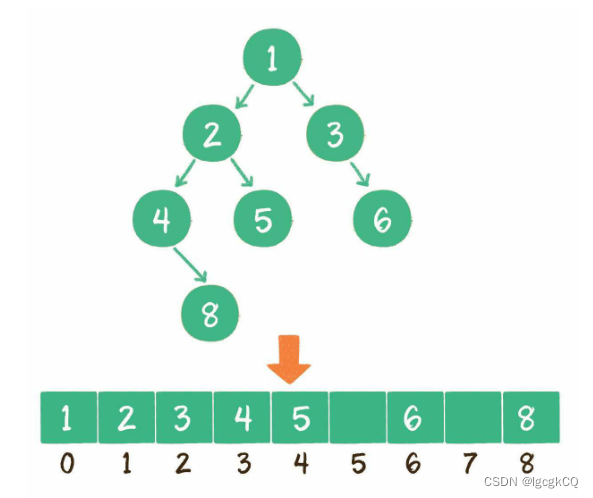
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来。这样可以更方便地在数组中定位二叉树的孩子节点和父节点。
孩子节点
计算:一个父节点的下标是parent,那么它的左孩子节点下标就是2×parent +1;右孩子节点下标就是2×parent + 2。
父节点
计算:一个左孩子节点的下标是leftChild,那么它的父节点下标就是(leftChild-1)/ 2;
对于一个稀疏的二叉树来说,用数组表示法是非常浪费空间的
应用
二叉树包含了很多的特殊形式,每一种形式都有自己的作用,但是最主要的应用还在于查找操作和维持相对顺序两方面。
查找
二叉树的树形结构使它很适合扮演索引的角色。
特殊的二叉树:二叉查找树,主要的作用就是进行查找操作,在二叉树的基础上增加了条件:
1.如果左子树不为空,则左子树上的所有节点的值均小于根节点的值
2.如果右子树不为空,则右子树上的所有节点的值均大于根节点的值
3.左、右子树也都是二叉查找树
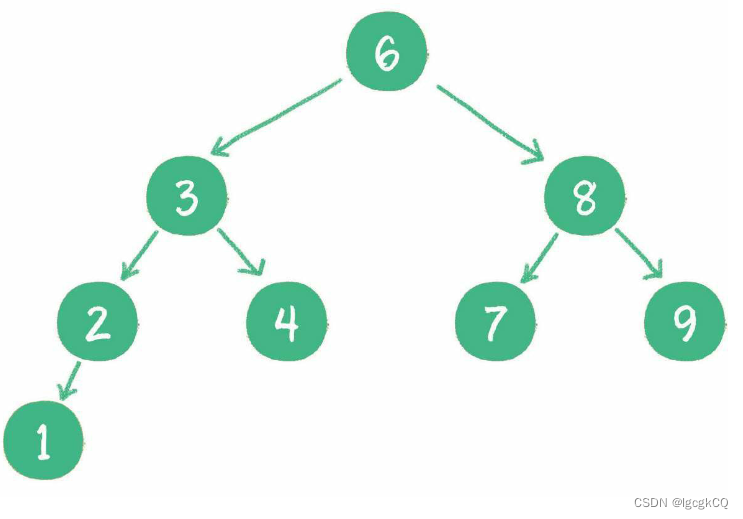
对于一个节点分布相对均衡的二叉查找树来说,如果节点总数是n,那么搜索节点的时间复杂度就是O(logn),和树的深度是一样的。
这种依靠比较大小来逐步查找的方式,和二分查找算法非常相似
维持相对顺序
二叉查找树要求左子树小于父节点,右子树大于父节点,正是这样保证了二叉树的有序性,所以又叫:二叉排序树。
新插入的节点,同样要遵循二叉排序树的原则
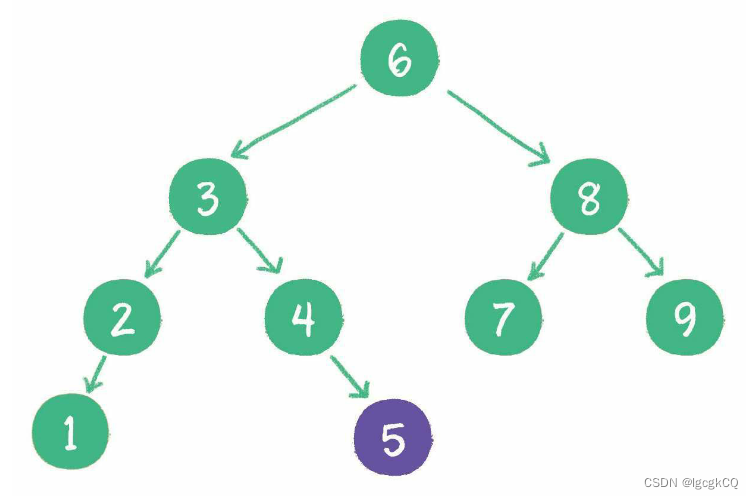
插入新元素5,由于5<6,5>3,5>4,所以5最终会插入到节点4的右孩子位置
遍历
在计算机程序中,遍历本身是一个线性操作。所以遍历同样具有线性结构的数组或链表,是一件轻而易举的事情;
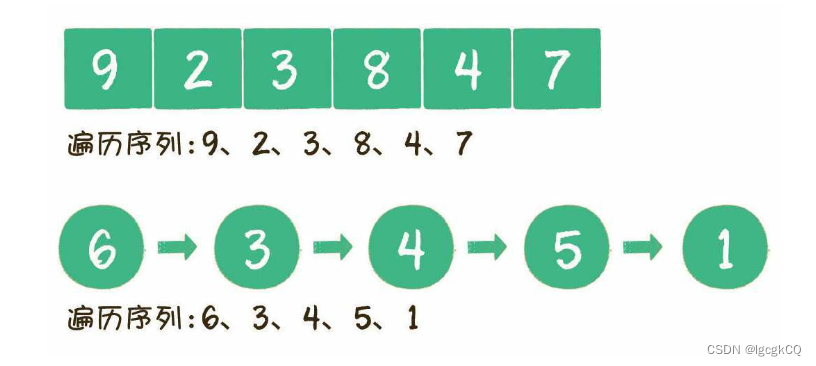
反观二叉树,是典型的非线性数据结构,遍历时需要把非线性关联的节点转化成一个线性的序列,以不同的方式来遍历,遍历出的序列顺序也不同
从节点之间位置关系的角度来看,二叉树的遍历分为4种。
1. 前序遍历。
2. 中序遍历。
3. 后序遍历。
4. 层序遍历
从更宏观的角度来看,二叉树的遍历归结为两大类。
1. 深度优先遍历(前序遍历、中序遍历、后序遍历)。
2. 广度优先遍历(层序遍历)
深度优先遍历
深度优先和广度优先这两个概念不止局限于二叉树,它们更是一种抽象的算法思想,决定了访问某些复杂数据结构的顺序。
所谓深度优先,顾名思义,就是偏向于纵深,“一头扎到底”的访问方式
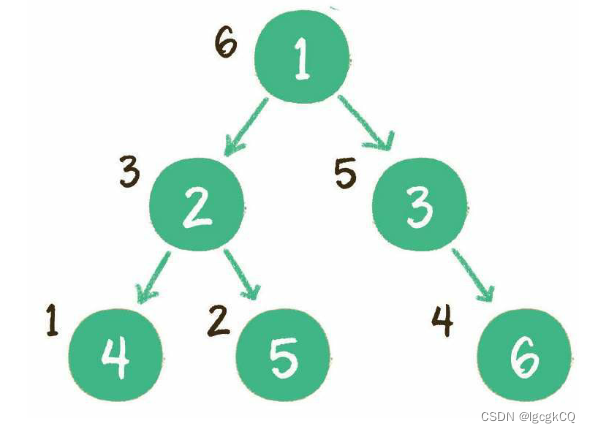
前序遍历
二叉树的前序遍历,输出顺序是根节点、左子树、右子树
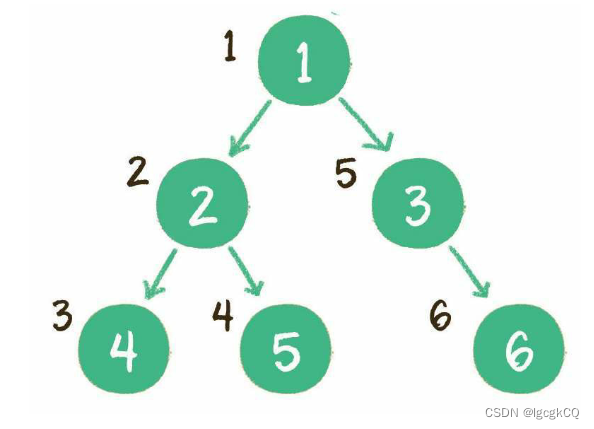
中序遍历
二叉树的中序遍历,输出顺序是左子树、根节点、右子树

后序遍历
二叉树的后序遍历,输出顺序是左子树、右子树、根节点。
广度优先遍历
层序遍历
顾名思义,就是二叉树按照从根节点到叶子节点的层次关系,一层一层横向遍历各个节点
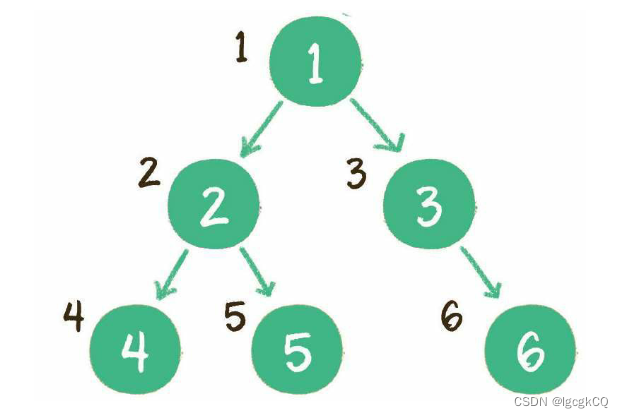
二叉树同一层次的节点之间是没有直接关联的,需要借助一个数据结构来辅助工作,这个数据结构就是队列。
public static void levelOrderTraversal(TreeNode root){Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);while(!queue.isEmpty()){TreeNode node = queue.poll();System.out.println(node.data);if(node.leftChild != null){queue.offer(node.leftChild);}if(node.rightChild != null){queue.offer(node.rightChild);}}
}二叉堆
定义
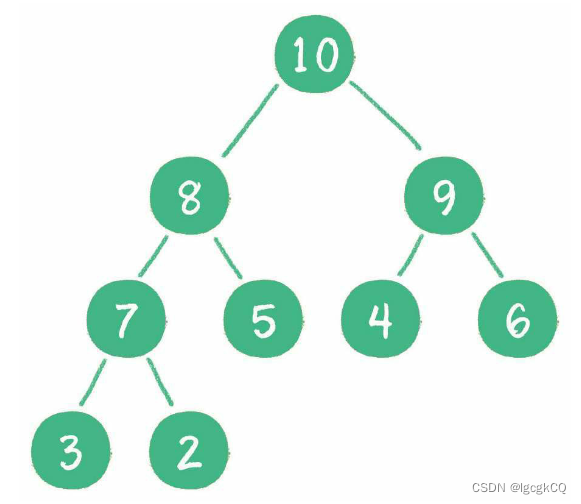
二叉堆本质是一种完全二叉树,分为两个类型:
1.最大堆:任何一个父节点的值,都大于或等于它左、右孩子节点的值
2.最小堆:最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值
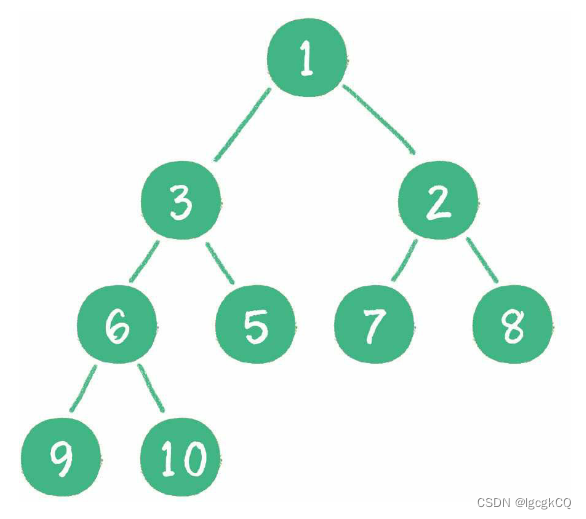
二叉堆的根节点叫作堆顶
特点:
最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素
自我调整
堆的自我调整,就是把一个不符合堆性质的完全二叉树,调整成一个堆;
操作
操作都基于堆的自我调整,以最小堆为例,看一看二叉堆如何进行自我调整
插入加点
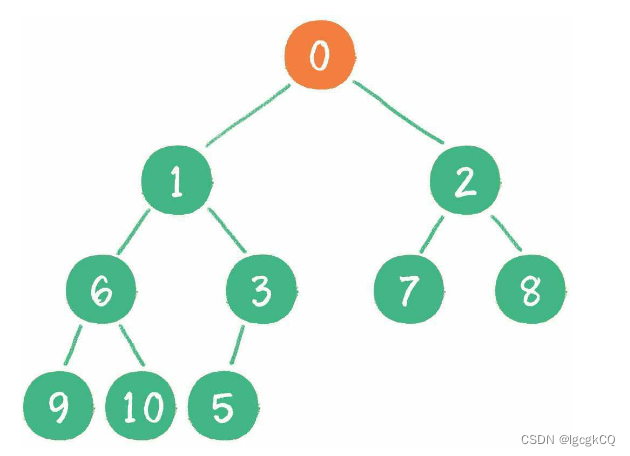
当二叉堆插入节点时,插入位置是完全二叉树的最后一个位置。例如插入一个新节点,值是 0;与父节点进行比较,如果更大,让新节点“上浮”,和父节点交换位置,持续比较,直到0到达堆顶。
删除节点
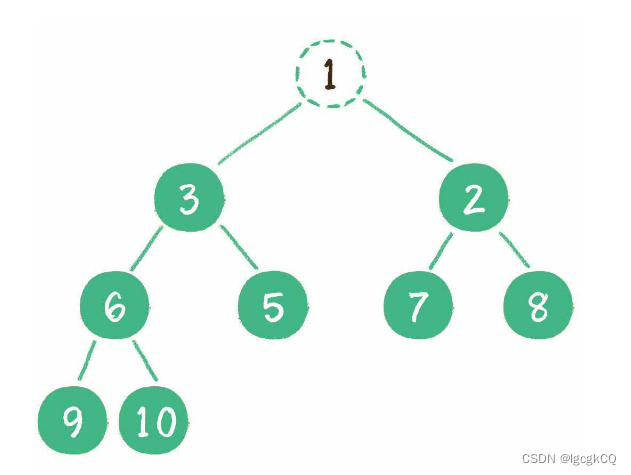
二叉堆删除节点的过程和插入节点的过程正好相反,所删除的是处于堆顶的节点。例如删除最小堆的堆顶节点1;
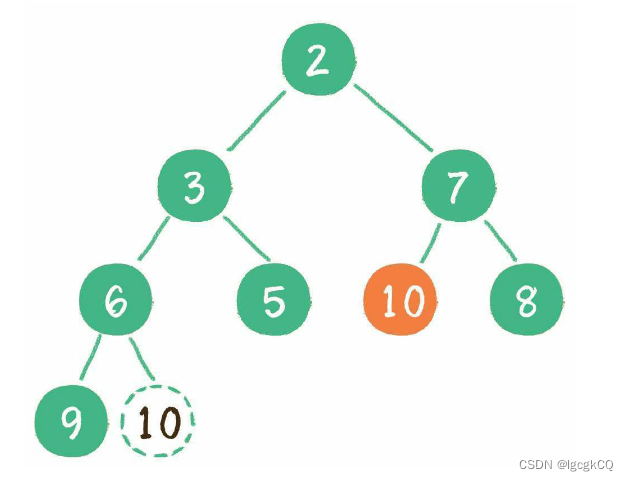
为了继续维持完全二叉树的结构,会把堆的最后一个节点10临时补到原本堆顶的位置;让暂处堆顶位置的节点10和它的左、右孩子进行比较,如果左、右孩子节点中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”,这样一来,二叉堆重新得到了调整
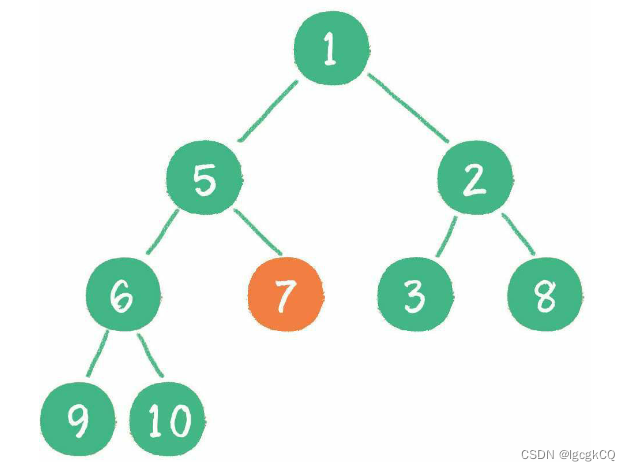
构建二叉堆
构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质就是让所有非叶子节点依次“下沉”
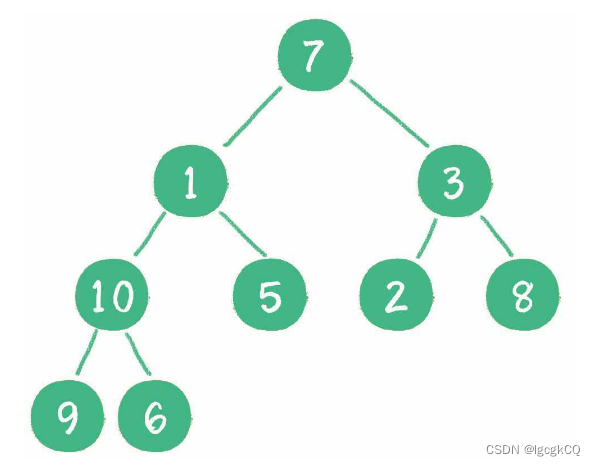
从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左、右孩子节点中最小的一个,则节点10“下沉”
经过上述几轮比较和“下沉”操作,最终每一节点都小于它的左、右孩子节点,一个无序的完全二叉树就被构建成了一个最小堆
代码实现
二叉堆虽然是一个完全二叉树,但它的存储方式并不是链式存储,而是顺序存储。换句话说,二叉堆的所有节点都存储在数组中。

在数组中没有左右指针的情况下,可以依靠数组下标来计算定位一个父节点的左孩子和右孩子:
假设父节点的下标是parent:
左孩子下标: 2×parent+1
右孩子下标: 2×parent+2
1. /**
2. * “上浮”调整
3. * @param array 待调整的堆
4. */
5. public static void upAdjust(int[] array) {
6. int childIndex = array.length-1;
7. int parentIndex = (childIndex-1)/2;
8. // temp 保存插入的叶子节点值,用于最后的赋值
9. int temp = array[childIndex];
10. while (childIndex > 0 && temp < array[parentIndex])
11. {
12. //无须真正交换,单向赋值即可
13. array[childIndex] = array[parentIndex];
14. childIndex = parentIndex;
15. parentIndex = (parentIndex-1) / 2;
16. }
17. array[childIndex] = temp;
18. }
19.
20.
21. /**
22. * “下沉”调整
23. * @param array 待调整的堆
24. * @param parentIndex 要“下沉”的父节点
25. * @param length 堆的有效大小
26. */
27. public static void downAdjust(int[] array, int parentIndex,
int length) {
28. // temp 保存父节点值,用于最后的赋值
29. int temp = array[parentIndex];
30. int childIndex = 2 * parentIndex + 1;
31. while (childIndex < length) {
32. // 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子
33. if (childIndex + 1 < length && array[childIndex + 1] <
array[childIndex]) {
34. childIndex++;
35. }
36. // 如果父节点小于任何一个孩子的值,则直接跳出
37. if (temp <= array[childIndex])
38. break;
39. //无须真正交换,单向赋值即可
40. array[parentIndex] = array[childIndex];
41. parentIndex = childIndex;
42. childIndex = 2 * childIndex + 1;
43. }
44. array[parentIndex] = temp;
45. }
46.
47. /**
48. * 构建堆
49. * @param array 待调整的堆
50. */
51. public static void buildHeap(int[] array) {
52. // 从最后一个非叶子节点开始,依次做“下沉”调整
53. for (int i = (array.length-2)/2; i>=0; i--) {
54. downAdjust(array, i, array.length);
55. }
56. }
57.
58. public static void main(String[] args) {
59. int[] array = new int[] {1,3,2,6,5,7,8,9,10,0};
60. upAdjust(array);
61. System.out.println(Arrays.toString(array));
62.
63. array = new int[] {7,1,3,10,5,2,8,9,6};
64. buildHeap(array);
65. System.out.println(Arrays.toString(array));
66. }优先队列
队列特点:先进先出、后进后出;入队列,将新元素置于队尾,出队列,队头元素最先被移出
特点
最大优先队列,无论入队顺序如何,都是当前最大的元素优先出队
最小优先队列,无论入队顺序如何,都是当前最小的元素优先出队
实现
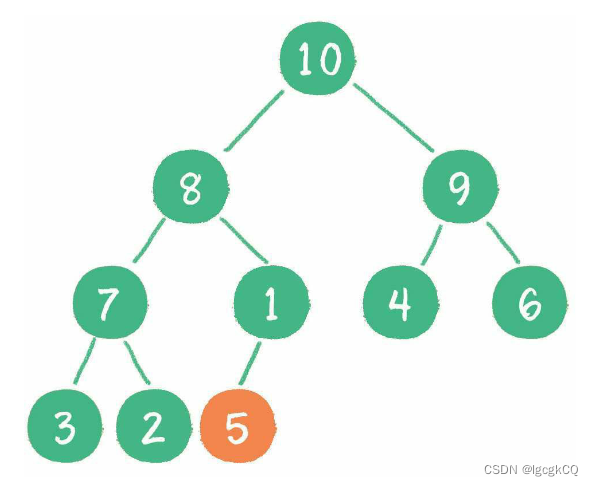
最大堆的堆顶是整个堆中的最大元素,可以用最大堆来实现最大优先队列,这样的话,每一次入队操作就是堆的插入操作,每一次出队操作就是删除堆顶节点
入队操作
1.插入新节点
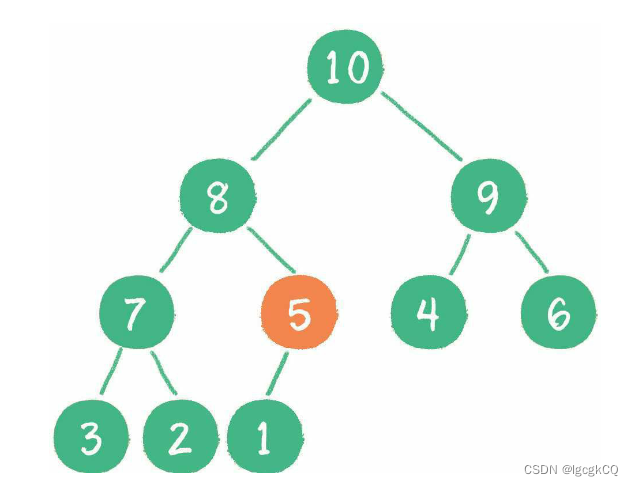
2.新节点上浮到合适位置
出队操作
1.让原堆顶节点10出队
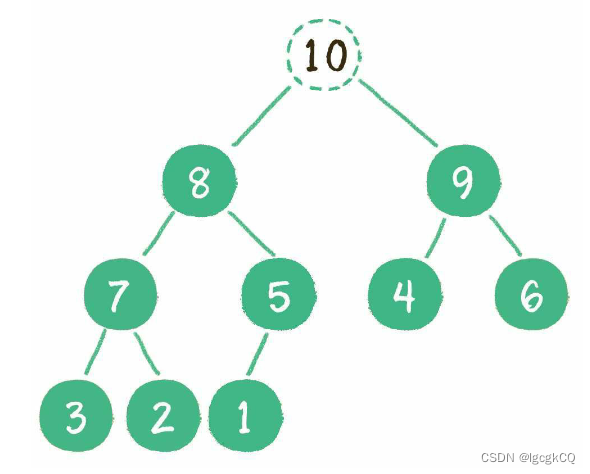
2.把最后一个节点1替换到堆顶位置
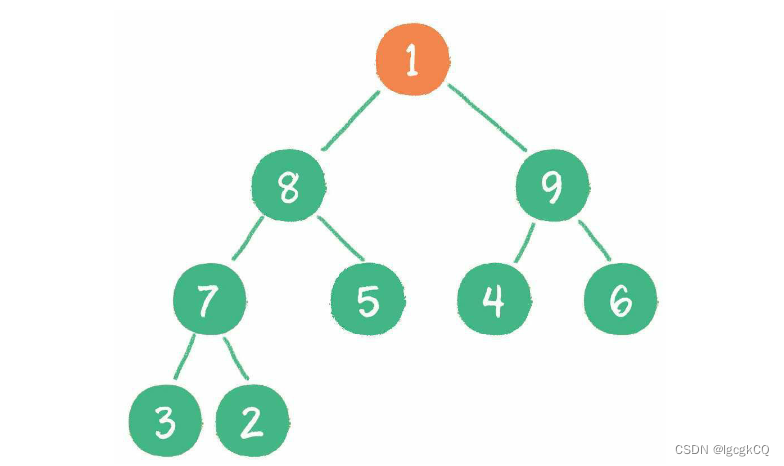
3.节点1“下沉”,节点9成为新堆顶

相关文章:

数据结构与算法:树
目录 树 定义 结构 二叉树 定义 结构 形式 满二叉树 完全二叉树 存储 链式存储结构 数组 孩子节点 父节点 应用 查找 维持相对顺序 遍历 深度优先遍历 前序遍历 中序遍历 后序遍历 广度优先遍历 层序遍历 二叉堆 定义 自我调整 操作 插入加点 删…...
DataFrame的创建、保存与基本操作】)
Spark 【Spark SQL(一)DataFrame的创建、保存与基本操作】
前言 今天学习Spark SQL,前面的RDD编程要想熟练还是得通过项目来熟练,所以先把Spark过一遍,后期针对不足的地方再加强,这样效率会更高一些。 简介 在RDD编程中,我们使用的是SparkContext接口,接下来的Spar…...
026-从零搭建微服务-文件服务(二)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):https://gitee.com/csps/mingyue 源码地址(前端):https://gitee.com/csps…...
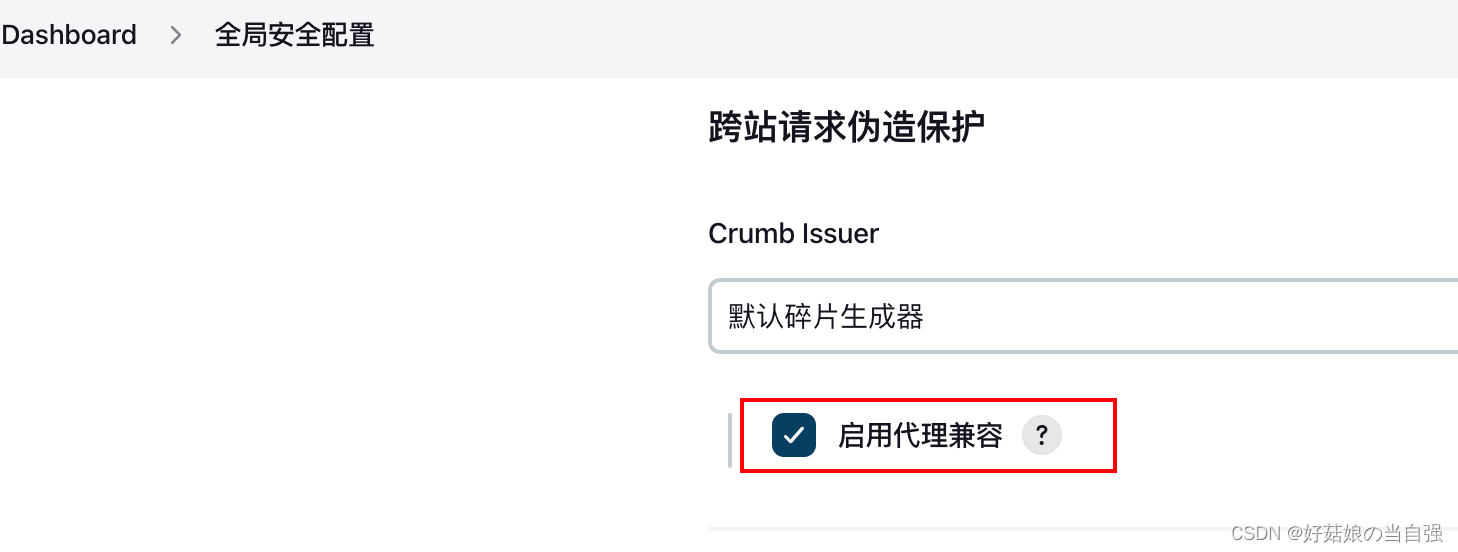
Jenkins 页面部分显示Http状态403 被禁止
前言 生产环境Jenkins部署了一段时间了,结果今天在流水线配置中,部分页面显示Jenkins 页面部分显示Http状态403 被禁止,修改配置点击保存之后偶尔也会出现这个。 问题 以下是问题图片 解决 在全局安全配置里面,勾选上启用代…...
ajax day4
1、promise链式调用 /*** 目标:把回调函数嵌套代码,改成Promise链式调用结构* 需求:获取默认第一个省,第一个市,第一个地区并展示在下拉菜单中*/let pname axios({url: http://hmajax.itheima.net/api/province,}).t…...

8.Spring EL与ExpressionParser
Spring EL与ExpressionParser 文章目录 Spring EL与ExpressionParser介绍**使用SpEL来计算评估文字字符串表达式**使用SpEL来计算评估 bean 属性 – “item.name” 介绍 Spring表达式语言(SpEL)支持多种功能,并且可以测试这个特殊的“ExpressionParser”接口的表达…...

Go和Java实现迭代器模式
Go和Java实现迭代器模式 1、迭代器模式 迭代器模式是 Java 和 .Net 编程环境中非常常用的设计模式。这种模式用于顺序访问集合对象的元素,不需要知道 集合对象的底层表示。 迭代器模式属于行为型模式。 意图:提供一种方法顺序访问一个聚合对象中各个…...

如何在 Vue.js 和 Nuxt.js 之间做出选择?
开篇 今天看了一位国外大佬的文章,主要是他对在项目中如何选择 Vue.js 或 Nuxt.js 的看法,欢迎大家在评论区发表看法,以下内容是他关于这个问题看法的整理,由于翻译水平有限,欢迎大家指正。 国外大佬的看法 Vue.js在开…...

(二十三)大数据实战——Flume数据采集之采集数据聚合案例实战
前言 本节内容我们主要介绍一下Flume数据采集过程中,如何把多个数据采集点的数据聚合到一个地方供分析使用。我们使用hadoop101服务器采集nc数据,hadoop102采集文件数据,将hadoop101和hadoop102服务器采集的数据聚合到hadoop103服务器输出到…...

Linux: network: dhcp: mtu 这个里面也有关于网卡的MTU设置;
https://linux.die.net/man/5/dhcp-options 需注意这个DHCP配置选项。 option interface-mtu uint16; This option specifies the MTU to use on this interface. The minimum legal value for the MTU is 68. 假如在网卡的配置文件中设置了dhcp获取IP信息,可能导…...

Android中使用图片水印,并且能够在线下载字体并应用于水印
Android中使用图片水印,并且能够在线下载字体并应用于水印 要在Android中使用图片水印,并且能够在线下载字体并应用于水印,可以按照以下步骤进行: 1.使用Picasso、Glide或其他图片加载库加载图片: ImageView imageV…...

HTTP文件服务
在工作中,往往会需要将文件同时共享给很多台电脑。 本篇介绍HHDESK的HTTP文件服务功能,通过浏览器,将本地资源共享给任意主机。 1 共享文件 首页——资源管理——服务端——“”,在弹出框中选择HTTP文件服务。 填写各项内容。…...

nginx配置获取客户端的真实ip
场景描述: 访问路径: A机器 - > B机器的 ->C虚拟机 : A机器为客户端用户,本地地址为 192.168.0.110 B机器为服务端反向代理服务器 本地地址为192.168.0.128 –>(192.168.56.1) C机器为B主机安…...

1990-2022上市公司董监高学历工资特征信息数据/上市公司高管信息数据
1990-2022上市公司董监高学历工资特征信息数据/上市公司高管信息数据 1、时间:1990-2022年(统计截止日期为 2022年7月) 2、指标:证券代码、统计截止日期、姓名、国籍、籍贯、籍贯所在地区代码、出生地、出生地所在地区代码、性别…...

Java程序连接 Mysql 超时问题 - 数据包过大,导致超时,# 配置网络超时时间 socketTimeout: 1800000
问题 Java程序连接 Mysql 超时问题 解决方法 如果存在 yml 等类似的配置文件,那么可以配置一下 socket 连接超时的参数,例如 # 配置网络超时时间 半小时,计算公式 60秒*1000毫秒*30分钟 socketTimeout: 1800000...
acwing版)
c++分层最短路(洛谷飞行路线)acwing版
分层最短路算法是在SPFA算法的基础上,将每个点分成若干层,从而使得每个点之间的转移只在同一层次或上下两个相邻层次之间进行,减少了每轮的迭代次数,优化了算法的效率。 #include <iostream> #include <cstdio> #inc…...

Python bs4 BeautifulSoup库使用记录
目录 介绍 安装 初始化 解析器 使用方法 优势 Python标准库 lxml HTML lxml XML html5lib 格式化输出 对象 tag Name 多值属性 其他方法 NavigableString BeautifulSoup Comment 遍历 子节点 父节点 兄弟节点 回退和前进 搜索 过滤器 字符串 正则表达…...
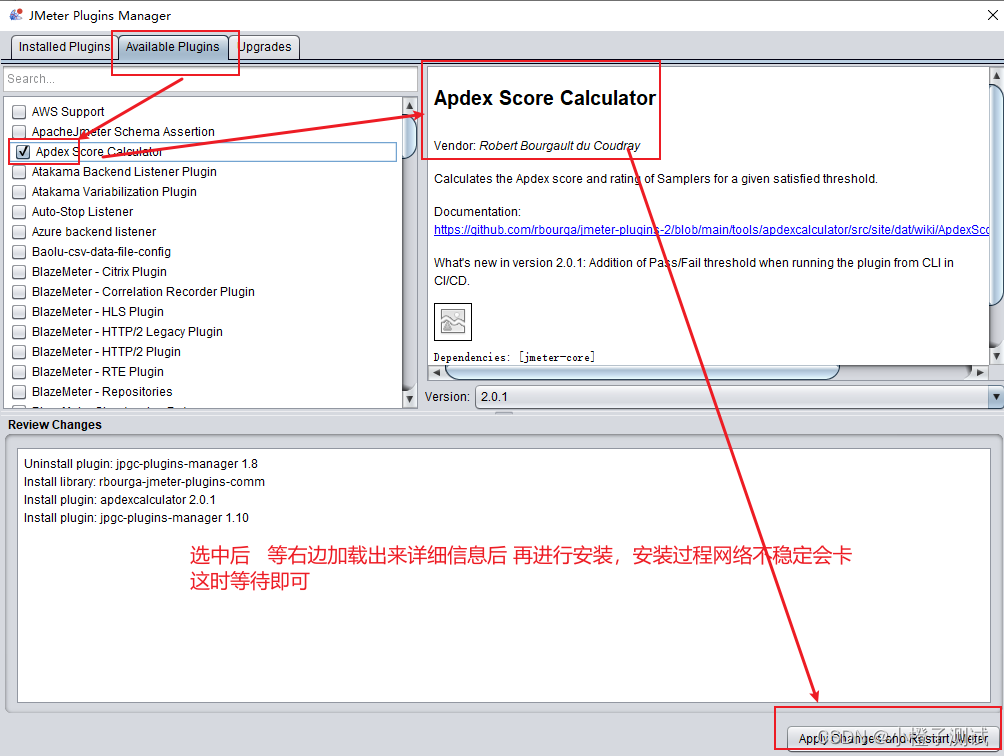
Jmeter系列-插件安装(5)
前言 jmeter4.0以上,如现在最新的5.2.1版本是有集成插件的只需要在官网下载 plugins-manager.jar 包,放在jmeter安装路径的lib/ext目录下即可使用:https://jmeter-plugins.org/install/Install/但并不能满足所有需求,仍然需要安装…...

spring aop源码解析
spring知识回顾 spring的两个重要功能:IOC、AOP,在ioc容器的初始化过程中,会触发2种处理器的调用, 前置处理器(BeanFactoryPostProcessor)后置处理器(BeanPostProcessor)。 前置处理器的调用时机是在容器基本创建完成时ÿ…...
控制物体移动、旋转)
使用Unity的Input.GetAxis(““)控制物体移动、旋转
使用Unity的Input.GetAxis("")控制物体移动、旋转 Input.GetAxis("") 是 Unity 引擎中的一个方法,用于获取游戏玩家在键盘或游戏手柄上输入的某个轴(Axis)的值。这里的 "" 是一个字符串参数,表示要…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
