策略模式,一种广泛应用于各种情况的设计模式(设计模式与开发实践 P5)
文章目录
- 策略模式
- 实现
- 思想
- 实战 - 表单
策略模式
定义:定义一系列算法,把它们一个个封装起来,并且可以互相替换
例如,我们要计算年终奖,年终奖根据绩效 A、B、C 来计算最终数值
实现
最初我们很容易想到用 分支 if 来解决这个问题,如果绩效 = A 则工资 x 2,如果绩效 = B 则工资 x 3
如果经常使用这样的分支结构,你会发现代码耦合度很高,很容易就出现一大坨代码堆砌在一起,只是 x 2 或者 x 3 不足以形成难以维护的结构,但如果不是 x 2 而是一个复杂的代码块,我们显然会想到封装里面的代码!
var performA = function (salary) {return salary * 4;
};var performB = function (salary) {return salary * 3;
};var performC = function (salary) {return salary * 2;
};var calcBonus = function (level, salary) {if (level == "A") {return performA(salary);} else if (level == "B") {return performB(salary);} else if (level == "C") {return performC(salary);}
};是的,虽然我们优化了代码,但没好到哪去,如果要添加一个 D 级,我们还是得堆砌代码
让我们来看看策略模式怎么做吧,策略模式让 策略 被定义和封装,且可以相互替换
这就是最终代码了,但在 javascript 中实现策略相较 C# 或者其他语言来说要容易的多,在下面举例了 C# 代码
var strategies = {A: function (salary) {return salary * 4;},B: function (salary) {return salary * 3;},C: function (salary) {return salary * 2;},
};var calculateBonus = function (level, salary) {return strategies[level](salary);
};
需要注意的是 strategies 对象存储的 3 个匿名函数, Func 类是用来存储函数的,需要一定的函数工具类基础
掌握这样的思想以后,试着把 {"A", (salary) => salary * 4} 解耦出去动态添加即可~
using System;
using System.Collections.Generic;public class Program
{private static Dictionary<string, Func<double, double>> strategies = new Dictionary<string, Func<double, double>>(){{"A", (salary) => salary * 4},{"B", (salary) => salary * 3},{"C", (salary) => salary * 2}};private static double CalculateBonus(string level, double salary){return strategies[level](salary);}public static void Main(string[] args){string level = "A";double salary = 1000;double bonus = CalculateBonus(level, salary);Console.WriteLine("Bonus: " + bonus);}
}
思想
通过上面的重构:
- 消除了大片的分支语句
- 计算奖金的逻辑不再存储在 CalculateBonus 里了,而是分布在策略对象里
- 策略对象只负责计算奖金
- 策略对象之间可以相互替换
实战 - 表单
这是一种尤为常见的表单验证方式,相信绝大多数前端程序员这样写过
显然能发现,这里的 if 堆砌过多,不仅如此,内部的 逻辑 相比上面的代码也更复杂
var registerForm = function (form) {if (form.username.value === "") {alert("用户名不能为空");return false;}if (form.password.value.length < 6) {alert("密码长度不能少于6位");return false;}if (!/(^1[3|5|8][0-9]{9}$)/.test(form.phoneNumber.value)) {alert("手机号码格式不正确");return false;}
};我们可以用策略模式的思路来实现类似这样的代码,这样当我们需要增加验证步骤时,只需要添加策略内容即可:
var validateStrategy = {isNotEmpty: function (form) {if (form.name === "") {return "用户名不能为空";}return "";},minLength: function (form) {if (form.password.length < 6) {return "密码长度不能少于6位";}return "";},isMobile: function (form) {if (!/(^1[3|5|8][0-9]{9}$)/.test(form.phone)) {return "手机号码格式不正确";}return "";},
};var validate = function (form) {for (let func in validateStrategy) {if (validateStrategy.hasOwnProperty(func) &&typeof validateStrategy[func] === "function") {var msg = validateStrategy[func](form);if (msg != "") return false;}}return true;
};相关文章:
)
策略模式,一种广泛应用于各种情况的设计模式(设计模式与开发实践 P5)
文章目录 策略模式实现思想实战 - 表单 策略模式 定义:定义一系列算法,把它们一个个封装起来,并且可以互相替换 例如,我们要计算年终奖,年终奖根据绩效 A、B、C 来计算最终数值 实现 最初我们很容易想到用 分支 if…...

90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。 示例 1: 输入:nums [1,2,2] 输出…...
第四章编程练习题答案)
Intel汇编语言程序设计(第7版)第四章编程练习题答案
1. 大端序转成小端序 .386 .model flat, stdcall option casemap:none include windows.inc include kernel32.inc includelib kernel32.lib include user32.inc includelib user32.lib.stack 4096.data bigEndian BYTE 12h, 34h, 56h, 78h littleEndian DWORD ?Fmt BYTE &…...
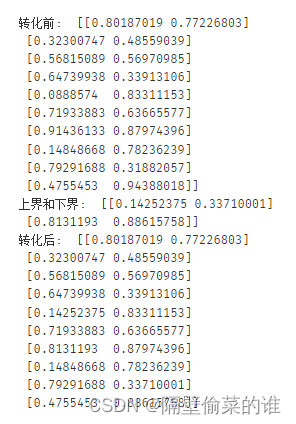
EDA(Exploratory Data Analysis)探索性数据分析
EDA(Exploratory Data Analysis)中文名称为探索性数据分析,是为了在特征工程或模型开发之前对数据有个基本的了解。数据类型通常分为两类:连续类型和离散类型,特征类型不同,我们探索的内容也不同。 1. 特征类型 1.1 连续型特征 …...

Python中的多媒体处理库有哪些?
在Python中,有几个常用的多媒体处理库,包括: Pillow - 一个强大的图像处理库,可以进行图像的读取、保存、剪裁、调整大小、滤镜处理等操作。 OpenCV - 一个用于图像和视频处理的开源计算机视觉库,提供了许多图像处理和…...
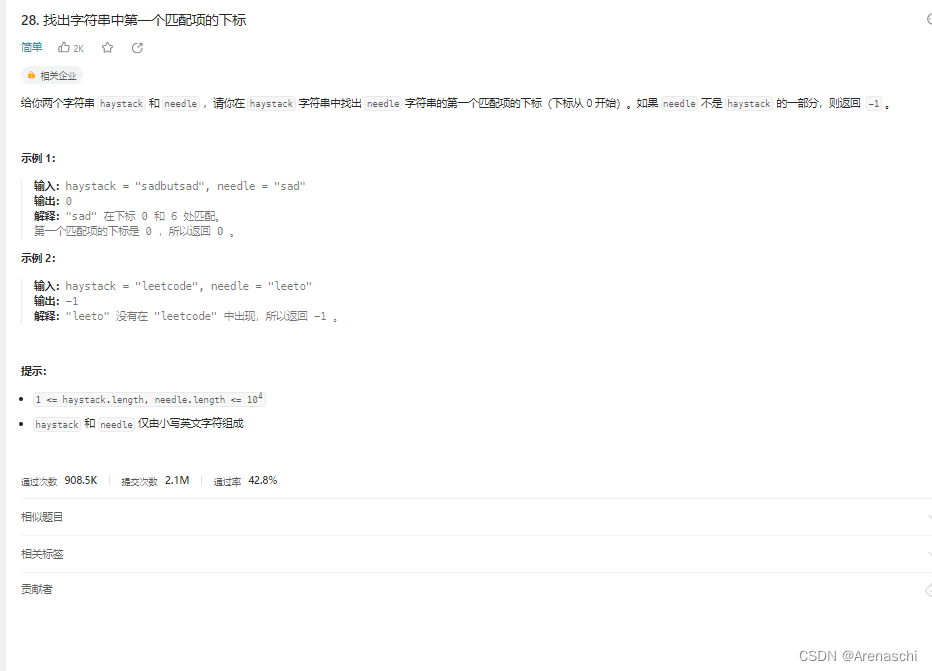
LeetCode【28. 找出字符串中第一个匹配项的下标】
不要用珍宝装饰自己,而要用健康武装身体 给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。 …...

产业互联网开始从简单的概念,逐渐成为可以落地的存在
当流量不再是红利,几乎所有的消费互联网模式开始失效。这一现象,并不仅仅只是体现在流量获取成本的不断增加上,同样还体现在流量激活的难度不断增加上。事实证明,以产业链末端为主要驱动力的发展模式,正在走入到死胡同…...

element-ui tree组件实现在线增删改
这里要实现一个tree 增删改 <!--oracle巡检项--> <template><div class"oracle_instanceType"><el-row type"flex" align"middle" justify"space-between"><iclass"el-icon-s-fold iBox"click&q…...
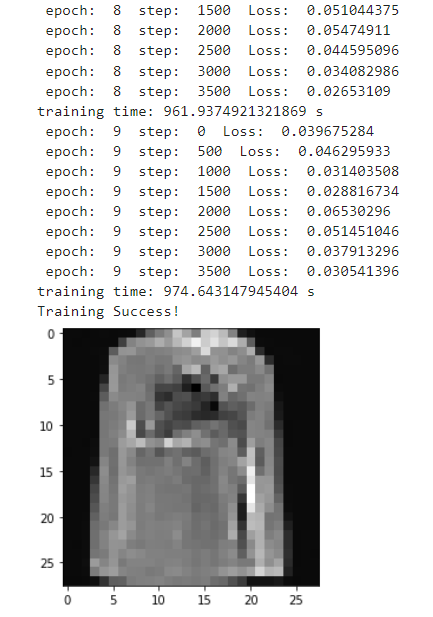
华为开源自研AI框架昇思MindSpore应用案例:消噪的Diffusion扩散模型
目录 一、环境准备1.进入ModelArts官网2.使用CodeLab体验Notebook实例 二、案例实现构建Diffusion模型位置向量ResNet/ConvNeXT块Attention模块组归一化条件U-Net正向扩散数据准备与处理采样训练过程推理过程(从模型中采样) 本文基于Hugging Face&#x…...
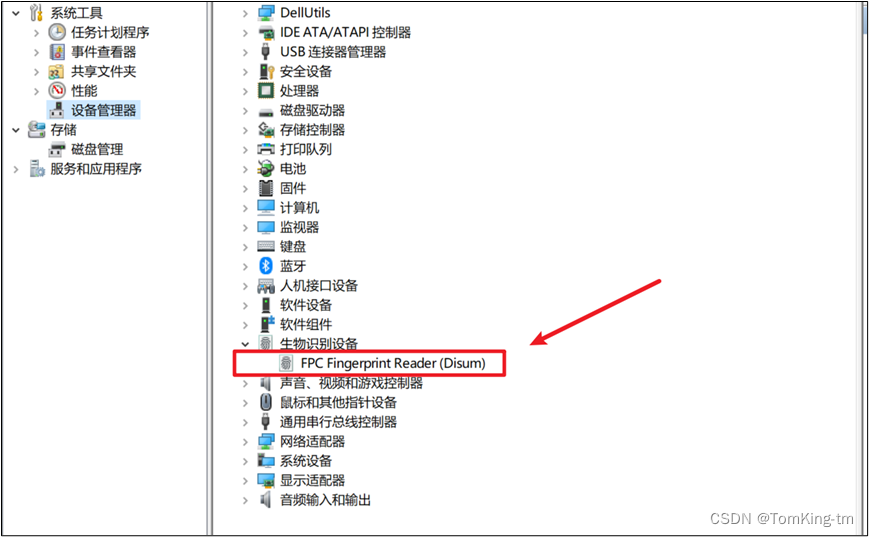
华为CD32键盘使用教程
华为CD32键盘使用教程 用爱发电写的教程! 最后更新时间:2023.9.12 型号:华为有线键盘CD32 基本使用 此键盘在不安装驱动的情况下可以直接使用,但是不安装驱动指纹识别是无法使用的!并且NFC功能只支持华为的部分电脑…...

第三节:在WORD为应用主窗口下关闭EXCEL的操作(2)
【分享成果,随喜正能量】凡事好坏,多半自作自受,既不是神为我们安排,也不是天意偏私袒护。业力之前,机会均等,毫无特殊例外;好坏与否,端看自己是否能应机把握,随缘得度。…...
(04))
Layui + Flask | 弹出层(组件篇)(04)
提示:点击阅读原文体验更佳 https://layui.dev/docs/2.8/layer/ 弹出层组件 layer 是 Layui 最古老的组件,也是使用覆盖面最广泛的代表性组件。在实现网页弹出层的首选交互方案,使用的非常频繁。 打开弹层 layer.open(options); 参数 options : 基础属性配置项。打开弹层的核…...

Electron和vue3集成(推荐仅用于开发)
本篇我们仅实现Electron和vue3通过先运行起vue3项目,再将vue3的url地址交由Electron打开的方案,仅由Electron在vue3项目上套一层壳来达到脱离本机浏览器运行目的 1、参考快速上手 | Vue.js搭建起vue3初始项目 npm install -g vue npm install -g vue/c…...
Vue.js和TypeScript:如何完美结合
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

034:vue项目利用qrcodejs2生成二维码示例
第034个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...
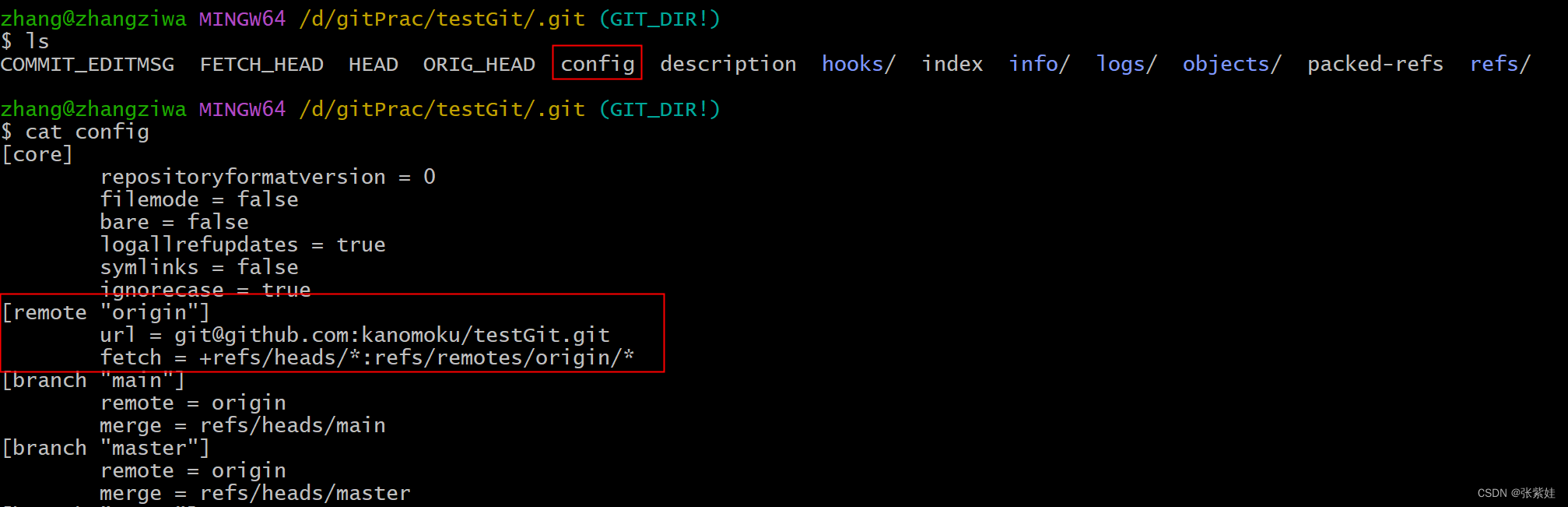
执行 git remote add github git@github.com:xxxx/testGit.git时,git内部做了啥?
git remote add 往 .git/config 中写入了一个叫 [remote "origin"] 配置 url → 表示该远程名称对应的远程仓库地址fetch 参数分为两部分,以冒号 : 进行分割冒号左边 ☞ 本地仓库文件夹冒号右边 ☞ 远程仓库在本地的副本文件夹 ☞ 往里面添加数据的意思 可…...

Makefile基础
迷途小书童 读完需要 4分钟 速读仅需 2 分钟 1 引言 下面这个 C 语言的代码非常简单 #include <stdio.h>int main() {printf("Hello World!.\n");return 0; } 在 Linux 下面,我们使用下面的命令编译就可以 gcc hello.c -o hello 但是随着项目的变大…...

【PickerView案例08-国旗搭建界面加载数据 Objective-C预言】
一、来看我们第三个案例 1.来看我们第三个关于PickerView的一个案例, 首先呢,我要问大家一下, 咱们这个是几组数据呢, 这是一个pickerView,只不过,它显示的是什么,一个界面, 前面两个案例,都是文字 这个案例,开始有图片了, 总结一下这三个案例: 1)第一个案例…...

2023-09-15力扣每日一题
链接: [LCP 50. 宝石补给](https://leetcode.cn/problems/queens-that-can-attack-the-king/) 题意 略 解: 简单题 模拟 实际代码: int giveGem(vector<int>& gem, vector<vector<int>>& operations) {for(…...
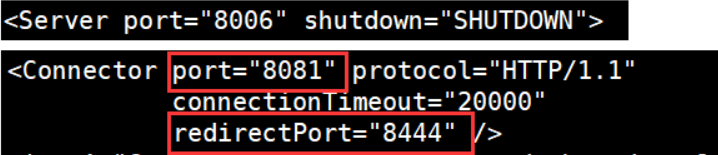
系列七、Nginx负载均衡配置
一、目标 浏览器中访问http://{IP地址}:9002/edu/index.html,浏览器交替打印清华大学8080、清华大学8081. 二、步骤 2.1、在tomcat8080、tomcat8081的webapps中分别创建edu文件夹 2.2、将index.html分别上传至edu文件夹 注意事项:tomcat8080的edu文件…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...
