基于matlab实现的平面波展开法二维声子晶体能带计算程序
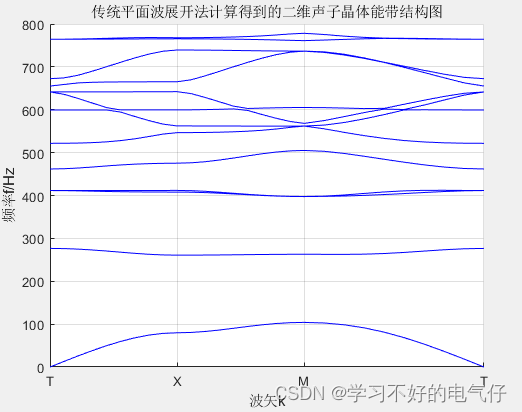
Matlab 平面波展开法计算二维声子晶体二维声子晶体带结构计算,材料是铅柱在橡胶基体中周期排列,格子为正方形。采用PWE方法计算
完整程序:
%%%%%%%%%%%%%%%%%%%%%%%%%
clear;clc;tic;epssys=1.0e-6; %设定一个最小量,避免系统截断误差或除零错误
%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义实际的正空间格子基矢
%%%%%%%%%%%%%%%%%%%%%%%%%%
a=0.02;
a1=a*[1 0];
a2=a*[0 1];
%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义晶格的参数
%%%%%%%%%%%%%%%%%%%%%%%%%%
rho1=11600;E1=4.08e10;mju1=1.49e10;lambda1=mju1*(E1-2*mju1)/(3*mju1-E1); %散射体的材料参数
rho2=1300;E2=1.175e5;mju2=4e4;lambda2=mju2*(E2-2*mju2)/(3*mju2-E2); %基体的材料参数
Rc=0.006; %散射体截面半径
Ac=pi*(Rc)^2; %散射体截面面积
Au=a^2; %二维格子原胞面积
Pf=Ac/Au; %填充率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成倒格基矢
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
b1=2*pi/a*[1 0];
b2=2*pi/a*[0 1];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%选定参与运算的倒空间格矢量,即参与运算的平面波数量
%设定一个l,m的取值范围,变化l,m即可得出参与运算的平面波集合
NrSquare=10; %选定倒空间的尺度,即l,m(倒格矢G=l*b1+m*b2)的取值范围。
%NrSquare确定后,使用Bloch波数目可能为(2*NrSquare+1)^2
G=zeros((2*NrSquare+1)^2,2); %初始化可能使用的倒格矢矩阵
i=1;
for l=-NrSquare:NrSquare
for m=-NrSquare:NrSquare
G(i,:)=l*b1+m*b2;
i=i+1;
end;
end;
NG=i-1; %实际使用的Bloch波数目
G=G(1:NG,:);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成k空间的rho(Gi-Gj),mju(Gi-Gj),lambda(Gi-Gj)值,i,j从1到NG。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rho=zeros(NG,NG);mju=zeros(NG,NG);lambda=zeros(NG,NG);
for i=1:NG
for j=1:NG
Gij=norm(G(j,:)-G(i,:));
if (Gij<epssys)
rho(i,j)=rho1*Pf+rho2*(1-Pf);
mju(i,j)=mju1*Pf+mju2*(1-Pf);
lambda(i,j)=lambda1*Pf+lambda2*(1-Pf);
else
rho(i,j)=(rho1-rho2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
mju(i,j)=(mju1-mju2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
lambda(i,j)=(lambda1-lambda2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
end;
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义简约布里渊区的各高对称点
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
T=(2*pi/a)*[epssys 0];
M=(2*pi/a)*[1/2 1/2];
X=(2*pi/a)*[1/2 0];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于简约布里渊区边界上的每个k,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
THETA_A=zeros(NG,NG); %待解的本征方程A矩阵
THETA_B=zeros(NG,NG); %待解的本征方程B矩阵
Nkpoints=10; %每个方向上取的点数
stepsize=0:1/(Nkpoints-1):1; %每个方向上步长
TX_eig=zeros(Nkpoints,NG); %沿TX方向的波的待解的特征频率矩阵
XM_eig=zeros(Nkpoints,NG); %沿XM方向的波的待解的特征频率矩阵
MT_eig=zeros(Nkpoints,NG); %沿MT方向的波的待解的特征频率矩阵
for n=1:Nkpoints
fprintf(['\n k-point:',int2str(n),'of',int2str(Nkpoints),'.\n']);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于TX(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
TX_step=stepsize(n)*(X-T)+T;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=TX_step+G(i,:);
kGj=TX_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解TX(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
TX_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于XM(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XM_step=stepsize(n)*(M-X)+X;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=XM_step+G(i,:);
kGj=XM_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解XM(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XM_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于MT(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MT_step=stepsize(n)*(T-M)+M;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=MT_step+G(i,:);
kGj=MT_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解MT(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MT_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
end;
fprintf('\n Calculation Time:%d sec',toc);
save pbs2D
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%绘制声子晶体能带结构图
%首先将特定方向(正方格子:TX,XM,MT)离散化
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
kaxis=0;
TXaxis=kaxis:norm(T-X)/(Nkpoints-1):(kaxis+norm(T-X));
kaxis=kaxis+norm(T-X);
XMaxis=kaxis:norm(M-X)/(Nkpoints-1):(kaxis+norm(X-M));
kaxis=kaxis+norm(X-M);
MTaxis=kaxis:norm(T-M)/(Nkpoints-1):(kaxis+norm(T-M));
kaxis=kaxis+norm(T-M);
Ntraject=3; %所需绘制的特定方向的数目
EigFreq=zeros(Ntraject*Nkpoints,1);
figure(1)
hold on;
Nk=Nkpoints;
for k=1:NG
for i=1:Nkpoints
EigFreq(i+0*Nk)=TX_eig(i,k)/(2*pi);
EigFreq(i+1*Nk)=XM_eig(i,k)/(2*pi);
EigFreq(i+2*Nk)=MT_eig(i,k)/(2*pi);
end;
plot(TXaxis(1:Nk),EigFreq(1+0*Nk:1*Nk),'b',...
XMaxis(1:Nk),EigFreq(1+1*Nk:2*Nk),'b',...
MTaxis(1:Nk),EigFreq(1+2*Nk:3*Nk),'b');
end;
grid on;
hold off;
titlestr='传统平面波展开法计算得到的二维声子晶体能带结构图';
title(titlestr);
xlabel('波矢k');
ylabel('频率f/Hz');
axis([0 MTaxis(Nkpoints) 0 800]);
set(gca,'XTick',[TXaxis(1) TXaxis(Nkpoints) XMaxis(Nkpoints) MTaxis(Nkpoints)]);
xtixlabel=char('T','X','M','T');
set(gca,'XTickLabel',xtixlabel);
相关文章:

基于matlab实现的平面波展开法二维声子晶体能带计算程序
Matlab 平面波展开法计算二维声子晶体二维声子晶体带结构计算,材料是铅柱在橡胶基体中周期排列,格子为正方形。采用PWE方法计算 完整程序: %%%%%%%%%%%%%%%%%%%%%%%%% clear;clc;tic;epssys1.0e-6; %设定一个最小量,避免系统截断误差或除零错…...
Minio入门系列【2】纠删码
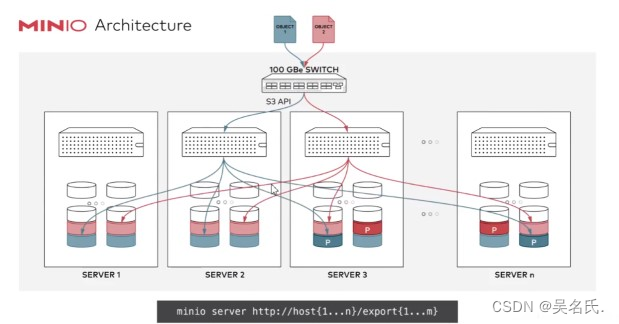
1 纠删码 Minio使用纠删码erasure code和校验和checksum来保护数据免受硬件故障和无声数据损坏。 即便丢失一半数量(N/2)的硬盘,仍然可以恢复数据 1.1 什么叫纠删码 纠删码是一种用于重建丢失或损坏数据的数学算法。 纠删码(e…...
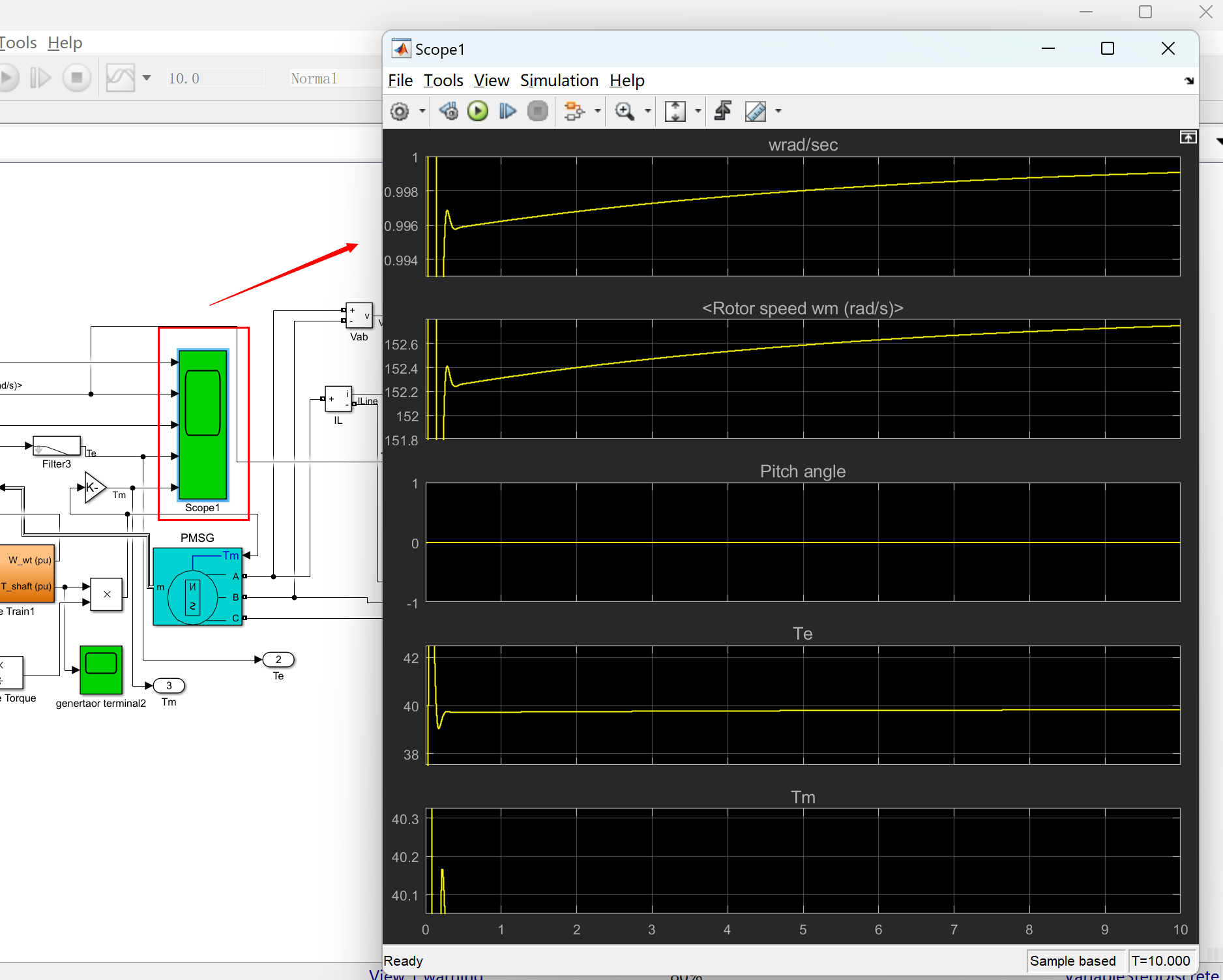
基于永磁同步发电机的风力发电系统研究(Simulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
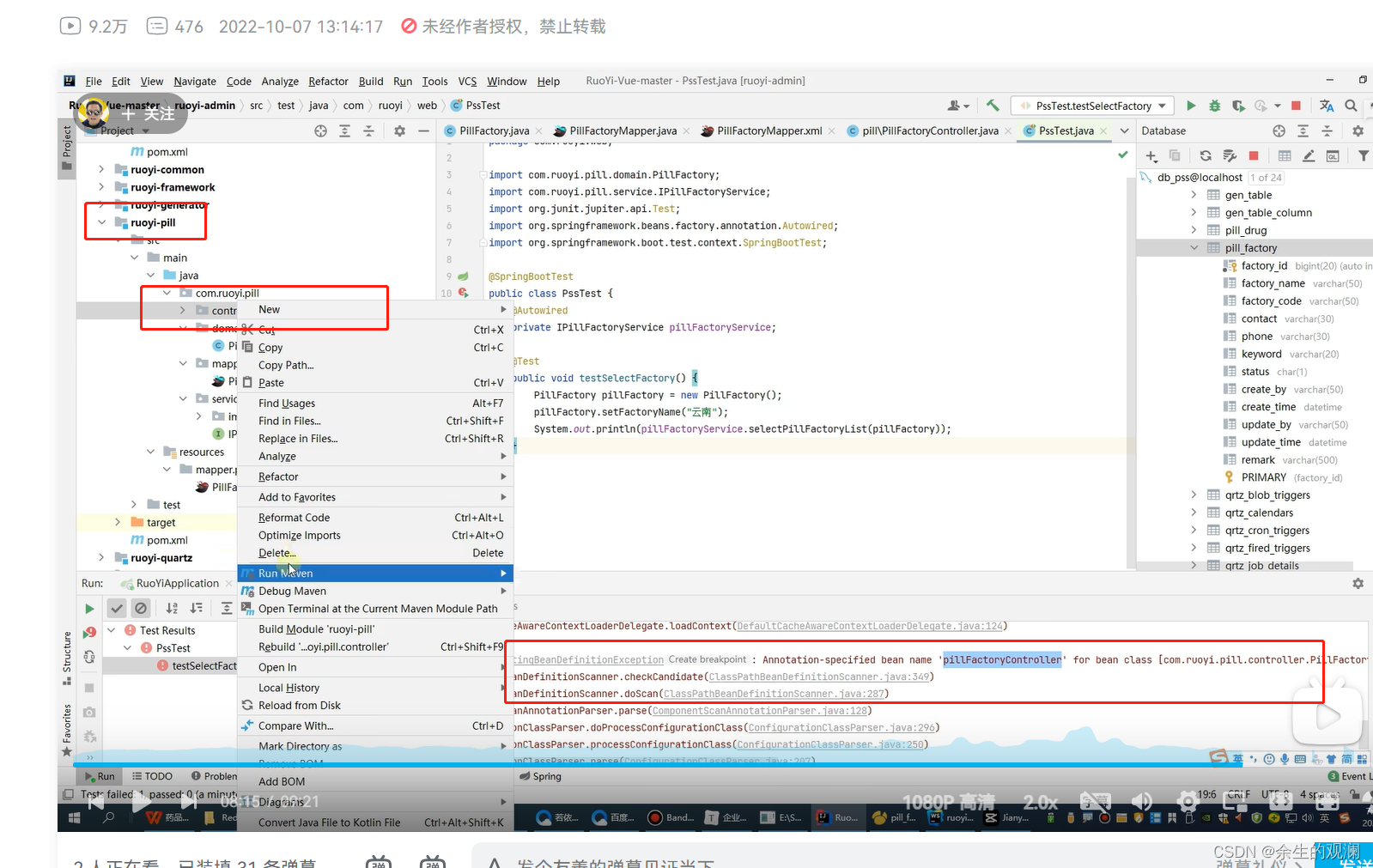
5.后端·新建子模块与开发(自动模式)
文章目录 学习资料自动生成模式创建后端三层 学习资料 https://www.bilibili.com/video/BV13g411Y7GS?p11&spm_id_frompageDriver&vd_sourceed09a620bf87401694f763818a31c91e 自动生成模式创建后端三层 首先,运行起来若依的前后端整个项目,…...
这样而不是data:{}这样?)
vue的data为什么要写成data(return{})这样而不是data:{}这样?
在Vue.js中,为什么要将data写成一个返回对象的函数data()而不是一个普通的对象data: {} 为什么? 因为Vue.js的组件实例是可复用的,而且它们可以在应用中多次实例化。通过将data定义为一个返回对象的函数,可以确保每个组件实例都…...

MySQL基础运维知识点大全
一. MySQL基本知识 1. 目录的功能 通用 Unix/Linux 二进制包的 MySQL 安装下目录的相关功能 目录目录目录binMySQLd服务器,客户端和实用程序docs信息格式的 MySQL 手册manUnix 手册页include包括(头)文件lib图书馆share用于数据库安装的错…...

javascript获取样式表的规则及读取与写入
CSSStyleSheet是继承了StyleSheet的接口属性,它是用于找当前文档中的<link rel“” href“”…>这样文件的,有以下属性:lenght,cssRules,title,href,type,deleteRule,insertRule等 CSSStyleRule是继承于CSSRule,它是用于找<link re…...

什么是promise?
是JavaScript中用于处理异步操作的一种机制。 异步操作,例如从服务器获取数据、读取文件、执行数据库查询等等。 经典使用:Axios 是一个基于Promise的HTTP客户端 Promise具有三个状态: Pending(待定):Pr…...

从零开始学习软件测试-第45天笔记
monkey事件 事件:对app进行的操作,比如触摸事件,滑动事件...动作:构成一个事件所需要的步骤。 调整事件的百分比 adb shell monkey -p 包名 -v -v --pct-xxx 百分比 次数>输出文件的路径 分析日志有没有报错 到日志中去找…...

visual studio常用快捷键
CtrlM、CtrlO 折叠到定义 CtrlM、CtrlM 折叠当前定义 CtrlM、CtrlA 折叠全部 CtrlK、CtrlD 自动编排代码格式 F12 转到定义 ShiftF12 查看所有定义 ctrl] 转到定义首部或尾部 ctrlX 未选中文本时,剪切/删除光标所在行。ctrlV 未选中文本时,粘贴到…...

数据变换:数据挖掘的准备工作之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Go语言实践案例之简单字典
一、程序要实现效果: 在命令行调用程序的时候,可以在命令行的后面查询一个单词,然后会输出单词的音标和注释。 二、思路分析: 定义一个结构体 DictRequest,用于表示翻译请求的数据结构。其中包含了 TransType&#…...
)
笔试面试相关记录(3)
(1)String String和String.append()的底层实现 C中string append函数的使用与字符串拼接「建议收藏」-腾讯云开发者社区-腾讯云 (tencent.com) String String 在 第二个String中遇到\0就截止,append()的方法则是所有字符都会加在后面。 &…...
第6章_瑞萨MCU零基础入门系列教程之串行通信接口(SCI)
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

开源免费的流程图软件draw.io
2023年9月16日,周六上午 想买微软的visio,但发现不是很值得,因为我平时也不是经常需要画图。 所以我最后还是决定使用开源免费的draw.io来画图 draw.io网页版的网址: Flowchart Maker & Online Diagram Software draw.io的…...
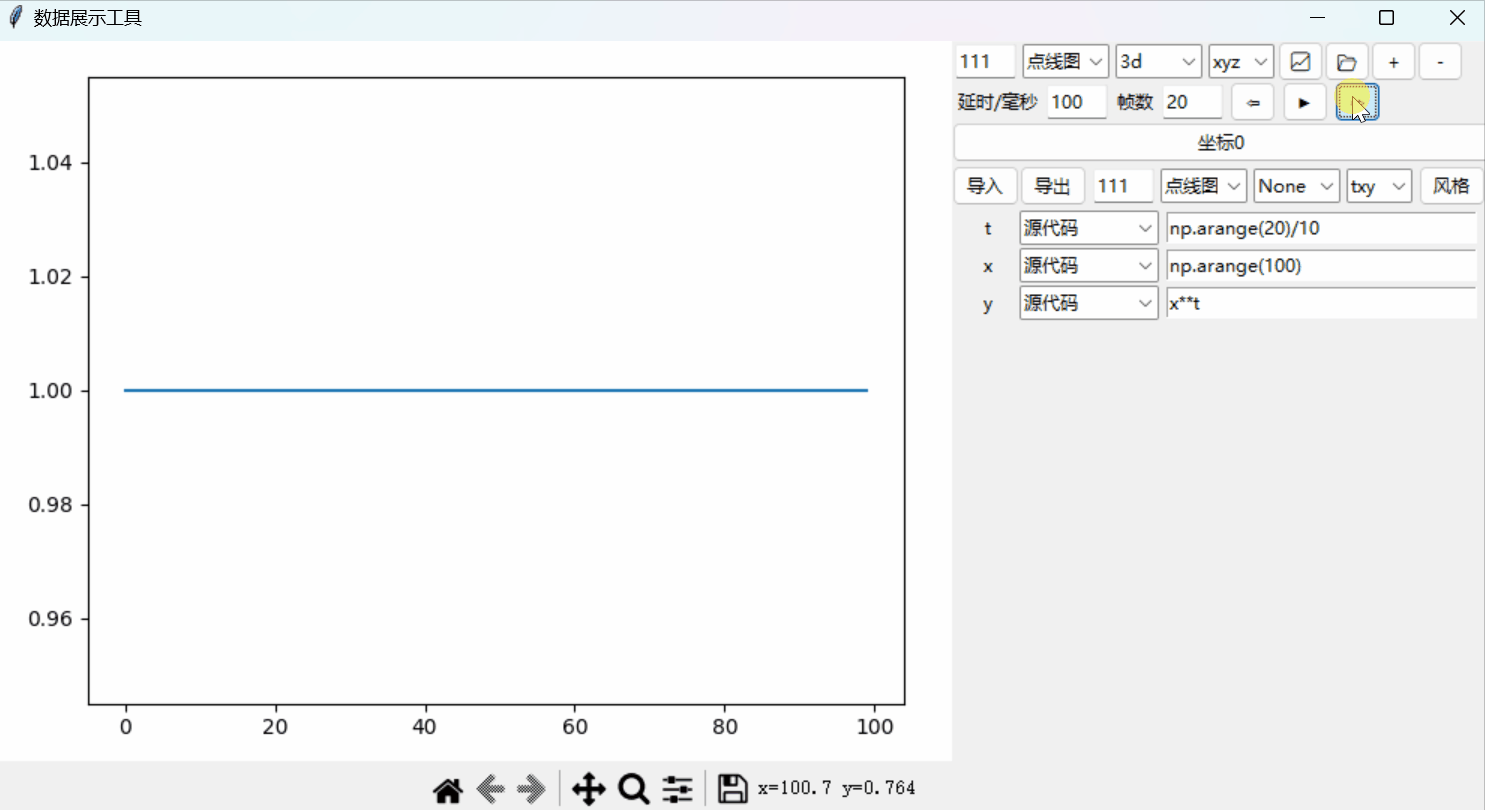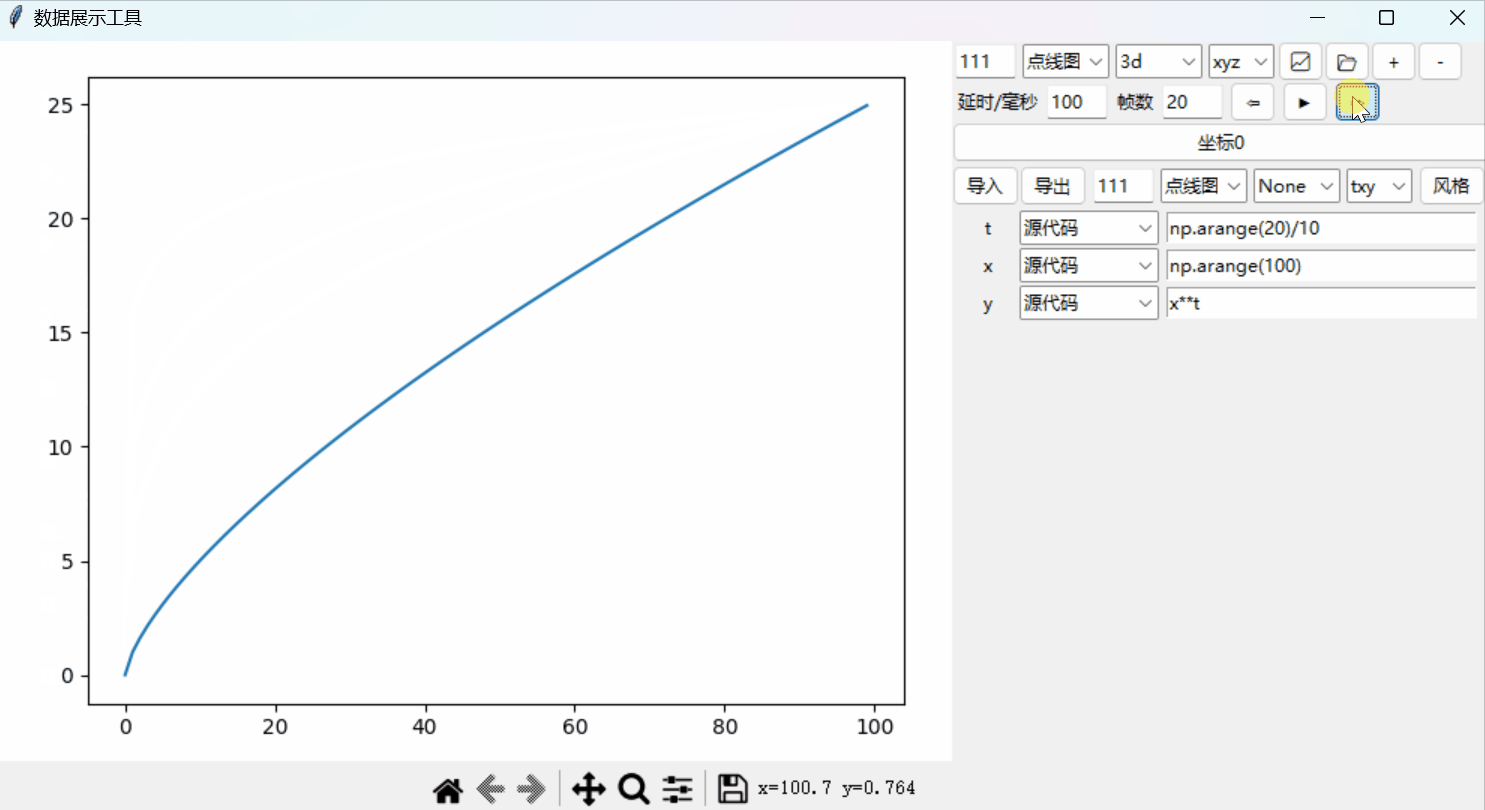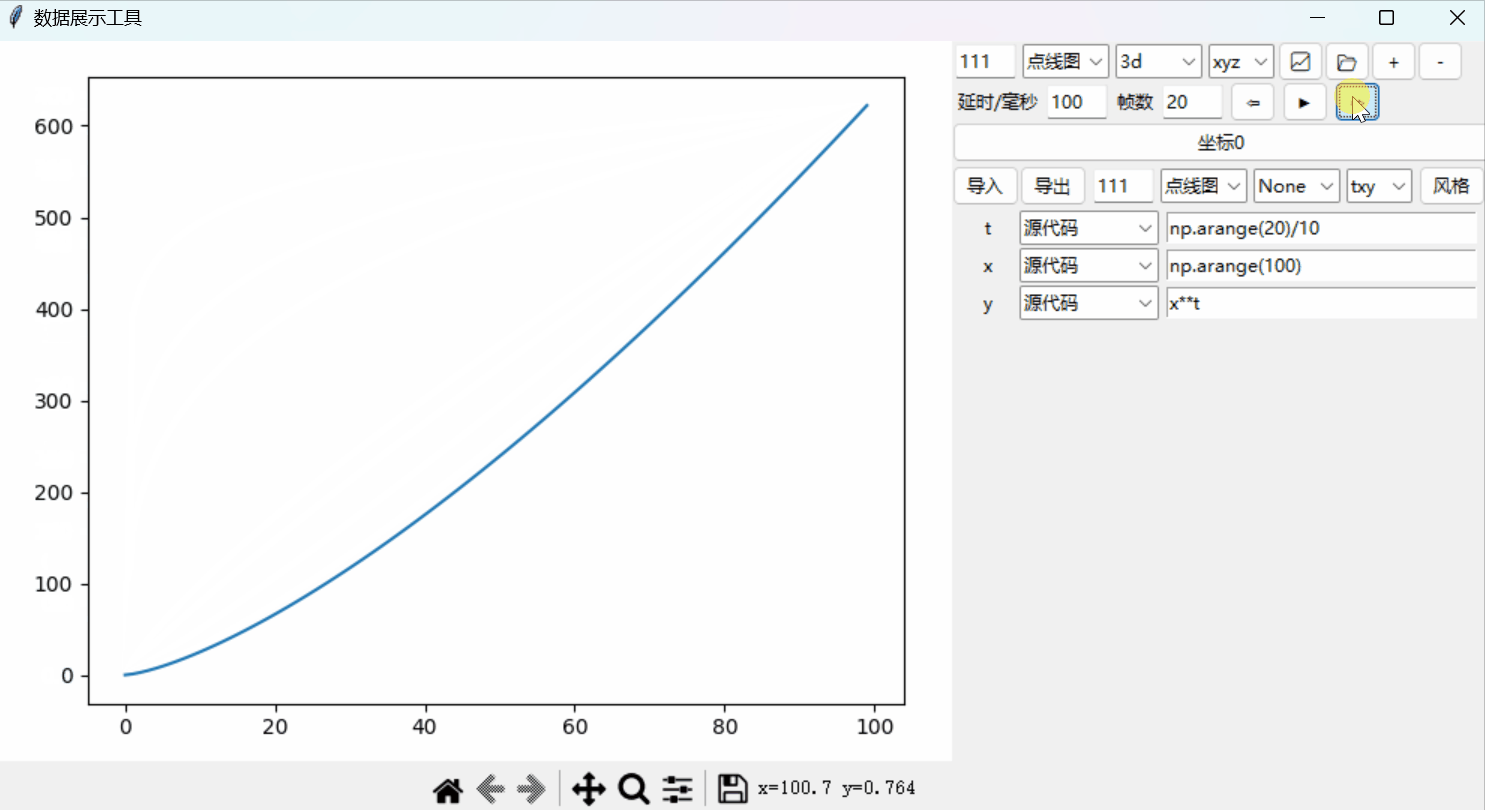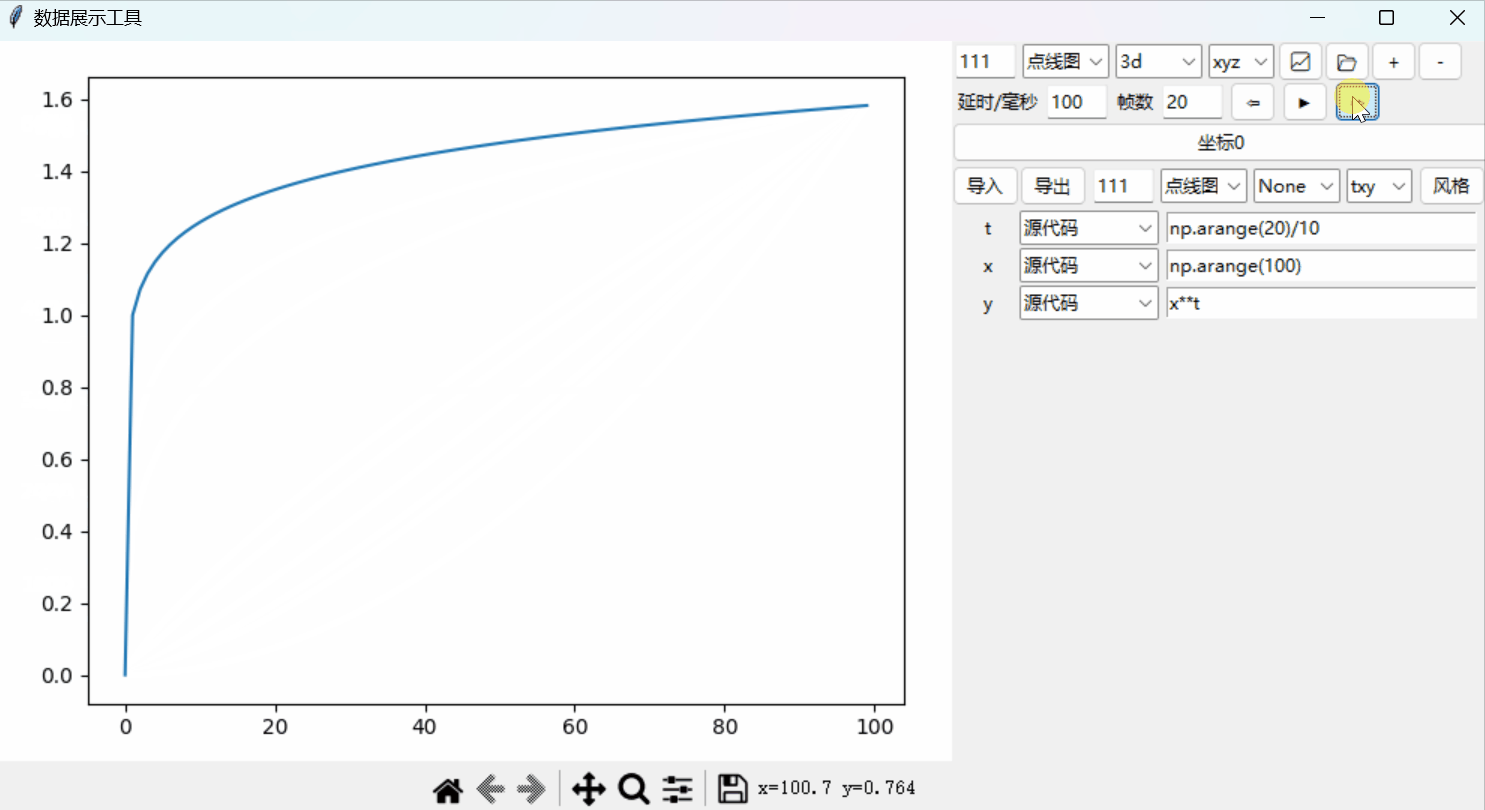
Python绘图系统19:添加时间轴以实现动态绘图
文章目录 时间轴单帧跳转源代码 Python绘图系统: 📈从0开始的3D绘图系统📉一套3D坐标,多个函数📊散点图、极坐标和子图自定义控件:绘图风格📉风格控件📊定制绘图风格坐标设置进阶&a…...
深度解析shell脚本的命令的原理之rm
rm 是 Unix/Linux 系统中的一个基本命令,用于删除文件或目录。以下是对这个命令的深度分析: 基本操作:rm 命令删除一个或多个文件或目录。这是通过从文件系统中移除链接来完成的。在 Unix/Linux 中,文件是通过链接(可以…...
)
RPA机器人流程自动化专题培训大纲(供大家参考使用)
一、RPA机器人流程自动化概述 RPA的定义和发展历程RPA的应用场景和优势RPA与人工智能的关系 二、RPA机器人流程自动化基础知识 RPA的基本原理和技术架构RPA的常用技术和工具RPA的编程语言和开发环境 三、RPA机器人流程自动化实战应用 如何进行业务流程分析与优化如何利用R…...
Python用若干列的数据多条件筛选、去除Excel数据并批量绘制直方图
本文介绍基于Python,读取Excel数据,以一列数据的值为标准,对这一列数据处于指定范围的所有行,再用其他几列数据数值,加以筛选与剔除;同时,对筛选与剔除前、后的数据分别绘制若干直方图ÿ…...
驱动开发,IO多路复用实现过程,epoll方式
1.框架图 被称为当前时代最好用的io多路复用方式; 核心操作:一棵树(红黑树)、一张表(内核链表)以及三个接口; 思想:(fd代表文件描述符) epoll要把检测的事件…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
