算法通关村-----动态规划高频问题
最少硬币数问题
问题描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。详见leetcode322
问题分析
设f(n)为amount=n时使用的最少金币数。遍历coins数组,选择f(n-coins[i])(i=0,1,coins.length-1)的最小值,即为需要的最少硬币数,递归继续寻找f(n-coins[i])的最小值,初始时f(0)=0,如果一些总金额无法凑成时,可以使用amount+1填充数组。
代码实现
public int coinChange(int[] coins, int amount) {int[] res = new int[amount+1];int max = amount+1;Arrays.fill(res,max);res[0] = 0;int[] temp = new int[coins.length];for(int i=1;i<amount+1;i++){for(int j=0;j<coins.length;j++){int leftAmount = i - coins[j];temp[j] = leftAmount>=0?res[leftAmount]+1:max;}int min = max;for(int j=0;j<coins.length;j++){min = Math.min(temp[j],min);}res[i]= min;}if(res[amount]==max){return -1;}return res[amount];
}
最长连续递增子序列
问题描述
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。详见leetcode674
问题分析
这道题,我们之前使用滑动窗口的方式也可以解决,使用动态规划解题时,对于连续递增子序列的最后一个元素nums[k],存在两种情况,第一种是最长连续递增子序列长度为1,连续递增子序列只包含一个元素nums[k],第二种是存在k-1,使得nums[k-1]<num[k],设f[k]为到下标k处的连续递增子序列长度,则,如果nums[k-1]>=nums[k],f[k]=1,否则f[k]=f[k-1]+1,初始值f[0]=1,
代码实现
滑动窗口实现
public int findLengthOfLCIS(int[] nums) { if(nums.length==0||nums.length==1){return nums.length;}int res = 1;int count =1;for(int i=1;i<nums.length;i++){if(nums[i-1]>=nums[i]){count =1;}else{count++;}if(count>res){res = count;}}return res;
}
动态规划实现
public int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];Arrays.fill(dp,1);int max = 1;for(int i=1;i<nums.length;i++){if(nums[i]>nums[i-1]){dp[i] = dp[i-1]+1;max = Math.max(dp[i],max);}}return max;
}
最长递增子序列
问题描述
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。详见leetcode300
问题分析
这道题与上一题相似,只是不需要连续递增。对于最长递增子序列的最后一个元素nums[k],存在两种情况,第一种是最长连续递增子序列长度为1,连续递增子序列只包含一个元素nums[k],第二种是存在i,使得i<k,nums[i]<num[k],设f[k]为到下标k处的连续递增子序列长度,则f[k] = max{f[i]+1}(i是所有nums[i]<nums[k]的集合)
代码实现
public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];Arrays.fill(dp,1);for(int i=1;i<nums.length;i++){for(int j=i-1;j>=0;j--){if(nums[j]<nums[i]&&dp[j]+1>dp[i]){dp[i] = dp[j]+1;}}}int max = 1;for(int i=0;i<nums.length;i++){max = Math.max(max,dp[i]);}return max;
}
最少完全平方数
问题描述
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。详见leetcode279
问题分析
设f(n)表示和为 n 的完全平方数的最少数量 。则f(n)=min{f(n-jj)+1}(j是满足所有jj<=n的j的集合).初始时f(0) = 0.
代码实现
public int numSquares(int n) {int[] f = new int[n+1];Arrays.fill(f,Integer.MAX_VALUE);f[0] = 0;for(int i=1;i<n+1;i++){for(int j=1;j*j<=i;j++){if(f[i-j*j]+1<f[i]){f[i] = f[i-j*j]+1;}}}return f[n];
}
跳跃游戏
问题描述
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。详见leetcode55
问题分析
设f(n)是一个boolean数组,为true表示可以跳到数组下标n处,为false表示无法跳到数组下标n处。f(n)为true的条件是f(i)为true,n-1-i<nums[i],初始时f(0)=true
public boolean canJump(int[] nums) {boolean[] f = new boolean[nums.length];Arrays.fill(f,false);f[0] = true;for(int i=1;i<nums.length;i++){for(int j=0;j<i;j++){if(f[j]&&j+nums[j]>=i){f[i] = true;break;}}} return f[nums.length-1];
}
总结
这部分动态规划问题需要我们你想推导,即如何由我们想要结果的前一个状态得到我们想要的结果(往往是最值,所以涉及从前面多个状态到当前状态的选择)。逆向推导得到状态转移方程f,确定初始条件,一步步填充dp数组,最终得到我们想要的结果并返回。
相关文章:

算法通关村-----动态规划高频问题
最少硬币数问题 问题描述 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬…...

记一起小意外事件引起的批量重命名文件名
一、事件描述 某次,因某业务系统迁移,一线人员对业务目录误操作,执行打包命令过程中导致Tomcat下的web应用程序无法使用,检查后发现项目下所有文件名都加了gz格式;询问一线,发现是对项目目录执行了:gzip -r ./tomcat导致程序文件找不到;报错如下: 二、事件处理 1、查看…...

【Excel函数】Excel的Len函数求对象的字符数
在Excel中,LEN函数用于计算文本字符串中的字符数。它的语法如下。 LEN(text) 其中,text是要计算字符数的文本字符串。 例如,如果你想计算单元格A1中文本的字符数,可以使用以下公式: A2len(a1) 结果将返回单元格A1中文…...
小白备战大厂算法笔试(八)——搜索
搜索 二分查找 二分查找是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮减少一半搜索范围,直至找到目标元素或搜索区间为空为止。 Question: 给定一个长度为n的数组 nums ,元素按从小到大的顺序排列,数组…...

〔022〕Stable Diffusion 之 生成视频 篇
✨ 目录 🎈 视频转换 / mov2mov🎈 视频转换前奏准备🎈 视频转换 mov2mov 使用🎈 视频转换 mov2mov 效果预览🎈 视频无限缩放 / Infinite Zoom🎈 视频无限缩放 Infinite Zoom 使用 🎈 视频转换 /…...
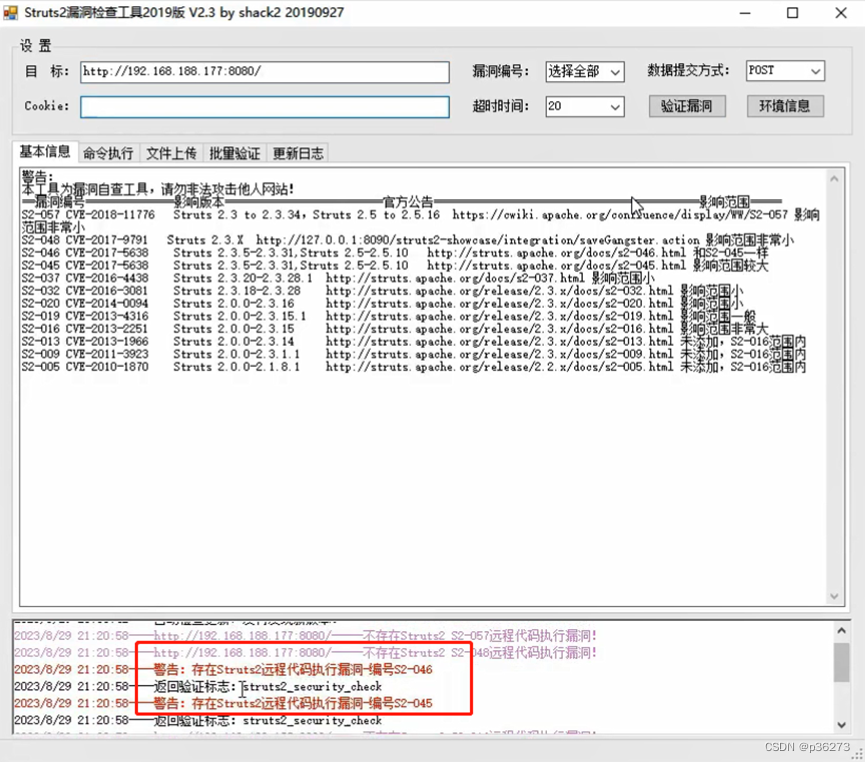
网络安全深入学习第三课——热门框架漏洞(RCE—Struts2远程代码执行)
文章目录 一、Struts2框架介绍二、Struts2远程代码执行漏洞三、Struts2执行代码的原理四、Struts2框架特征五、漏洞手工POC六、漏洞工具复现 一、Struts2框架介绍 ------ Struts2是apache项目下的一个web 框架,普遍应用于阿里巴巴、京东等互联网、政府、企业门户网…...

【uni-app】
准备工作(Hbuilder) 1.下载hbuilder,插件使用Vue3的uni-app项目 2.需要安装编译器 3.下载微信开发者工具 4.点击运行->微信开发者工具 5.打开微信开发者工具的服务端口 效果图 准备工作(VScode) 插件 uni-cr…...
Pytorch 多卡并行(3)—— 使用 DDP 加速 minGPT 训练
前文 并行原理简介和 DDP 并行实践 和 使用 torchrun 进行容错处理 在简单的随机数据上演示了使用 DDP 并行加速训练的方法,本文考虑一个更加复杂的 GPT 类模型,说明如何进行 DDP 并行实战MinGPT 是 GPT 模型的一个流行的开源 PyTorch 复现项目ÿ…...
IAM、EIAM、CIAM、RAM、IDaaS 都是什么?
后端程序员在做 ToB 产品或者后台系统时,都不可避免的会遇到账号系统、登录系统、权限系统、日志系统等这些核心功能。这些功能一般都是以 SSO 系统、RBAC 权限管理系统等方式命名,但这些系统合起来有一个专有名词:IAM。 IAM IAM 是 Identi…...
STM32 Cubemx 通用定时器 General-Purpose Timers同步
文章目录 前言简介cubemx配置 前言 持续学习stm32中… 简介 通用定时器是一个16位的计数器,支持向上up、向下down与中心对称up-down三种模式。可以用于测量信号脉宽(输入捕捉),输出一定的波形(比较输出与PWM输出&am…...

Ubuntu 20.04降级clang-format
1. 卸载clang-format sudo apt purge clang-format 2. 安装clang-format-6.0 sudo apt install clang-format-6.0 3. 软链接clang-format sudo ln -s /usr/bin/clang-format-6.0 /usr/bin/clang-format...

激活函数总结(三十四):激活函数补充(FReLU、CReLU)
激活函数总结(三十四):激活函数补充 1 引言2 激活函数2.1 FReLU激活函数2.2 CReLU激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Sof…...

【LeetCode-简单题KMP】459. 重复的子字符串
文章目录 题目方法一:移动匹配方法二:KMP算法 题目 方法一:移动匹配 class Solution {//移动匹配public boolean repeatedSubstringPattern(String s) {StringBuffer str new StringBuffer(s);//ababstr.append(s);//拼接一份自己 abababab…...

Lua脚本
基本语法 注释 print(“script lua win”) – 单行注释 – [[ 多行注释 ]] – 标识符 类似于:java当中 变量、属性名、方法名。 以字母(a-z,A-Z)、下划线 开头,后面加上0个或多个 字母、下划线、数字。 不要用下划线大写字母…...

vue 封装一个Dialog组件
基于element-plus封装一个Dialog组件 <template><section class"dialog-wrap"><el-dialog :title"title" v-model"visible" :close-on-click-modal"false"><section class"content-wrap"><Form…...
外包干了2个月,技术退步明显。。。。。
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
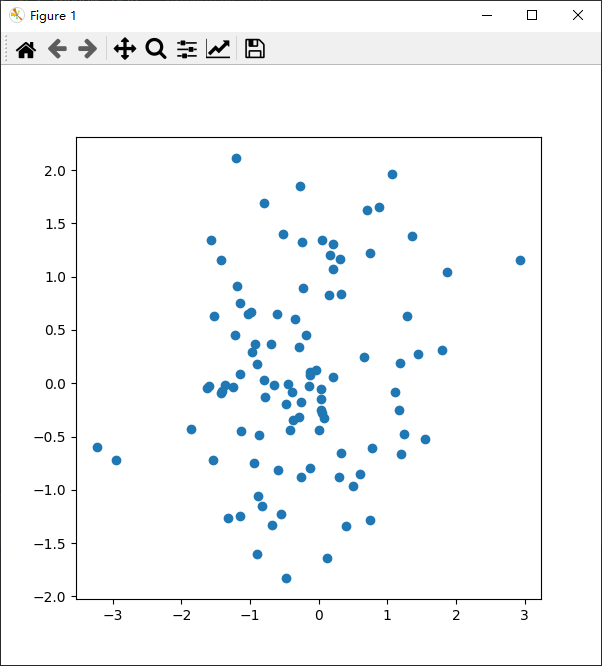
python科研作图
1、气泡图 气泡图是一种在xy轴上显示三个维度的数据的有效方式。在气泡图中,基本上,每个气泡代表一个数据点。横坐标和纵坐标的位置代表两个维度,气泡的大小则代表第三个维度。 在这个例子中,我们用numpy库生成了一些随机数据&a…...

视锥体裁剪射线的算法
射线Ray(直线情况)需要满足的条件: 在视野中显示的粗细均匀,需要分段绘制,每段的粗细根据到视野的距离计算射线model的顶点尽量少以节省性能损耗要满足条件2的话需要对射线进行裁剪,只绘制射线在视锥体内的部分,因此需要计算射线被视锥体裁剪后新的起点和终点 1. 计算三角…...
)
程序员在线周刊(投稿篇)
嗨,大家好!作为一名程序员,并且是一名互联网文章作者,我非常激动地向大家宣布,我们计划推出一份在线周刊,专门为程序员们提供有趣、实用的文章和资讯。而现在,我们正在征集投稿! 是…...
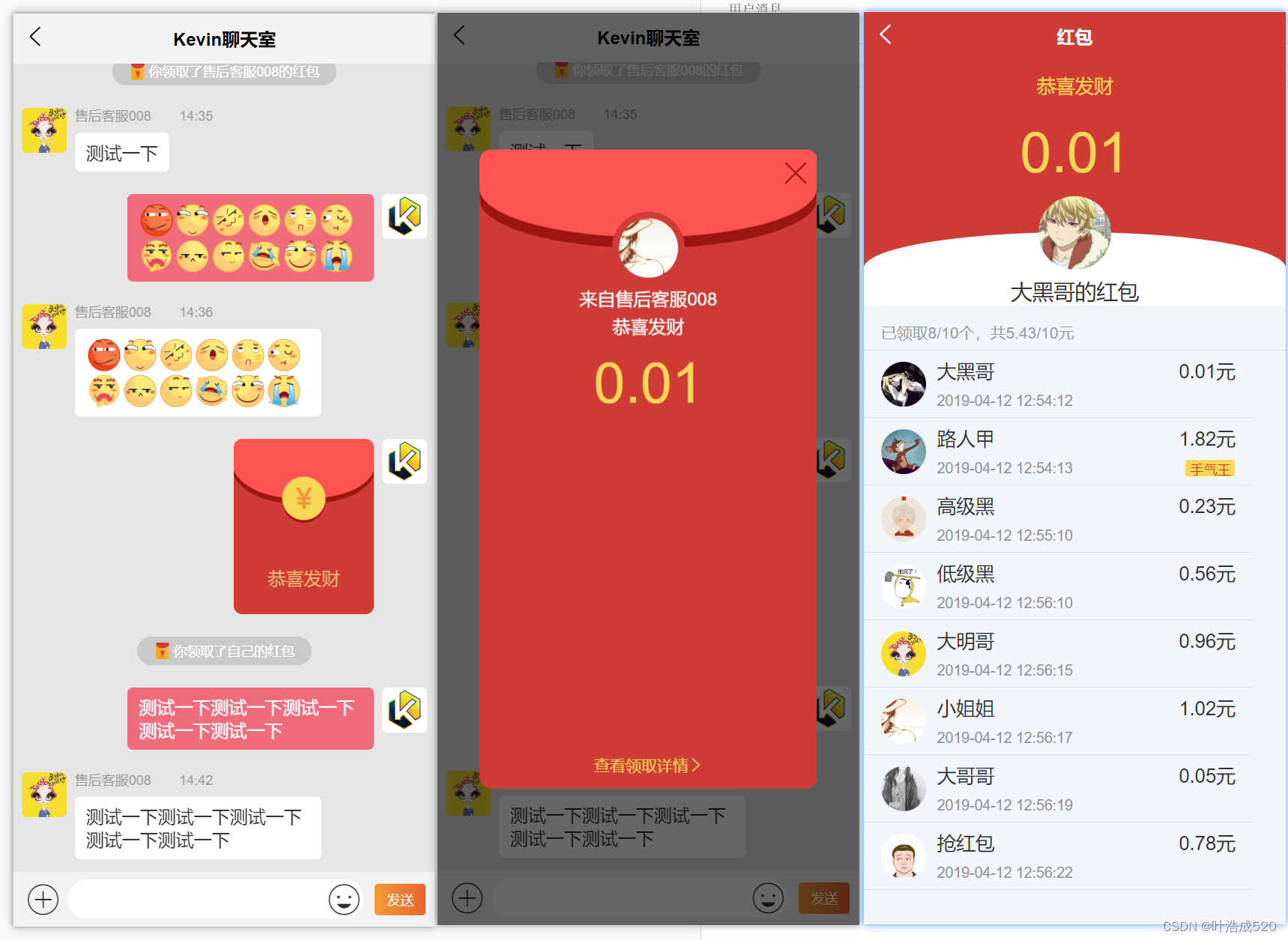
uniapp——实现聊天室功能——技能提升
这里写目录标题 效果图聊天室功能代码——html部分代码——js部分代码——其他部分 首先声明一点:下面的内容是从一个uniapp的程序中摘录的,并非本人所写,先做记录,以免后续遇到相似需求抓耳挠腮。 效果图 聊天室功能 发送图片 …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
