【C语言】【数据存储】用%u打印char类型?用char存128?
1.题目一:
#include <stdio.h>
int main()
{char a = -128;printf("%u\n",a);return 0;
}
%u 是打印无符号整型
解题逻辑:
1. 原反补互换,截断
-128
原码:10000000…10000000
补码:11111111…10000000
(char类型占 1 个字节,8 个bit位)截断:10000000
2.整型提升:
char 默认 signed char 所以高位补符号位:11111111…10000000
3.%u打印的结果:
%u 是打印无符号整型,那么补码 11111111…10000000 中第一个 1 不是符号位,此时原码与补码相同,打印出来的就是二进制11111111…10000000所代表的十进制数:4294967168
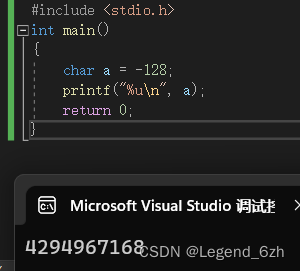
2.题目二:
#include <stdio.h>
int main()
{char a = 128;printf("%u\n",a);return 0;
}
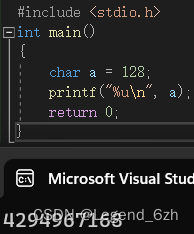
char 类型的存储范围是 -128~127 那么存了 128怎么打印?
必须将 128从低位截断
截断后是 10000000
整型提升:11111111…10000000
(整型提升时,只与变量类型有关,有符号的往高位加符号位,无符号的高位补 0!!)
所以下面的步骤和上一题一样
结果也是4294967168
相关文章:

【C语言】【数据存储】用%u打印char类型?用char存128?
1.题目一: #include <stdio.h> int main() {char a -128;printf("%u\n",a);return 0; }%u 是打印无符号整型 解题逻辑: 1. 原反补互换,截断 -128 原码:10000000…10000000 补码:11111111…10000000…...

git-git命令汇总
1.git 存储永久凭据 git config --global credential.helper store 2.git 查询分支或标签的引用 git show-ref 【标签名|分支名】 3.git 搜索关键分支和tag git tag -l *branch* --sortcommitterdate 4.git 删除标签 git tag -d v1.32 删除标签v1.32,参数d…...

自定义实现简易版ArrayList
文章目录 1.了解什么是顺序表2.实现哪些功能3.初始化ArrayList4.实现功能接口遍历顺序表判断顺序表是否已满添加元素指定下标添加元素自定义下标不合法异常判断顺序表是否为空查找指定元素是否存在查找指定元素返回下标获取指定下标的元素顺序表为空异常修改指定下标元素的值删…...
)
React中的Hooks--useReducer()
首先,useReducer是React提供的一个钩子函数,用于管理组件内部的状态。它可以接收一个reducer函数和初始状态,并返回一个包含状态和更新状态的函数的数组。 与之相反,Redux是一个独立的状态管理库,它可以在整个应用程序…...

DM@数理逻辑@命题公式及其赋值@真值表@公式分类
文章目录 abstract命题公式及其赋值命题常项命题变项 命题公式合式公式(命题公式)限定基本联结词的合适公式的定义合式公式中的0和1子公式 **公式的层次定义**分层加括号 命题公式的赋值和解释成真赋值成假赋值公式的书写规范括号的省略 真值表赋值方法数量构造真值表 公式分类…...

HTTP协议(超级详细)
HTTP协议介绍 基本介绍: HTTP:超文本传输协议,是从万维网服务器传输超文本到本地浏览器的传送协议HTTP是一种应用层协议,是基于TCP/IP通信协议来传送数据的,其中 HTTP1.0、HTTP1.1、HTTP2.0 均为 TCP 实现࿰…...

leetcode做题笔记135. 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。 你需要按照以下要求,给这些孩子分发糖果: 每个孩子至少分配到 1 个糖果。相邻两个孩子评分更高的孩子会获得更多的糖果。 请你给每个孩子分发糖果,计算并返回需要准备的…...
Oracle数据库体系结构(三)_逻辑结构
Oracle逻辑存储结构,主要描述oracle 数据库内部数据的组织和管理方式,即在数据库管理系统的层面中如何组织和管理数据,与操作系统没有关系。逻辑存储结构时候物理存储机构的抽象体现,是不可见的,可以通过查询数据库数据字典了解逻…...

在 Python 中计算两个 GPS 点之间的距离
计算两个 GPS 点之间的距离是我们可以在 Python 框架内操作的地理和数学练习。 现在让我们看看如何使用 Python 执行此操作。 在 Python 中使用 Haversine 公式计算两个 GPS 点之间的距离 haversine 公式是用 Python 计算两个 GPS 点之间距离的一种简化方法,但它的计算是基于…...
影刀RPA解决WPS不存在的问题
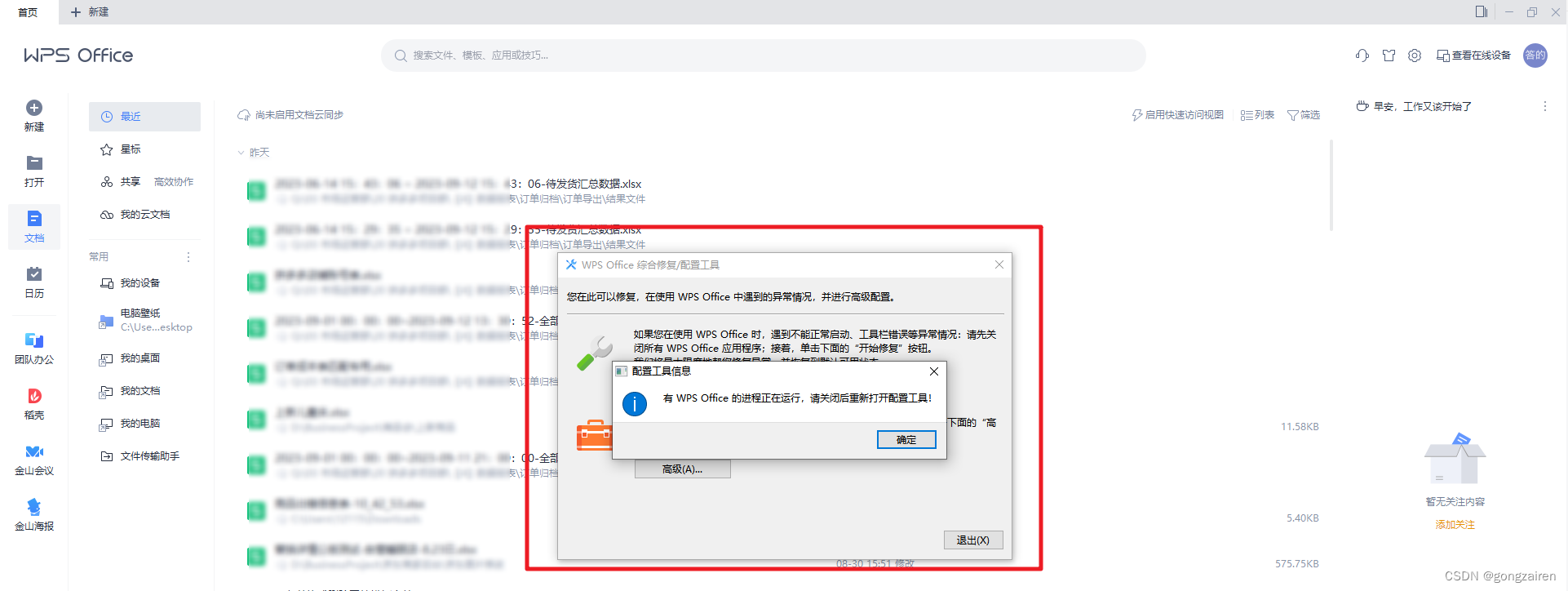
问题阐述 明明电脑上已经安装了WPS,但影刀程序还是提示没有安装的问题 解决办法 1.打开WPS并关闭所有其他网页 2. 配置与修复 3.开始修复 出现这个框,就要关闭WPS,否则无法执行,关闭WPS不影响其修复 4.等待修复完成即可...

vue动态路由切换刷新保留历史路由搜索条件数据
最近有客户反映我们系统按条件查询完列表进入详情页后再返回列表页时页面没有展示他查询的那条数据,而是进入页面一贯会展示按无条件查询的数据,希望我们能对列表做查询缓存,那咱们就用keep-alive来实现一下 AppMain.vue include 属性绑定一个…...

免费:CAD批量转PDF工具,附下载地址
分享一款CAD 批量转PDF、打印的工具插件。能自动识别图框大小、自动识别比例、自动编号命名。重点!重点!重点!自动将CAD的多张图纸一次性地、批量地转为PDF,或者打印。效果看下图: 适用环境: 32位系统 Auto…...

无涯教程-JavaScript - FACT函数
描述 The FACT function returns the factorial of a number. The factorial of a number is equal to 1*2*3*...* number. 语法 FACT (number)争论 Argument描述Required/OptionalNumberThe nonnegative number for which you want the f…...

UART 协议
文章目录 电气层硬件拓扑基本原理协议空闲位起始位数据位奇偶校验位无校验奇校验偶校验mark parityparity 停止位 波特率优缺点优点缺点 参考 UART(universal asynchronous receiver-transmitter) 通用异步收发器 分类特点导线2速度9600, 19200, 38400&…...
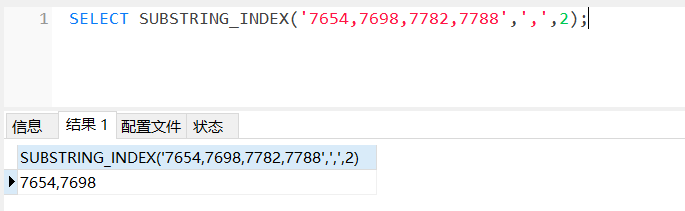
MySql中分割字符串
MySql中分割字符串 在MySql中分割字符串可以用到SUBSTRING_INDEX(str, delim, count) 参数解说 解释 str 需要拆分的字符串 delim 分隔符,通过某字符进行拆分 count 当 count 为正数&…...

Ubuntu 22.04安装过程
iso下载地址 Ubuntu Releases 1.进入引导菜单 选择Try or Install Ubuntu Server安装 2.选择安装语言 默认选择English 3.选择键盘布局 默认即可 4.选择安装服务器版本 最小化安装 5.配置网络 选择ipv4 选择自定义 DHCP也可 6.配置代理 有需要可以配置 这里跳过 7.软件源 …...

【算法|虚拟头节点|链表】移除链表元素
Leetcode203 移除链表元素 题目描述: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出…...
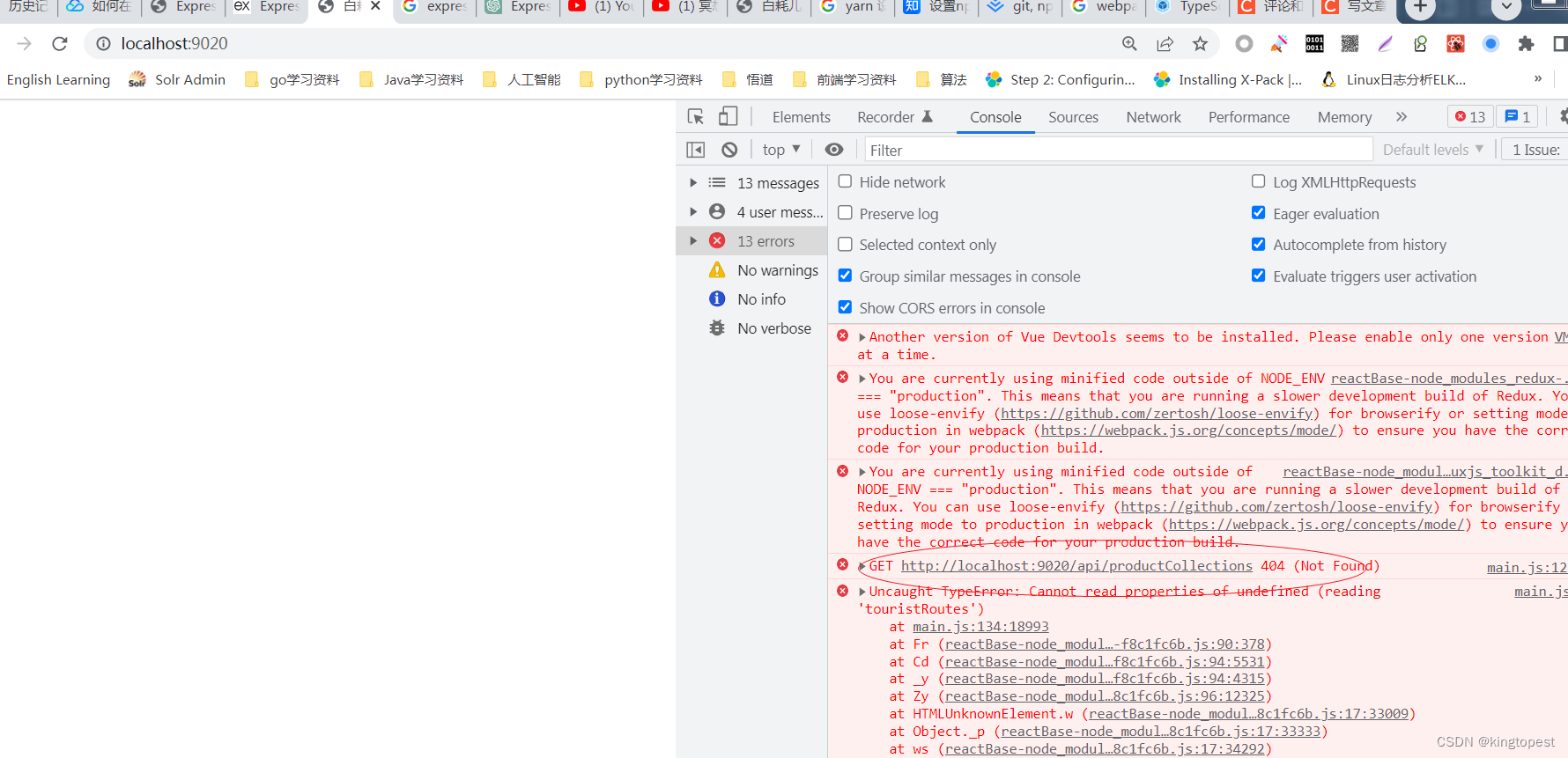
express静态路由匹配引发的404错误
最近有一个react项目,我用webpack打包,然后使用express作为webserver跑起来。 但是在运行的时候,就白屏了,看console原来是报了404错误 可是代码里面明明有路由定义,为什么还是报404错误呢? app.get("…...
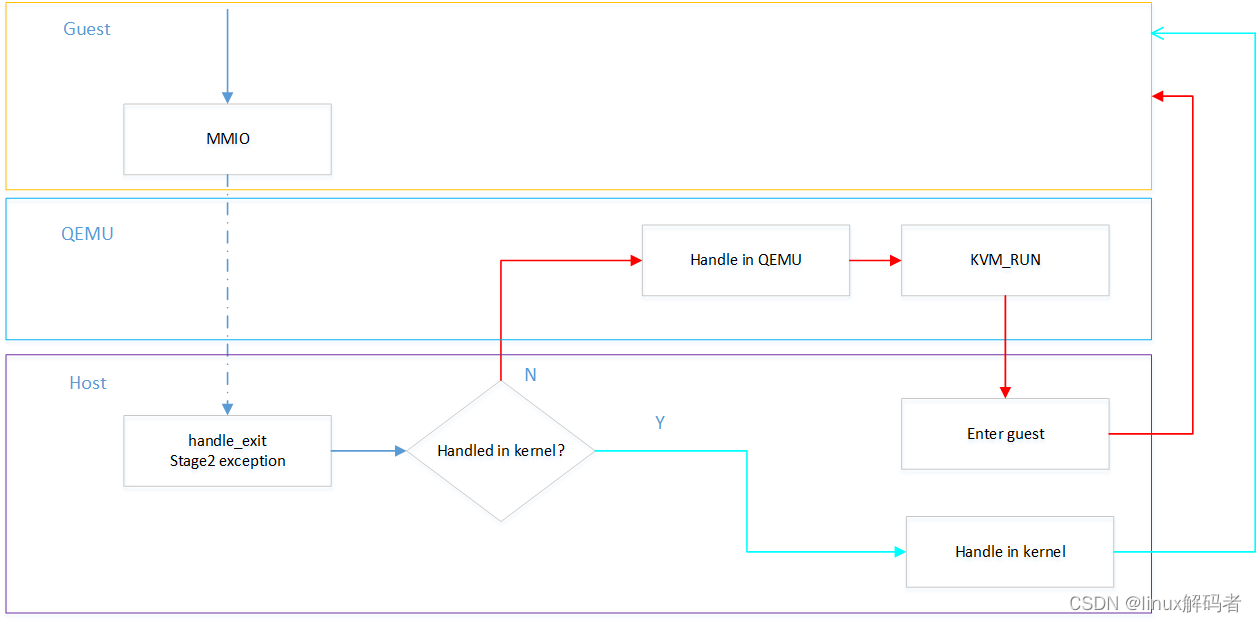
VHOST-SCSI代码分析(4)VHOST KICK机制
在VIRTIO框架中虚拟机通知QEMU数据准备好是通过操作MMIO,在KVM中将操作分发到QEMU中,由QEMU中模拟对应的MMIO操作(图中红色部分)。 VHOST框架虚拟机通知HOST内核数据准备好也是通过MMIO操作,但在函数vhost_dev_enable_…...
)
Docker Volume(存储卷)
文章目录 Docker Volume(存储卷)1.什么是存储卷?2.为什么需要存储卷?3. 存储卷的分类1) 管理卷Volume方式一:Volume命令操作方式二: -v 或者--mount 指定方式三: Dockerfile 匿名卷小结Docker 卷生命周期Docker 卷共享…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
