IMU姿态解算,从IMU数据中计算旋转、速度、位置,IMU测量的原理
0. 预备
a. IMU测量值解释
IMU在测量时,得到的角速度或者加速度均是相对于地心惯性系结果,并且将该结果表示到Body坐标系下,就形成了最终的IMU输出。
记作: ω i b b \omega_{ib}^b ωibb,表示body系相对于惯性系的角速度测量在body下的表示。
a b i b a_{bi}^b abib,表示body系相对于惯性系的加速度测量在body系下的表示。
b. IMU加速度计误差建模
a ~ i b b = a i b b + g b + b a + n a \tilde a_{ib}^b = a_{ib}^b + g^b + b^a + n^a a~ibb=aibb+gb+ba+na
其中: a ~ i b b \tilde a_{ib}^b a~ibb 表示的是IMU最终输出的测量值;
a i b b a_{ib}^b aibb 表示的是当前的加速度真值,去除了各种误差;
g b g^b gb重力加速度在body系下的表示;
b a b^a ba 加速度计的bias,它是一个恒定偏差,并且随时间缓慢变化;
n a n^a na加速度计的随机测量噪声,建模为0均值高斯噪声。
对于上式的加速度计建模,有时候也会建模到导航系下,多数情况下重力加速度是在导航系下有比较简洁的表示 [ 0 , 0 , g ] T [0, 0, g]^T [0,0,g]T,因此如果将加速度计的测量转到导航下就可以直接在导航系中简单的处理重力加速度。因此在实际使用时,有时也可以建模为如下形式:
a ~ i b b = R b w ( a i b w + g w ) + b a + n a \tilde a_{ib}^b = R_{bw} (a_{ib}^w + g^w) + b^a + n^a a~ibb=Rbw(aibw+gw)+ba+na
c. IMU陀螺仪误差建模
ω ~ i b b = ω i b b + b g + n g \tilde \omega_{ib}^b = \omega_{ib}^b + b^g + n^g ω~ibb=ωibb+bg+ng
其中: ω ~ i b b \tilde \omega_{ib}^b ω~ibb表示的是IMU最终输出的角速度测量值;
ω i b b \omega_{ib}^b ωibb表示的是当前的角速度真值,去除了各种误差;
b g b^g bg 陀螺仪的bias,并且随时间缓慢变化,短时间内可以认为是一个恒定偏差;
n g n^g ng 陀螺仪的随机测量噪声,建模为0均值高斯噪声。
d. 考虑地球自转时的各个角速度关系
ω i n n = ω i e n + ω e n n \omega_{in}^n = \omega_{ie}^n + \omega_{en}^n ωinn=ωien+ωenn
其中: ω i n n \omega_{in}^n ωinn 表示导航系相对于惯性系的角速度在导航下的表示
ω i e n \omega_{ie}^n ωien表示地球相对于惯性系的自转角速度在导航下的表示
ω e n n \omega_{en}^n ωenn 表示导航系相对于地球的角速度在导航下的表示
IMU测量的角速度是相对于惯性系i,而多数情况下进行导航姿态计算时是在导航系下的,也就是说如果直接使用IMU的角速度进行解算,就会把地球自转以及导航系变化带来的角速度都会引入到系统中,在高精度的IMU中这会带来误差,对于MEMS的IMU而言,可以忽略这一点。
对于 ω i e n \omega_{ie}^n ωien的计算如下:
ω i e n = [ 0 ω i e cos L ω i e sin L ] \omega_{ie}^n = [0 \quad \omega_{ie} \cos L \ \quad \omega_{ie} \sin L] ωien=[0ωiecosL ωiesinL]
其中: ω i e \omega_{ie} ωie是地球的自转角速度,取 7.2921151467 × 1 0 − 5 r a d / s 7.2921151467 \times 10^{-5} rad/s 7.2921151467×10−5rad/s。参考《捷联惯导算法与组合导航原理》 P54
L L L是当前位置对应的地理纬度
对于 ω e n n \omega_{en}^n ωenn的计算如下:
ω e n n = [ − v N R M + h v E R N + h v E R N + h tan L ] \omega_{en}^n = [-\frac{v_N}{R_M + h} \quad \frac{v_E}{R_N + h} \quad \frac{v_E}{R_N+h}\tan L] ωenn=[−RM+hvNRN+hvERN+hvEtanL]
其中: v E v_E vE, v N v_N vN是当前时刻载体在东北天坐标系下的速度分量
R M , R N R_M,R_N RM,RN分别为子午圈主曲率半径和卯酉圈曲率半径 R N R_N RN,计算方法如下:参考《捷联惯导算法与组合导航原理》 P46和P48
R N = R e 1 − e 2 sin 2 L R_N = \frac{R_e}{\sqrt{1 - e^2 \sin^2 L}} RN=1−e2sin2LRe
R M = R e ( 1 − e 2 ) ( 1 − e 2 sin 2 L ) 3 2 R_M = \frac{R_e(1-e^2)}{(1-e^2 \sin^2 L)^{\frac{3}{2}}} RM=(1−e2sin2L)23Re(1−e2)
L , h L,h L,h分别是当前位置对应的地理纬度和高度
注意:上面介绍了IMU的误差建模,但是后续的推导均未考虑误差
1. 姿态更新
参考《捷联惯导算法与组合导航原理》 P79
a.惯性系下的IMU姿态解算
C ˙ b i = C b i ∗ ( ω i b b × ) \dot C_b^i = C_b^i * (\omega_{ib}^b \times) C˙bi=Cbi∗(ωibb×)
上式是IMU的姿态的微分方程。如果要在惯性系下对上式进行解微分方程,即可得到IMU姿态计算结果。结果如下:
C b ( m ) i = C b ( m − 1 ) i C b ( m ) b ( m − 1 ) C_{b(m)}^{i} = C_{b(m-1)}^i C_{b(m)}^{b(m-1)} Cb(m)i=Cb(m−1)iCb(m)b(m−1)
其中: C b ( m ) i C_{b(m)}^{i} Cb(m)i 表示m时刻,b系到i的变换矩阵
C b ( m ) b ( m − 1 ) C_{b(m)}^{b(m-1)} Cb(m)b(m−1) 表示由b系在m时刻到m-1时刻的变化矩阵,它就是有IMU的角速度测量计算而来。
需要格外的关注的是 C b ( m ) b ( m − 1 ) C_{b(m)}^{b(m-1)} Cb(m)b(m−1)的计算,它是IMU姿态计算的关键,如果m-1时刻到m是IMU符合定轴转动,则由下式严格成立:
C b ( m ) b ( m − 1 ) = e ∫ t m − 1 t m ω i b b ( t ) d t C_{b(m)}^{b(m-1)} = e^{\int_{t_{m-1}}^{t_m} \omega_{ib}^b(t) dt} Cb(m)b(m−1)=e∫tm−1tmωibb(t)dt
注意:上式是在定轴假设下才严格成立的,所谓定轴转动就是角速度的方向不发生变化,但是很显然这个假设在实际情况下不严格成立,但是幸运的是目前的IMU都是高频率的IMU它一次测量内很接近定轴转动。对于 e ∫ t m − 1 t m ω i b b ( t ) d t e^{\int_{t_{m-1}}{t_m} \omega_{ib}^b(t) dt} e∫tm−1tmωibb(t)dt的计算有多种方式,有欧拉积分,中值积分,矢量二子样算法,单子样+前一周期等算法。参考《捷联惯导算法与组合导航原理》 P28~P30。尽管解算方法很多,但是对于消费级的MEMS IMU使用中值积分就足够使用。
b.导航系下的IMU姿态解算
上面的过程是围绕着参考系为i系进行的,多数情况下我们在使用时都是用的导航系,下面就以东北线(ENU)导航系对IMU姿态解算进行推导介绍。导航下旋转矩阵对时间的微分方程如下:
C ˙ b n = C b n ∗ ( ω n b b × ) \dot C_b^n = C_b^n * (\omega_{nb}^b \times) C˙bn=Cbn∗(ωnbb×)
当考虑上地球转速以及导航系变化的角速度时, ω n b b = ω i b b − ω i n b \omega_{nb}^b = \omega_{ib}^b - \omega_{in}^b ωnbb=ωibb−ωinb,上式可以进一步列写为:
C ˙ b n = C b n ∗ ( ω n b b × ) = C b n [ ( ω i b b − ω i n b ) × ] = C b n ( ω i b b × ) − ( ω i n n × ) C b n \dot C_b^n = C_b^n * (\omega_{nb}^b \times) = C_b^n[(\omega_{ib}^b - \omega_{in}^b)\times] = C_b^n(\omega_{ib}^b \times) - (\omega_{in}^n\times)C_b^n C˙bn=Cbn∗(ωnbb×)=Cbn[(ωibb−ωinb)×]=Cbn(ωibb×)−(ωinn×)Cbn
对上式进行求微分方程,并进行离散化就可以得到导航系下的姿态更新方法。但是求解比较麻烦,可以采用矩阵链式法则进行求解:
C b ( m ) n ( m ) = C n ( m − 1 ) n ( m ) C i n ( m − 1 ) C b ( m − 1 ) i C b ( m ) b ( m − 1 ) = C n ( m − 1 ) n ( m ) C b ( m − 1 ) n ( m − 1 ) C b ( m ) b ( m − 1 ) C_{b(m)}^{n(m)} = C_{n(m-1)}^{n(m)}C_{i}^{n(m-1)}C_{b(m-1)}^i C_{b(m)}^{b(m-1)} = C_{n(m-1)}^{n(m)} C_{b(m-1)}^{n(m-1)} C_{b(m)}^{b(m-1)} Cb(m)n(m)=Cn(m−1)n(m)Cin(m−1)Cb(m−1)iCb(m)b(m−1)=Cn(m−1)n(m)Cb(m−1)n(m−1)Cb(m)b(m−1)
其中: C n ( m − 1 ) n ( m ) C_{n(m-1)}^{n(m)} Cn(m−1)n(m) 表示m-1时刻到m时刻导航系发生的姿态变化,也相当于在m时刻对应的导航系下表示m-1时刻导航系的位姿,计算方法是使用 ω i n n = ω i e n + ω e n n \omega_{in}^n = \omega_{ie}^n + \omega_{en}^n ωinn=ωien+ωenn.
C b ( m − 1 ) n ( m − 1 ) C_{b(m-1)}^{n(m-1)} Cb(m−1)n(m−1) 表示m-1时刻IMU相对于导航系的姿态
C b ( m ) b ( m − 1 ) C_{b(m)}^{b(m-1)} Cb(m)b(m−1) 表示m时刻到m-1时刻IMU发生的位姿变化,它来自于IMU角速度测量的积分。
c. 导航系简化版姿态计算
C b ( m ) n ( m ) = C n ( m − 1 ) n ( m ) C b ( m − 1 ) n ( m − 1 ) C b ( m ) b ( m − 1 ) C_{b(m)}^{n(m)} = C_{n(m-1)}^{n(m)} C_{b(m-1)}^{n(m-1)} C_{b(m)}^{b(m-1)} Cb(m)n(m)=Cn(m−1)n(m)Cb(m−1)n(m−1)Cb(m)b(m−1)
在MEMS IMU中上式可以忽略导航系的运动 C n ( m − 1 ) n ( m ) C_{n(m-1)}^{n(m)} Cn(m−1)n(m),因为消费级普通IMU无法敏感到这一项,所以可以忽略。于是可以得到简化版的姿态解算:
C b ( m ) n ( m ) = C b ( m − 1 ) n ( m − 1 ) C b ( m ) b ( m − 1 ) C_{b(m)}^{n(m)} = C_{b(m-1)}^{n(m-1)} C_{b(m)}^{b(m-1)} Cb(m)n(m)=Cb(m−1)n(m−1)Cb(m)b(m−1)
其中, C b ( m ) b ( m − 1 ) = e ∫ t m − 1 t m ω i b b ( t ) d t C_{b(m)}^{b(m-1)} = e^{\int_{t_{m-1}}^{t_m} \omega_{ib}^b(t) dt} Cb(m)b(m−1)=e∫tm−1tmωibb(t)dt,对于它的求解与前述思路一样,可以采用欧拉积分,中值积分等求解 ∫ t m − 1 t m ω i b b ( t ) d t {\int_{t_{m-1}}^{t_m} \omega_{ib}^b(t) dt} ∫tm−1tmωibb(t)dt,然后使用罗德里格斯公式完成指数映射。
2. 速度更新
参考《捷联惯导算法与组合导航原理》 P81
a. 精确速度微分建模
v ˙ e n n = C b n f s f b − 2 ( w i e n + w e n n ) × v e n n + g n \dot v_{en}^n = C_b^n f_{sf}^b - 2(w_{ie}^n+w_{en}^n) \times v_{en}^n + g^n v˙enn=Cbnfsfb−2(wien+wenn)×venn+gn
其中: f s f b f_{sf}^b fsfb 为加速度计测量的比力
− 2 ( w i e n + w e n n ) × v e n n - 2(w_{ie}^n+w_{en}^n) \times v_{en}^n −2(wien+wenn)×venn 为有害加速度
g n g^n gn 为重力加速度
以上便是对导航系下载体速度的精确微分建模,对其积分即可得到速度的解算,具体过程比较复杂,参考《捷联惯导算法与组合导航原理》 P82。
在IMU加速度误差的建模中使用的是加速度一词,这里使用的是比力,实际上可以认为它们是同样的意义。
b. 简化版速度微分建模
在MEMS IMU中,有害加速度这一项可以忽略,并忽略一些类似划桨误差等,可以得到简化版的速度更新方程:
v ˙ e n n = C b n f s f b + g n \dot v_{en}^n = C_b^n f_{sf}^b + g^n v˙enn=Cbnfsfb+gn
上式求积分之后改写成递推的形式为:
v m n ( m ) = v m − 1 n ( m − 1 ) + Δ v s f ( m ) n v_{m}^{n(m)} = v_{m-1}^{n(m-1)} + \Delta v_{sf(m)}^n vmn(m)=vm−1n(m−1)+Δvsf(m)n
其中: v m − 1 n ( m − 1 ) v_{m-1}^{n(m-1)} vm−1n(m−1)为m-1时刻载体速度在导航下的表示。
Δ v s f ( m ) n = ∫ m − 1 m ( C b n f s f b + g n ) d t \Delta v_{sf(m)}^n = \int_{m-1}^m (C_b^n f_{sf}^b + g^n)dt Δvsf(m)n=∫m−1m(Cbnfsfb+gn)dt
上式的求解可以采用欧拉积分,中值积分等完成。
3. 位置更新
对于位置的更新,在参考《捷联惯导算法与组合导航原理》 P87 中采用的是经纬高来表示位置。而实际使用中多以导航系原点来表示位置,因此此处不总结介绍经纬高的方式。将直接在导航系下进行解算。
p ˙ n ( m ) = v n ( m ) \dot p^{n(m)} = v^{n(m)} p˙n(m)=vn(m)
对上式进行欧拉积分,即可得到递推方程:
p n ( m ) = p n ( m − 1 ) + ∫ m − 1 m v n ( t ) d t p^{n(m)} = p^{n(m-1)} + \int_{m-1}^m v^{n}(t)dt pn(m)=pn(m−1)+∫m−1mvn(t)dt
同样的方式,可以采用欧拉积分,中值积分等对 ∫ m − 1 m v n ( t ) d t \int_{m-1}^m v^{n}(t)dt ∫m−1mvn(t)dt进行求解。
例如,使用中值积分,并假设m-1到m时刻速度为线性变化,则有如下式:
p n ( m ) = p n ( m − 1 ) + v n ( m − 1 ) ∗ Δ t + 1 2 ( f s f n ( m − 1 ) + g n ) Δ t 2 p^{n(m)} = p^{n(m-1)} + v^{n(m-1)}*\Delta t + \frac{1}{2} (f_{sf}^{n(m-1)} +g^n) \Delta t^2 pn(m)=pn(m−1)+vn(m−1)∗Δt+21(fsfn(m−1)+gn)Δt2
注意:IMU的姿态解算过程比较复杂,在建模时可以做的非常精确,这会导致模型非常复杂,实际当中使用时,普通的MEMS IMU无需做复杂的建模,不需要考虑地球转速,导航系的运动,速度划桨误差等等。当我们有了IMU初始时刻的姿态、速度、位置之后,就可以使用上述的递推方式计算出后续的姿态变化。但是对于低精度的IMU这个递推的过程维持不了多久就会发散。
相关文章:

IMU姿态解算,从IMU数据中计算旋转、速度、位置,IMU测量的原理
0. 预备 a. IMU测量值解释 IMU在测量时,得到的角速度或者加速度均是相对于地心惯性系结果,并且将该结果表示到Body坐标系下,就形成了最终的IMU输出。 记作: ω i b b \omega_{ib}^b ωibb,表示body系相对于惯性系的…...
【Qt-17】Qt调用matlab生成的dll库
matlab生成dll库 1、matlab示例代码 function BDCube(x,y)[x,y,z] cylinder(x,y);t1 hgtransform;s1 surf(3*x,3*y,4*z,Parent,t1);grid onview(3)shading interp end 2、matlab环境配置 首先检查自己的mcc编译器是否可用,输出以下命令: &#x…...
)
css经典面试题(二)
文章目录 1、清除浮动2、opacity: 0、visibility: hidden、display: none 的区别3、css画一个三角形4、常见的主流浏览器前缀5、重绘与重排的区别?6、如何优化图片7、CSS3 中 transition 和 animation 的属性分别有哪些8、居中为什么要使用 transform(为…...

jira搜索search issue条目rest实用脚本
官方文档链接地址: The Jira Cloud platform REST API 实用json请求脚本如下: {"fields": ["summary","status"],"jql": "project abc AND summary ~ 【%s】【coverity】 AND componentCoverity"…...

《C++ primer plus》精炼(OOP部分)——对象和类(5)
“学习是照亮心灵的火炬,它永不熄灭,永不止息。” 文章目录 类的自动和强制类型转换原始类型转换为自定义类型将自定义类型转换为原始类型 类的自动和强制类型转换 原始类型转换为自定义类型 可以用一个参数的构造函数来实现,例如ÿ…...

钉钉旧版服务端SDK支持异步方法的升级改造
最近项目中需要对接钉钉,有些钉钉 API 的访问需要使用旧版服务端 SDK 才能搞定,但是这个 SDK 使用的还是 .NET Framework 2.0 框架,不能跨平台部署,也不支持 async\await 的异步操作方法,Nuget 上也有其它用户改造的 .…...
【C语言】【数据存储】用%d打印char类型数据,猜结果是啥
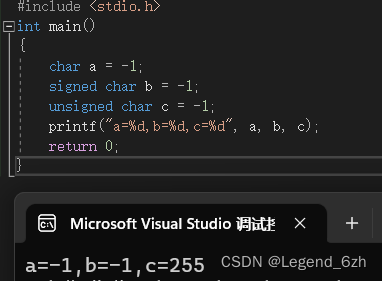
题目代码如下: #include <stdio.h> int main() {char a -1;signed char b-1;unsigned char c-1;printf("a%d,b%d,c%d",a,b,c);return 0; }解题关键: 1.二进制存储:原码,反码,补码 互换 2.截断 3.整型…...

算法——双指针
1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode) 这道题的重点是,如何用最小的操作数,来使其x变为0——也可以看作是用最少的数据个数,来求和得到x。 ——但是我们可以知道,由于数据是从两端向中间取的…...
【PowerQuery】Excel的PowerQuery按需刷新
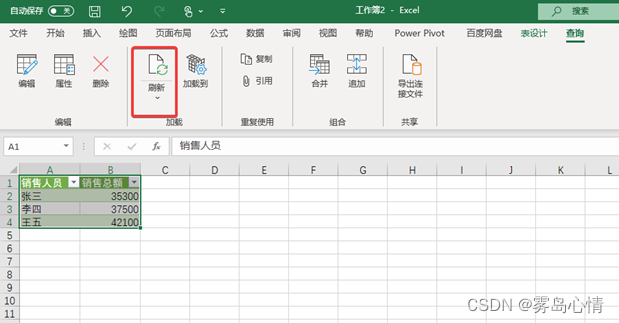
将数据通过PowerQuery 导入进来后,这里将进行数据分组运算,最终的数据计算结果将保存在Excel 表格中,图为销售统计结果。 在Excel中,如果我们希望进行销售统计的手动更新可以使用几种不同的方法来进行刷新: 刷新单一数据连接如果仅仅需要刷新单一数据连接的话我们可以通过…...

Django REST Farmowork初探
1.简介 Django REST framework (简称:DRF)是一个强大而灵活的 Web API 工具。 遵循RESTFullAPI风格,功能完善,可快速开发API平台。 官网文档:https://www.django-rest-framework.org 2. framwork的安装 …...

【flink进阶】-- Flink kubernetes operator 版本升级
目录 1、检查当前 flink kubernetes operator 版本 2、停止生产上正在运行的 flink job 3、升级 CRD...
Linux Ubuntu20.04深度学习环境快速配置命令记录
一、驱动安装 1、更新系统包 sudo apt-get updatesudo apt-get upgrade 2、安装显卡驱动 使用apt方式安装驱动,多数情况不容易成功, 使用一下方法更佳: 1.查看合适显卡的驱动版本 ubuntu-drivers devices NVIDIA GeForce 驱动程序 - …...

信息安全三级真题一
目录 一、单选题 二、填空题 三、综合题 一、单选题 二、填空题 三、综合题 知法懂法,请各位网络安全从业者遵守《网络安全法》、《个人信息保护法》 业%$务*$&联&#系 XHU3ZjUxXHU3ZWRjXHU4ZmQwXHU3ZWY0XHU2ZTE3XHU5MDBmXHU1NmUyXHU5NjFmXHUyMDBiXHU2M…...

RK3568-tftp更新设备树和内核nfs挂载文件系统
1. 注意:需要设备树和内核按以下修改才能支持tftp和nfs。 1.1 修改设备树: diff --git a/arch/arm64/boot/dts/rockchip/OK3568-C-linux.dts b/arch/arm64/boot/dts/rockchip/OK3568-C-linux.dts index 178b4d831..34cb57ffd 100644 --- a/arch/arm64/boot/dts/rockchip/OK…...
FIR滤波器简述及FPGA仿真验证
数字滤波器的设计,本项目做的数字滤波器准确来说是FIR滤波器。 FIR滤波器(有限冲激响应滤波器),与另一种基本类型的数字滤波器——IIR滤波器(无限冲击响应滤波器)相对应,其实就是将所输入的信号…...
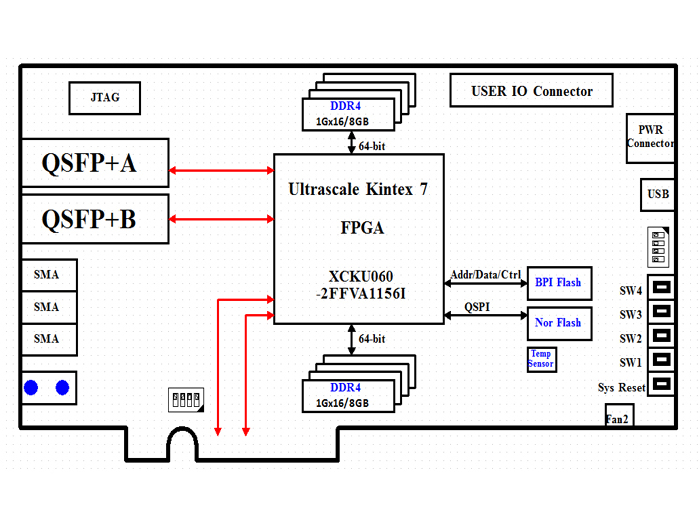
高速信号处理板资料保存:383-基于kintex UltraScale XCKU060的双路QSFP+光纤PCIe 卡设计原理图
基于kintex UltraScale XCKU060的双路QSFP光纤PCIe 卡 一、板卡概述 本板卡系我司自主研发,基于Xilinx UltraScale Kintex系列FPGA XCKU060-FFVA1156-2-I架构,支持PCIE Gen3 x8模式的高速信号处理板卡,搭配两路40G QSFP接口…...
QT:使用分组框、单选按钮、普通按钮、标签、行编辑器、垂直分布、水平分布做一个小项目
widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QRadioButton> //单选按钮 #include <QGroupBox> //分组框 #include <QHBoxLayout> //水平布局 #include <QVBoxLayout> //垂直布局 #include <QPushButton>…...

封装微信小程序隐私信息授权
隐私 代码 html (modal 组件再后面封装有提供) <modal isShow"{{show}}"><view class"privacy-auth-dialog"><view class"title">温馨提示</view><view class"content"><vi…...
【C#】FileInfo类 对文件进行操作
提示:使用FileInfo类时,要引用System.IO命名空间。 using System.IO; FileInfo类 生成文件删除文件移动文件复制文件获取文件名判断文件是否存在属性列表其它常用方法 生成文件 Create():在指定路径上创建文件。 FileInfo myFile new FileIn…...

python中的字符串也是可迭代对象吗?
python中的字符串也是可迭代对象吗? ━━━━━━━━━━━━━━━━━━━━━━ 是的,Python中的字符串是可迭代对象。这意味着你可以像处理列表或元组那样处理字符串。例如,你可以使用for循环遍历字符串中的每个字符,或…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
