卡尔曼滤波(Kalman Filter)原理浅析-数学理论推导-1
目录
- 前言
- 数学理论推导
- 1. 递归算法
- 2. 数学基础
- 结语
- 参考
前言
最近项目需求涉及到目标跟踪部分,准备从 DeepSORT 多目标跟踪算法入手。DeepSORT 中涉及的内容有点多,以前也就对其进行了简单的了解,但是真正去做发现总是存在这样或者那样的困惑,头疼,果然欠下的总该还的😂
一个个来吧,这个系列文章主要分享博主在学习 DeepSORT 中的 Kalman Filter 的相关知识,主要从两方面分享,一方面是数学理论推导,另一方面是比较通俗易懂的图例分析。
这篇文章主要分享从数学理论推导的方式去理解卡尔曼滤波器,包括递归算法和数学基础
博主为初学者,欢迎交流讨论,若有问题欢迎各位看官批评指正!!!😄
数学理论推导
视频链接:【卡尔曼滤波器】_Kalman_Filter_全网最详细数学推导
注:博主也就把 DR_CAN 老师讲解的内容复述了一遍,强烈建议大家观看原视频!!!
1. 递归算法
我们将系统的学习卡尔曼滤波器,由浅入深
首先我们来初尝下递归算法的味道,谈到卡尔曼滤波器(Kalman Filter),这个 Filter 这个词在这里面并不是很能准确地体现出来它的特性。
Kalman Filter 如果用一句话来总结,它是一种 optimal recursive data processing algorithm
它是一种算法,是最优化的、递归的数字处理的算法。它更像是一种观测器,而不是一般意义上的滤波器。卡尔曼滤波器的应用非常广泛尤其是在导航当中,它的广泛应用是因为我们生活的世界中存在着大量的不确定性。当我们去描述一个系统的时候,这个不确定性主要体现在三个方面:
1. 不存在完美的数学模型
2. 系统的扰动往往是不可控的,也是很难建模的
3. 测量的传感器本身存在误差
下面我们来看一个例子,找不同的人用一个尺子去测量一个硬币的直径

这里面我们用 Z k Z_k Zk 来表示测量的结果,下标 k k k 就代表了第 k k k 次的测量结果,因为每个人测量的值都不一样,而且这个尺子本身也有误差,所以说每次测量的结果也会不尽相同。比如说前三次测量的结果分别为 Z 1 = 50.1 m m Z_1 = 50.1mm Z1=50.1mm Z 2 = 50.4 m m Z_2 = 50.4mm Z2=50.4mm Z 3 = 50.2 m m Z_3 = 50.2mm Z3=50.2mm,这个时候如果我让你去估计一下这个真实结果, 很自然的, 你就会想到去取一个平均值就可以了。
如果用数学来表达,这边我们用 X ^ k \hat{X}_k X^k 来表示第 k k k 次的估计值,其计算如下所示:
X ^ k = 1 k ( Z 1 + Z 2 + ⋅ ⋅ ⋅ + Z k ) = 1 k ( Z 1 + Z 2 + ⋅ ⋅ ⋅ + Z k − 1 ) + 1 k Z k = 1 k k − 1 k − 1 ( Z 1 + Z 2 + ⋅ ⋅ ⋅ + Z k − 1 ) + 1 k Z k = k − 1 k X ^ k − 1 + 1 k Z k = X ^ k − 1 − 1 k X ^ k − 1 + 1 k Z k \begin{aligned} \hat{X}_k &= \frac{1}{k} (Z_1 + Z_2 + \cdot\cdot\cdot + Z_k) \\ &= \frac{1}{k} (Z_1 + Z_2 + \cdot\cdot\cdot + Z_{k-1}) + \frac{1}{k}Z_k \\ &= \frac{1}{k} \frac{k-1}{\color{blue}k-1} \color{blue} (Z_1 + Z_2 + \cdot\cdot\cdot + Z_{k-1})\color{black} + \frac{1}{k}Z_k \\ &= \frac{k-1}{k} \color{blue}\hat{X}_{k-1} \color{black} + \frac{1}{k}Z_k \\ &= \hat{X}_{k-1}-\frac{1}{k}\hat{X}_{k-1}+\frac{1}{k}Z_k \end{aligned} X^k=k1(Z1+Z2+⋅⋅⋅+Zk)=k1(Z1+Z2+⋅⋅⋅+Zk−1)+k1Zk=k1k−1k−1(Z1+Z2+⋅⋅⋅+Zk−1)+k1Zk=kk−1X^k−1+k1Zk=X^k−1−k1X^k−1+k1Zk
重新整理下可得到第 k k k 次数的估计值 X ^ k \hat{X}_k X^k 等于下式:
X ^ k = X ^ k − 1 + 1 k ( Z k − X ^ k − 1 ) \hat{X}_k = \hat{X}_{k-1} + \frac{1}{k}(Z_k - \hat{X}_{k-1}) X^k=X^k−1+k1(Zk−X^k−1)
去分析下这个公式,你可以看到随着 k k k 的增加,即随着次数的增加, 1 k → 0 \frac{1}{k} \to 0 k1→0, X ^ k → X ^ k − 1 \hat{X}_k \to \hat{X}_{k-1} X^k→X^k−1,也就是说随着 k k k 的增加,测量的结果就不再重要了。这个也非常好理解,当你有了大量的数据之后,测量了很多次以后,你就对估计的结果很有信心了,所有以后的测量值就变得不那么重要了。而相反当 k k k 值比较小的时候,这个 1 k \frac{1}{k} k1 就会比较大,那这个时候测量的结果就可以起到很大的作用,尤其是它和估计值差距比较大的时候。
下面我们把这个公式提炼出来,我们令 1 k \frac{1}{k} k1 等于 K k \color{blue}K_k Kk,则:
X ^ k = X ^ k − 1 + K k ( Z k − X ^ k − 1 ) \hat{X}_k = \hat{X}_{k-1} + \color{blue}{K}_k \color{black}(Z_k - \hat{X}_{k-1}) X^k=X^k−1+Kk(Zk−X^k−1)
它所代表的意思就是:
当前的估计值 = 上一次的估计值 + 系数 × ( 当前测量值 − 上一次的估计值 ) 当前的估计值 \color{green}= \color{black}上一次的估计值 \color{green} + \color{blue}系数 \color{green} \times \color{black}(当前测量值 \color{green}- \color{black}上一次的估计值) 当前的估计值=上一次的估计值+系数×(当前测量值−上一次的估计值)
在卡尔曼滤波器里面,这个 K k \color{blue}K_k Kk 就代表了卡尔曼增益(Kalman Gain),或者叫做卡尔曼因数。通过这个公式可以看出来,新的估计值 X ^ k \hat{X}_k X^k 与上一次的估计值 X ^ k − 1 \hat{X}_{k-1} X^k−1 有关,然后上一次的又会与上上次的有关,这就是一种递归的思想。而且这也是卡尔曼滤波器的一个优势,它不需要去追溯很久以前的数据,只需要上一次的就可以了。
而关于这个 Kalman Gain K k \color{blue}{K_k} Kk,在这里先做一个最简单的讨论,让大家有一个初步的认识,首先先引入两个参数,一个是估计误差,也就是估计值和真实值的差距,我们用 e E S T e_{EST} eEST 表示,上面的 e e e 代表 Error 误差,下标的 E S T EST EST 就代表 Estimate 估计,还有一个是测量误差,也就是测量值和真实值的差距,用 e M E A e_{MEA} eMEA 来表示,下标的 M E A MEA MEA 就代表 Measurement 测量
Kalman Gain 就等于下式:
K k = e E S T k − 1 e E S T k − 1 + e M E A k \color{blue}{K_k} \color{black} = \frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_{k}}} Kk=eESTk−1+eMEAkeESTk−1
也就是第 k − 1 k-1 k−1 次的估计误差除以第 k − 1 k-1 k−1 的估计误差加上第 k k k 次的测量误差,这个公式实际上就是卡尔曼滤波器的核心公式。我们会在后面的分析中详细的讲解
它是怎么被推导出来的呢?🤔
这个时候我们先来分析一下它,在 k k k 时刻当 e E S T k − 1 ≫ e M E A k {e_{EST_{k-1}} \gg e_{MEA_{k}}} eESTk−1≫eMEAk 时 K k → 1 \color{blue}{K_k} \to 1 Kk→1 , X ^ k = X ^ k − 1 + Z k − X ^ k − 1 = Z k \hat{X}_k = \hat{X}_{k-1} + Z_k - \hat{X}_{k-1} = Z_k X^k=X^k−1+Zk−X^k−1=Zk,这就说明了当 k − 1 k-1 k−1 时刻的估计误差远大于第 k k k 次的测量误差的时候,这时第 k k k 次的估计值就很趋近于测量值 Z k Z_k Zk 了。这个非常好理解,因为你估计的误差大,测量得更加准确,所以就需要去更加信任这个测量值。
而同理,在 k k k 时刻当 e E S T k − 1 ≪ e M E A k {e_{EST_{k-1}} \ll e_{MEA_{k}}} eESTk−1≪eMEAk 时 K k → 0 \color{blue}{K_k} \to 0 Kk→0 , X ^ k = X ^ k − 1 \hat{X}_k = \hat{X}_{k-1} X^k=X^k−1,也就是说当你的测量误差很大的时候,我们去选择相信这个估计值,相信上一次的估计值。
有了上面的知识,我们先来看一个例子,用一个非常简单的卡尔曼滤波器的思想去解决一个问题,它可以分为三步:
Step1:计算 Kalman Gain K k = e E S T k − 1 e E S T k − 1 + e M E A k \color{blue}K_k \color{black}= \frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_{k}}} Kk=eESTk−1+eMEAkeESTk−1
Step2:计算 X ^ k = X ^ k − 1 + K k ( Z k − X ^ k − 1 ) \hat{X}_k = \hat{X}_{k-1} + \color{blue}{K}_k \color{black}(Z_k - \hat{X}_{k-1}) X^k=X^k−1+Kk(Zk−X^k−1)
Step3:更新 e E S T k = ( 1 − K k ) e E S T k − 1 e_{EST_k} = (1 - \color{blue} K_k\color{black})e_{EST_{k-1}} eESTk=(1−Kk)eESTk−1
有了这三步以后,我们就可以去解决一些实际的问题了。比如说还是测量一个物体它的实际长度,比如说是 50mm,假设我们第一次的估计值 X ^ 0 = 40 m m \hat{X}_0 = 40mm X^0=40mm,第一次的估计误差 e E S T 0 = 5 m m e_{EST_0} = 5mm eEST0=5mm,第一次的测量值 Z 1 = 51 m m Z_1 = 51mm Z1=51mm,测量误差是 e M E A k = 3 m m e_{MEA_k} = 3mm eMEAk=3mm,由于使用同样的一个测量工具,所以它第 k k k 次的测量误差也是 3mm
现在可以做一个表格,然后把有的内容填在上面,我们就可以进行递归的计算了
| k k k | Z k Z_k Zk | e M E A k e_{MEA_k} eMEAk | X ^ k \hat{X}_k X^k | K k K_k Kk | e E S T k e_{EST_k} eESTk |
|---|---|---|---|---|---|
| 0 | 40 \color{sienna}40 40 | 5 \color{red}5 5 | |||
| 1 | 51 \color{orange}51 51 | 3 \color{red}3 3 |
当 k = 1 k = 1 k=1 时:
K k = 5 5 + 3 = 0.625 X ^ k = 40 + 0.625 ( 51 − 40 ) = 46.875 e E S T = ( 1 − 0.625 ) 5 = 1.875 \begin{aligned} K_k &= \color{red}\frac{5}{5+3} = \color{green}0.625 \\ \hat{X}_k &= \color{sienna}40 + \color{green}0.625(\color{orange}51 -\color{sienna}40) \color{black}= 46.875 \\ e_{EST} &= (1 - \color{green}0.625)\color{red}5 = 1.875 \end{aligned} KkX^keEST=5+35=0.625=40+0.625(51−40)=46.875=(1−0.625)5=1.875
更新下表格:
| k k k | Z k Z_k Zk | e M E A k e_{MEA_k} eMEAk | X ^ k \hat{X}_k X^k | K k K_k Kk | e E S T k e_{EST_k} eESTk |
|---|---|---|---|---|---|
| 0 | 40 \color{sienna}40 40 | 5 \color{red}5 5 | |||
| 1 | 51 \color{orange}51 51 | 3 \color{red}3 3 | 46.875 46.875 46.875 | 0.625 \color{green}0.625 0.625 | 1.875 1.875 1.875 |
当 k = 2 k = 2 k=2 时:
K k = 1.875 1.875 + 3 = 0.3846 X ^ k = 46.875 + 0.3846 ( 48 − 46.875 ) = 47.308 e E S T = ( 1 − 0.3846 ) 1.875 = 1.154 \begin{aligned} K_k &= \frac{1.875}{1.875+3} = 0.3846 \\ \hat{X}_k &= 46.875 + 0.3846(48-46.875) = 47.308 \\ e_{EST} &= (1 - 0.3846)1.875 = 1.154 \end{aligned} KkX^keEST=1.875+31.875=0.3846=46.875+0.3846(48−46.875)=47.308=(1−0.3846)1.875=1.154
填入到表格中:
| k k k | Z k Z_k Zk | e M E A k e_{MEA_k} eMEAk | X ^ k \hat{X}_k X^k | K k K_k Kk | e E S T k e_{EST_k} eESTk |
|---|---|---|---|---|---|
| 0 | 40 \color{sienna}40 40 | 5 \color{red}5 5 | |||
| 1 | 51 \color{orange}51 51 | 3 \color{red}3 3 | 46.875 46.875 46.875 | 0.625 \color{green}0.625 0.625 | 1.875 1.875 1.875 |
| 2 | 48 48 48 | 3 3 3 | 47.308 47.308 47.308 | 0.3846 0.3846 0.3846 | 1.154 1.154 1.154 |
后面的递归工作我们交给 Python 来做,代码如下:
import matplotlib.pyplot as plte_MEAk = 3
e_ESTk = 5
Xk = [40] + [0]*16
Zk = [51, 48, 47, 52, 51, 48, 49, 53, 48, 49, 52, 53, 51, 52, 49, 50]Kk = 0
for idx in range(len(Zk)):Kk = e_ESTk / (e_ESTk + e_MEAk)Xk[idx + 1] = Xk[idx] + Kk * (Zk[idx] - Xk[idx])e_ESTk = (1 - Kk) * e_ESTkprint(f"第 {idx:2} 次: 卡尔曼增益 = {Kk:.5f}, 估计值 = {Xk[idx + 1]:.5f}, 估计误差 = {e_ESTk:.5f}")k = [i for i in range(17)]
plt.plot(k, Xk, marker='o', color='red', label='Estimates')
plt.plot(k[:-1], Zk, marker = 'o', color='blue', label='Measurements')
plt.xlabel('Times')
plt.ylabel('Value')
plt.title('Kalman Filter Example')
plt.legend(loc='right')plt.savefig("kf.png", bbox_inches='tight', dpi=300)
plt.show()
输出如下:
第 0 次: 卡尔曼增益 = 0.62500, 估计值 = 46.87500, 估计误差 = 1.87500
第 1 次: 卡尔曼增益 = 0.38462, 估计值 = 47.30769, 估计误差 = 1.15385
第 2 次: 卡尔曼增益 = 0.27778, 估计值 = 47.22222, 估计误差 = 0.83333
第 3 次: 卡尔曼增益 = 0.21739, 估计值 = 48.26087, 估计误差 = 0.65217
第 4 次: 卡尔曼增益 = 0.17857, 估计值 = 48.75000, 估计误差 = 0.53571
第 5 次: 卡尔曼增益 = 0.15152, 估计值 = 48.63636, 估计误差 = 0.45455
第 6 次: 卡尔曼增益 = 0.13158, 估计值 = 48.68421, 估计误差 = 0.39474
第 7 次: 卡尔曼增益 = 0.11628, 估计值 = 49.18605, 估计误差 = 0.34884
第 8 次: 卡尔曼增益 = 0.10417, 估计值 = 49.06250, 估计误差 = 0.31250
第 9 次: 卡尔曼增益 = 0.09434, 估计值 = 49.05660, 估计误差 = 0.28302
第 10 次: 卡尔曼增益 = 0.08621, 估计值 = 49.31034, 估计误差 = 0.25862
第 11 次: 卡尔曼增益 = 0.07937, 估计值 = 49.60317, 估计误差 = 0.23810
第 12 次: 卡尔曼增益 = 0.07353, 估计值 = 49.70588, 估计误差 = 0.22059
第 13 次: 卡尔曼增益 = 0.06849, 估计值 = 49.86301, 估计误差 = 0.20548
第 14 次: 卡尔曼增益 = 0.06410, 估计值 = 49.80769, 估计误差 = 0.19231
第 15 次: 卡尔曼增益 = 0.06024, 估计值 = 49.81928, 估计误差 = 0.18072
可视化图如下:

蓝色的是我们的测量结果,红色的是我们一个的估计结果。可以看到我们最开始是从 40 开始的,就是我们初始的估计值,它大概用了五步就到了 49 这个位置,我们之前有说实际值是 50,然后再经过几步的迭代之后,它就越来越靠近我们的实际值。这就是卡尔曼滤波器的一种递归的思想,随着我们不断的去更新,不断的有新的数据进来,它会越来越靠近真实的值。
可以看得出来,这是一个非常简单的利用卡尔曼滤波器的递归思想来做估计的一个例子,我们会在后面的分析中详细展开卡尔曼滤波器的推导过程并给出一些更深层次的应用。
2. 数学基础
这节我们主要讨论四个方面,四个数学基础分别是数据融合(Data Fusion)、协方差矩阵(Covariance Matrix)、状态空间方程(State Space)以及观测器(Observation)
我们先来讨论 Data Fusion 数据融合,还是从一个例子开始,比如说我们用两个称去称一个东西得到了两个结果,分别是 Z 1 = 30 g \color{blue}Z_1=30g Z1=30g Z 2 = 32 g \color{red}Z_2=32g Z2=32g。而且我们知道这两个称都不准,测量都有误差,比如说对于第一个称来说,它的标准差 σ 1 = 2 g \color{blue}\sigma_1=2g σ1=2g 第二个称的标准差 σ 2 = 4 g \color{red}\sigma_2=4g σ2=4g。
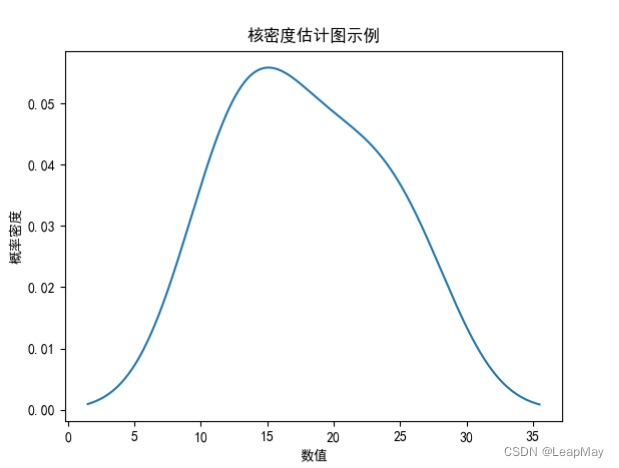
它们都符合正态分布,也叫高斯分布,所以如果说给出这样的一个条件的话,它们在图中表现出来的就是中型的曲线,比如第一个结果的概率分布如下图:

中间的位置是 30g,然后标准差是 2,向左向右各一个标准差就覆盖了 68.4% 的可能性,也就是说测出来的结果在 28g~32g 之间的概率是 68.4%
而对于另外一个,因为它的标准差是 4,所以它的图像更矮一些更胖一些,如下图所示:

关于正态分布和标准差更多细节看观看:【工程数学基础】9_阈值如何选取??在机器视觉中应用正态分布和6-Sigma
我们来把这两个分布绘制在用一张图中,如下图所示:

这个时候我们有了这两个结果,如果让你去根据这两个结果去估算一下,真实值将会是多少呢?🤔
各位看官可以自己思考一下,如果凭感觉的话,它应该是在这两个结果的中间,而且由于第一个称的误差小(即标准差小),所以它会靠近第一个称称出来的结果。
而如果从数学上去找到一个最优的一个估计值我们又该如何做呢?🤔
这就要用到我们上一节介绍过的 Kalman Gain 的这个思想了,可以令这个估计值等于下式:
Z ^ = Z 1 + K ( Z 2 − Z 1 ) \hat{Z} = \color{blue}Z_1 \color{black} + \color{green}K\color{black}(\color{red}Z_2 \color{black}- \color{blue}Z_1\color{black}) Z^=Z1+K(Z2−Z1)
这里面的 K \color{green}K K 就是 Kalman Gain,其值是一个从 0~1 的一个数,可以看出来:
当 K = 0 K = 0 K=0 时, Z ^ = Z 1 \hat{Z} = \color{blue}Z_1 Z^=Z1
当 K = 1 K = 1 K=1 时, Z ^ = Z 2 \hat{Z} = \color{red}Z_2 Z^=Z2
下面就是要去求解 K K K 了,我们的目标就是去求解合适的 K K K 使得 Z ^ \hat{Z} Z^ 这个估计值的标准差最小,也就是方差最小。它的方差计算如下:
σ Z ^ 2 = V a r ( Z ^ ) = V a r ( Z 1 + K ( Z 2 − Z 1 ) ) = V a r ( Z 1 − K Z 1 + K Z 2 ) = V a r ( ( 1 − K ) Z 1 + K Z 2 ) = V a r ( ( 1 − K ) Z 1 ) + V a r ( K Z 2 ) = ( 1 − K ) 2 V a r ( Z 1 ) + K 2 V a r ( Z 2 ) = ( 1 − K ) 2 σ 1 2 + K 2 σ 2 2 \begin{aligned} \sigma^2_{\hat{Z}} &= Var(\hat{Z}) \\ &= Var(Z_1 + K(Z_2-Z_1)) \\ &= Var(Z_1 - KZ_1 + KZ_2) \\ &= Var((1-K)Z_1 + KZ_2) \\ &= Var((1-K)Z_1) + Var(KZ_2) \\ &= (1-K)^2Var(Z_1) + K^2Var(Z_2) \\ &= (1-K)^2\sigma_1^2 + K^2\sigma_2^2 \\ \end{aligned} σZ^2=Var(Z^)=Var(Z1+K(Z2−Z1))=Var(Z1−KZ1+KZ2)=Var((1−K)Z1+KZ2)=Var((1−K)Z1)+Var(KZ2)=(1−K)2Var(Z1)+K2Var(Z2)=(1−K)2σ12+K2σ22
其中 Z 1 Z_1 Z1 和 Z 2 Z_2 Z2 相互独立,我们的目标是要求 σ Z ^ 2 \sigma^2_{\hat{Z}} σZ^2 最小,因此我们可以让它对 K K K 求导,求取其对应的极值,如下:
d σ Z ^ 2 d K = 0 − 2 ( 1 − K ) σ 1 2 + 2 K σ 2 2 = 0 − σ 1 2 + K σ 1 2 + K σ 2 2 = 0 K ( σ 1 2 + σ 2 2 ) = σ 1 2 \begin{aligned} \frac{d\sigma^2_{\hat{Z}}}{dK} &= 0 \\ -2(1-K)\sigma_1^2 + 2K\sigma_2^2 &=0 \\ -\sigma_1^2 + K\sigma_1^2 + K\sigma_2^2 &= 0 \\ K(\sigma_1^2+\sigma_2^2) &= \sigma_1^2 \\ \end{aligned} dKdσZ^2−2(1−K)σ12+2Kσ22−σ12+Kσ12+Kσ22K(σ12+σ22)=0=0=0=σ12
因此最终的 K K K 计算如下:
K = σ 1 2 σ 1 2 + σ 2 2 K = \frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2} K=σ12+σ22σ12
我们把 σ 1 = 2 \sigma_1 = 2 σ1=2 σ 2 = 4 \sigma_2 = 4 σ2=4 代入有
K = σ 1 2 σ 1 2 + σ 2 2 = 2 2 2 2 + 4 2 = 4 4 + 16 = 0.2 K = \frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2} = \frac{2^2}{2^2+4^2}=\frac{4}{4+16}=0.2 K=σ12+σ22σ12=22+4222=4+164=0.2
我们把 K = 0.2 K = 0.2 K=0.2 代入有
Z ^ = Z 1 + K ( Z 2 − Z 1 ) = 30 + 0.2 ( 32 − 30 ) = 30.4 \begin{aligned} \hat{Z} &= \color{blue}Z_1 \color{black} + \color{green}K\color{black}(\color{red}Z_2 \color{black}- \color{blue}Z_1\color{black}) \\ &= \color{blue}30 \color{black} + 0.2 (\color{red}32 \color{black}- \color{blue}30\color{black}) \\ &= 30.4 \end{aligned} Z^=Z1+K(Z2−Z1)=30+0.2(32−30)=30.4
也就是说根据这两个称的特性和测量出来的结果,我们做出了预测,这个预测是 30.4g,并且通过数学证明了它是最优解。这时候也可以去计算它的方差:
σ Z ^ 2 = ( 1 − K ) 2 σ 1 2 + K 2 σ 2 2 = ( 1 − 0.2 ) 2 × 2 2 + 0. 2 2 × 4 2 = 3.2 \begin{aligned} \sigma^2_{\hat{Z}} &= (1-K)^2\sigma_1^2 + K^2\sigma_2^2 \\ &= (1-0.2)^2\times2^2+0.2^2\times4^2 \\ &= 3.2 \end{aligned} σZ^2=(1−K)2σ12+K2σ22=(1−0.2)2×22+0.22×42=3.2
其标准差 σ Z ^ = 3.2 = 1.79 \sigma_{\hat{Z}} = \sqrt{3.2} = 1.79 σZ^=3.2=1.79
所以说我们的这个最优的估计值 σ Z ^ 2 = 30.4 g \sigma^2_{\hat{Z}} = 30.4g σZ^2=30.4g 标准差 σ Z ^ = 1.79 \sigma_{\hat{Z}} = 1.79 σZ^=1.79
如果将它绘制在之前的图中,它应该是一个更高更瘦的图像。如下图所示:

这个过程就叫做数据融合,大家要掌握这个思想,记住这个理念,过一会我们会再回过头来看它。
第二个要聊的就是协方差矩阵 Covariance Matrix,它把方差和协方差在一个矩阵当中表现出来,也就是体现了变量间的一个联动关系。还是从一个例子入手
| 球员 | 身高 | 体重 | 年龄 |
|---|---|---|---|
| 瓦尔迪 | 179 | 74 | 33 |
| 奥巴梅扬 | 187 | 80 | 31 |
| 萨拉赫 | 175 | 71 | 28 |
| Mean | 180.3 | 75 | 30.7 |
上表是 2020 年英超中射手榜前三球员的一些基本的数据,包括身高、体重和年龄。我们将它们当作三个变量分别为 x x x y y y 和 z z z,然后我们求下它们的平均值:
x ˉ = 1 3 ( 179 + 187 + 175 ) = 180.3 y ˉ = 1 3 ( 74 + 80 + 71 ) = 75 z ˉ = 1 3 ( 33 + 31 + 28 ) = 30.7 \begin{aligned} \bar x &= \frac{1}{3}(179+187+175) = 180.3 \\ \bar y &= \frac{1}{3}(74+80+71) = 75 \\ \bar z &= \frac{1}{3}(33+31+28) = 30.7 \end{aligned} xˉyˉzˉ=31(179+187+175)=180.3=31(74+80+71)=75=31(33+31+28)=30.7
分别是身高 180.3,体重 75,年龄 30.7,然后我们还可以计算下它们对应的方差:
σ x 2 = 1 3 ( ( 179 − 180.3 ) 2 + ( 187 − 180.3 ) 2 + ( 175 − 180.3 ) 2 ) = 24.89 σ y 2 = 1 3 ( ( 74 − 75 ) 2 + ( 80 − 75 ) 2 + ( 71 − 75 ) 2 ) = 14 σ z 2 = 1 3 ( ( 33 − 30.7 ) 2 + ( 31 − 30.7 ) 2 + ( 28 − 30.7 ) 2 ) = 4.22 \begin{aligned} \sigma_x^2 &= \frac{1}{3}((179-180.3)^2+(187-180.3)^2+(175-180.3)^2) = 24.89 \\ \sigma_y^2 &= \frac{1}{3}((74-75)^2+(80-75)^2+(71-75)^2) = 14 \\ \sigma_z^2 &= \frac{1}{3}((33-30.7)^2+(31-30.7)^2+(28-30.7)^2) = 4.22 \end{aligned} σx2σy2σz2=31((179−180.3)2+(187−180.3)2+(175−180.3)2)=24.89=31((74−75)2+(80−75)2+(71−75)2)=14=31((33−30.7)2+(31−30.7)2+(28−30.7)2)=4.22
协方差计算如下:
σ x σ y = 1 3 ( ( 179 − 180.3 ) ( 74 − 75 ) + ( 187 − 180.3 ) ( 80 − 75 ) + ( 175 − 180.3 ) ( 71 − 75 ) ) = 18.7 = σ y σ x σ x σ z = 1 3 ( ( 179 − 180.3 ) ( 33 − 30.7 ) + ( 187 − 180.3 ) ( 31 − 30.7 ) + ( 175 − 180.3 ) ( 28 − 30.7 ) ) = 4.4 = σ z σ x σ y σ z = 1 3 ( ( 74 − 75 ) ( 33 − 30.7 ) + ( 80 − 75 ) ( 31 − 30.7 ) + ( 71 − 75 ) ( 28 − 30.7 ) ) = 3.3 = σ z σ y \begin{aligned} \sigma_x \sigma_y &= \frac{1}{3}((179-180.3)(74-75)+(187-180.3)(80-75)+(175-180.3)(71-75)) = 18.7 = \sigma_y \sigma_x\\ \sigma_x \sigma_z &= \frac{1}{3}((179-180.3)(33-30.7)+(187-180.3)(31-30.7)+(175-180.3)(28-30.7)) = 4.4 = \sigma_z \sigma_x \\ \sigma_y \sigma_z &= \frac{1}{3}((74-75)(33-30.7)+(80-75)(31-30.7)+(71-75)(28-30.7)) = 3.3 = \sigma_z \sigma_y \end{aligned} σxσyσxσzσyσz=31((179−180.3)(74−75)+(187−180.3)(80−75)+(175−180.3)(71−75))=18.7=σyσx=31((179−180.3)(33−30.7)+(187−180.3)(31−30.7)+(175−180.3)(28−30.7))=4.4=σzσx=31((74−75)(33−30.7)+(80−75)(31−30.7)+(71−75)(28−30.7))=3.3=σzσy
可以看到如果最后计算出来的值大于 0,则说明两个变量的变化方向是一样的,这时候我们称这两个变量正相关。而如果计算出来的值小于 0,则说明两个变量的变化方向是相反的,这时候我们称这两个变量负相关
然后说到协方差矩阵 P P P,它的形式如下所示:
P = [ σ x 2 σ x σ y σ x σ z σ y σ x σ y 2 σ y σ z σ z σ x σ z σ y σ z 2 ] = [ 24.89 18.7 4.4 18.7 14 3.3 4.4 3.3 4.22 ] P=\begin{bmatrix} \sigma_x^2 & \sigma_x\sigma_y & \sigma_x\sigma_z \\ \sigma_y\sigma_x & \sigma_y^2 & \sigma_y\sigma_z \\ \sigma_z\sigma_x & \sigma_z\sigma_y & \sigma_z^2 \\ \end{bmatrix} =\begin{bmatrix} 24.89 & 18.7 & 4.4 \\ 18.7 & 14 & 3.3 \\ 4.4 & 3.3 & 4.22 \\ \end{bmatrix} P= σx2σyσxσzσxσxσyσy2σzσyσxσzσyσzσz2 = 24.8918.74.418.7143.34.43.34.22
然后我们就可以分析各个数据之间的关系,因为这里只取了三组数据,所以不是非常准确,我们就希望把它扩展一下,在扩展之前我们先来看看如何通过矩阵的运算来计算这个协方差。
这个对于以后要编程的话非常有帮助,我们还是看这个例子,首先我们要先求一个过渡矩阵 a a a
a = [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] − 1 3 [ 1 1 1 1 1 1 1 1 1 ] [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] a=\begin{bmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \\ \end{bmatrix}- \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ \end{bmatrix} \begin{bmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \\ \end{bmatrix} a= x1x2x3y1y2y3z1z2z3 −31 111111111 x1x2x3y1y2y3z1z2z3
协方差矩阵 P P P 的计算则为 P = 1 3 a T a P = \frac{1}{3}a^Ta P=31aTa,通过这样的方法,我们就可以算出协方差矩阵了。
我们现在来分析一下这个协方差矩阵说明了什么,下表中给出了 15 位球员的一个基本信息,它涵盖了五大联赛在 2020 年射手榜的前三位:
| 球员 | 身高 | 体重 | 年龄 |
|---|---|---|---|
| 瓦尔迪 | 179 | 74 | 33 |
| 奥巴梅扬 | 187 | 80 | 31 |
| 萨拉赫 | 175 | 71 | 28 |
| 梅西 | 170 | 72 | 33 |
| 本泽马 | 185 | 81 | 32 |
| 杰拉德 | 177 | 75 | 28 |
| 因莫比莱 | 178 | 71 | 30 |
| C罗 | 187 | 83 | 35 |
| 卢卡库 | 190 | 94 | 27 |
| 姆巴佩 | 178 | 73 | 21 |
| 本耶德尔 | 170 | 68 | 29 |
| 邓贝莱 | 183 | 73 | 23 |
| 莱万多夫斯基 | 184 | 78 | 31 |
| 维尔纳 | 180 | 75 | 24 |
| 桑乔 | 180 | 76 | 30 |
| Mean | 180.2 | 76.27 | 28.3 |
下表则是它们的协方差矩阵:
| 身高 | 体重 | 年龄 | |
|---|---|---|---|
| 身高 | 32.69 | 29.75 | 1.4 |
| 体重 | 29.75 | 38.06 | 3.98 |
| 年龄 | 1.4 | 3.978 | 19.4 |
大家可以仔细观察下,先看协方差矩阵对角线的这几个数,可以看到身高体重的变化还是蛮大的,它们的方差还是很大的。这也就说明了,如果你想成为射手并不会很局限于身高和体重,年龄的跨度也比较大,说明一个射手和年龄的关系也不是特别的大。
接着我们再来看下它们的协方差的关系,首先是身高和体重,可以看到它们的协方差等于 29.75,也就是说明体重和身高是非常的正相关的,随着身高的增加,体重也增加,这是非常非常合理的。然后我们再看年龄和体重和身高,它们的相关性就非常小,一个是 1.4 一个是 3.98,这就说明了对于这些运动员来说,他们的身高、体重和年龄就没有太大的一个关系了,就说明他们确实是保持的还是很好的,并没有因为年龄大了就变胖
最后一个话题就是状态空间的表达式和观测器,其实关于状态空间的表达来说,它是一个完整的体系。现代控制理论就是以状态空间方程为基础的,感兴趣的可参考视频:现代控制理论
在这里我们只是给出一些最基本的一些概念,依然从一个例子入手,一个典型的弹簧振动阻尼系统,如下图所示:

它的质量是 m m m,向右施加的力是 F F F,向右的方向是 x x x,弹簧的胡可系数是 k k k,阻尼系数是 B B B,它的动态方程的表达式如下:
m x ¨ + B x ˙ + k x = F m\ddot{x}+B\dot{x}+kx=F mx¨+Bx˙+kx=F
我们可以把 F F F 定义成 u u u 也就是系统的输入,这个时候如果要把它化成状态空间的一种表达形式,首先就要确定两个状态变量,我们可以令 x 1 = x x_1 = x x1=x x 2 = x ˙ x_2 = \dot{x} x2=x˙,这样的话有
x ˙ 1 = x 2 x ˙ 2 = x ¨ = 1 m u − B m x ˙ − k m x = 1 m u − B m x 2 − k m x 1 \begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= \ddot{x} \\ &= \frac{1}{m}u-\frac{B}{m}\dot{x}-\frac{k}{m}x \\ &= \frac{1}{m}u-\frac{B}{m}x_2-\frac{k}{m}x_1 \end{aligned} x˙1x˙2=x2=x¨=m1u−mBx˙−mkx=m1u−mBx2−mkx1
这样就用两个一阶微分方程把这个形式表达出来了,如果我们这里面还有一个测量量,我们可以把它定义成 z 1 z_1 z1, z 1 z_1 z1 测的是它的位置 z 1 = x = x 1 z_1 = x = x_1 z1=x=x1, z 2 z_2 z2 测的是它的速度 z 2 = x ˙ = x 2 z_2 = \dot{x} = x_2 z2=x˙=x2,这样的话就是一个测量的一个方程。
然后我们可以把上面的四个式子用矩阵的方式把它很紧凑的表达出来,如下所示:
[ x ˙ 1 x ˙ 2 ] = [ 0 1 − k m − B m ] [ x 1 x 2 ] + [ 0 1 m ] u [ z 1 z 2 ] = [ 1 0 0 1 ] [ x 1 x 2 ] \begin{aligned} \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \end{bmatrix} &= \begin{bmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{B}{m} \\ \end{bmatrix} \begin{bmatrix} {x}_1 \\ {x}_2 \\ \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{m} \\ \end{bmatrix} u \\ \\ \begin{bmatrix} z_1 \\ z_2 \\ \end{bmatrix} &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} {x}_1 \\ {x}_2 \\ \end{bmatrix} \end{aligned} [x˙1x˙2][z1z2]=[0−mk1−mB][x1x2]+[0m1]u=[1001][x1x2]
这就是状态空间的表达形式,归纳出来如下所示:
X ˙ ( t ) = A X ( t ) + B U ( t ) Z ( t ) = H X ( t ) \begin{aligned} \dot{X}(t) &= AX(t)+BU(t) \\ Z(t) &= HX(t) \end{aligned} X˙(t)Z(t)=AX(t)+BU(t)=HX(t)
上式是一种连续的表达形式,我们看到 X ˙ ( t ) \dot{X}(t) X˙(t) 就是 X X X 对时间 t t t 的导数,它体现了随时间的变化。如果我们把它写成离散的一种形式,每相隔一个时刻来看这个变化的话,它就可以写成下面的形式:
X k = A X k − 1 + B U k Z k = H X k \begin{aligned} X_k &= AX_{k-1}+BU_{k} \\ Z_k &= HX_k \end{aligned} XkZk=AXk−1+BUk=HXk
这个下标 k k k, k − 1 k-1 k−1, k + 1 k+1 k+1,每一个单位 1 都代表了一个时间单位叫做 sample time,也就是采样时间。这样的话它也代表了一种变化趋势。
当然从连续型到离散型的表达不是直接照抄上面的矩阵结果,是需要根据采样时间来计算的,但这部分内容不是这里所讨论的重点,这里面你只需要理解它的基本概念就可以了。它是体现了一种变化,是从上一步到这一步的一种变化。
好,最后如果大家还记得之前所说的,世界中充满了不确定性。这个时候我们就可以加一些不确定性在里边了。比如说我们的模型也许不准确,加一个 W k − 1 \color{red}W_{k-1} Wk−1 它叫做过程噪音(Process Noise),关于测量我们也可以加上 V k \color{red}V_k Vk 它叫做测量噪音(Measurement Noise),是在测量当中产生的不确定性,那我们整个表达式就变成了下面的形式:
X k = A X k − 1 + B U k + W k − 1 Z k = H X k + V k \begin{aligned} X_k &= AX_{k-1}+BU_{k}\color{red}+W_{k-1} \\ Z_k &= HX_k\color{red}+V_{k} \end{aligned} XkZk=AXk−1+BUk+Wk−1=HXk+Vk
现在我们就有了两个不确定性了,也就是说模型不准确,然后测出来的值也不准确,在这两个都不确定的情况下,如何去估计一个精确的 x ^ k \hat{x}_k x^k 呢?🤔
这就是卡尔曼滤波器需要解决的问题!
大家回想一下我们在开头讲解的数据融合的例子,我们现在遇到的情况其实和上面的那个情况也是差不多的,只不过我们现在有一个不太准的计算结果和一个不太准的测量结果,我们要根据这两个结果来估计一个相对准确的值,来找到一个误差比它们两个本身都要小的一个结果。
这就是我们后面要重点去分析的内容,到此为止,关于 Kalman Filter 的基本理念就讲完了,概念性的直观理解也到此结束了,从之后开始就是比较枯燥的数学推导了,请大家做好准备😄。
结语
本篇博客首先从递归算法出发来理解卡尔曼滤波器,卡尔曼滤波器是一种最优化的、递归的数字处理算法,它更像是一种观测器,而不是一般意义上的滤波器。接着我们讲解了一个实际的例子,利用卡尔曼滤波器的递归思想来估计硬币的直径,随着我们不断地去更新,我们估计的值会越来越接近实际值,这是递归思想的体现。
随后我们讲解了推导卡尔曼滤波器需要的数学基础,包括数据融合、协方差矩阵、状态空间方程和观测器四个部分。我们从两个不准确的称称同一个物体如何获得一个比较准确的结果这个例子出发讲解了数据融合的概念,我们从运动员的身高体重年龄之间的相关性这个例子出发讲解了协方差矩阵的概念,最后我们通过弹簧振动阻尼系统讲解了状态空间表达式的概念。
在下一篇文章中我们将会详细推导卡尔曼增益和误差协方差矩阵,敬请期待😄
参考
- 现代控制理论
- 常用的MarkDown颜色 笔记
- 【卡尔曼滤波器】_Kalman_Filter_全网最详细数学推导【博主强烈推荐!!!👍👍👍】
- 【工程数学基础】9_阈值如何选取??在机器视觉中应用正态分布和6-Sigma
相关文章:

卡尔曼滤波(Kalman Filter)原理浅析-数学理论推导-1
目录 前言数学理论推导1. 递归算法2. 数学基础结语参考 前言 最近项目需求涉及到目标跟踪部分,准备从 DeepSORT 多目标跟踪算法入手。DeepSORT 中涉及的内容有点多,以前也就对其进行了简单的了解,但是真正去做发现总是存在这样或者那样的困惑…...

Linux 文件创建、查看
touch、cat、more命令 ①touch命令——创建文件 ②cat命令——查看文件内容全部显示 这是txt.txt文件内容 使用cat命令查看 ③more命令——查看文件内容支持翻页 在查看的过程中,通过空格翻页,通过q退出查看...
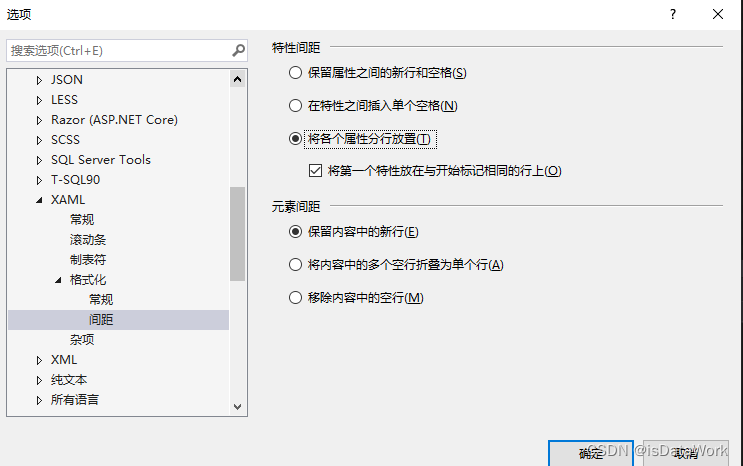
WPF 如何让xmal的属性换行显示 格式化
WPF 如何让UI的xmal 按照下面的格式化显示 首先格式化显示在VS中的快捷键是 Ctrl KD 然后需要配置,工具 选项 -文本编辑器 -xmal -格式化-间距 更改成如下就可以了...

Linux学习之MySQL主从复制
MySQL配置一主一从 环境准备: 两台服务器: Master:192.168.88.53,Slave:192.168.88.54 在两台服务器上安装mysql-server # 配置主服务器192.168.88.53 # 启用binlog日志 [rootmysql53 ~]# yum -y install mysql-ser…...
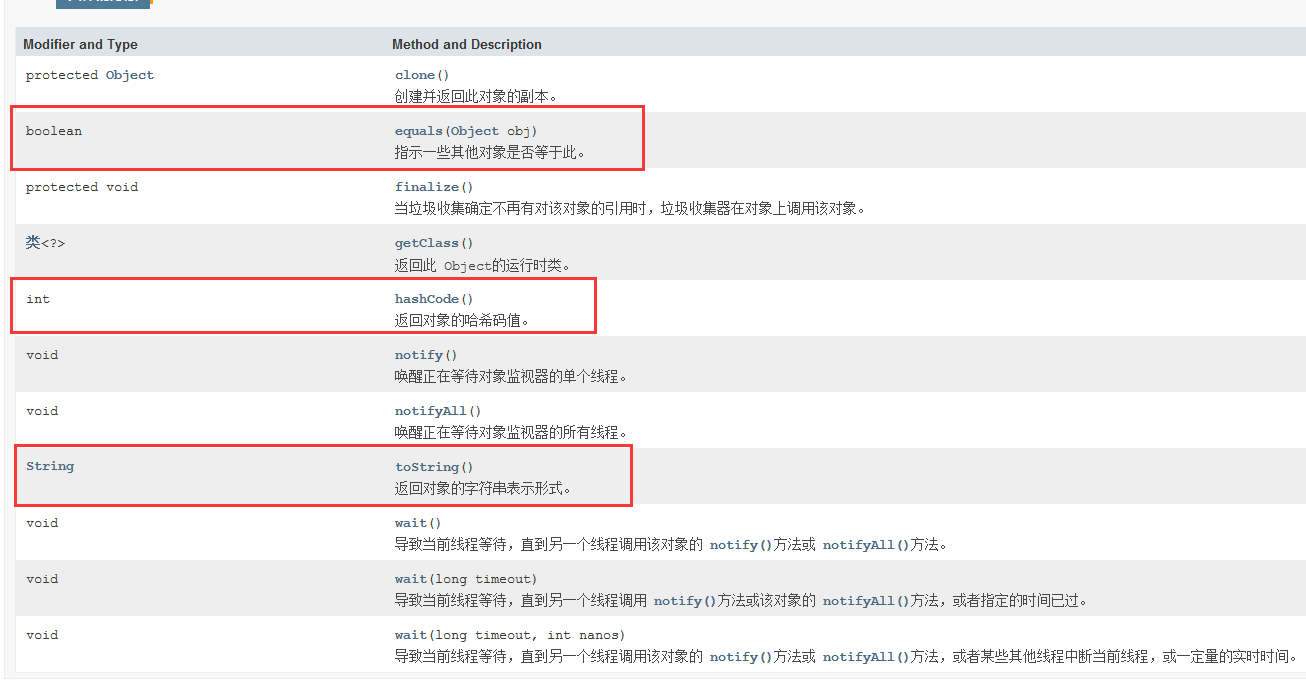
【JavaSE笔记】抽象类与接口
一、抽象类 1、概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。 package demo2…...
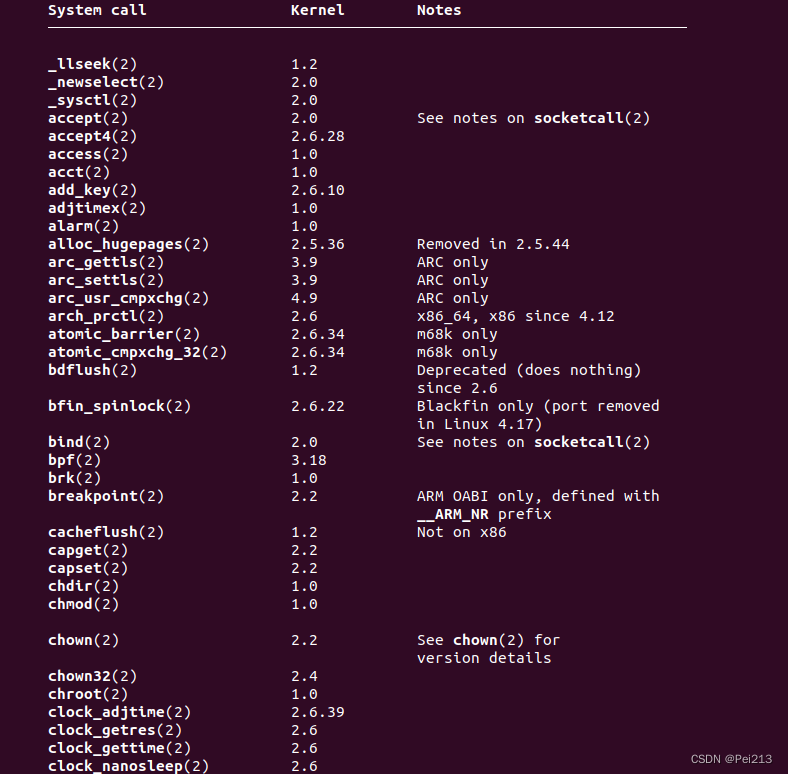
详谈操作系统中的内核态和用户态
不知道大家有没有思考过这样一个问题:什么是处理器(CPU)的状态?🤔 其实CPU和人一样,没有执行程序的时候,是没有什么状态的,当它执行的程序是用户程序的时候就叫用户态,当执行的程序是操作系统的代码时就叫系统态或者内…...

OpenWrt KernelPackage分析
一. 前言 KernelPackage是OpenWrt用来编译内核模块的函数,其实KernelPackage后面会调用BuildPackage,这里会一块将BuildPackage也顺便分析,本文以gpio-button-hotplug驱动模块为例,讲解整个编译过程。 gpio-button-hotplug驱动编译…...
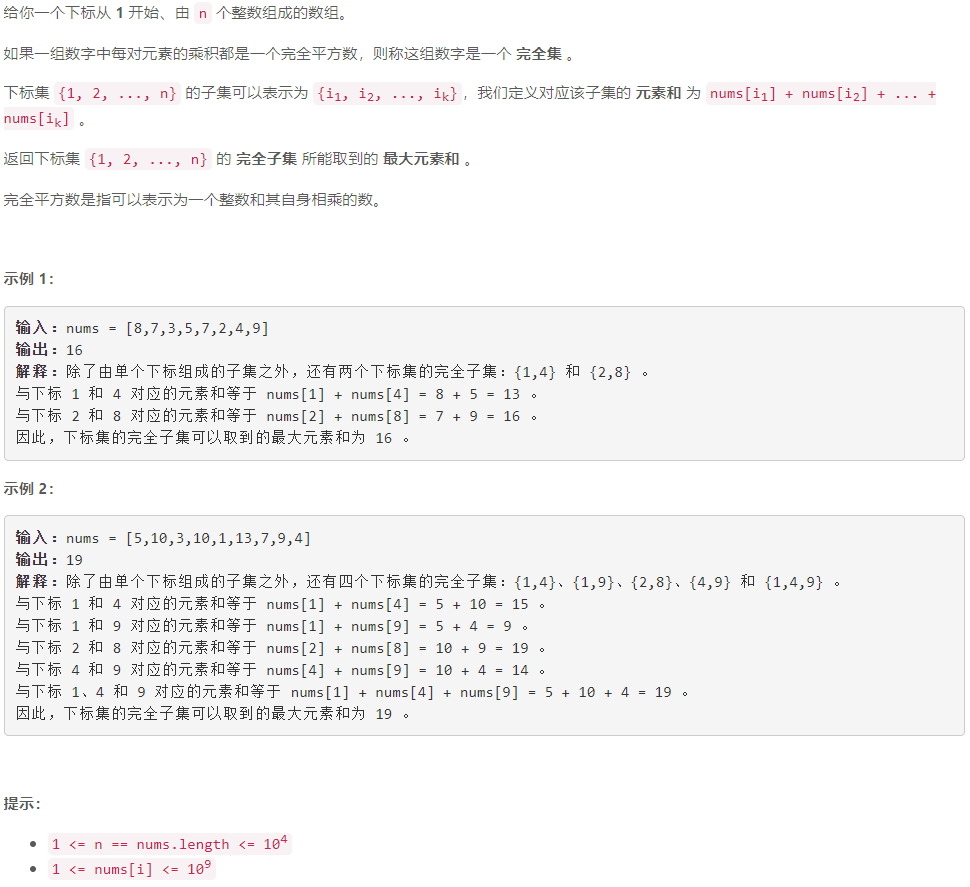
第 363 场 LeetCode 周赛题解
A 计算 K 置位下标对应元素的和 模拟 class Solution { public:int pop_cnt(int x) {//求x的二进制表示中的1的位数int res 0;for (; x; x >> 1)if (x & 1)res;return res;}int sumIndicesWithKSetBits(vector<int> &nums, int k) {int res 0;for (int i…...

ffplay源码解析-main入口函数
main入口函数 初始化 变量、缓存区、SDL窗口初始化等 int main(int argc, char **argv) {int flags;VideoState *is; // av_log_set_level(AV_LOG_TRACE);init_dynload();av_log_set_flags(AV_LOG_SKIP_REPEATED);parse_loglevel(argc, argv, options);/// av_log_set_le…...

这些Coding套路你不会还不知道吧?
对于一名程序员来说,编码进阶是成为优秀工程师非常重要的一步,它可以让我们更加熟练地掌握编程,深入理解数据结构和算法,从而更好地完成复杂的任务,提高工作效率。而我认为熟练使用设计模式就是编码进阶的最好方式之一…...

Spring Boot深度解析:快速开发的秘密
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
)
mysql数据库备份(mysqldump)
mysqldump命令备份数据 mysqldump -u root -p --databases 数据库1 数据库2 > xxx.sqlmysqldump常用操作示例 1. 备份全部数据库的数据和结构 mysqldump -uroot -p123456 -A > /data/mysqlbackup/mydb.sql2. 备份全部数据库的结构(加 -d 参数) …...
linux Nginx+Tomcat负载均衡、动静分离
linux NginxTomcat负载均衡、动静分离 1、Tomcat的基本介绍1.1Tomcat是什么?1.2Tomcat的构成组件1.3Tomcat的核心功能1.4Tomcat请求过程 2、Tomcat部署2.1安装tomcat2.2优化tomcat启动速度2.4主要目录说明 3、Tomcat 虚拟主机配置3.1创建fsj和mws项目目录和文件3.2修…...
ts 枚举类型原理及其应用详解
ts 枚举类型介绍 TypeScript的枚举类型是一种特殊的数据类型,它允许开发者为一组相关值定义一个共同的名称,使我们可以更清晰、更一致地使用这些值。 枚举类型在TypeScript中用enum关键字定义,每个枚举值默认都是数字类型,从0开…...
腾讯mini项目-【指标监控服务重构】2023-08-23
今日已办 进度和问题汇总 请求合并 feature/venus tracefeature/venus metricfeature/profile-otel-baserunner-stylebugfix/profile-logger-Syncfeature/profile_otelclient_enable_config 完成otel 开关 trace-采样metrice-reader 已经都在各自服务器运行,并接入…...

C- ssize_t size_t
size_t 和 ssize_t 都是在 C 和 C 的标准库中定义的数据类型,它们通常用于表示大小和长度。然而,它们有关键的区别。 size_t: 定义:size_t 是一个无符号整数类型,它是适合表示对象的大小的类型。在 POSIX 中,它也用于…...

ubuntu20.04 Supervisor 开机自启动脚本一文配置
前言: 最近发现一种非常好的开机启动服务方式,不光可以开机自启动,而且还可以进行开机节点的进程守护,这样大大确保了线程的稳定情况,这种服务甚至可以守护开机的进程,所以比之前设置 rc.local 开机自启动脚本一文配置节点好出很多,它甚至可以使用网页登录监管我开机自启…...

【面试刷题】——函数指针和指针函数
“函数指针”(function pointer)和 “指针函数”(pointer to function)是两个不同的概念,它们涉及到指针和函数的结合使用。 函数指针(Function Pointer): 函数指针是指向函数的指…...
目标分类笔记(一): 利用包含多个网络多种训练策略的框架来完成多目标分类任务(从数据准备到训练测试部署的完整流程)
目标分类 一、目标分类介绍1.1 二分类和多分类的区别1.2 单标签和多标签输出的区别 二、代码获取三、数据集准备四、环境搭建4.1 环境测试 五、模型训练六、模型测试6.1 多标签训练-单标签输出结果6.2 多标签训练-多标签输出结果 一、目标分类介绍 目标分类是一种监督学习任务…...
【100天精通Python】Day61:Python 数据分析_Pandas可视化功能:绘制饼图,箱线图,散点图,散点图矩阵,热力图,面积图等(示例+代码)
目录 1 Pandas 可视化功能 2 Pandas绘图实例 2.1 绘制线图 2.2 绘制柱状图 2.3 绘制随机散点图 2.4 绘制饼图 2.5 绘制箱线图A 2.6 绘制箱线图B 2.7 绘制散点图矩阵 2.8 绘制面积图 2.9 绘制热力图 2.10 绘制核密度估计图 1 Pandas 可视化功能 pandas是一个强大的数…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
