最小二乘法
Least Square Method
- 1、相关的矩阵公式
- 2、线性回归
- 3、最小二乘法
- 3.1、损失函数(Loss Function)
- 3.2、多维空间的损失函数
- 3.3、解析法求解
- 3.4、梯度下降法求解
1、相关的矩阵公式
P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ = A T i i : σ ξ T A ξ σ ξ = A T ξ + A ξ i i i : ( A B ) T = B T A T i v : ( A + B ) T = A T + B T v : ∥ ξ ∥ = ξ T ξ \begin{array}{l} Precondit{\rm{i}}on:\xi \in {R^n},A \in {R^{n*n}}\\ \\ i:\frac{{\sigma A\xi }}{{\sigma \xi }} = {A^T}\\ \\ ii:\frac{{\sigma {\xi ^T}A\xi }}{{\sigma \xi }} = {A^T}\xi + A\xi \\ \\ iii:{\left( {AB} \right)^T} = {B^T}{A^T}\\ \\ iv:{\left( {A + B} \right)^T} = {A^T} + {B^T}\\ \\ v:\left\| \xi \right\| = {\xi ^T}\xi \end{array} Precondition:ξ∈Rn,A∈Rn∗ni:σξσAξ=ATii:σξσξTAξ=ATξ+Aξiii:(AB)T=BTATiv:(A+B)T=AT+BTv:∥ξ∥=ξTξ
2、线性回归
线性回归(Linear Regression)个人理解大概是说,一组数据基本上服从线性分布。举一个在二维平面中线性回归的例子,如下图所示,我们可以找到一条表达式为 y = a x + b y=ax+b y=ax+b的直线来大概的拟合这些数据。进而,我们可以用这条直线去预测新输入的点的相应的坐标。那么这种寻找线性方程去拟合数据的方式我们称之为线性回归。

3、最小二乘法
3.1、损失函数(Loss Function)
在二维平面中,我们可以设这条可以拟合大多数数据的直线的表达式如下:
h ( θ ) = θ 1 x + θ 2 h\left( \theta \right) = {\theta _1}{x} + {\theta _2} h(θ)=θ1x+θ2
其中 θ 1 {{\theta _1}} θ1和 θ 2 {{\theta _2}} θ2就是 y = a x + b y = ax + b y=ax+b中的 a a a和 b b b,只是换了一种表达而已。
接着,可以求得平面上每一个点在这条直线上对应的坐标(即估计值):
h 1 ( θ ) = θ 1 x 1 + θ 2 h 2 ( θ ) = θ 1 x 2 + θ 2 . . . . h n ( θ ) = θ 1 x n + θ 2 \begin{array}{l} {h_1}\left( \theta \right) = {\theta _1}{x_1} + {\theta _2}\\ {h_2}\left( \theta \right) = {\theta _1}{x_2} + {\theta _2}\\ ....\\ {h_n}\left( \theta \right) = {\theta _1}{x_n} + {\theta _2} \end{array} h1(θ)=θ1x1+θ2h2(θ)=θ1x2+θ2....hn(θ)=θ1xn+θ2
再求这些点在直线上的坐标和真实坐标的差的平方,就得到损失函数的表达式。
L ( θ ) = ∑ i = 1 m ( h i ( θ ) − f ( x i ) ) 2 L\left( \theta \right) = \sum\limits_{i = 1}^m {{{\left( {{h_i}\left( \theta \right) - f\left( {{x_i}} \right)} \right)}^2}} L(θ)=i=1∑m(hi(θ)−f(xi))2
其中 f ( x i ) {f\left( {{x_i}} \right)} f(xi)则是 x i {{x_i}} xi对应的真实坐标值。
因此,可以通过损失函数 L ( θ ) L\left( \theta \right) L(θ)来找出适当的 θ 1 {{\theta _1}} θ1和 θ 2 {{\theta _2}} θ2,使其 f ( x i ) {f\left( {{x_i}} \right)} f(xi)之间的方差最小。求解方法放在后面讲。
3.2、多维空间的损失函数
在 m m m维线性空间中,有 n n n个点。其对应的预测方程应该如下:
h 1 ( θ ) = θ 1 x 11 + θ 2 x 12 + . . . + θ m − 1 x 1 m − 1 + θ m h 2 ( θ ) = θ 1 x 21 + θ 2 x 22 + . . . + θ m − 1 x 2 m − 1 + θ m . . . h n ( θ ) = θ 1 x n 1 + θ 2 x n 2 + . . . + θ m − 1 x n m − 1 + θ m \begin{array}{l} {h_1}\left( \theta \right) = {\theta _1}{x_{11}} + {\theta _2}{x_{12}} + ... + {\theta _{m - 1}}{x_{1m - 1}} + {\theta _m}\\ {h_2}\left( \theta \right) = {\theta _1}{x_{21}} + {\theta _2}{x_{22}} + ... + {\theta _{m - 1}}{x_{2m - 1}} + {\theta _m}\\ ...\\ {h_n}\left( \theta \right) = {\theta _1}{x_{n1}} + {\theta _2}{x_{n2}} + ... + {\theta _{m - 1}}{x_{nm - 1}} + {\theta _m} \end{array} h1(θ)=θ1x11+θ2x12+...+θm−1x1m−1+θmh2(θ)=θ1x21+θ2x22+...+θm−1x2m−1+θm...hn(θ)=θ1xn1+θ2xn2+...+θm−1xnm−1+θm
其中 n > m n>m n>m(方程数量等比未知数多才能有解)。损失函数的表达式依旧如此:
L ( θ ) = ∑ i = 1 m ( h i ( θ ) − f ( x i ) ) 2 L\left( \theta \right) = \sum\limits_{i = 1}^m {{{\left( {{h_i}\left( \theta \right) - f\left( {{x_i}} \right)} \right)}^2}} L(θ)=i=1∑m(hi(θ)−f(xi))2
那么再将以上的所有变量矩阵化:

可以得到损失函数的表达式为:
L ( θ ) = ∥ X θ − F ∥ 2 = ( X θ − F ) T ( X θ − F ) L\left( \theta \right) = {\left\| {X\theta - F} \right\|^2} = {\left( {X\theta - F} \right)^T}\left( {X\theta - F} \right) L(θ)=∥Xθ−F∥2=(Xθ−F)T(Xθ−F)
再展开化简:
L ( θ ) = ∥ X θ − F ∥ 2 = ( X θ − F ) T ( X θ − F ) = ( θ T X T − F T ) ( X θ − F ) = θ T X T X θ − θ T X T F − F T X θ + F T F = θ T X T X θ − 2 F T X θ + F T F \begin{array}{l} L\left( \theta \right) = {\left\| {X\theta - F} \right\|^2} = {\left( {X\theta - F} \right)^T}\left( {X\theta - F} \right)\\ \\ = \left( {{\theta ^T}{X^T} - {F^T}} \right)\left( {X\theta - F} \right) = {\theta ^T}{X^T}X\theta - {\theta ^T}{X^T}F - {F^T}X\theta + {F^T}F\\ \\ = {\theta ^T}{X^T}X\theta - 2{F^T}X\theta + {F^T}F \end{array} L(θ)=∥Xθ−F∥2=(Xθ−F)T(Xθ−F)=(θTXT−FT)(Xθ−F)=θTXTXθ−θTXTF−FTXθ+FTF=θTXTXθ−2FTXθ+FTF
根据上文,我们知道化简的目的是为了找到适当的 θ \theta θ使得损失函数 L ( θ ) L\left( \theta \right) L(θ)最小,而常用的求 θ \theta θ有两种,分别是解析法求解和梯度下降法。
3.3、解析法求解
从高数可以知,当偏导等于零时,该点是极值点(说的不严谨emm)。所以我们直接求偏导,另其为零即可得 θ \theta θ。
σ L ( θ ) σ θ = 2 X T X θ − 2 X T F = 0 θ = ( X T X ) − 1 X T F \begin{array}{l} \frac{{\sigma L\left( \theta \right)}}{{\sigma \theta }} = 2{X^T}X\theta - 2{X^T}F = 0\\ \\ \theta = {\left( {{X^T}X} \right)^{ - 1}}{X^T}F \end{array} σθσL(θ)=2XTXθ−2XTF=0θ=(XTX)−1XTF
但这种方法要求 X T X {{{X^T}X}} XTX是可逆的,即行列式不为零or满秩。很多时候这个条件并不成立,所以在机器学习(Machine Learning)中经常用到梯度下降法。
3.4、梯度下降法求解
梯度下降基本思想是先随便取一个 θ i {\theta _i} θi,然后带入下式看看损失函数多大,然后再在 θ i {\theta _i} θi基础上,取一个稍微小一点或大一点的 θ j {\theta _j} θj带入下式,看看此时的损失函数多大。如此往复,找到那个最优的 θ \theta θ的取值。
L ( θ i ) = θ i T X T X θ i − 2 F T X θ i + F T F L\left( {{\theta _{\rm{i}}}} \right) = {\theta _i}^T{X^T}X{\theta _i} - 2{F^T}X{\theta _i} + {F^T}F L(θi)=θiTXTXθi−2FTXθi+FTF
相关文章:

最小二乘法
Least Square Method 1、相关的矩阵公式2、线性回归3、最小二乘法3.1、损失函数(Loss Function)3.2、多维空间的损失函数3.3、解析法求解3.4、梯度下降法求解 1、相关的矩阵公式 P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ…...

使用stelnet进行安全的远程管理
1. telnet有哪些不足? 2.ssh如何保证数据传输安全? 需求:远程telnet管理设备 用户定义需要在AAA模式下: 开启远程登录的服务:定义vty接口 然后从R2登录:是可以登录的 同理R3登录: 在R1也可以查…...

python 二手车数据分析以及价格预测
二手车交易信息爬取、数据分析以及交易价格预测 引言一、数据爬取1.1 解析数据1.2 编写代码爬1.2.1 获取详细信息1.2.2 数据处理 二、数据分析2.1 统计分析2.2 可视化分析 三、价格预测3.1 价格趋势分析(特征分析)3.2 价格预测 引言 本文着眼于车辆信息,结合当下较…...
JAVA医药进销存管理系统(附源码+调试)
JAVA医药进销存管理系统 功能描述 (1)登录模块:登录信息等存储在数据库中 (2)基本信息模块:分为药品信息模块、客户情况模块、供应商情况模块; (3)业务管理模块&#x…...

H5 <blockquote> 标签
主要应用于:内容引用 标签定义及使用说明 <blockquote> 标签定义摘自另一个源的块引用。 浏览器通常会对 <blockquote> 元素进行缩进。 提示和注释 提示:如果标记是不需要段落分隔的短引用,请使用 <q>。 HTML 4.01 与 H…...
nginx配置指南
nginx.conf配置 找到Nginx的安装目录下的nginx.conf文件,该文件负责Nginx的基础功能配置。 配置文件概述 Nginx的主配置文件(conf/nginx.conf)按以下结构组织: 配置块功能描述全局块与Nginx运行相关的全局设置events块与网络连接有关的设置http块代理…...

【数据结构】优先级队列(堆)
文章目录 💐1. 优先级队列1.1 概念 💐2.堆的概念及存储方式2.1 什么是堆2.2 为什么要用完全二叉树描述堆呢?2.3 为什么说堆是在完全二叉树的基础上进行的调整?2.4 使用数组还原完全二叉树 💐3. 堆的常用操作-模拟实现3…...
前端笔试2
1.下面哪一个是检验对象是否有一个以自身定义的属性? foo.hasOwnProperty("bar")bar in foo foo["bar"] ! undefinedfoo.bar ! null 解析: bar in foo 检查 foo 对象是否包含名为 bar 的属性,但是这个属性可以是从原型链继承来的&a…...

LeetCode:66.加一
66.加一 来源:力扣(LeetCode) 链接: https://leetcode.cn/problems/plus-one/description/ 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数…...

Redis 常用命令
目录 全局命令 1)keys 2)exists 3) del(delete) 4)expire 5)type SET命令 GET命令 MSET 和 MGET命令 其他SET命令 计数命令 redis-cli,进入redis 最核心的命令:我们这里只是先介绍 set 和 get 最简单的操作…...
用于字符和字符串的区别)
Integer.valueOf()用于字符和字符串的区别
LeetCode 17 电话号码的字母组合 先贴代码 class Solution {List<String> result new ArrayList<>();String temp new String("");Integer num;public List<String> letterCombinations(String digits) {dfs(digits, 0);return result;} publi…...
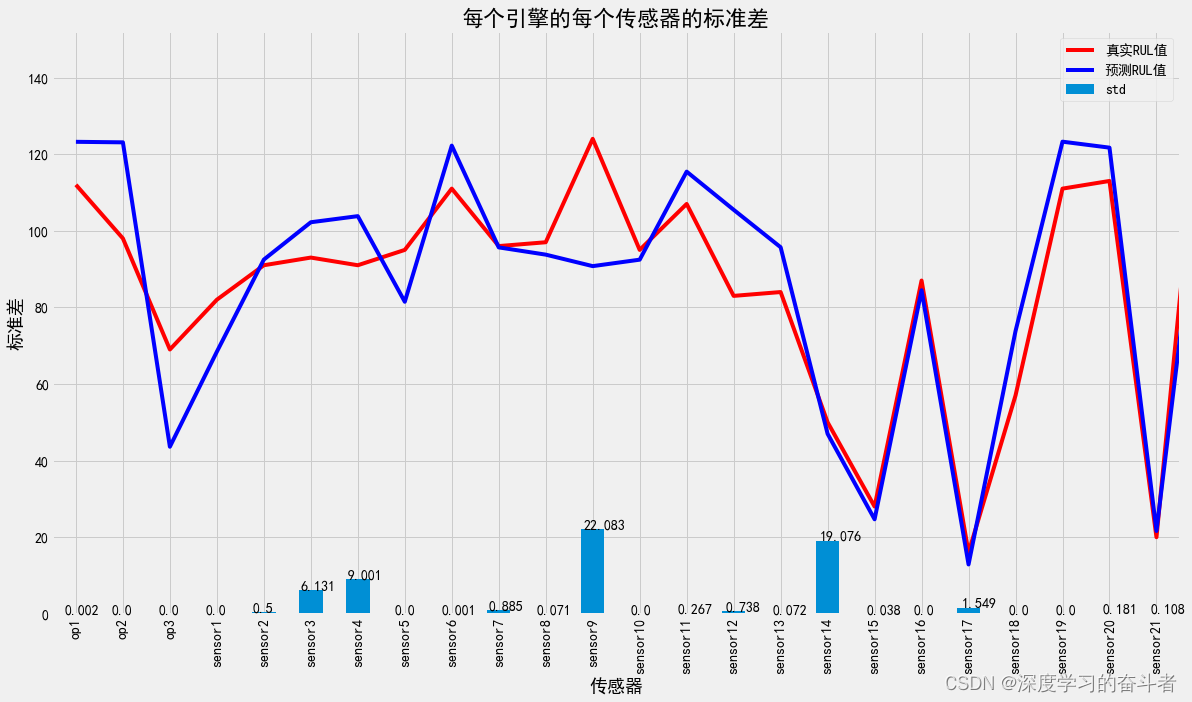
机械寿命预测(基于NASA C-MAPSS数据的剩余使用寿命RUL预测,Python代码,CNN_LSTM模型,有详细中文注释)
1.效果视频:机械寿命预测(NASA涡轮风扇发动机剩余使用寿命RUL预测,Python代码,CNN_LSTM模型,有详细中文注释)_哔哩哔哩_bilibili 环境库版本: 2.数据来源:https://www.nasa.gov/int…...
ConfigMaps-1
文章目录 主要内容一.使用 YAML 文件创建1.在data节点创建了一些键值:代码如下(示例): 2.解释 二.使用命令行创建1.创建了一个名为 person 的键值:代码如下(示例): 2.解释3.创建了一个 index.html 文件&…...

docker上安装es
安装docker 1 安装docker依赖 yum install -y yum-utils2 设置docker仓库镜像地址 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo3 安装制定版本的docker yum -y install docker-ce-20.10.17-3.el74 查看是否安装成功 y…...
#循循渐进学51单片机#c语言基础和流水灯实现#not.3
1、熟练掌握二进制、十进制和十六进制的转换方法。 多少进制就是多少之间相加,比如十六进制就是十六一次一加;二进制转化十六进制,分成四个一组。 2、C语言变量类型与取值范围,for、while等基本语句的用法。 for、while等基本语句…...
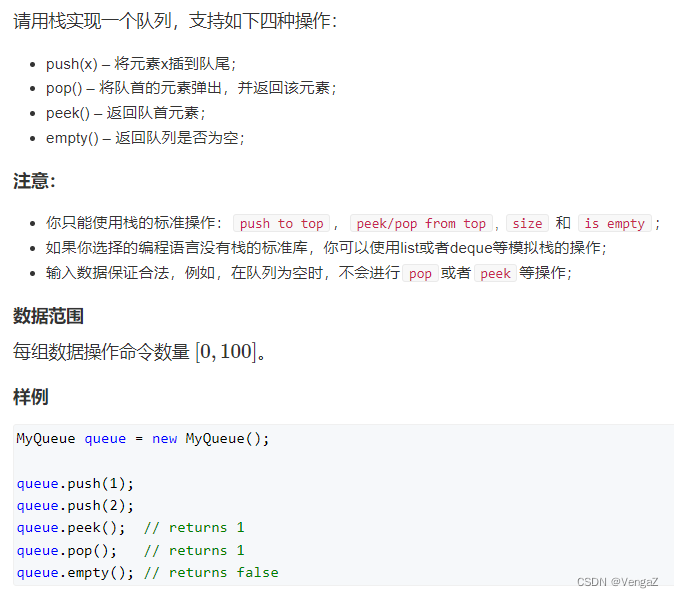
算法刷题 week3
这里写目录标题 1.重建二叉树题目题解(递归) O(n) 2.二叉树的下一个节点题目题解(模拟) O(h) 3.用两个栈实现队列题目题解(栈,队列) O(n) 1.重建二叉树 题目 题解 (递归) O(n) 递归建立整棵二叉树:先递归创建左右子树,然后创建根节点&…...
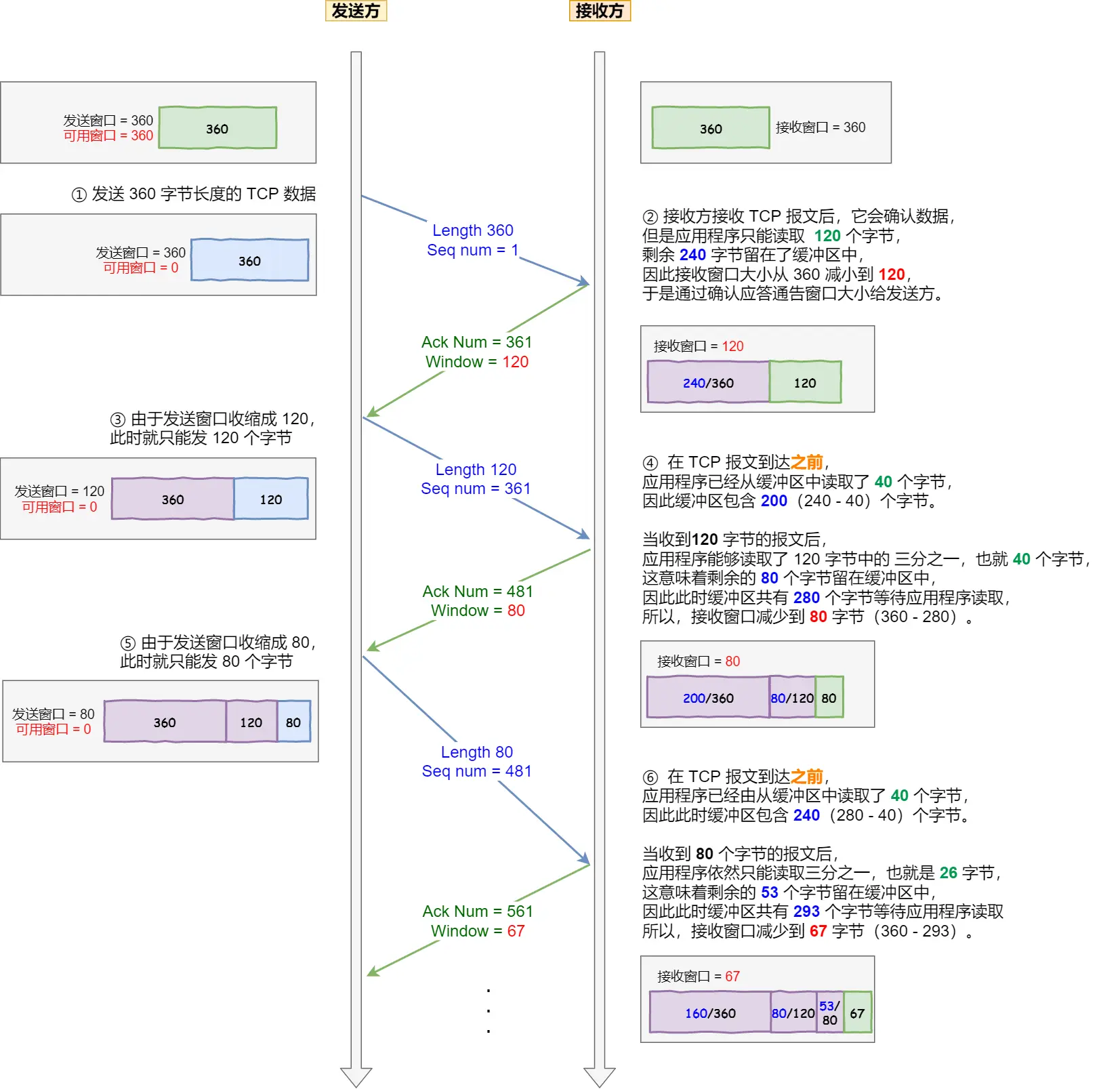
TCP详解之流量控制
TCP详解之流量控制 发送方不能无脑的发数据给接收方,要考虑接收方处理能力。 如果一直无脑的发数据给对方,但对方处理不过来,那么就会导致触发重发机制,从而导致网络流量的无端的浪费。 为了解决这种现象发生,TCP 提…...

mac根目录下创建文件不能问题
mac根目录下创建文件不能问题 解决办法2: 原因 mac os引入了系统完整性保护(SIP)机制,无法在/、/usr目录下新建文件 解决办法1: 打开终端,输入 csrutil status显示enabled表示启用了SIP,接下来需要禁用SIP…...

stable diffusion model训练遇到的问题【No module named ‘triton‘】
一天早晨过来,发现昨天还能跑的diffusion代码,突然出现了【No module named ‘triton’】的问题,导致本就不富裕的显存和优化速度雪上加霜,因此好好探究了解决方案。 首先是原因,由于早晨过来发现【电脑重启】导致了【…...

线性dp,优化记录,273. 分级
273. 分级 273. 分级 - AcWing题库 给定长度为 N 的序列 A,构造一个长度为 N 的序列 B,满足: B 非严格单调,即 B1≤B2≤…≤BN 或 B1≥B2≥…≥BN。最小化 S∑Ni1|Ai−Bi|。 只需要求出这个最小值 S。 输入格式 第一行包含一…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
