面试算法4:只出现一次的数字
题目
输入一个整数数组,数组中只有一个数字出现了一次,而其他数字都出现了3次。请找出那个只出现一次的数字。例如,如果输入的数组为[0,1,0,1,0,1,100],则只出现一次的数字是100。
分析
这个题目有一个简化版的类似的题目“输入数组中除一个数字只出现一次之外其他数字都出现两次,请找出只出现一次的数字”。任何一个数字异或它自己的结果都是0。如果将数组中所有数字进行异或运算,那么最终的结果就是那个只出现一次的数字。
在这个题目中只有一个数字出现了一次,其他数字出现了3次。相同的3个数字异或的结果是数字本身,但是将数组中所有数字进行异或运算并不能消除出现3次的数字。因此,需要想其他办法。
一个整数是由32个0或1组成的。我们可以将数组中所有数字的同一位置的数位相加。如果将出现3次的数字单独拿出来,那么这些出现了3次的数字的任意第i个数位之和都能被3整除。因此,如果数组中所有数字的第i个数位相加之和能被3整除,那么只出现一次的数字的第i个数位一定是0;如果数组中所有数字的第i个数位相加之和被3除余1,那么只出现一次的数字的第i个数位一定是1。这样只出现一次的任意第i个数位可以由数组中所有数字的第i个数位之和推算出来。当我们知道一个整数任意一位是0还是1之后,就可以知道它的数值。
解
public class Test {public static void main(String[] args) {int[] nums = {0, 1, 0, 1, 0, 1, 100};int result = singleNumber(nums);System.out.println(result);}public static int singleNumber(int[] nums) {int[] bitSums = new int[32];for (int num : nums) {for (int i = 0; i < 32; i++) {bitSums[i] += (num >> (31 - i)) & 1;}}int result = 0;for (int i = 0; i < 32; i++) {result = (result << 1) + bitSums[i] % 3;}return result;}
}
相关文章:

面试算法4:只出现一次的数字
题目 输入一个整数数组,数组中只有一个数字出现了一次,而其他数字都出现了3次。请找出那个只出现一次的数字。例如,如果输入的数组为[0,1,0,1,0,1,100],则只…...

#与##的用法
# 作用: 左右加双引号,使其变成字符串 #的作用:是在形参左右各加双引号,使它变成字符串。#define STR(param) #paramchar *pStr STR(hello); // 展开后 char *pStr “hello”; ## 作用:胶水,使…...

Flutter的路由router-页面跳转
文章目录 概念介绍基本路由(Basic Routing)跳转到某个页面弹出页面 命名路由(Named Routing)第三方路由管理库(Third-Party Routing Libraries) Android原生的路由Intent-based Routing(基于Int…...

24v转5v稳压芯片-5A大电流输出ic
这款24V转5V5A汽车充电芯片具有以下特性和参数: - 宽输入电压范围:4.5V至36V - 最大输出电流:5.0A - 高达92%的转换效率 - 恒流/恒压模式控制 - 最大占空比100% - 可调输出电压 - 2%的输出电压精度 - 集成40mΩ高侧开关 - 集成18mΩ低侧开关 …...
(06))
Layui + Flask | 表单元素(组件篇)(06)
表单元素是输入框、选择框、复选框、开关、单选框等表单项组件,用于对表单域进行输入。layui 的表单元素对原生的表单元素进行了大幅的用着,有好看的 UI 同时又有非常方便操作的 API。 输入框 https://layui.dev/docs/2.8/form/input.html 输入框组件是对文本框 <input ty…...
Kakfa - Producer机制原理与调优
Producer是Kakfa模型中生产者组件,也就是Kafka架构中数据的生产来源,虽然其整体是比较简单的组件,但依然有很多细节需要细品一番。比如Kafka的Producer实现原理是什么,怎么发送的消息?IO通讯模型是什么?在实…...
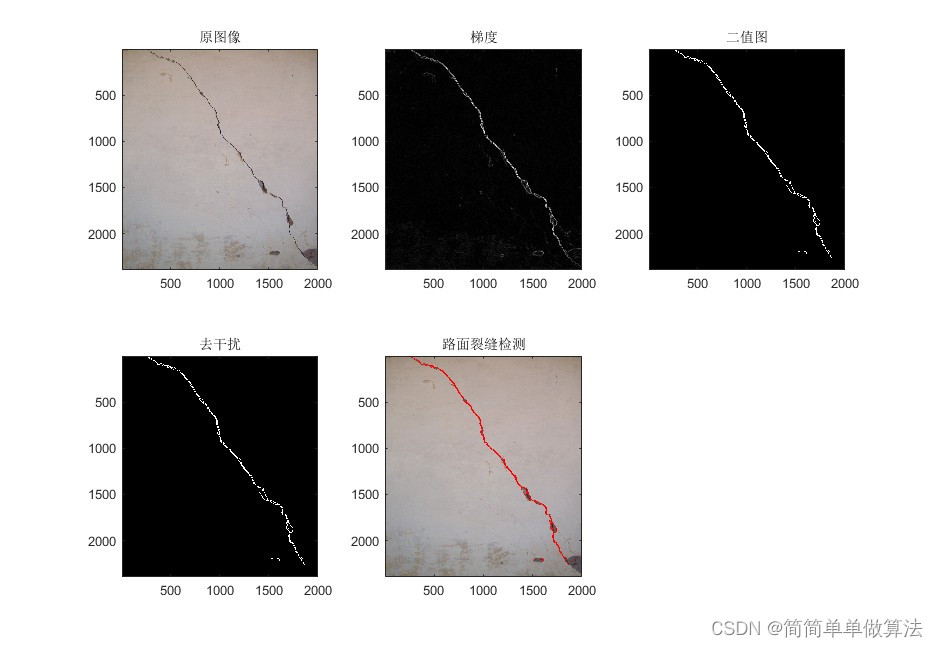
基于图像形态学处理和边缘提取算法的路面裂痕检测matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 [Rr,Cc] size(Image1);% 获取 Image1 矩阵的大小(行数和列数) % 创…...
opencv 基础(持续更新中)
1 前言 https://www.couragesteak.com/ 2 安装 3 基础属性demo 打开一张图片: import cv2img cv2.imread(./girl.jpg)print(img.shape) # (1536, 1024, 3) 数组形状 print(type(img)) # numpy 数组 print(img) # 三维数组(彩色图片&am…...

科普现场!万博智云参加第五届张江汇智科普节
9月15日,第五届张江汇智科普节在汇智国际商业中心如期开展,展会中汇集了众多信息科技领域的新兴产品,展示内容主要分为国产替代和元宇宙场景展示两个方面。展现国产化最新科技成果,践行技术普惠理念,把高、精、专的技术…...
并记录过程产生的BUG问题。)
【记录】实现从Linux下载下载文件(文件导出功能)并记录过程产生的BUG问题。
前言 导出功能的实现,主要记录总结导出过程中出现的一些问题。 代码实现导出功能 public R templateDown(HttpServletResponse response) {String fileName "template.xlsx";// 清空responseresponse.reset();response.setCharacterEncoding("UTF…...

可扩展性表设计方案
文章目录 1 使用预留字段2 使用JSON字段3 使用单表继承4 构建属性表5 直接构建新表6 适当冗余 1 使用预留字段 在表设计初期,可以预留一些命名通用的备用字段,例如field1、field2、field3。当业务需要增加新字段时,就直接使用这些预留字段,无…...
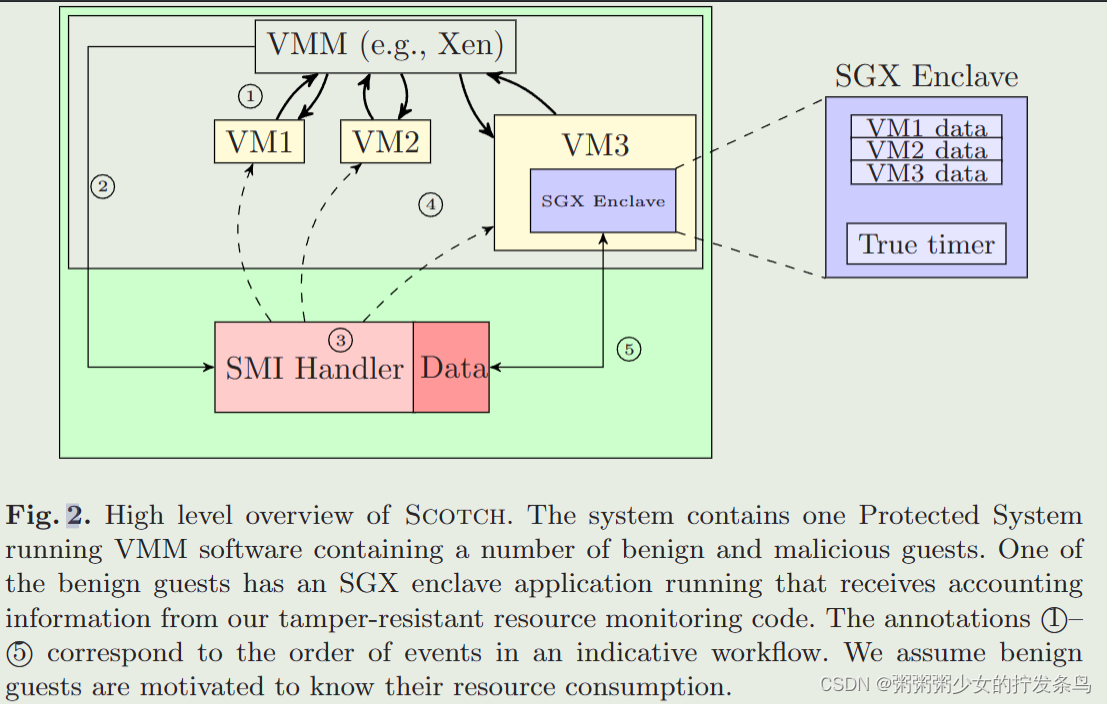
Scotch: Combining SGX and SMM to Monitor Cloud Resource Usage【TEE的应用】
目录 摘要引言贡献 背景SMMXen Credit Scheduler与资源核算SGX 威胁模型Scheduler attacksResource interference attacksVM Escape attacks 架构Resource Accounting WorkflowCost of Accounting 具体的部署和评估见论文相关工作Resource Accounting基于SMM的方法基于SGX的系统…...

腾讯mini项目-【指标监控服务重构】2023-08-19
今日已办 benchmark How can we create a configuration for gobench with -benchmem – IDEs Support (IntelliJ Platform) | JetBrains 本机进行watermill-benchmark 使用 apifox 自动化测试上报固定数量的消息 启动watermill-pub/sub的 benchmark 函数 func BenchmarkPu…...

go实现grpc-快速开始
准备工作 Go, 最新版的 如果不会安装看Getting Started. Protocol buffer compiler, protoc, version 3. 想要安装, 请读Protocol Buffer Compiler Installation. 为 protocol compiler安装Go plugins: 想要安装运行以下命令: $ go install google.golang.org/protobuf/cmd/…...

linux上的init 0-6指令作用以及一些快捷键和系统指令
目录 linux上的init 0-6指令作用 CtrlAltF1-F7作用 Linux常用系统指令 查看linux内核版本 ubuntu和centos查看系统版本信息以及硬件信息 linux上的init 0-6指令作用 在Linux系统中,运行级别(也称为init级别)用来表示系统的不同状态或操作…...

Mixin 混入
Mixin 混入 混入 (mixin) 提供了一种非常灵活的方式,来分发 Vue 组件中的可复用功能。一个混入对象可以包含任意组件选项。当组件使用混入对象时,所有混入对象的选项将被“混合”进入该组件本身的选项。 怎么理解呢,就是每一个组件都会有一…...

pycharm快捷键
CtrlAltL 代码规范化 CtrlHome 回到代码最开始 CtrlEnd 回到代码最后面 shift回车 鼠标任意位置的下一行 altj 一直按可以选中相同的变量 alt鼠标左键 可以选择多个需要修改的变量或值 将光标放在某一行,home到最前面,end到最后…...

【面试刷题】——Linux基础命令
Linux基础命令是在Linux操作系统中执行常见任务的一组命令。以下是一些常用的Linux基础命令,它们用于管理文件系统、执行系统任务、查看文件内容等。 文件和目录操作: ls: 列出目录中的文件和子目录。 pwd: 显示当前工作目录的路径。 cd: 更改当前工作…...

第四步 Vue2 配置ESLint
ESLint 是一个广泛使用的 JavaScript 代码检查工具,可以帮助开发者在编写代码时发现并修复潜在的问题和错误。 在 第一步 创建工程 时虽然已经选择了包含 ESLint 预设配置,但还需要做一些调整,让我们使用起来能够更加的丝滑。 vue.config.j…...

[.NET学习笔记] - Thread.Sleep与Task.Delay在生产中应用的性能测试
场景 有个Service类,自己在内部实现生产者/消费者模式。即多个指令输入该服务后对象后,Service内部有专门的消费线程执行传入的指令。每个指令的执行间隔为1秒。这里有两部分组成, 工作线程的载体。new Thread与Task.Run。执行等待的方法。…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
