Zookeeper 源码分析流程
文章目录
- 前言
- Zookeeper启动
- 加载磁盘数据
- 与客户端的通信交互
- Leader选举准备
- 节点状态处理
- 总结
前言
Zookeeper 作为分布式协调服务为分布式系统提供了一些基础服务,如:命名服务、配置管理、同步等,使得开发者可以更加轻松地处理分布式问题。
在分布式系统中,协调是一项关键任务。例如,如何让一组独立的进程或机器知道它们应该执行哪些任务,如何将它们的状态同步到其他进程或机器上,以及如何处理故障或异常等。这些问题都是 Zookeeper 所解决的问题。
本文将带你深入了解 Zookeeper 的内部实现,从其各个组件和接口开始,分析其工作原理和设计思想。希望你在阅读这个源码分析的过程中,能够深入理解 Zookeeper 的工作原理和设计思想,从而更好地利用它来解决你的分布式问题。
Zookeeper启动
无论看什么代码,我们都应该从程序的入口点入手,这样可以更好地理解整体的结构和运行流程。
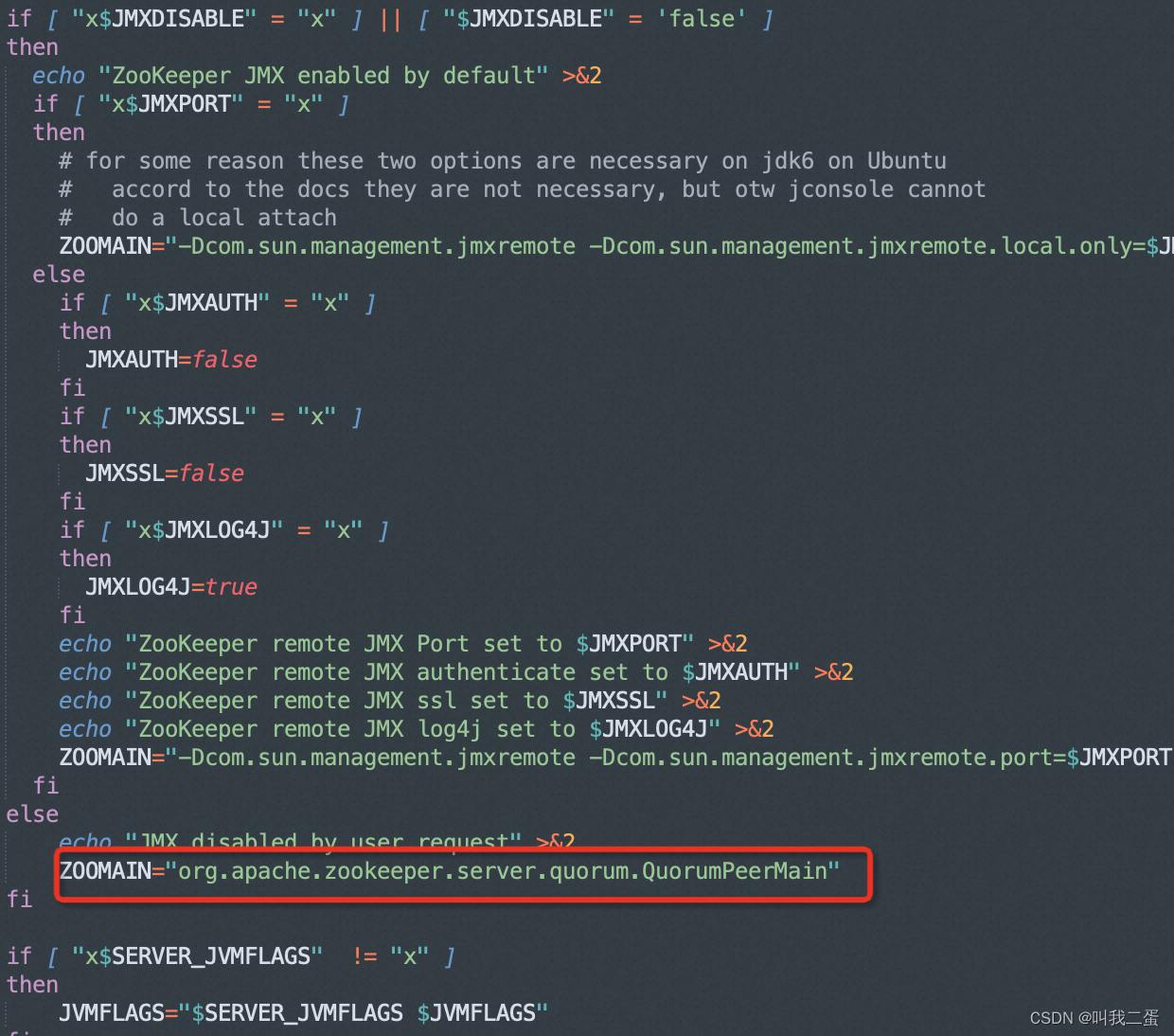
通过 zkServer.sh 脚本可以看到启动类为QuorumPeerMain。
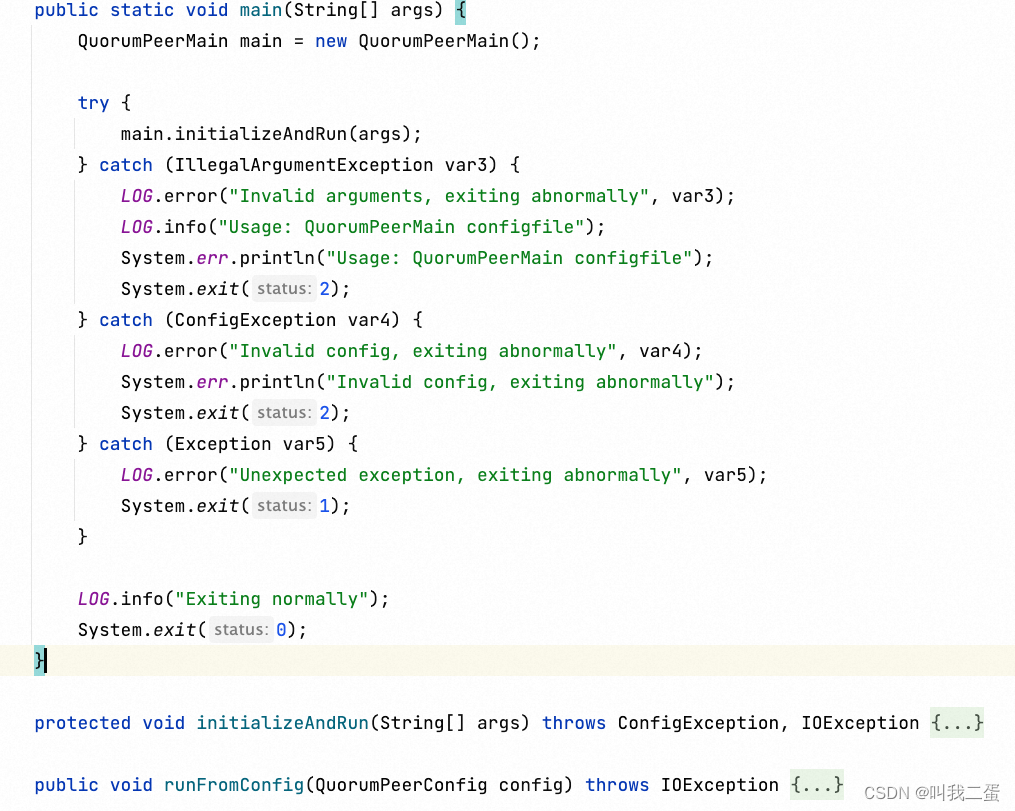
可以看到Zookeeper启动是通过main方法开始的,最终调用了runFromConfig方法设置并启动一个ZooKeeper的集群节点。
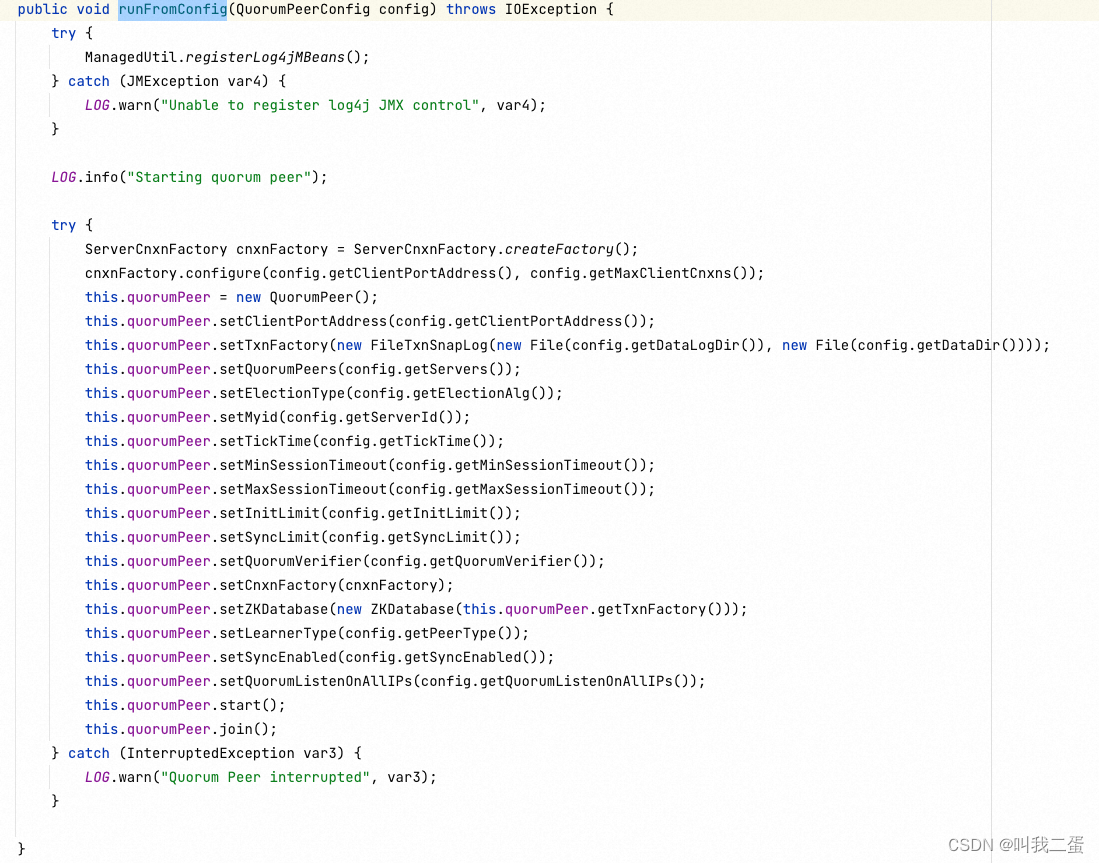
上面的代码设置了QuorumPeer的事务日志和快照目录路径、选举算法选择、指定服务器ID、定义时钟周期和数据保存实例等配置。此外,还创建了服务器和客户端连接的工厂类(NIO/Netty)。最后,调用start方法启动服务。

在start中,主要完成了以下四个任务:
- 将磁盘中的数据加载到内存中,为后续的处理和响应提供必要的数据储备。
- 建立Socket来处理客户端的请求,实现与客户端的通信交互。
- 进行了Leader的选举准备工作,确定选举算法。。
- 进行Leader选举并对节点状态进行监听并相应处理,及时发现和处理节点故障或异常状态,确保整个系统的可靠性和稳定性。
加载磁盘数据
ZooKeeper 操作事内存级别的,为了保障可靠性,会将数据以事务日志形式持久化到文件中,所以在启动时先加载数据到内存。
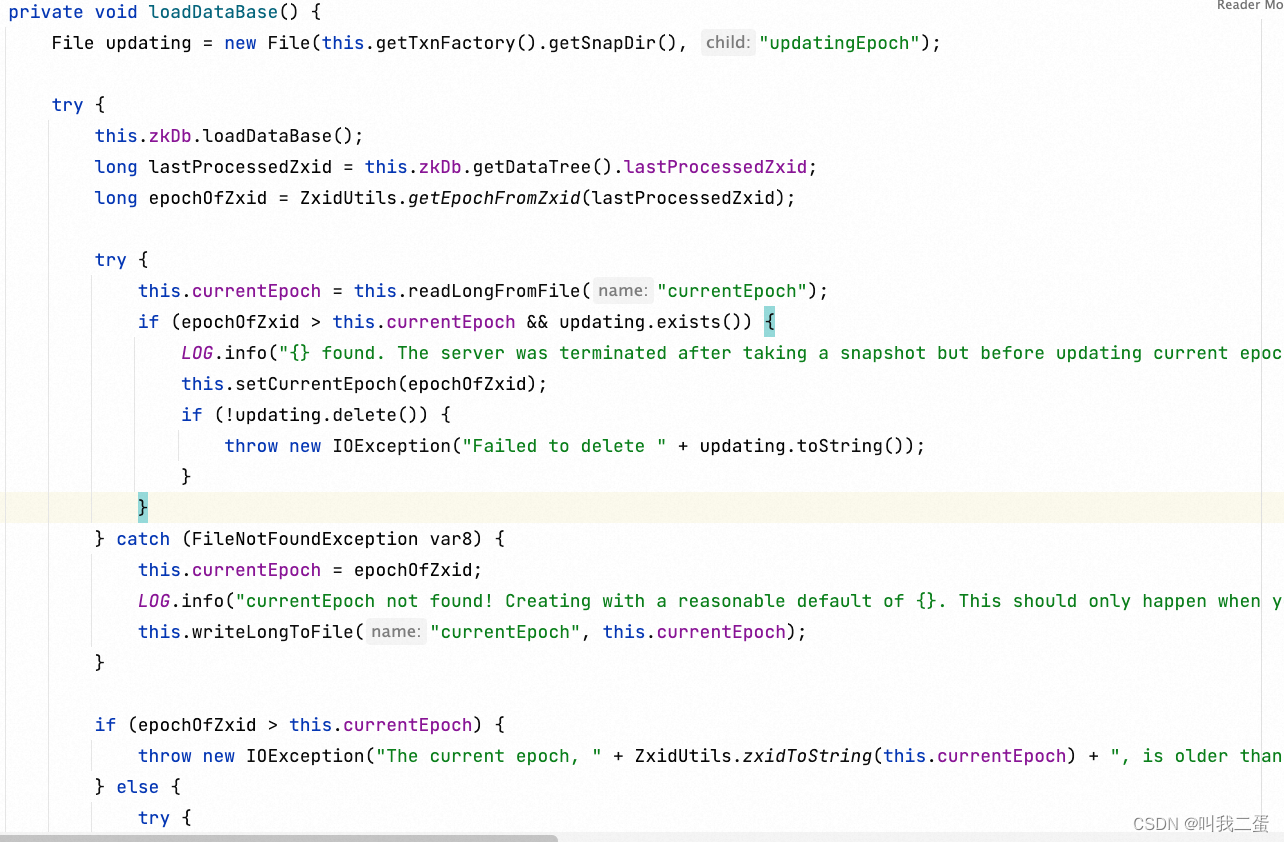
这段代码的主要目的是从磁盘加载Zookeeper数据库到内存,并检查并处理相关的epoch信息。getDataTree().lastProcessedZxid 这行代码获取在ZooKeeper服务器上已处理的最新的事务的zxid,ZxidUtils.getEpochFromZxid(lastProcessedZxid)这行代码从zxid中获取epoch,readLongFromFile(CURRENT_EPOCH_FILENAME): 这行代码从文件中读取当前的epoch信息。如果zxid所属的epoch小于当前的epoch,会抛出IOException异常。
与客户端的通信交互
cnxnFactory 是建立了Socket 服务端,用来接收客户端的请求并处理,下图中的代码是NIOServerCnxnFactory,还有一个NettyServerCnxnFactory。选用NIO还是Netty可以在配置文件中设置。对NIO和Netty不熟悉的可以看下网络编程专栏
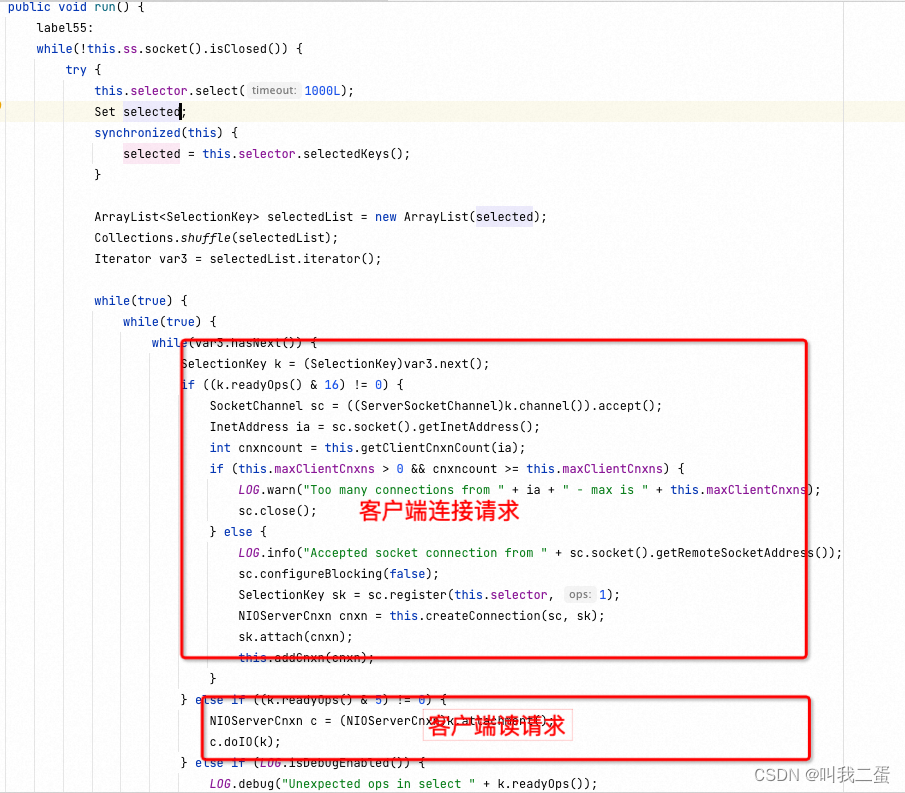
最核心的就是对客户端请求的处理,有如下几个处理器:

CommitProcessor是事务提交处理器,它会等待集群内针对Proposal的投票直到该Proposal可以被提交。SyncRequestProcessor负责把事务请求(写request)持久化到本地磁盘。AckRequestProcessor是Leader特有的处理器,其主要职责是在SyncRequestProcessor处理器完成事务日志记录后,向Proposal的投票收集器发送ACK反馈,以通知投票收集器当前服务器已经完成了对该Proposal的事务日志记录。FollowerRequestProcessor这个处理器可能会负责处理来自客户端的读请求和写请求,并将其转发给其他处理器进行处理,比如写请求转发给Leader节点。SendAckRequestProcessor负责向领导者(Leader)节点发送确认收到的消息(ACK),通知领导者节点该请求已经得到处理。
Leader选举准备
startLeaderElection 中主要调用了createElectionAlgorithm 创建了集群间网络连接的管理器 QuorumCnxManager,并选择了一个选举算法,这个通过配置文件配置,默认为FastLeaderElection。
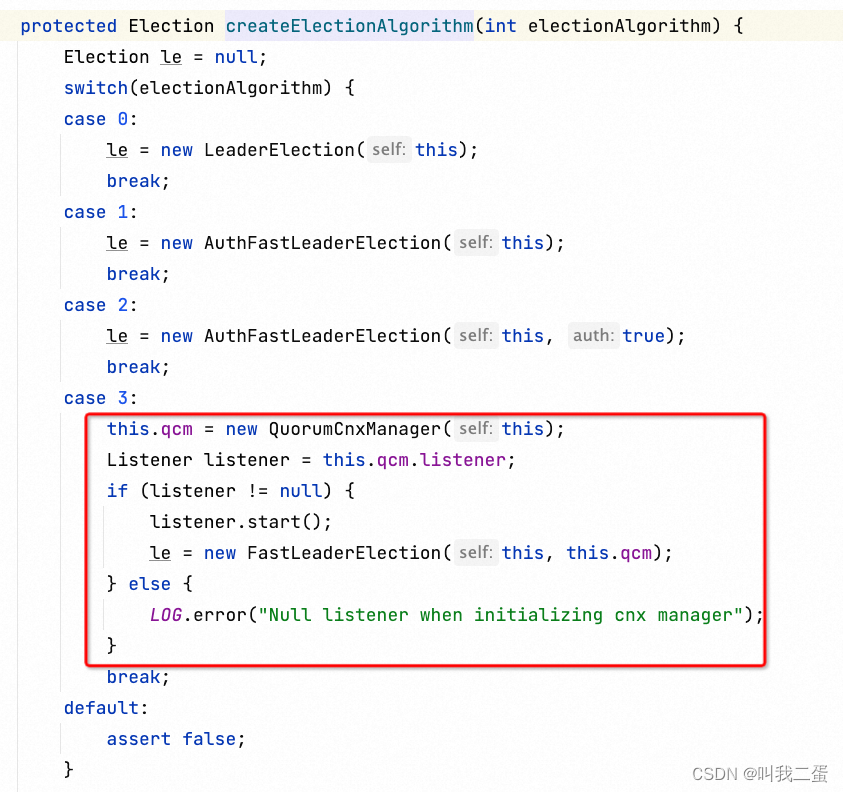
节点状态处理
super.start()执行 QuorumPeer.java 类中的 run()方法,主要是对节点状态的监听及处理。
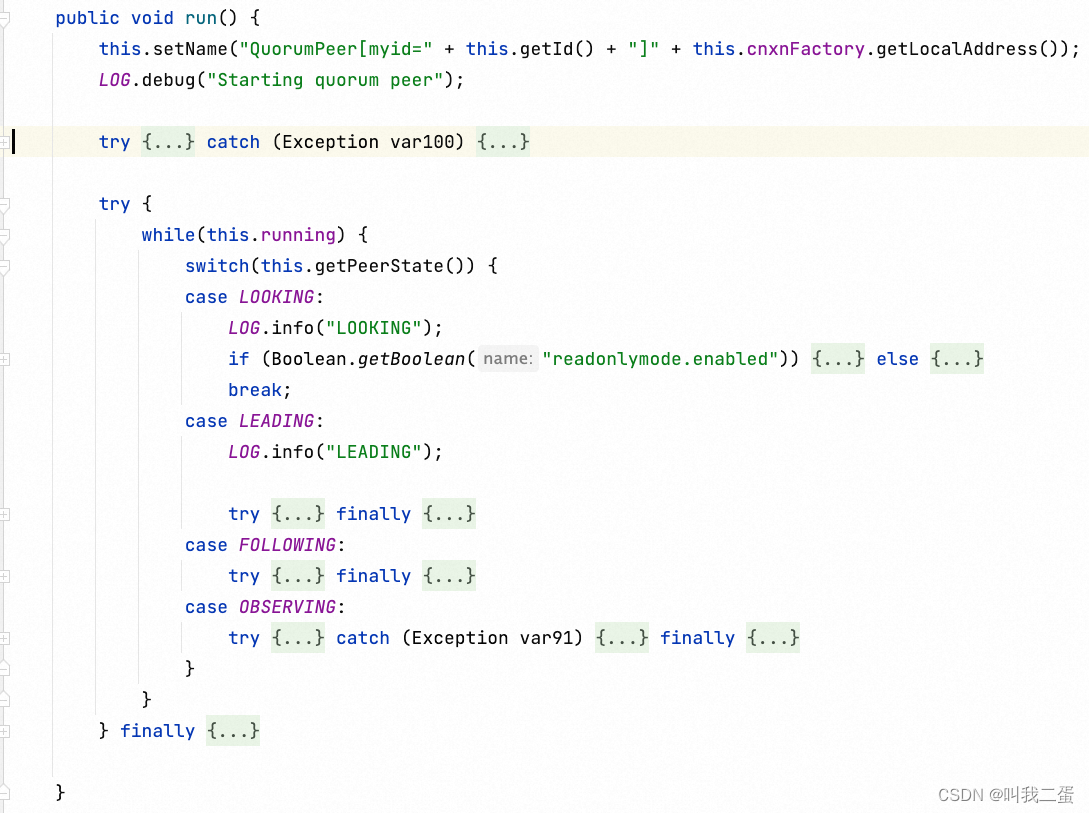
当 Zookeeper 启动后,首先都是 Looking 状态,通过选举,让其中一台服务器成为 Leader,其他的服务器成为 Follower。如果代码比较难理解可以看一下ZAB协议。
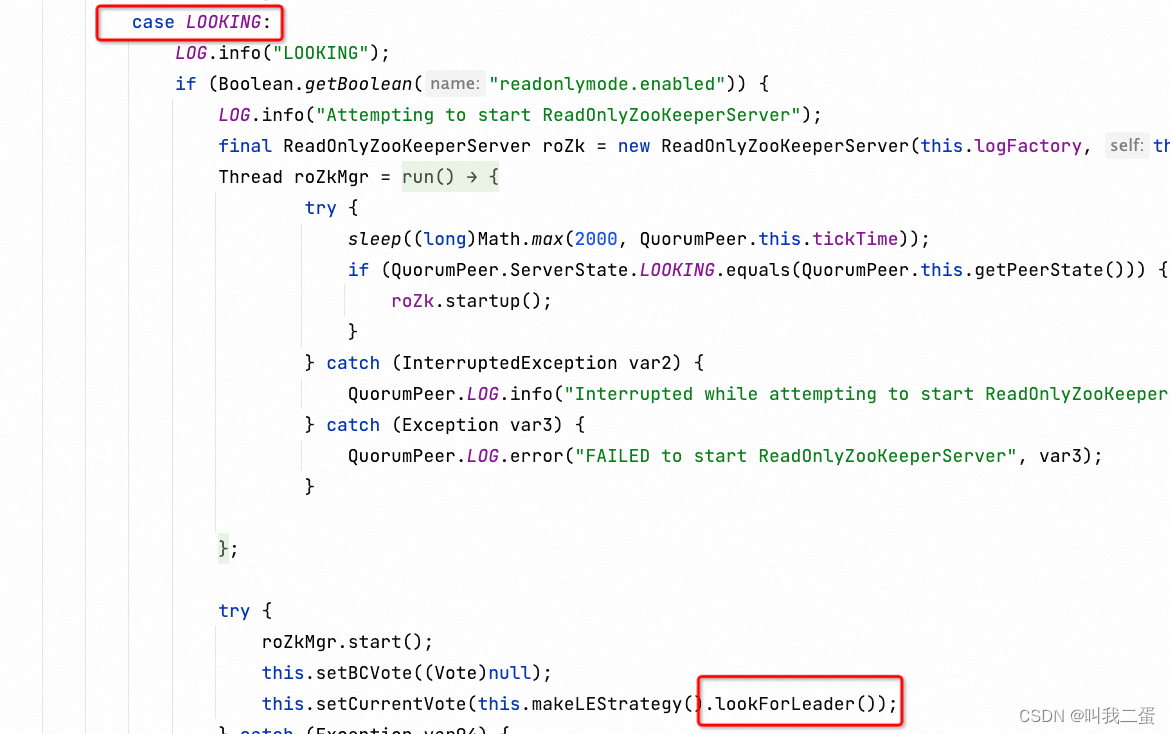
总结
通过深入解析源代码,我注意到其简洁性以及对功能实现的巧妙设计。尽管代码所处理的功能相当复杂,但组织结构和代码风格的简洁性使得阅读和理解变得相当容易。特别注意到网络编程的大量应用,对连接安全和优化的细致处理。还有其ZAB协议如何巧妙地解决了分布式一致性问题,这些细腻的设计理念无疑为分布式系统的开发提供了宝贵的借鉴,期待能在未来的工作中将这些思想融入到的代码中。
相关文章:

Zookeeper 源码分析流程
文章目录 前言Zookeeper启动加载磁盘数据与客户端的通信交互Leader选举准备节点状态处理总结 前言 Zookeeper 作为分布式协调服务为分布式系统提供了一些基础服务,如:命名服务、配置管理、同步等,使得开发者可以更加轻松地处理分布式问题。 …...

计数排序与基数排序
计数排序与基数排序 计数排序 计数排序:使用一个数组记录序列中每一个数字出现的次数,将该数组的下标作为实际数据,元素的值作为数据出现的次数。例如对于序列[3,0,1,1,3,3,0,2],统计的结果为: 0出现的次数…...

Mysql—表操作
目录 1、linux中数据库表名区分大小写,windows不区分2、创建数据库表3、外键4、查看数据表结构5、修改表5.1、修改表名5.2、添加字段5.3、指定位置添加字段5.4、修改字段名称5.5、修改字段类型5.6、修改字段位置5.7、删除字段5.8、修改表存储引擎5.9、删除外键 1、l…...

SpringCloud——微服务
微服务技术栈 在之前的开发过程中,我们将所有的服务都部署在一台服务器中,当我们的服务开始越来越多,业务越来越复杂,当一台服务器不能承担我们的业务的时候,就需要将不同的业务分开部署在不同的服务器上,…...
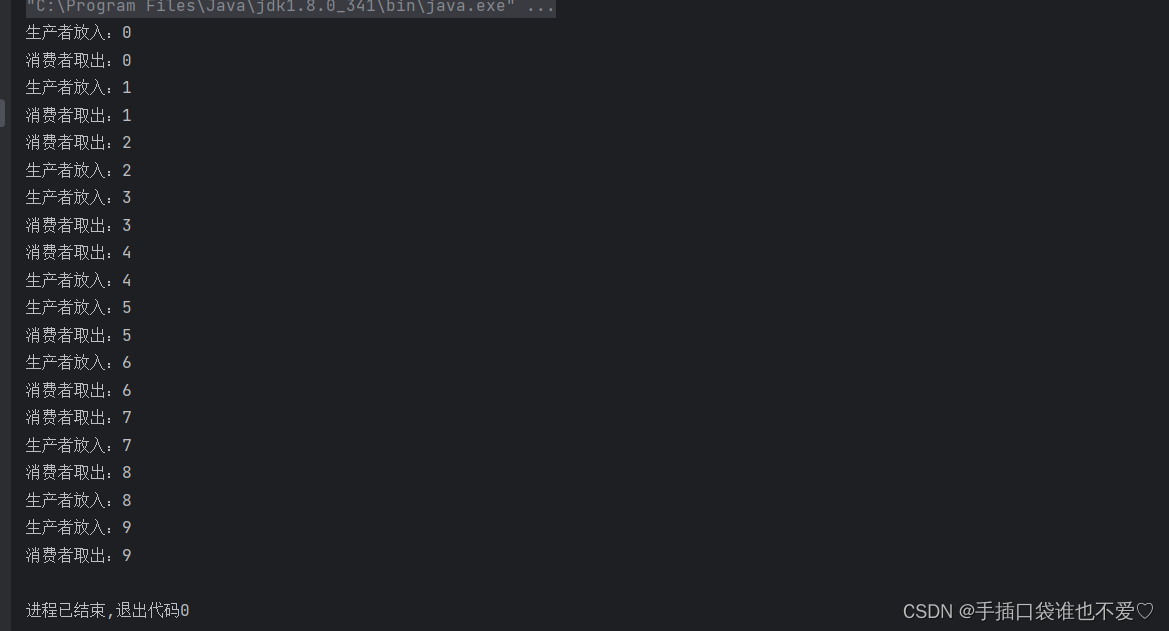
深入理解Java单例模式和优化多线程任务处理
目录 饿汉模式懒汉模式单线程版多线程版双重检查锁定 阻塞队列 单例模式能保证某个类在程序中只存在唯一一份实例, 而不会创建出多个实例,并提供一个全局访问点。 饿汉模式 类加载的同时,创建实例。 class Singleton {private static final Singlet…...

已解决 Kotlin Error: Type mismatch: inferred type is String but Int was expected
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页: 🐅🐾猫头虎的博客🎐《面试题大全专栏》 🦕 文章图文并茂🦖…...
Web应用系统的小安全漏洞及相应的攻击方式
写作目的 本文讲述一个简单的利用WebAPI来进行一次基本没有破坏力的“黑客”行为。 主要目的如下: 了解什么叫安全漏洞 知道什么是api 了解一些获取api的工具 通过对API的认识了解白盒接口测试基本概念和技术 免责声明: 本文主要是以学习交流为目的&a…...

git工具下载和安装
(1)从git官网下载安装包 然后安装 https://git-scm.com/downloads (2)git 学习参考官方的资料 https://git-scm.com/book/en/v2...
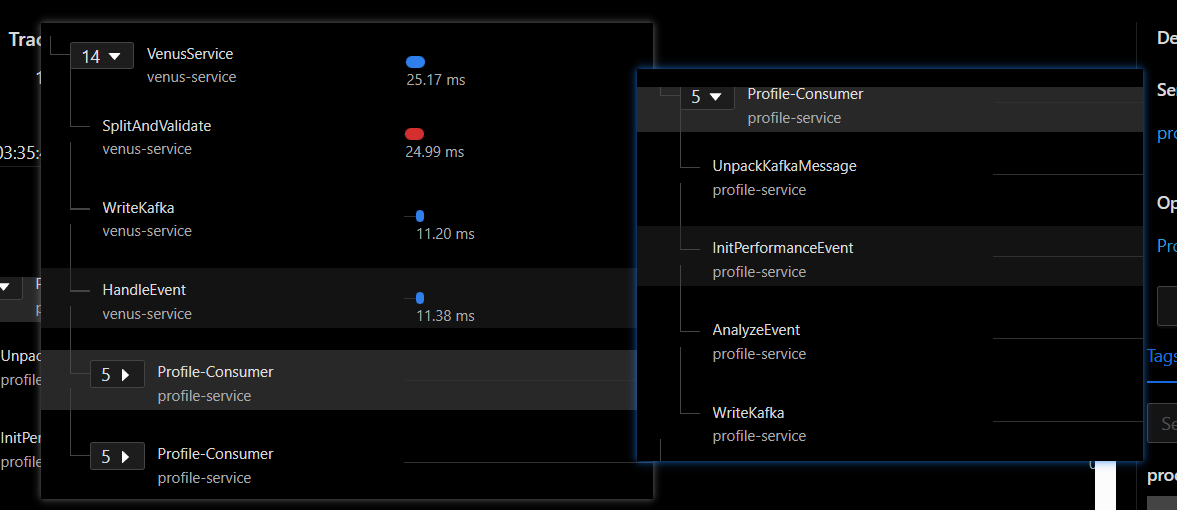
腾讯mini项目-【指标监控服务重构】2023-08-04
今日已办 关于 span-references 的调研 https://github.com/DataDog/dd-trace-js/issues/1761 https://github.com/open-telemetry/opentelemetry-specification/blob/874a451e7f6ac7fc54423ee3f03e5394197be35b/specification/compatibility/opentracing.md#span-references h…...
怎么推广自己抖店的商品?最适合0经验新手操作的办法,来看看
我是王路飞。 抖店开通后,想要把自己店铺的商品卖出去,就需要进行推广了。 但是怎么推广呢? 要么利用抖音的搜索和推荐流量,获取曝光,实现点击和转化。 不过这种玩法有个弊端,就是需要你有一定的电商经…...
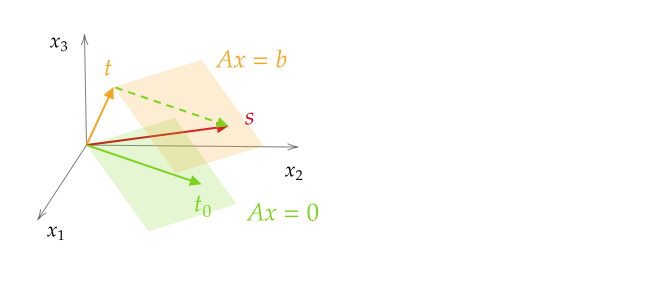
线性代数的本质(三)——线性方程组
文章目录 线性方程组高斯消元法初等行变换线性方程组的解向量方程齐次线性方程组的解非齐次线性方程组的解 线性方程组 高斯消元法 客观世界最简单的数量关系是均匀变化的关系。在均匀变化问题中,列出的方程组是一次方程组,我们称之为线性方程组(Linea…...

轻量级性能测试工具 wrk 如何使用?
项目设计之初或者是项目快要结束的时候,大佬就会问我们,这个服务性能测试的结果是什么,QPS 可以达到多少,RPS 又能达到多少?接口性能可以满足未来生产环境的实际情况吗?有没有自己测试过自己接口的吞吐量&a…...

WebGL 视图矩阵、模型视图矩阵
目录 立方体由三角形构成 视点和视线 视点、观察目标点和上方向 视点: 观察目标点: 上方向: 在WebGL中,观察者的默认状态应该是这样的: 视图矩阵程序(LookAtTriangles.js) 实际上&…...
 方法)
Python 3 – 文件 readline() 方法
Python 3 – 文件 readline() 方法|极客笔记 # 打开文件 file open("example.txt", "r")# 读取文件中的一行数据 line file.readline() while line:# 移除行尾的换行符print(line.strip())# 读取文件中的下一行数据line file.readline()# 关闭文件 file…...
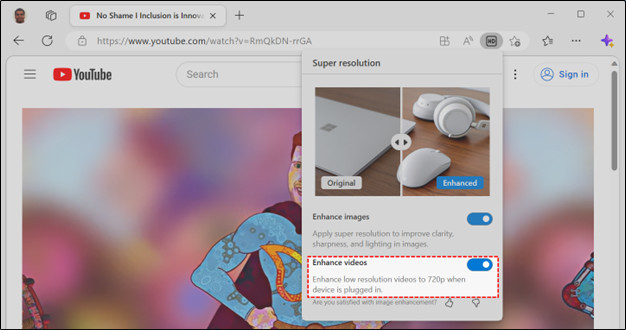
如何在微软Edge浏览器上一键观看高清视频?
编者按:视频是当下最流行的媒体形式之一。但由于视频压缩、网络不稳定等原因,我们常常可以看到互联网上的很多视频其画面质量并不理想,尤其是在浏览器端,这极大地影响了观看体验。不过,近期微软 Edge 浏览器推出了一项…...

Telegram BoT的主流项目盘点
目录 DeFi 类 数据分析类 空投埋伏交易 其他 Telegram Bot赛道的发展趋势预测 Telegram BoT赛道发展较快,具体来看可以分为DeFi 类、数据分析类、空投埋伏交易类以及其他。 DeFi 类 Unibot(交易)、Banana Gun、WagieBot(交…...

PTA 甲级 1044 Shopping in Mars
题目链接 思路:前缀和滑动窗口 #include<bits/stdc.h> #define MAXN 100010 using namespace std; int a[MAXN];int main(){int n,m;cin>>n>>m;//n数量 m金额for(int i1;i<n;i){int t;cin>>t;a[i]a[i-1]t;//前缀和}vector<pair<in…...

Linux学习之MyCat实现分库分表
环境准备 先准备一套MySQL主从服务器,可参考MySQL主从配置配置MyCat服务 资源下载 网盘链接: https://pan.baidu.com/s/1cLTMH_e1-6loc_gF9ZNHTg?pwda63n 提取码: a63n MyCat配置 # 1)安装mycat软件 //安装jdk [rootmycat58 upload]# yum -y insta…...

DirectX12(d3d12)初始化
一、前置要求 Windows 10及以上(安装有DirectX12)VisualStudio 2022 二、DirectX12入门 1.引用头文件 #include<Windows.h> #include<d3d12.h> #include<dxgi1_4.h>2.注册窗口类并初始化窗口 这里我们调用Windows API 通过应用程序的句柄来注册一个唯一…...

算法通关村-----回溯模板如何解决排列组合问题
组合总和 问题描述 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
