线性代数的本质——几何角度理解
B站网课来自 3Blue1Brown的翻译版,看完醍醐灌顶,强烈推荐:
线性代数的本质
本课程从几何的角度翻译了线代中各种核心的概念及性质,对做题和练习效果有实质性的提高,下面博主来总结一下自己的理解
1.向量的本质
在物理中的理解是一个有起点和终点的方向矢量,而在计算机科学中的理解——更像是某种类似于列表的结构体(只不过这是一种以数字为元素的列表)。
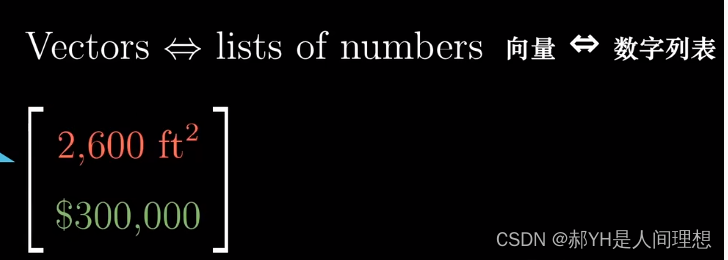
对应在数学的领域,可以理解为一种坐标——分别用列表中的项来对应起点与终点(二维向量)。
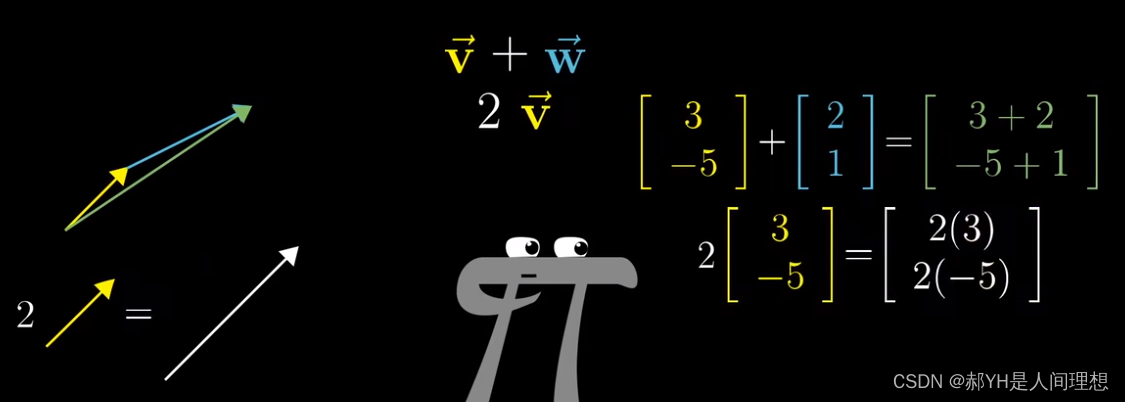
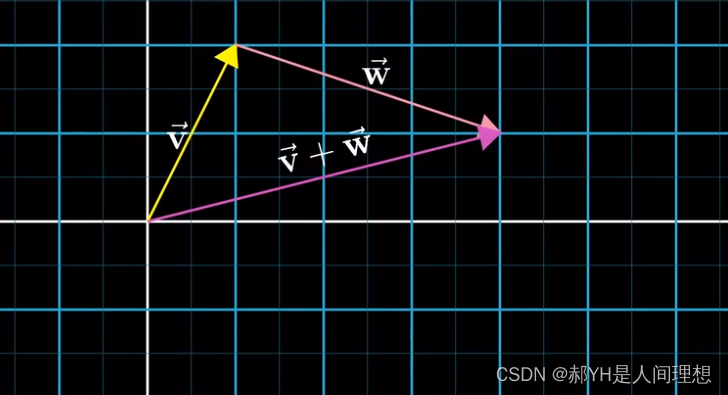
而向量加法的本质,即为对应维度上的线性相消。 而另一种理解为,向量是空间中的某种运动,在不同维度上的线性抵消,如下图——这一性质也可以扩展到n维。
2.向量的坐标
首先理解单位向量的概念——i(1,0),j(0,1),由i与j的线性相加可以得到空间中的任一向量~
而向量【-3,2】,可以将两个元素理解为2个标量——即对向量的拉伸与压缩。
而基向量,也就是单位向量,即为所谓拉伸与压缩的对象!
两个数型向量的相加,被称为这2个向量的线性组合~
对于线性的一种理解:只允许1个标量变化,其余n-1个维度的坐标固定,所产生的向量集即为一条直线!
3.张成空间
定义:所有可以表示为给定向量线性组合的向量的集合。
- 对于二维,表示所有二维空间中向量的集合,亦或终点相同的向量的集合
- 对于三维,表示一个平面或者一个空间
4.线性相关与线性无关
- 所谓线性相关,即向量组中至少有一个是多余的,即没有对张成空间的形成做出贡献——换句话说,有至少一个向量可由其他向量线性相加获得(线性组合)
- 而所谓线性无关,即每一个向量的存在都会使得张成空间的维度增加
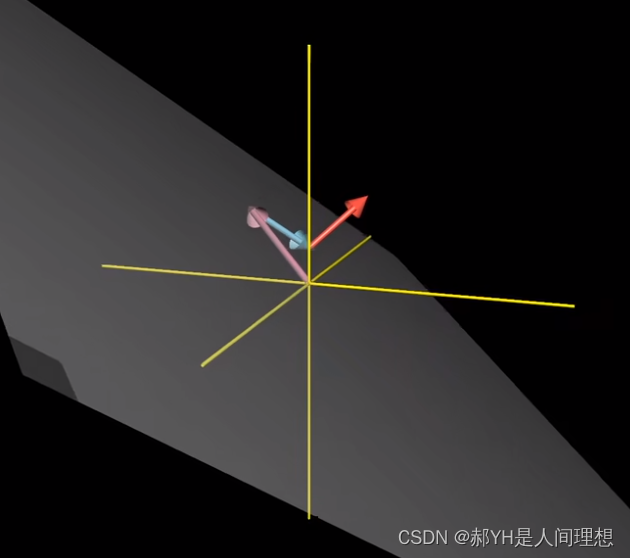
5.矩阵的本质——线性变换
所谓变化,其实就是函数的一种花哨说法~
本质上,向量a是由i和j的一个线性组合,而空间发生变化后a1则变为了同样发生变化的i1与j1与原来保持一致的线性组合!

所以,如果将变化后的i1与j1按照列向量合集表示,如下图,即形成了所谓的矩阵!
也就是说,在二维空间的线性变换,仅由4个数就可以决定!
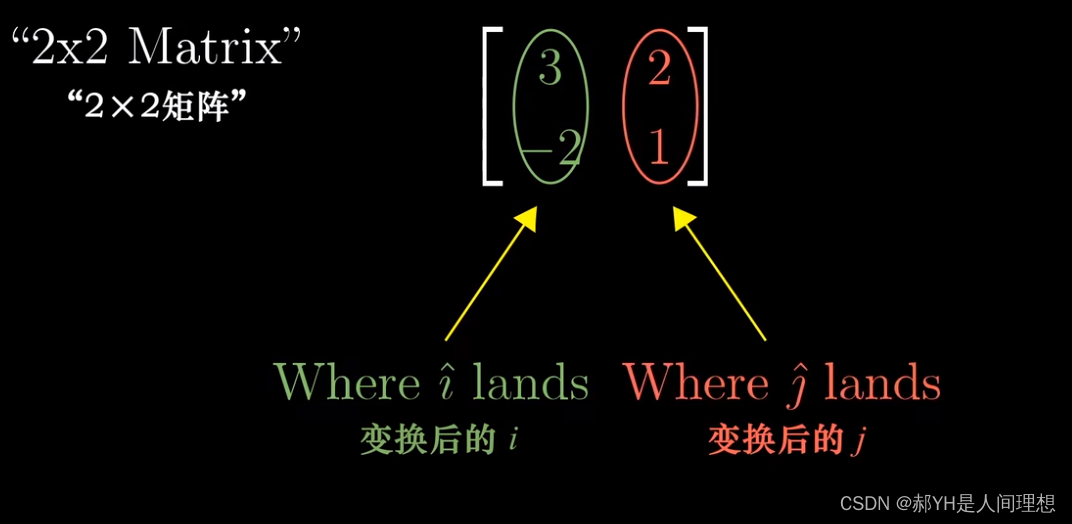 此刻若给出一个矩阵和一个已知变量 ,即可得出:对该向量进行目标矩阵的变换后可以得出的新向量!
此刻若给出一个矩阵和一个已知变量 ,即可得出:对该向量进行目标矩阵的变换后可以得出的新向量!
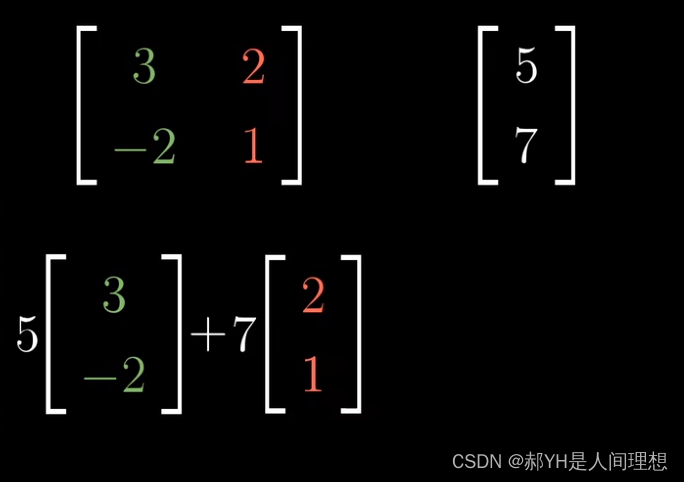
关于上面的一个理解,不要晕:所谓的5/7,本质上的意味是:a=5i+7j,也就是说,所谓的目标向量,本质也是对i和j的一种变化!!!而为什么有的变化就是向量,而有的变化就是矩阵呢?那是因为,所谓的5/7,他对应的均为当前方向上的变化——即翻倍延长,而矩阵中,第一行的变化,均为在i方向上的变化,而第二行则全部对应j方向的变化——也就是说,矩阵变化后的i1和j1,实际上是在两个方向上同时变化!!!因此不难理解矩阵乘法的底层逻辑:这里第一行乘以第一列的意义,实际上是原来对应的5i,在i变成i1后所需要对应的变化——即i方向变3,j方向变2!第二行也是同理~此刻即使扩展到n维,这一原理仍成立!
再进行一个更炸裂的理解:所谓m行n列的矩阵,m即为当前基向量的个数——即坐标系的维度,而所谓的mn列,即为对原始的基向量,需要进行几维的线性变换!
因此,我们可以说:矩阵的本质就是一种线性变换!(也就是作用于向量的函数)
6.矩阵的乘法
如果将矩阵理解为一种线性变换,那么矩阵的相乘本质即为连续的线性变换~

注意一个细节——同函数一致,需要向右往左看!
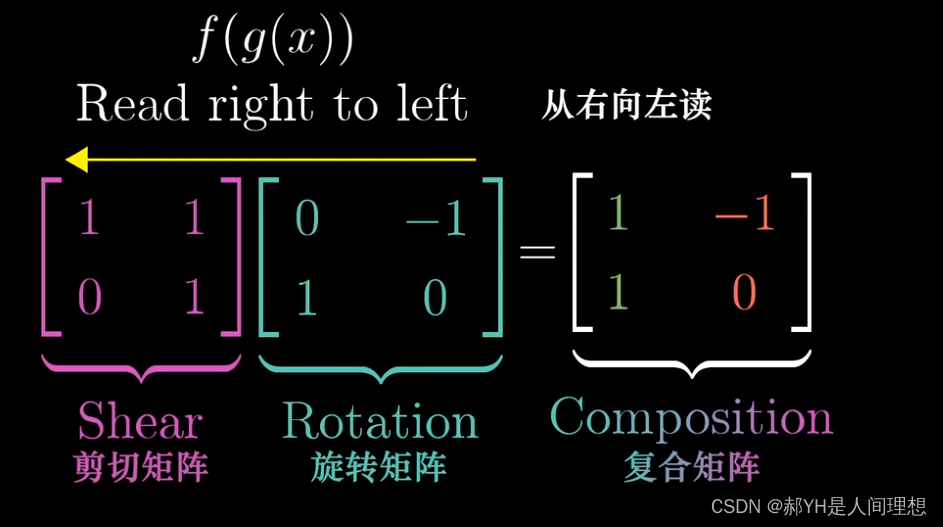
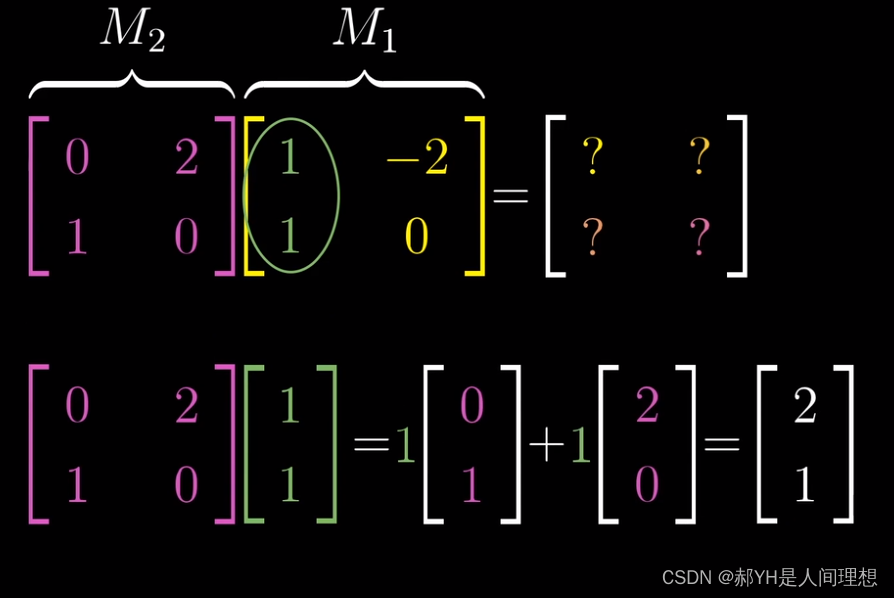
对于相乘后得到的矩阵:第一列即为第一个矩阵进行变换变为i1后,第二个矩阵使他变换为了i2;j2的诞生亦是如此~
至于乘法的规则,再描述一遍:如上的1/1,即为对i的变化,现在需要将i1变化为i2,则需要再对i1进行i和j两个维度上的一次变化! 所以i1的i方向1在i上变0,j上变1;j1的i方向上2而j方向上变0!
非常抽象,需要反复琢磨!
7.三维空间中的线性变换
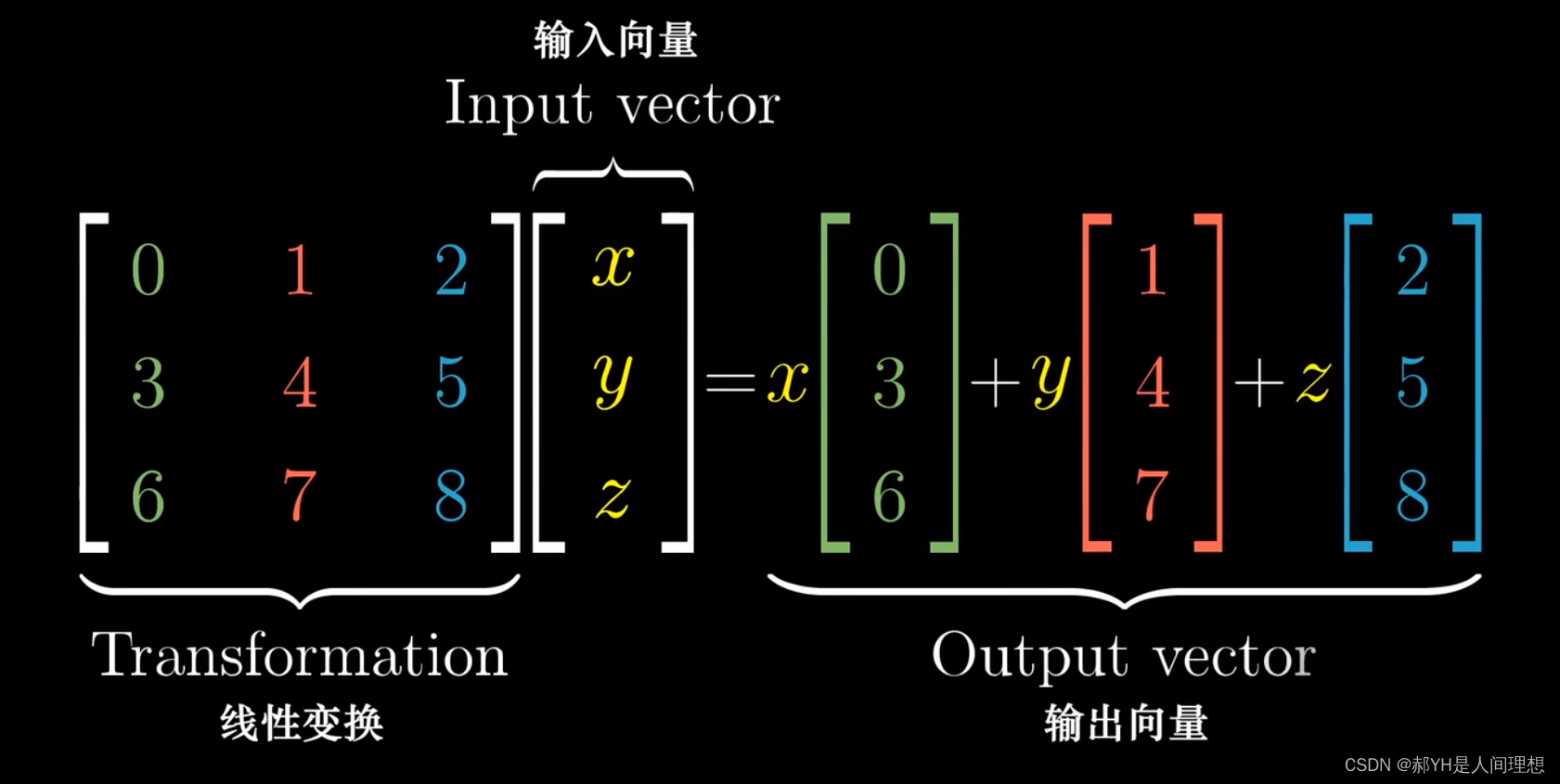
同二维平面一致,此处仅需要9个数,即可完成三维空间下的线性变换,将这9个数组为三维向量。
此处对3维方阵与向量的乘积做出如下两种理解:
- 首先,按列看,1~3列可以分别对应为基向量i、j、k的线性变换,而按行看,则代表i、j、k向量在当前所对应的维度上各自的变化量。
- 另一种解释,如上图,xyz后面的向量,实际意义是经过线性变换后坐标系里的基向量,而此刻把xyz可以理解为一种给定的标量,并作用于当前变换后的基向量
8.行列式
单位正方形:在二维平面内,以i和j两个基向量为边所圈成的正方形
行列式的本质,即为线性变换对原面积改变的比例——行列式的值即为对面积的缩放比例数值
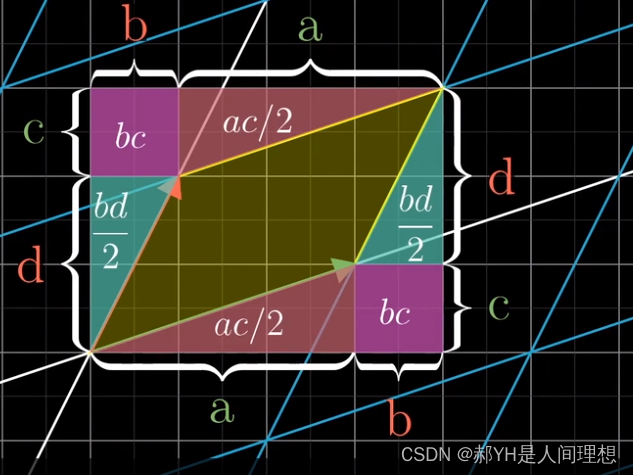
- 在二维平面里,如果行列式的值为负,本质是在将矩阵翻转~
- 在三维空间里,行雷士的值即为对应体积的缩放比例~
在三维的情况下,当行列式为0时,即当前的体积被压缩为0,几何角度的理解为:存在共线向量、共面甚至重合的一个点!——这便是所谓线性相关的几何意义。
这也从某种角度解释了——为什么对应的行列式为0的向量组必然线性相关,实质上还是那个理解,存在未对维度变化做出贡献的向量
(可以说,空间压缩的本质是行列式为0)
9.线性方程组
首先要注意——线性方程组存在的意义和向量的乘法非常的类似~
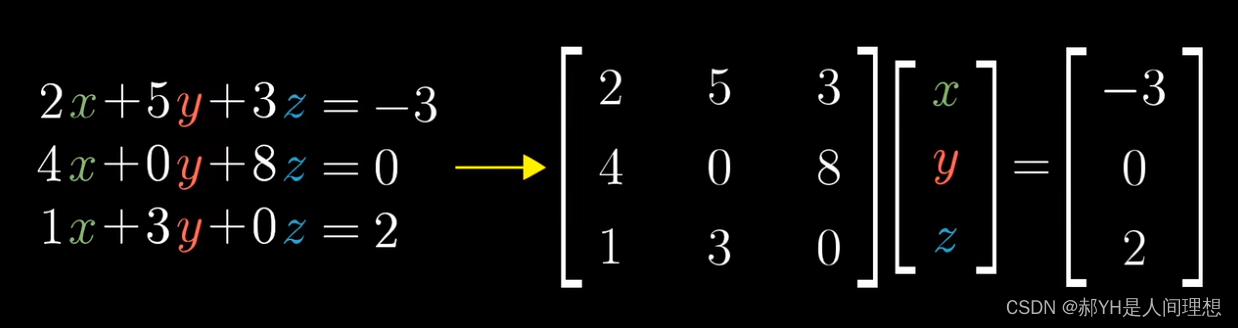
如上是一种非常具有技巧性的理解:方程组可以表示为矩阵与向量的积
其中系数矩阵A本质上就是对于向量的某种函数;而这里的向量是一个未知数,由x/y/z三个未知的数值表示。
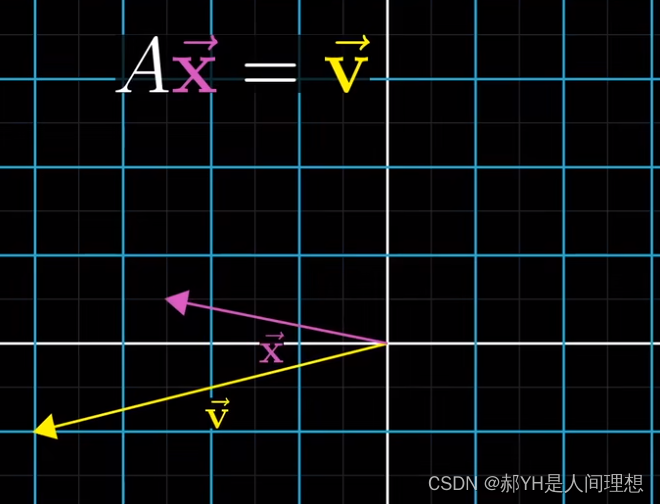
上述Ax=v的理解可以有两种:
- 矩阵代表一种线性变换,在一元函数中可以理解为k、b这样的常数,而xyz组成的向量本质上就是一元函数中的自变量
- 同理,依旧可以理解为,xyz是对当前经过矩阵A变换后的新的基向量的数值,则这一方程本质上变为了求解标量xyz的过程
10.逆矩阵
顾名思义,几何意义即为逆向的线性变换。
存在的意义为,A-1和A可以相互抵消,形成一个本质上什么都做的变换,这样的变换又被称为恒等变换
单位矩阵E的集合意义在这里就解释得同了:对角线为1的性质,带来了仅对当前向量的基向量所对应维度的变换,且倍数为1。
11.秩
本质为线性变换后的空间维数(国内的课本定义为:非0子式的最高阶数......)
秩为1表示变换后的直线落在一条一维的线上,秩为2表示为二维空间
列空间:所有可能得输出向量所构成的集合——所以秩也可以定义为列空间的维数
满秩:秩数与列数相等
12.非方阵的矩阵

如上图,结合一个具体的例子产生矩阵的数值意义:2列代表着,输入空间有两个基向量,即该向量的张成空间可以理解为是二维的;而3行,又意味着每一个基向量又有3个坐标组成。而这样一个三行两列的句子,意味着空间中的一个平面。
总的来说,矩阵的行数即为当前向量坐标的个数,而列数则是基向量的个数~

因此这里提出一个比较炸裂的理解:为什么不是方阵的矩阵均没有行列式呢?这是因为,方阵与向量的积不会改变向量的维度,而矩阵本身又是一个线性变换,所以可以理解为乘以对应的行列式——即某个倍数;而矩阵乘以一个向量,会改变向量的维度!因此在不同的维度下讨论倍数,便不再具有意义。这里打个比方,有一桶水,所谓的伸缩本质上就是给水桶里添加/减少容量的过程,而如果水洒了一地,维度改变,即不再具有倍数的讨论。
13.特征值与特征向量
特征值:衡量特征向量在变换中拉伸或压缩的比例的因子~
特征向量:线性变换中不离开自己张成空间的特殊向量~
(一部分暂不展开更细的讲解,之后有机会更新)
相关文章:

线性代数的本质——几何角度理解
B站网课来自 3Blue1Brown的翻译版,看完醍醐灌顶,强烈推荐: 线性代数的本质 本课程从几何的角度翻译了线代中各种核心的概念及性质,对做题和练习效果有实质性的提高,下面博主来总结一下自己的理解 1.向量的本质 在物…...

SSH key 运作方式
1、本地创建SSH key pairs 2、把public key上传到网站服务器(如GitHub 3、当使用ssh方式连接时 本地SSH client向远端请求ssh连接远端发来random data要求加密本地ssh client用private key加密,把加密的data发送过去(不发送private key远端接…...

【基于MBD开发模式的matlab持续集成(一)】
基于MBD开发模式的matlab持续集成 引言 或许是感受到行业内卷的愈加激烈,在传统制造和高新技术相结合的新能源领域对软件工程开发的要求也愈加提高,尤其在互联网已经大行 其道的敏捷开发,便顺其自然的被新能源的老板们所看重。 概述 本文…...
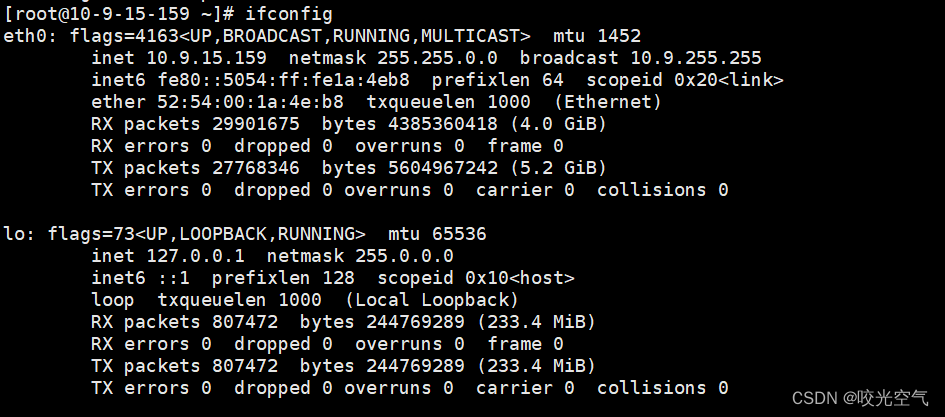
Linux学习记录——이십팔 网络基础(1)
文章目录 1、了解2、网络协议栈3、TCP/IP模型4、网络传输1、同一局域网(子网)2、局域网通信原理3、跨一个路由器的两个子网4、其它 详细的网络发展历史就不写了 1、了解 为什么会出现网络?一开始多个计算机之间想要共享文件,就得…...

CSS动效合集之实现气泡发散动画
前言 👏CSS动效合集之实现气泡发散动画,速速来Get吧~ 🥇文末分享源代码。记得点赞关注收藏! 1.实现效果 2.实现步骤 定义一个数组bubbles,用来存储气泡列表的基本新,w表示宽高,x表示绝对定位…...
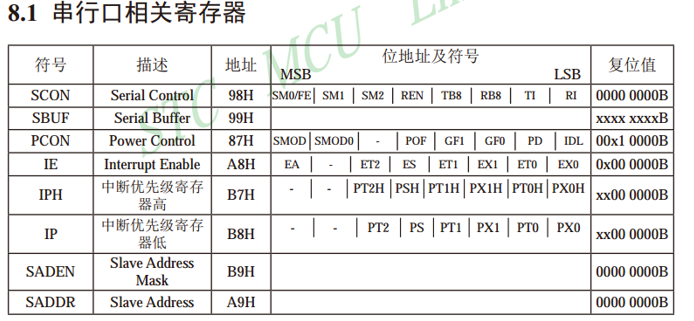
六、串口通信
六、串口通信 串口接口介绍使用串口向电脑发送数据电脑发送数据控制LED灯 串口接口介绍 SBUF是串口数据缓存器,物理上是两个独立的寄存器,但占用相同的地址。写操作时,写入的是发送寄存器;读操作时,读出的是接收寄存器…...

如何将 JavaScript Excel XLSX 查看器添加到Web应用程序
在 JavaScript 中创建 Excel 查看器可能是一项艰巨的任务,但使用 SpreadJS JavaScript 电子表格,创建过程要简单得多。在本教程博客中,我们将向您展示如何使用 SpreadJS 的强大功能来创建一个查看器,该查看器允许您在 Web 浏览器中…...

网安周报|CISA发布增强开源安全性的计划
1、CISA发布增强开源安全性的计划 美国一家领先的安全机构发布了一项期待已久的计划,详细说明了它将如何增强联邦政府和整个生态系统的开源安全性。美国网络安全和基础设施安全局(CISA)开源软件安全路线图在安全开源峰会上发布。据估计&#…...
使用 Docker 安装 Elasticsearch (本地环境 M1 Mac)
Elasticsearchkibana下载安装 docker pull elasticsearch:7.16.2docker run --name es -d -e ES_JAVA_OPTS“-Xms512m -Xmx512m” -e “discovery.typesingle-node” -p 9200:9200 -p 9300:9300 elasticsearch:7.16.2docker pull kibana:7.16.2docker run --name kibana -e EL…...

Visual Studio中MD与MT的区别及运行库类型选择
MT与MD的区别 /MT:是multithread-static version,是多线程静态版本的意思,项目会使用运行时库的多线程静态版本,编译器会将LIBCMT.lib放入.obj文件中,以便链接器使用LIBCMT.lib解析外部符号;/MTdÿ…...

Vue3函数式编程
文章目录 前言一、三种编程风格1.template2.jsx/tsx3.函数式编写风格 二、函数式编程1.使用场景2.参数3.例子3.render渲染函数 总结 前言 本文主要记录vue3中的函数式编程以及其他编程风格的简介 一、三种编程风格 1.template Vue 使用一种基于 HTML 的模板语法,…...
【逗老师的无线电】艾德克斯TTL串口转网口
最近手搓了一个可以用于艾德克斯ITECH电源或者电子负载的TTL串口转网口的模块,用上之后,上位机软件就可以配置以太网IP连接设备啦。就像这样。 一、ITECH TTL接口定义 二、整体逻辑 嗯,就这么简单。IT9000控制软件的Ethernet功能就是直接S…...
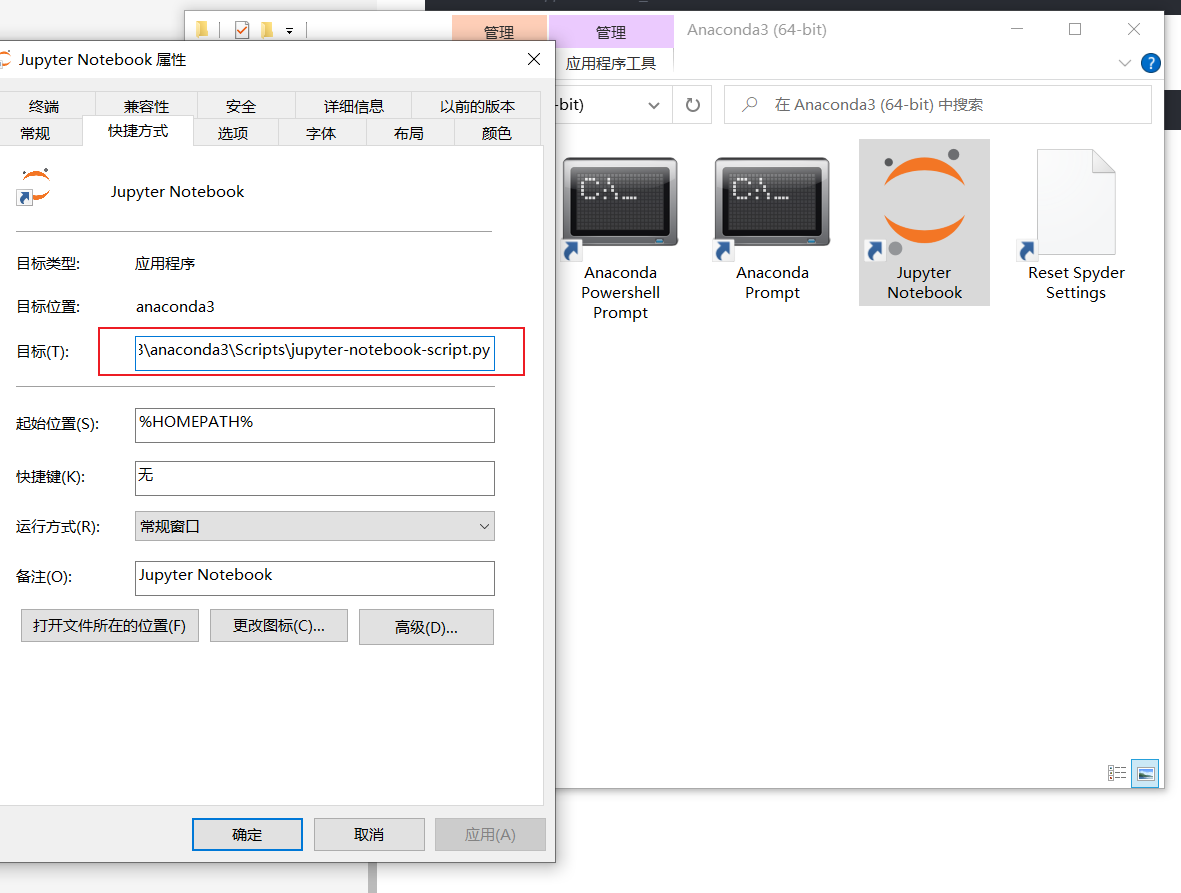
如何修改jupyter notebook默认打开路径
1、用jupyter notebook在其他位置打开自己的ipython项目: jupyter notebook是一个很好用的工具,可以保存运行结果,还可以给项目添加很多可视化操作与介绍文字。安装anaconda后,jupyter notebook就会自动安装,点开它会…...

【leetcode】数组排序
【leetcode】数组排序 task03 主要了解了数组中常见的排序方法: 1.常见数组排序方法 冒泡排序(Bubble Sort): 冒泡排序是一种简单的排序算法,它多次遍历数组,比较相邻的元素并交换它们,直到整…...
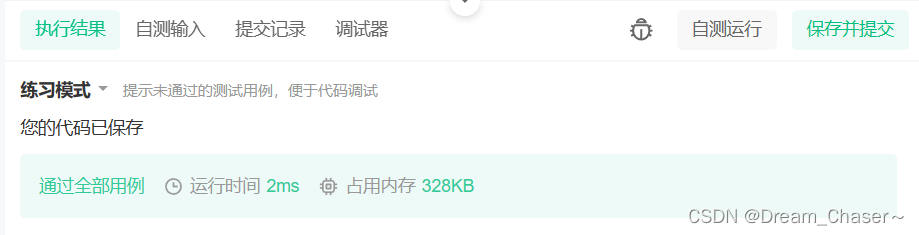
【C刷题训练营】第四讲(打好基础很重要)
前言: 大家好,这是c语言刷题训练营的第四讲,打好基础便于对c语言语法与算法思维的提高,感谢你的来访与支持! 💥🎈个人主页:Dream_Chaser~ 🎈💥 ✨✨刷题专栏…...

MySQL 某个字段存储不了内容
1. 原因 某个字段存储的内容过大 2. 解决 修改max_allowed_packet参数 max_allowed_packet参数是指mysql服务器端在一次传送数据包的过程当中最大允许的数据包大小。如果超过了设置的最大长度,则会数据库保持数据失败。 2.1 查询参数 show variables like %max…...
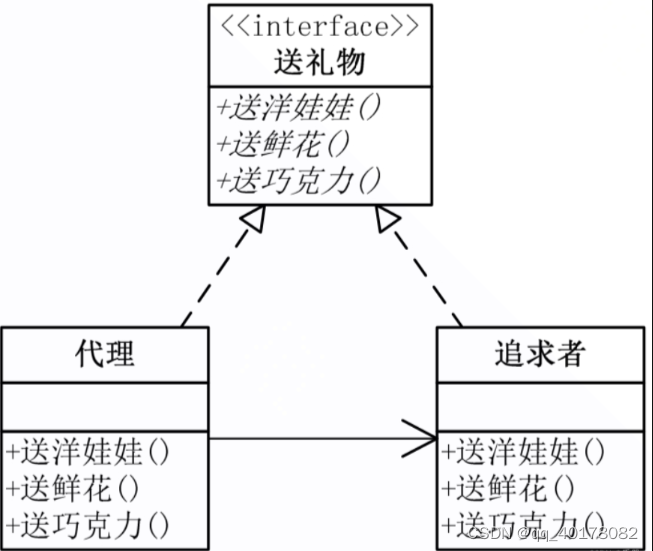
7.代理模式
1.UML 2.代码 #include <iostream> using namespace std;class Subject{ public:virtual void Request() 0; };class RealSubject:public Subject { public:virtual void Request(){cout << "RealSubject" << endl;} }; class Proxy:public Subj…...

单例模式的安全写法
要想知道怎么写单例模式,那么必须得知道什么是单例模式。单例模式是一种设计模式,它确保某个类只有一个实例,并且提供一个全局访问该实例的方法。单例模式不会创建实例副本,而是返回对已创建实例的引用。单例模式的创建可以分为两…...

牛客网SQL156
各个视频的平均完播率_牛客题霸_牛客网 方法一 select a.video_id,format(count(b.video_id)/count(a.video_id),3) 完播率 from (select uid,video_id,(end_time-start_time) 播放时长from tb_user_video_logwhere year(start_time)2021 or year(end_time)2021 ) a left joi…...
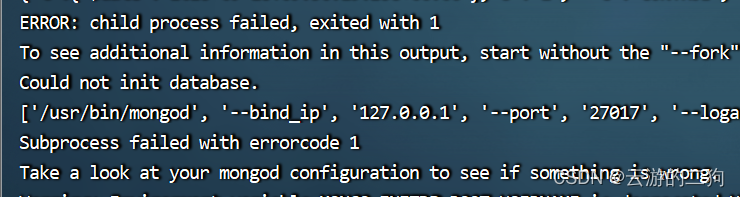
【MongoDB】docker部署社区版(一)
0、背景介绍 项目中使用MongoDB了,服务器挂掉,自己在本地搭一个试试。 1、版本选择 首先有社区版和和商业版。我选的是社区版。链接:https://hub.docker.com/r/mongodb/mongodb-community-server/tags 1.1、标签选择 看到标签有两个大类…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
