【数据结构】树的存储结构;树的遍历;哈夫曼树;并查集
欢~迎~光~临~^_^
目录
1、树的存储结构
1.1双亲表示法
1.2孩子表示法
1.3孩子兄弟表示法
2、树与二叉树的转换
3、树和森林的遍历
3.1树的遍历
3.1.1先根遍历
3.1.2后根遍历
3.2森林的遍历
3.2.1先序遍历森林
3.2.2中序遍历森林
4、树与二叉树的应用
4.1哈夫曼树
4.1.1概念
4.1.2构造哈夫曼树
4.1.3哈夫曼编码
4.1.4C语言实现哈夫曼树
4.2并查集编辑
4.2.1逻辑结构
4.2.2基本操作
4.2.3存储结构
4.2.4优化
1、树的存储结构

1.1双亲表示法
树的双亲表示法是一种简单的树结构表示方法,它在每个结点中存储了该结点的父节点信息。具体地,每个结点包含两部分信息,一部分是该结点的数据,另一部分是该结点的父节点的索引值。根结点没有父节点,通常用一个特定的值来表示。双亲表示法的优点是在访问任意结点的父节点时非常快,但是在查找任意结点的子节点时则需要遍历整棵树来确定其子节点。
例如,下面是一个有6个节点的树的双亲表示法的例子:
struct TreeNode {int data; // 节点数据int parent; // 父节点索引
};TreeNode tree[6]; // 定义一个有6个节点的树,每个节点包含数据和父节点索引两部分信息
tree[0].data = 1; // 第一个节点的数据是1,它是根节点,没有父节点
tree[1].data = 2; // 第二个节点的数据是2,它的父节点是根节点,其父节点索引为0
tree[1].parent = 0;
tree[2].data = 3; // 第三个节点的数据是3,它的父节点是根节点,其父节点索引为0
tree[2].parent = 0;
tree[3].data = 4; // 第四个节点的数据是4,它的父节点是第二个节点,其父节点索引为1
tree[3].parent = 1;
tree[4].data = 5; // 第五个节点的数据是5,它的父节点是第二个节点,其父节点索引为1
tree[4].parent = 1;
tree[5].data = 6; // 第六个节点的数据是6,它的父节点是第三个节点,其父节点索引为2
tree[5].parent = 2;1.2孩子表示法
树的孩子表示法是一种常用的树的存储方式,它的基本思想是:每个节点都存储它的孩子节点的指针(地址)。
相比于其他树的存储方式,孩子表示法的优点是:
-
能够较快地访问节点的孩子节点,因为每个节点都存储了它的孩子节点的指针;
-
孩子表示法的存储方式相对简单、直观易懂。
但是,孩子表示法也存在一些缺点:
-
孩子节点的数量不固定,因此存储时需要动态分配内存空间;
-
访问父节点比较麻烦,需要从根节点开始遍历整棵树才能找到父节点。
1.3孩子兄弟表示法
孩子兄弟表示法是一种树型数据结构中用于表示节点关系的方法,通常用于表示一个树或者一棵森林中的节点之间的关系。
在孩子兄弟表示法中,每个节点包含两个指针:一个指向该节点的第一个孩子节点,另一个指向该节点的下一个兄弟节点。因此,通过这两个指针可以遍历整棵树或森林中的节点,并找到它们的父节点、孩子节点和兄弟节点。
孩子兄弟表示法的主要优点是它能够有效地减少存储空间的使用,因为每个节点只需要存储两个指针,而不需要像其他表示方法那样存储父节点和所有孩子节点的指针。
然而,由于每个节点只存储了两个指针,因此在进行某些操作时,可能需要遍历整棵树或森林,这可能会导致效率较低。
2、树与二叉树的转换
将一棵树转换为二叉树的方法,可以选择先把树转换为森林,然后再对每棵树进行转换。转换的基本思路是:将每个节点的第一个孩子作为其左孩子,将兄弟节点作为其右孩子。
具体实现如下:
1. 首先对树进行先序遍历,从根节点开始遍历。
2. 对于每个节点,如果它有孩子节点,将其第一个孩子节点作为其左孩子。
3. 对于每个节点的兄弟节点,将其作为当前节点右孩子。
4. 对于所有没有孩子节点的节点,将其左孩子和右孩子都设为空。
5. 最终得到的结果是一棵二叉树。
将一棵二叉树转换为一棵树的方法,可以选择先把二叉树转换为森林,然后再将森林中的所有树合并为一棵树。具体实现如下:
1. 针对每个节点,将其左孩子作为其第一个孩子节点,将其右孩子的子树转换为其兄弟节点。
2. 对于每个节点,先将其所有孩子节点合并为一棵子树,然后将其所有兄弟节点依次加入这棵子树中。
3. 最终得到的结果是一棵树。
3、树和森林的遍历
3.1树的遍历
3.1.1先根遍历
树的先根遍历是一种树的遍历方式,先访问根节点,然后依次遍历其子节点,再依次遍历每个子节点的子树的根节点。
例如,对于下图所示的树:
A/ \B C/ / \
D E F先根遍历的顺序是:A -> B -> D -> C -> E -> F。
3.1.2后根遍历
树的后根遍历(也叫后序遍历)是指先访问一个节点的左子树和右子树,最后再访问该节点本身。具体的遍历顺序如下:
- 访问该节点的左子树
- 访问该节点的右子树
- 访问该节点本身
通常,可以使用递归或迭代算法实现树的后根遍历。递归的实现方式比较简单。
迭代的实现方式稍微复杂一些,需要借助栈来实现。具体的算法如下:
- 将根节点压入栈中
- 如果栈不为空,则取出栈顶节点
- 如果该节点没有左右子节点或者其左右子节点已经被访问过,则访问该节点并弹出
- 如果该节点有左右子节点且其左右子节点还未被访问,则将其右子节点和左子节点依次压入栈中,保证左右子节点先被访问
3.2森林的遍历
3.2.1先序遍历森林
先序遍历森林是指以任意一棵树的根节点为起点,按照先访问根节点,再依次访问子树的方式遍历整个森林。具体操作如下:
- 访问当前节点
- 依次以当前节点的子节点为根节点,重复进行上述操作
在实际操作中,可以采用递归或栈的方式实现先序遍历森林。以递归方式为例,实现代码如下:
void preOrderForest(Node* root) {if (root == nullptr) {return;}// 访问当前节点visit(root);// 依次遍历子树for (Node* child : root->children) {preOrderForest(child);}
}其中,Node代表树节点的数据结构,root表示当前节点,children表示当前节点的子节点列表,visit()表示访问节点的操作。
3.2.2中序遍历森林
森林的后序遍历是将森林中每个树的后序遍历序列依次拼接起来,得到的序列即为森林的后序遍历。
具体步骤如下:
- 对每棵树分别进行后序遍历。
- 将每棵树的后序遍历序列依次拼接起来,即可得到森林的后序遍历序列。
例如,对以下森林进行后序遍历:
B C D/ \ / \
E F G H首先分别对三棵树 B-EF、C、D-GH 进行后序遍历,得到它们的后序遍历序列:
B-EF的后序遍历序列为:E F B
C的后序遍历序列为:C
D-GH的后序遍历序列为:G H D
然后将它们依次拼接起来,得到森林的后序遍历序列:E F B C G H D
4、树与二叉树的应用
4.1哈夫曼树
4.1.1概念
哈夫曼树(Huffman Tree)是一种特殊的二叉树,它是一种最优二叉树,常用于数据压缩和编码中。哈夫曼树的构建过程是基于哈夫曼编码的原理,即将出现频率较高的字符用较短的编码,而出现频率较低的字符用较长的编码。哈夫曼树的构建过程是将每个字符作为一个节点,并将它们按照出现频率从小到大排序,然后将频率最小的两个节点合并成一个新的节点,其权值为两个节点的权值之和。重复这个过程,直到所有节点都被合并成为一个根节点为止。最后形成的这个根节点就是哈夫曼树的根节点。哈夫曼树的叶子节点表示原始数据中的字符,而路径上的0、1代表相应的比特位编码。哈夫曼树是一种满足最优化标准的树形结构,可以使编码后的数据更加紧凑,从而达到压缩数据的目的。

4.1.2构造哈夫曼树
哈夫曼树是一种带权路径长度最小的树,用于编码和数据压缩。构造哈夫曼树的过程如下:
- 将节点按权值从小到大排序,构造n个只含一个节点的二叉树,每个节点代表一个权值。
- 选择权值最小的两棵二叉树合并成一棵新二叉树,根节点的权值为这两棵二叉树的权值之和。
- 从已选的n棵二叉树中删除这两棵二叉树,将新的二叉树加入到集合中。
- 重复步骤2和步骤3,直到只剩下一棵二叉树,这棵树就是哈夫曼树。
4.1.3哈夫曼编码
将字符频次作为字符结点权值,构造哈夫曼树,即可得到哈夫曼编码,可用于数据压缩。
前缀编码:没有一个编码 是另一个编码的前缀
固定长度编码:每个字符用相等长度的二进制位表示
可变长度编码: 允许对不同字符用不等长的二进制位表示
哈夫曼编码的生成过程包括以下几个步骤:
- 统计每个字符在数据中出现的频率;
- 将每个字符和其对应的频率构建成一个叶子节点;
- 构建哈夫曼树,将每个节点按照频率从小到大排序,然后将相邻的两个节点合并成一个新节点,其频率为两个节点的频率之和。重复此过程,直到所有节点都合并为一个根节点;
- 给每个叶子节点分配一个编码,从根节点开始,向左走则编码为0,向右走则编码为1,直到到达叶子节点;
- 用每个字符的编码替换原始数据中相应的字符,从而得到压缩后的数据。
4.1.4C语言实现哈夫曼树
哈夫曼树是一种应用广泛的数据结构,用于有效地压缩数据。在C语言中,哈夫曼树的实现可以通过以下步骤完成:
1. 定义节点结构体
首先需要定义一个节点结构体,用于表示哈夫曼树中的每个节点。该结构体包含左子树、右子树、权值和字符等信息。
struct HuffmanNode {int weight; // 权值char ch; // 字符struct HuffmanNode *left; // 左子树struct HuffmanNode *right; // 右子树
};2. 定义比较函数
比较函数用于在构建哈夫曼树时对节点进行排序。该函数将根据节点的权值大小进行比较。
int cmp(const void *a, const void *b) {const struct HuffmanNode *node1 = a;const struct HuffmanNode *node2 = b;return node1->weight - node2->weight;
}3. 构建哈夫曼树
构建哈夫曼树的过程可以通过一些简单的步骤完成。首先需要将每个字符作为一个叶子节点插入到优先队列中,然后不断地取出队列中权值最小的两个节点,将它们合并成一个新节点,并将新节点插入到队列中。重复此过程,直到队列中只剩下一个根节点,此时构建的就是哈夫曼树。
struct HuffmanNode *buildHuffmanTree(const char *str) {// 统计字符出现的次数int count[256] = {0};for (int i = 0; i < strlen(str); i++) {count[str[i]]++;}// 将每个字符作为一个叶子节点插入到优先队列中int size = 0;struct HuffmanNode *nodes[256];for (int i = 0; i < 256; i++) {if (count[i] > 0) {nodes[size] = malloc(sizeof(struct HuffmanNode));nodes[size]->ch = (char)i;nodes[size]->weight = count[i];nodes[size]->left = NULL;nodes[size]->right = NULL;size++;}}// 构建哈夫曼树while (size > 1) {// 取出队列中权值最小的两个节点qsort(nodes, size, sizeof(struct HuffmanNode *), cmp);struct HuffmanNode *left = nodes[0];struct HuffmanNode *right = nodes[1];// 合并两个节点struct HuffmanNode *parent = malloc(sizeof(struct HuffmanNode));parent->ch = '\0';parent->weight = left->weight + right->weight;parent->left = left;parent->right = right;// 将新节点插入到队列中nodes[0] = parent;for (int i = 2; i < size; i++) {nodes[i - 1] = nodes[i];}size--;}return nodes[0];
}4. 遍历哈夫曼树
遍历哈夫曼树可以得到每个字符的编码,即通过左子树走一步为0,右子树走一步为1。在遍历过程中,需要记录下从根节点到当前节点的路径上的字符编码,以便后续使用。
void traverseHuffmanTree(struct HuffmanNode *node, char *code, int depth) {if (node->left == NULL && node->right == NULL) {// 叶子节点,输出编码printf("%c: %s\n", node->ch, code);} else {// 遍历左子树code[depth] = '0';traverseHuffmanTree(node->left, code, depth + 1);// 遍历右子树code[depth] = '1';traverseHuffmanTree(node->right, code, depth + 1);}
}5. 完整代码
将以上步骤整合起来,可以得到完整的C语言实现代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>struct HuffmanNode {int weight; // 权值char ch; // 字符struct HuffmanNode *left; // 左子树struct HuffmanNode *right; // 右子树
};int cmp(const void *a, const void *b) {const struct HuffmanNode *node1 = a;const struct HuffmanNode *node2 = b;return node1->weight - node2->weight;
}struct HuffmanNode *buildHuffmanTree(const char *str) {// 统计字符出现的次数int count[256] = {0};for (int i = 0; i < strlen(str); i++) {count[str[i]]++;}// 将每个字符作为一个叶子节点插入到优先队列中int size = 0;struct HuffmanNode *nodes[256];for (int i = 0; i < 256; i++) {if (count[i] > 0) {nodes[size] = malloc(sizeof(struct HuffmanNode));nodes[size]->ch = (char)i;nodes[size]->weight = count[i];nodes[size]->left = NULL;nodes[size]->right = NULL;size++;}}// 构建哈夫曼树while (size > 1) {// 取出队列中权值最小的两个节点qsort(nodes, size, sizeof(struct HuffmanNode *), cmp);struct HuffmanNode *left = nodes[0];struct HuffmanNode *right = nodes[1];// 合并两个节点struct HuffmanNode *parent = malloc(sizeof(struct HuffmanNode));parent->ch = '\0';parent->weight = left->weight + right->weight;parent->left = left;parent->right = right;// 将新节点插入到队列中nodes[0] = parent;for (int i = 2; i < size; i++) {nodes[i - 1] = nodes[i];}size--;}return nodes[0];
}void traverseHuffmanTree(struct HuffmanNode *node, char *code, int depth) {if (node->left == NULL && node->right == NULL) {// 叶子节点,输出编码printf("%c: %s\n", node->ch, code);} else {// 遍历左子树code[depth] = '0';traverseHuffmanTree(node->left, code, depth + 1);// 遍历右子树code[depth] = '1';traverseHuffmanTree(node->right, code, depth + 1);}
}int main() {char str[] = "hello world";struct HuffmanNode *root = buildHuffmanTree(str);char code[256];traverseHuffmanTree(root, code, 0);return 0;
}4.2并查集
4.2.1逻辑结构
并查集是一种用于处理集合并、查找和判定两个元素是否在同一集合中的数据结构。它的基本操作有初始化、查找、合并等。
并查集的逻辑结构通常由一个数组和若干个操作函数构成。数组中每个元素对应一个集合,它的值表示当前元素所在集合的根节点编号。在初始化时,每个元素都是一个单独的集合,即它的根节点编号为自身。查找操作用于找到某个元素所在集合的根节点编号,它通过递归查找父节点的方式实现路径压缩。合并操作用于合并两个集合,它将其中一个集合的根节点编号设为另一个集合的根节点编号,从而实现两个集合的合并。
并查集的优点是可以快速地进行集合合并和查找,时间复杂度为O(log n)。它常用于解决连通性问题,如判断图是否连通、求无向图的连通分量等。
4.2.2基本操作
并查集是一种用于维护集合的数据结构,通常支持以下操作:
1. MakeSet(x):创建一个新的集合,其中只包含元素 x。
2. Union(x, y):将包含元素 x 和 y 的两个集合合并成一个新集合。
3. Find(x):查找元素 x 所在的集合,并返回该集合的代表元素。
通常还会有一些额外的操作,例如:
4. SizeOf(x):返回包含元素 x 的集合中元素的数量。
5. IsConnected(x, y):判断元素 x 和 y 是否在同一个集合中。
6. CountSets():返回当前并查集中集合的数量。
在实现并查集的过程中,常见的数据结构有数组和树。使用数组实现时,每个元素的值表示其父节点的索引,根节点的父节点值为-1。使用树实现时,每个节点的父节点指向它的父节点。
在 Find(x) 操作中,可以通过递归或迭代的方式将元素 x 所在的集合中的所有元素都指向该集合的代表元素,以达到路径压缩的效果,加快后续对同一集合的 Find 操作的速度。
在 Union(x, y) 操作中,可以选择将一个集合的根节点作为另一个集合的子树,或者将两个集合的根节点合并成一个新的集合。通常建议采用按秩合并和路径压缩(即将深度较浅的树作为深度较深的树的子树)的算法,以保证并查集操作的时间复杂度为 O(α(n)),其中 α(n) 是反阿克曼函数的逆函数,增长极其缓慢,因此在实际应用中可以认为它是一个常数。
4.2.3存储结构
并查集的存储结构可以采用数组或树形结构。常用的是采用树形结构进行存储。
对于每个元素x,都有一个对应的父结点parent[x],如果x是根结点,则parent[x]=-1。在初始化时,可以将每个元素看成一个独立的集合,即其父节点为其自身。随着不断的合并操作,两个元素所在的集合就会合并成为一棵树。
在合并两个集合时,需要将其中一个集合的根节点的父结点设置为另一个集合的根节点。此时,其中一个树就成为另一个树的子树。
通过路径压缩的技巧,可以使得树形结构更加扁平化,从而提高查询效率。具体而言,在查找某个元素所在的集合时,可以沿途将路径上的节点的父节点都设置为该集合的根节点,从而将树的高度降低,进一步提高查询效率。
4.2.4优化
并查集是一种数据结构,用于解决集合的合并和查询问题。在对大量数据进行操作时,为了提高效率,需要对并查集进行优化。
以下是一些并查集的优化方法:
1. 路径压缩:在 find 操作时,将路径上的所有节点都直接连接到根节点上,从而缩短查找路径的长度,减少操作的时间复杂度。
2. 按秩合并:在合并两个集合时,将高度低的集合合并到高度高的集合中,从而保持树的平衡,减少操作的时间复杂度。
3. 路径分裂:在路径压缩时,不仅将路径上的所有节点直接连接到根节点上,还可以将路径上的每个节点的父节点指向其祖先节点的子节点,从而减少路径压缩导致的树的深度增加。
4. 路径减半:在路径压缩时,不仅将路径上的所有节点直接连接到根节点上,还可以将路径上每隔一个节点的父节点指向其祖先节点的父节点,从而减少路径压缩导致的树的深度增加。
🤞❤️🤞❤️🤞❤️树与二叉树的知识点总结就到这里啦,如果对博文还满意的话,劳烦各位看官动动“发财的小手”留下您对博文的赞和对博主的关注吧🤞❤️🤞❤️🤞❤️

相关文章:

【数据结构】树的存储结构;树的遍历;哈夫曼树;并查集
欢~迎~光~临~^_^ 目录 1、树的存储结构 1.1双亲表示法 1.2孩子表示法 1.3孩子兄弟表示法 2、树与二叉树的转换 3、树和森林的遍历 3.1树的遍历 3.1.1先根遍历 3.1.2后根遍历 3.2森林的遍历 3.2.1先序遍历森林 3.2.2中序遍历森林 4、树与二叉树的应用 4.1哈夫曼树…...
CSS选择器练习小游戏
请结合CSS选择器练习小游戏进行阅读(网页的动态效果是没有办法通过静态图片展示的) 网址:请点击 有些题有多种答案,本文就不一一列出了 第一题 答案:plate第二题 答案:bento第三题 答案:#fa…...
Python运算符、函数与模块和程序控制结构
给我家憨憨写的python教程 ——雁丘 Python运算符、函数与模块和程序控制结构 关于本专栏一 运算符1.1 位运算符1.1.1 按位取反1.1.2 按位与1.1.3 按位或1.1.4 按位异或1.1.5 左移位 1.2 关系运算符1.3 运算顺序1.4 运算方向 二 函数与模块2.1 内建函数2.2 库函数2.2.1 标准库…...
微服务保护-Sentinel
初识Sentinel 雪崩问题及解决方案 雪崩问题 微服务中,服务间调用关系错综复杂,一个微服务往往依赖于多个其它微服务。 如图,如果服务提供者I发生了故障,当前的应用的部分业务因为依赖于服务I,因此也会被阻塞。此时&a…...

Doris 导出表结构或数据
MYSQLDUMP 导出表结构或数据 Doris 在0.15 之后的版本已经支持通过mysqldump 工具导出数据或者表结构 使用示例 导出 导出 test 数据库中的 table1 表:mysqldump -h127.0.0.1 -P9030 -uroot --no-tablespaces --databases test --tables table1导出 test 数…...

SELECT * from t_user where user_id = xxx,可以从那几个点去优化这句sql
优化SQL查询可以从以下几个方面入手: 1. 索引优化:通过为查询涉及的列添加合适的索引,可以提高查询的效率。在该SQL语句中, user_id 列被用作查询条件,可以为 user_id 列创建一个索引。 2. 避免使用 SELECT *…...

解决报错 java.lang.IllegalArgumentException: Cannot format given Object as a Date
报错原因:我们在SimpleDateFormat.format转化时间格式的时候,传入的值无法转换成date而报的错 我的代码大概就是下面这种 LocalDate now LocalDate.now();String format1 new SimpleDateFormat("yyyy-MM-dd").format(now); 发现SimpleDateF…...
【Git】03-GitHub
文章目录 1. GitHub核心功能2. GitHub搜索项目3. GitHub搭建个人博客4. 团队项目创建5. git工作流选择5.1 需要考虑的因素5.2 主干开发5.2 Git Flow5.3 GitHub Flow5.4 GitLab Flow(带生产分支)5.4 GitLab Flow(带环境分支)5.4 GitLab Flow(带发布分支) 6. 分支集成策略7. 启用…...

Java手写最短路径算法和案例拓展
Java手写最短路径算法和案例拓展 1. 算法手写的必要性 在实际开发中,经常需要处理图的最短路径问题。虽然Java提供了一些图算法库,但手写最短路径算法的必要性体现在以下几个方面: 理解算法原理:手写算法可以帮助我们深入理解最…...

深度学习实战51-基于Stable Diffusion模型的图像生成原理详解与项目实战
大家好,我是微学AI,今天给大家介绍一下深度学习实战51-基于Stable Diffusion模型的图像生成原理详解与项目实战。大家知道现在各个平台发的漂亮小姐姐,漂亮的图片是怎么生成的吗?这些生成的底层原理就是用到了Stable Diffusion模型。Stable Diffusion是一种基于深度学习的图…...
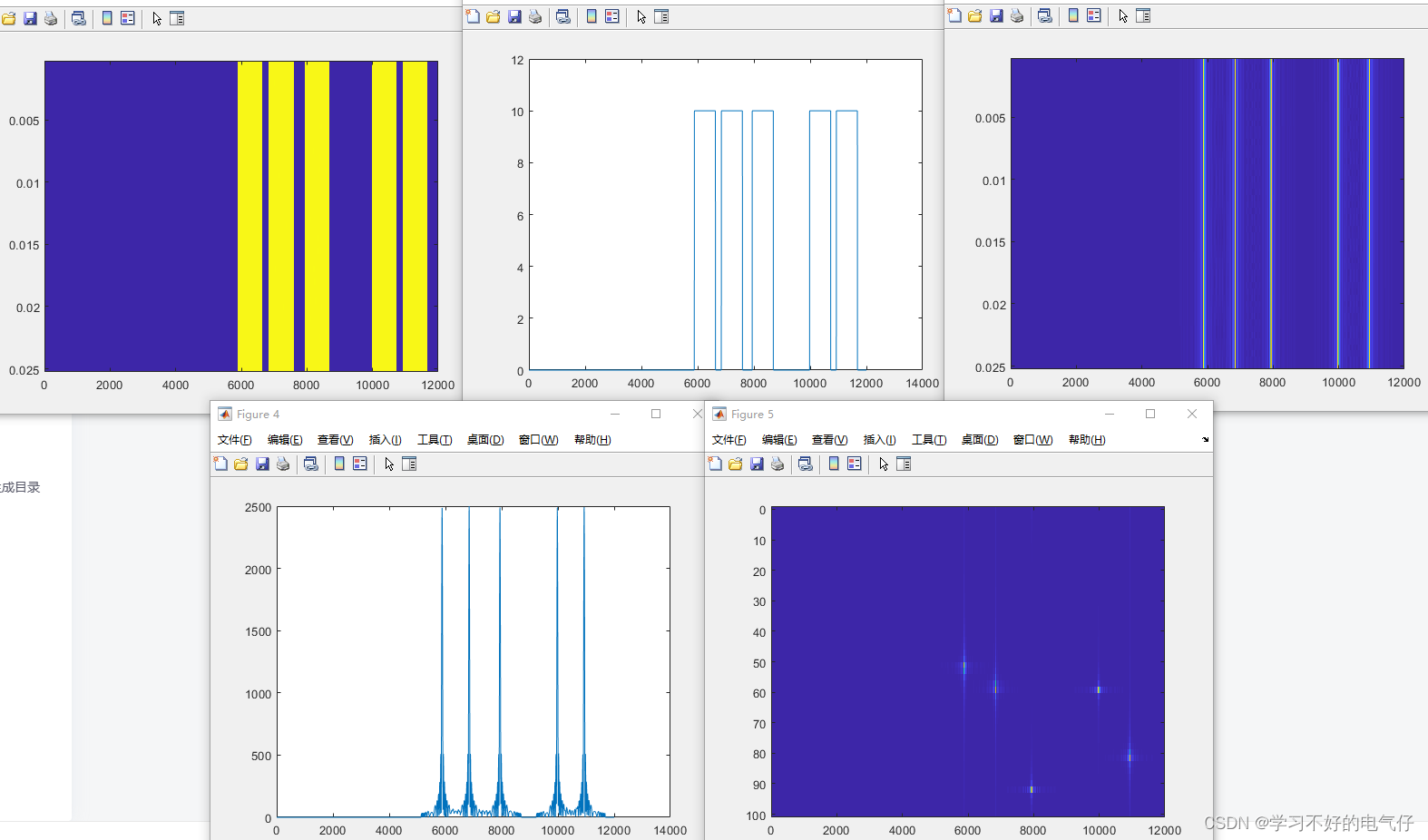
基于matlab实现的多普勒脉冲雷达回波仿真
完整程序: clear all;clc;close all; fc3e9; %载波频率 PRF2000; Br5e6; %带宽 fs10*Br; %采样频率 Tp5e-6; %脉宽 KrBr/Tp; %频率变化率 c3e8; %光速 lamda…...

Linux服务器中安装Anaconda+Tensorflow+Keras
Anaconda安装 从https://repo.anaconda.com/archive/查看你需要下载的Anaconda版本,例如2020.11的x86_64(uname -a 查看linux框架)版下载Anaconda到linux服务器, wget https://repo.anaconda.com/archive/Anaconda3-2020.11-Li…...

ubuntu+.net6+docker 应用部署教程
先期工作 1、本地首先安装 Docker Desktop 2、本地装linux in windows 3、生成镜像 后期工作 1、云服务器部署 生成镜像方法 1、生成Dockerfile配置文件 开发工具visual studio 2022 如果项目已经存在,可以选中项目,右键点击->选择添加Docker…...

Spring常见面试题总结
什么是Spring Spring是一个轻量级Java开发框架,目的是为了解决企业级应用开发的业务逻辑层和其他各层的耦合问题,以提高开发效率。它是一个分层的JavaSE/JavaEE full-stack(一站式)轻量级开源框架,为开发Java应用程序…...
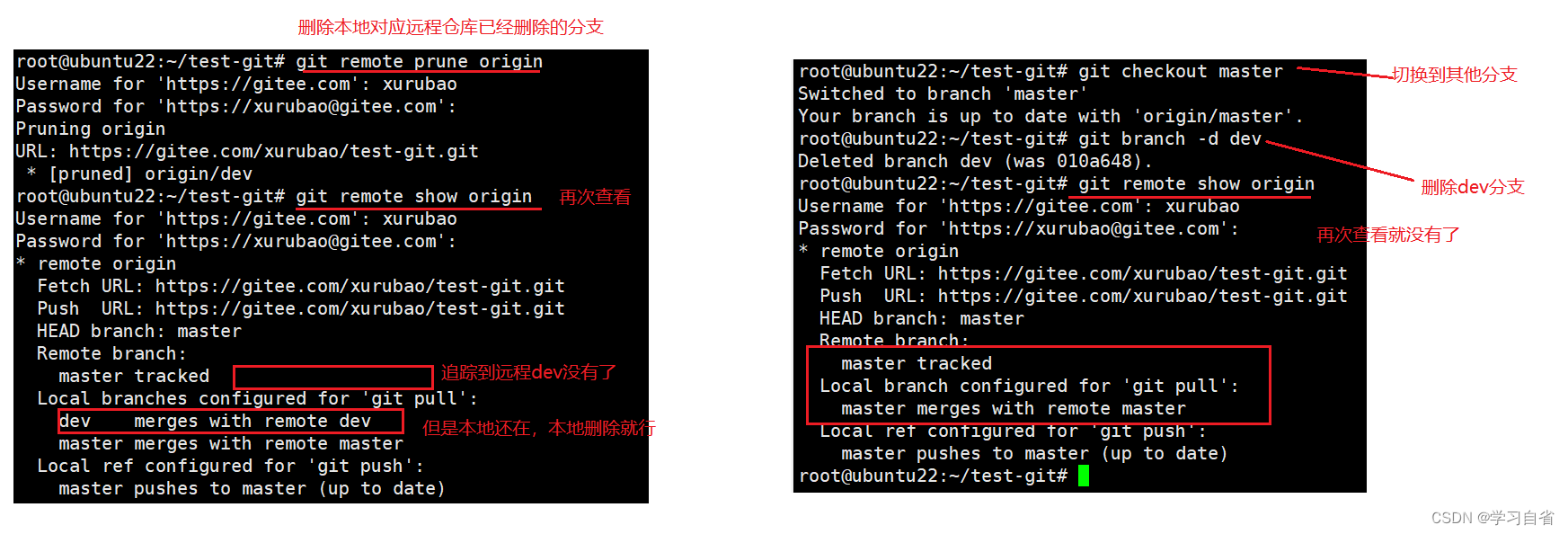
Git全套命令使用
日升时奋斗,日落时自省 目录 1、Git安装 1.1、创建git本地仓库 1.2、配置Git 1.3、认识Git内部区分 2、Git应用操作 2.1、添加文件 2.2、查看日志 2.3、查看修改信息 2.4、查看添加信息 3、版本回退 4、撤销修改 4.1、工作区撤销 4.2、已经add…...
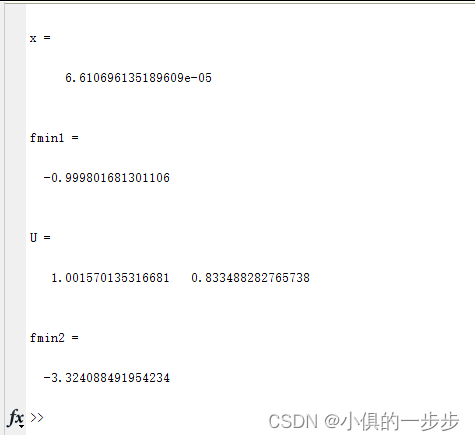
【陕西理工大学-数学软件实训】数学实验报告(8)(数值微积分与方程数值求解)
目录 一、实验目的 二、实验要求 三、实验内容与结果 四、实验心得 一、实验目的 1. 掌握求数值导数和数值积分的方法。 2. 掌握代数方程数值求解的方法。 3. 掌握常微分方程数值求解的方法。 二、实验要求 1. 根据实验内容,编写相应的MATLAB程序,…...

Vue3为什么推荐使用ref而不是reactive
为什么推荐使用ref而不是reactive reactive本身具有很大局限性导致使用过程需要额外注意,如果忽视这些问题将对开发造成不小的麻烦;ref更像是vue2时代option api的data的替代,可以存放任何数据类型,而reactive声明的数据类型只能是对象; 先抛出结论,再详细说原因:非必要不用rea…...

JavaScript函数this指向
一、this的指向规则 1.this到底指向什么呢? 我们先来看一个让人困惑的问题: 定义一个函数,我们采用三种不同的方式对它进行调用,它产生了三种不同的结果 // 定义函数 function foo(name) {console.log("foo函数:", …...
Java的序列化
写在前面 本文看下序列化和反序列化相关的内容。 源码 。 1:为什么,什么是序列化和反序列化 Java对象是在jvm的堆中的,而堆其实就是一块内存,如果jvm重启数据将会丢失,当我们希望jvm重启也不要丢失某些对象ÿ…...
)
计算机二级python简单应用题刷题笔记(一)
计算机二级python简单应用题刷题笔记(一) 1、词频统计:键盘输入一组我国高校所对应的学校类型,以空格分隔,共一行。2、找最大值、最小值、平均分:键盘输入小明学习的课程名称及考分等信息,信息间…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

