LeetCode 332. Reconstruct Itinerary【欧拉回路,通路,DFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
- 例如,行程
["JFK", "LGA"]与["JFK", "LGB"]相比就更小,排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次 。
示例 1:
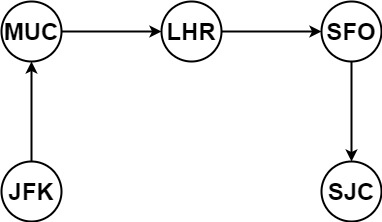
输入:tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]
输出:["JFK","MUC","LHR","SFO","SJC"]
示例 2:

输入:tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出:["JFK","ATL","JFK","SFO","ATL","SFO"]
解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ,但是它字典排序更大更靠后。
提示:
1 <= tickets.length <= 300tickets[i].length == 2fromi.length == 3toi.length == 3fromi和toi由大写英文字母组成fromi != toi
本题和「753. 破解保险箱」类似,是力扣平台上为数不多的求解欧拉回路 / 欧拉通路的题目。
我们化简本题题意:给定一个 O ( n ) O(n) O(n) 个点 O ( m ) O(m) O(m) 条边的图,要求从指定的顶点出发,经过所有的边恰好一次(可以理解为给定起点的「一笔画」问题),使得路径的字典序最小。这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义:
- 通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路;
- 通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路;
- 具有欧拉回路的无向图称为欧拉图;
- 具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。
因为本题保证至少存在一种合理的路径,也就告诉了我们,这张图是一个欧拉图或者半欧拉图。我们只需要输出这条欧拉通路的路径即可。如果没有保证至少存在一种合理的路径,我们需要判别这张图是否是欧拉图或者半欧拉图,具体地:
- 对于无向图 G G G , G G G 是欧拉图当且仅当 G G G 是连通的且没有奇度顶点。
- 对于无向图 G G G , G G G 是半欧拉图当且仅当 G G G 是连通的且 G G G 中恰有 0 0 0 个或 2 2 2 个奇度顶点。
- 对于有向图 G G G , G G G 是欧拉图当且仅当 G G G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
- 对于有向图 G G G , G G G 是半欧拉图当且仅当:
- 如果将 G G G 中的所有有向边退化为无向边时,那么 G G G 的所有顶点属于同一个强连通分量;
- 最多只有一个顶点的出度与入度差为 1 1 1 ;
- 最多只有一个顶点的入度与出度差为 1 1 1 ;
- 所有其他顶点的入度和出度相同。
让我们考虑下面的这张图:
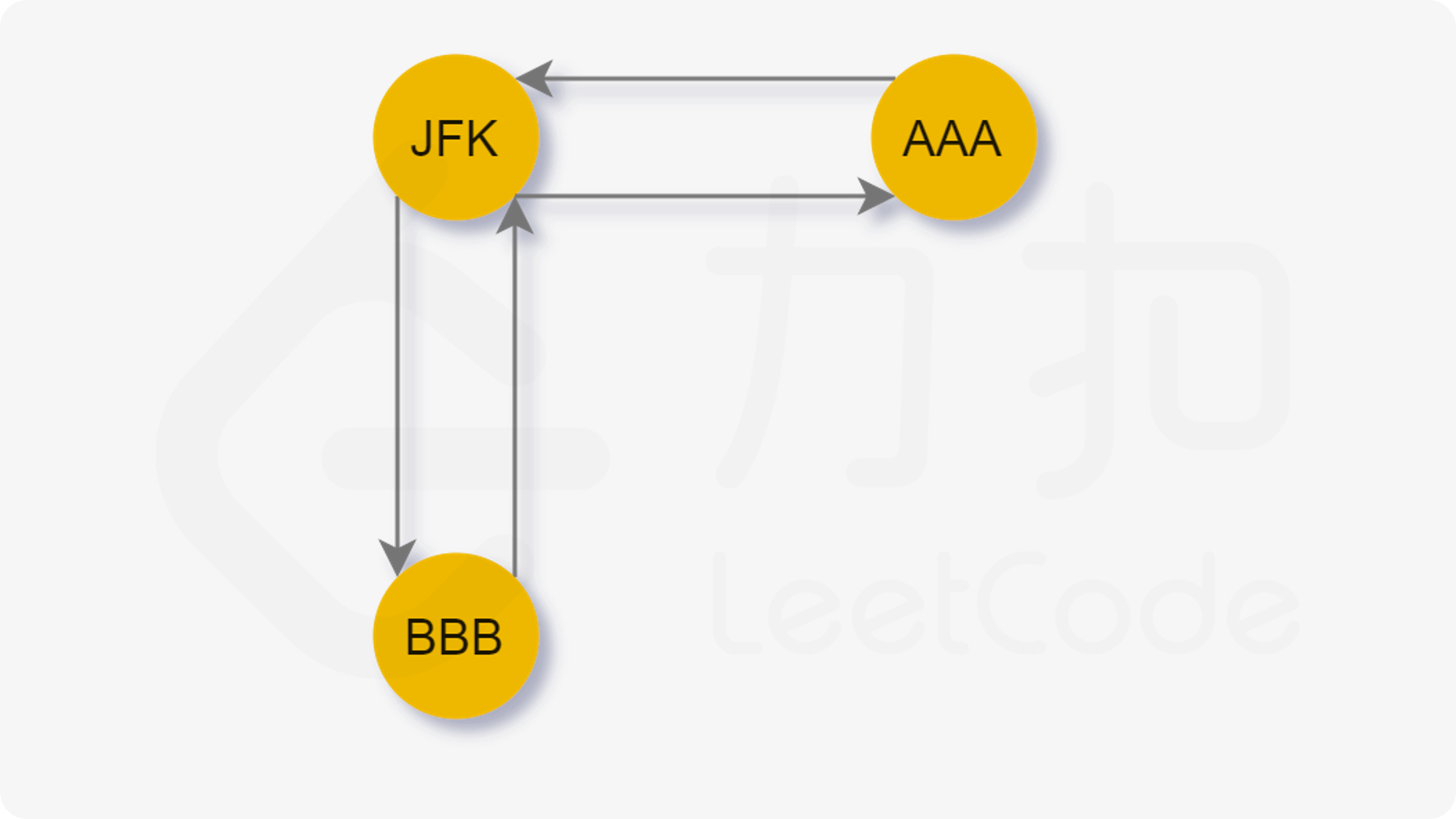
我们从起点 J F K JFK JFK 出发,合法路径有两条:
- J F K → A A A → J F K → B B B → J F K JFK→AAA→JFK→BBB→JFK JFK→AAA→JFK→BBB→JFK
- J F K → B B B → J F K → A A A → J F K JFK→BBB→JFK→AAA→JFK JFK→BBB→JFK→AAA→JFK
既然要求字典序最小,那么我们每次应该贪心地选择当前节点所连的节点中字典序最小的那一个,并将其入栈。最后栈中就保存了我们遍历的顺序。
为了保证我们能够快速找到当前节点所连的节点中字典序最小的那一个,我们可以使用优先队列存储当前节点所连到的点,每次我们 O ( 1 ) O(1) O(1) 地找到最小字典序的节点,并 O ( log m ) O(\log m) O(logm) 地删除它。
然后我们考虑一种特殊情况:
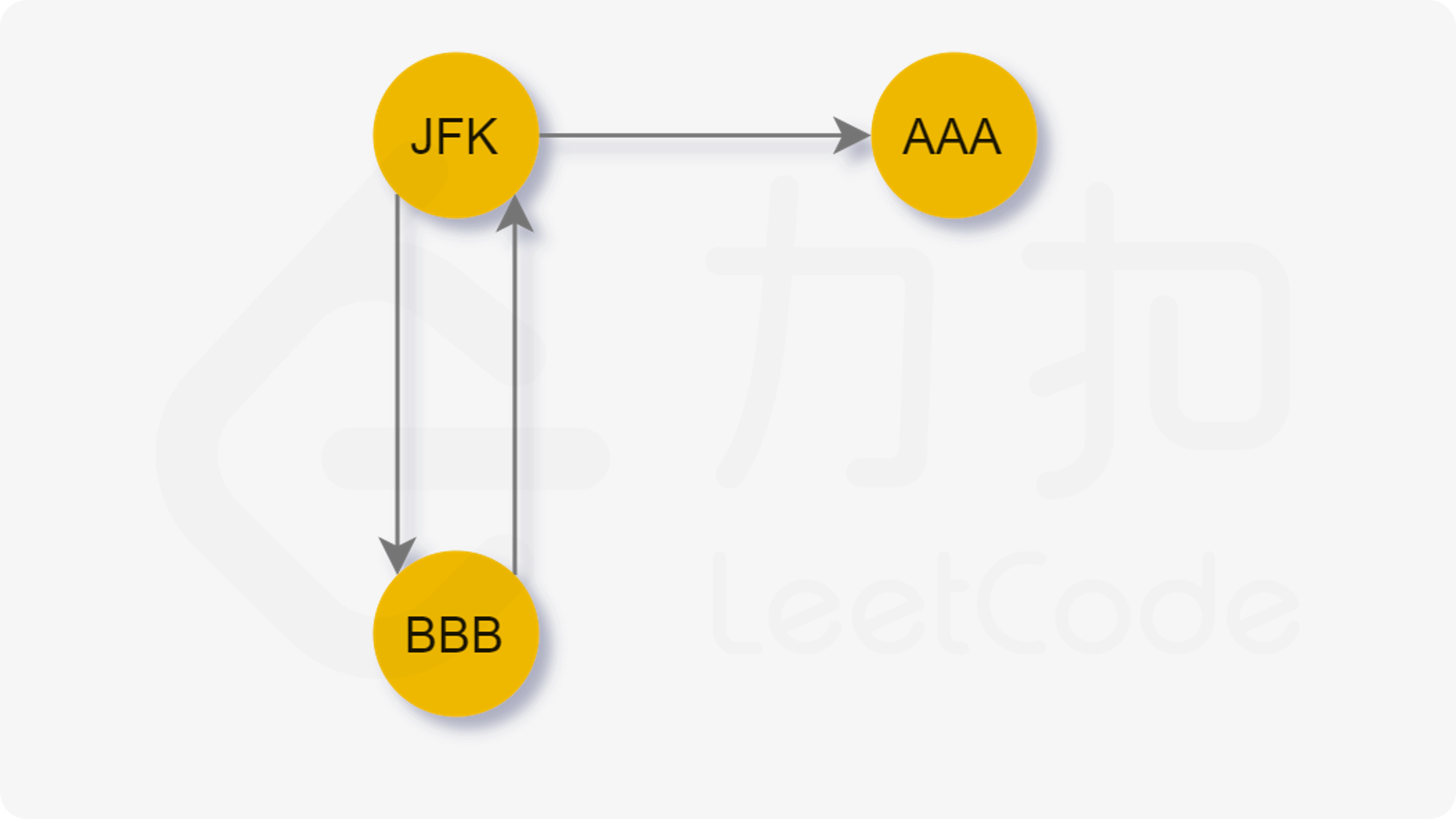
当我们先访问 A A A AAA AAA 时,我们无法回到 J F K JFK JFK,这样我们就无法访问剩余的边了。也就是说,当我们贪心地选择字典序最小的节点前进时,我们可能先走入「死胡同」,从而导致无法遍历到其他还未访问的边。于是我们希望能够遍历完当前节点所连接的其他节点后再进入「死胡同」。
注意对于每一个节点,它只有最多一个「死胡同」分支。依据前言中对于半欧拉图的描述,只有那个入度与出度差为 1 1 1 的节点会导致死胡同。
解法 H i e r h o l z e r Hierholzer Hierholzer 算法
H i e r h o l z e r Hierholzer Hierholzer 算法用于在连通图中寻找欧拉路径,其流程如下:
- 从起点出发,进行深度优先搜索。
- 每次沿着某条边从某个顶点移动到另外一个顶点时,都需要删除这条边。
- 如果没有可移动的路径,则将所在节点加入到栈中,并返回。
当我们顺序地考虑该问题时,我们也许很难解决该问题,因为我们无法判断当前节点的哪一个分支是「死胡同」分支。不妨倒过来思考。我们注意到只有那个入度与出度差为 1 1 1 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点——对于当前节点而言,走入它的每一个非「死胡同」分支进行深度优先搜索,都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。我们可以改变入栈的规则,当遍历完一个节点所连的所有节点后,才将该节点入栈(即逆序入栈),也就是说当前节点的死胡同分支始终优先于其他非「死胡同」分支入栈。
这样就能保证我们可以「一笔画」地走完所有边,且最终的栈中逆序地保存了「一笔画」的结果。我们只要将栈中的内容反转,即可得到答案。
class Solution {
public:unordered_map<string, priority_queue<string, vector<string>, std::greater<string>>> vec;vector<string> stk;void dfs(const string& curr) {while (vec.count(curr) && vec[curr].size() > 0) {string tmp = vec[curr].top();vec[curr].pop();dfs(move(tmp));}stk.emplace_back(curr);}vector<string> findItinerary(vector<vector<string>>& tickets) {for (auto& it : tickets) {vec[it[0]].emplace(it[1]);}dfs("JFK"); // JFK要么是欧拉回路的一点,要么是欧拉通路的起点 reverse(stk.begin(), stk.end());return stk;}
};
复杂度分析:
- 时间复杂度: O ( m log m ) O(m \log m) O(mlogm) ,其中 O ( m ) O(m) O(m) 是边的数量。对于每一条边我们需要 O ( log m ) O(\log m) O(logm) 地删除它,最终的答案序列长度为 m + 1 m+1 m+1 ,而与 O ( n ) O(n) O(n) 无关。
- 空间复杂度: O ( m ) O(m) O(m) ,其中 O ( m ) O(m) O(m) 是边的数量。我们需要存储每一条边。
相关文章:

LeetCode 332. Reconstruct Itinerary【欧拉回路,通路,DFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
236. 二叉树的最近公共祖先 Python
文章目录 一、题目描述示例 1示例 2示例 3 二、代码三、解题思路 一、题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满…...

WPF中DataGrid控件绑定数据源
步骤 创建数据源:首先,我们需要创建一个数据源,可以是一个集合(如List、ObservableCollection等),也可以是一个DataTable对象。数据源中的每个元素代表一行数据。 设置DataGrid的ItemsSource属性ÿ…...

Linux arm64 set_memory_ro/rw函数
文章目录 一、函数简介1.1 简介1.2 change_memory_common1.3 __change_memory_common 二、apply_to_page_range函数2.1 apply_to_page_range2.2 apply_to_p4d_range2.3 apply_to_pud_range2.4 apply_to_pmd_range2.5 apply_to_pte_range 三、hook系统调用参考资料 一、函数简介…...
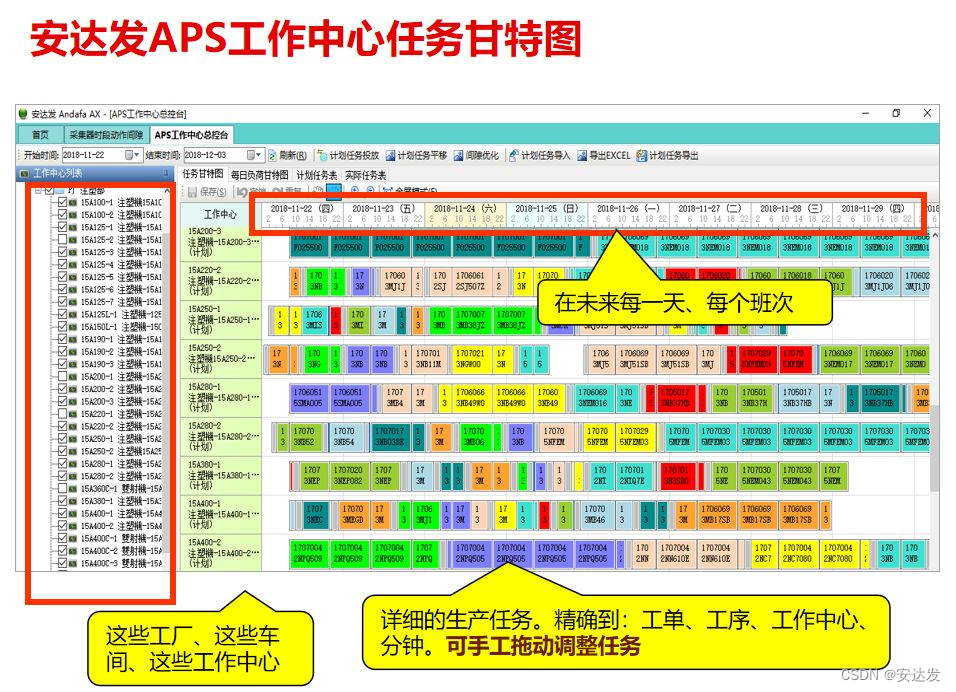
安达发|APS排单软件中甘特图的应用
近几年来,企业对生产效率和管理水平的要求越来越高。为了提高生产效率,降低生产成本,许多企业开始引入先进的生产计划与调度系统(APS),实现生产过程的自动化、智能化管理。APS排产软件是一种能够根据企业的…...
快速上手Linux基础开发工具
目录 软件包管理器 概念理解 用法示例 - 以yum为例 vim 模式的切换 常用操作 插件和配置 gcc/g gdb make / makefile 软件包管理器 概念理解 在Linux下安装软件的话,一个比较原始的办法是下载程序的源代码,然后进行编译,进而得到…...
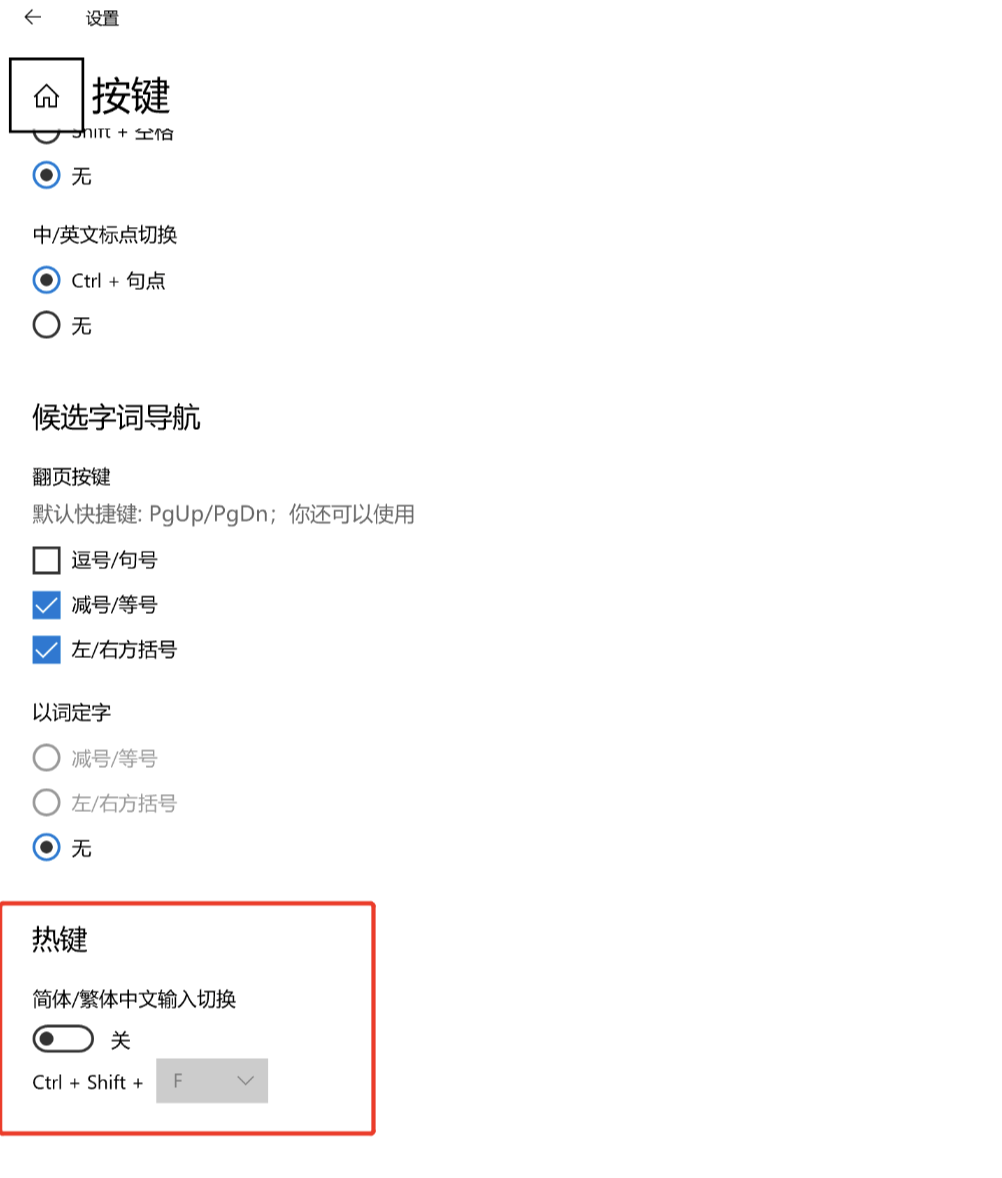
【开发工具】idea 的全局搜索快捷键(Ctrl+shift+F)失效
文章目录 前言1. 取消 输入法的快捷键(推荐使用)2.更改 idea的快捷键3. 热键占用总结 前言 当你发现在idea 中看到用于全局搜索的快捷键就是 CtrlshiftF,可是怎么按都不管用的时候,你就不要再执着于自己的操作继续狂点电脑按键了…...

港联证券:“火箭蛋”来袭 蛋价涨势能否延续?
上个交易周(9月11日至15日),鸡蛋期货商场呈现了意想不到的涨势。9月15日,鸡蛋期货多个合约大涨,其中2310合约涨超5.6%,主力合约2311盘中两度触及涨停,最终收涨6%。业内人士以为,鸡蛋…...
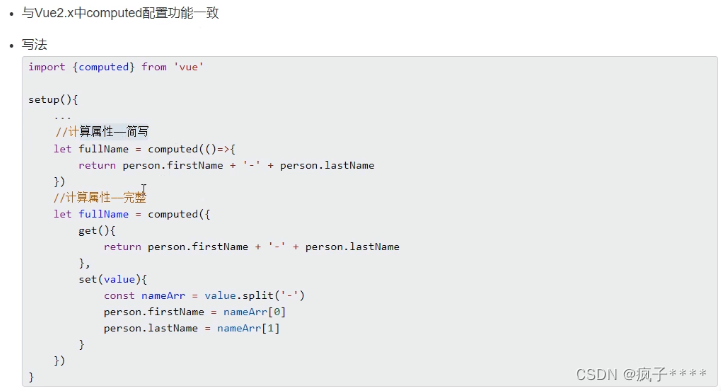
Vue3_vite
使用Vue-cli创建 使用vite创建 Composition API 组合API setup 1.Vue3中的一个新的配置项,值为一个函数 2.可以将组件中所用到的数据,方法等配置在setup中. 3.setup函数的两种返回值 3.1若返回一个对象,则对象中的属性,方法,在模板中均可以直接使用. 3.2若返回一个渲染函数…...

python-字符串去掉空格的常见方法
python提供了去掉字符串空格的方法,可以满足大部分需求。 但在实际应用中,还需要灵活借助python其他方法,来实现字符串空格的删除。 比如,去掉字符串的全部空格、字符串连续空格保留一个等,都需要结合其他的方法来实现…...

如何写出一个成熟的线上线下结合的营销方案?
分享一下咱们案例库里策划的一个线上线下结合的活动的案例。 这个活动是为了推广一个新品牌,增加品牌知名度和用户粘性。 你可以根据以下几个要点来进行活动策划: 1、目标: 让目标用户了解并喜欢新品牌,激发用户参与和分享&am…...

Vc - Qt - “扩张“的窗口
该示例演示了一个"扩张的窗口",主窗口的布局为水平布局,内置两个子窗口,采用定时器设置左边窗口的宽度,达到控制"扩张"的目的。 #include <QApplication> #include <QWidget> #include <QHBox…...
vue学习-02vue入门之组件
删除Vue-cli预设 在用户根目录下(C:\Users\你的用户名)这个地址里有一个.vuerc 文件,修改或删除配置 组件 Props(组件之间的数据传递) Prop 的大小写 (camelCase vs kebab-case)不敏感Prop 类型: String Number Boolean Array Object Date Function Symbol传递静态或动态 Pr…...
解决Pycharm使用Conda激活环境失败的问题
Q:公司电脑终端使用powershell来激活conda环境时报错? 同时手动打开powershell报"profile.ps1” 无法被加载的错误 A: 1,手动打开powershell,设置管理员打开 2,打开powershell 打开 PowerShell 终端,并输入以下命令:Get-ExecutionPo…...
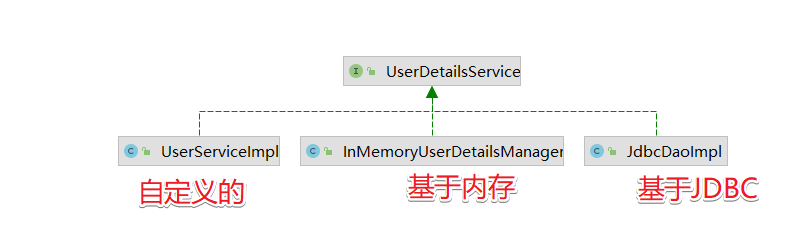
SpringSecurity 核心组件
文章目录 SpringSecurity 结构组件:SecurityContextHolder组件:Authentication组件:UserDetailsService组件:GrantedAuthority组件总结 SpringSecurity 结构 在SpringSecurity中的jar分为4个,作用分别为 jar作用spri…...
【Vue】快速入门和生命周期
目录 前言 一、vue的介绍 1. Vue.js是什么? 2. 库和框架的区别 3.基本概念和用法: 二、MVVM的介绍 1. 什么是MVVM? 2. MVVM的组成部分 3. MVVM的工作流程 4. MVVM的优势 5. MVVM的应用场景 三、vue实例 1.模板语法: …...

JVM架构和内存管理优化
Java虚拟机(JVM)是Java编程语言的核心组件,负责执行Java字节码并提供运行时环境,使得Java程序可以在不同的平台上运行。了解JVM的工作原理和内存管理对于优化代码性能和理解Java的内存管理和垃圾收集机制非常重要。在本文中&#…...
C语言——贪吃蛇小游戏
目录 一、ncurse 1.1 为什么需要用ncurse: 1.2 ncurse的输入输出: 1.2.1 如何使用ncurse: 1.2.2 编译ncurse的程序: 1.2.3 测试输入一个按键ncurse的响应速度: 1.3 ncurse上下左右键获取: 1.3.1 如…...

PHP8中获取并删除数组中第一个元素-PHP8知识详解
我在上一节关于数组的教程,讲的是在php8中获取并删除数组中最后一个元素,今天分享的是相反的:PHP8中获取并删除数组中第一个元素。 回顾一下昨天的知识,array_pop()函数将返回数组的最后一个元素,今天学习的是使用arr…...
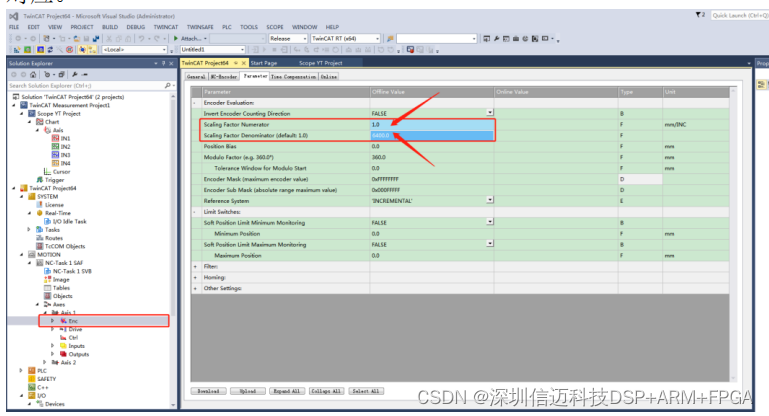
EtherCAT 总线型 4 轴电机控制卡解决方案
技术特点 支持标准 100M/s 带宽全双工 EtherCAT 总线网络接口及 CoE 通信协议一 进一出(RJ45 接口),支持多组动态 PDO 分组和对象字典的自动映射,支持站 号 ID 的自动设置与保存,支持 SDO 的电机参数设置与…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
