1462. 课程表 IV
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:Floyd传递闭包
- 方法二:拓扑排序
- 思考
- 写在最后
Tag
【拓扑排序】【传递闭包】【并查集】【数组】
题目来源
1462. 课程表 IV

题目解读
给你一个表示课程先决条件的数组 prerequisites,prerequisites[i] = [a, b] 表示在学习课程 b 之前要先学习课程 a,课程 a 是 b 的直接先决条件。如果课程 a 是课程 b 的先决条件,课程 b 是课程 c 的先决条件,那么课程 a 是课程 c 的间接先决条件。现在需要你根据查询数组 queries,根据 queries[i] = [u, v] 查询课程 u 是否是课程 v 的先决条件,最后返回一个 bool 类型的数组 ret,ret[i] 表示数组 queries 的第 i 次查询的结果。
解题思路
主要思路是怎么建立课程节点之间的联系。以下介绍两种方法。
方法一:Floyd传递闭包
一个直观的想法是利用提供的 prerequisites 数组现将两个课程节点连接起来,根据 F l o y d Floyd Floyd 算法传递闭包,建立课程节点之间的联系。
实现代码
class Solution {
public:vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {vector<vector<bool>> graphy(numCourses, vector<bool>(numCourses, false));for (auto pre : prerequisites) {int x = pre[0], y = pre[1];graphy[x][y] = true;}for (int k = 0; k < numCourses; ++k) { // 中间节点for (int i = 0; i < numCourses; ++i) {for (int j = 0; j < numCourses; ++j) {if (graphy[i][k] && graphy[k][j]) {graphy[i][j] = true;}}}}vector<bool> res;for (auto query : queries) {int x = query[0], y = query[1];res.push_back(graphy[x][y]);} return res;}
};
复杂度分析
时间复杂度: O ( n u m C o u r s e s 3 ) O(numCourses^3) O(numCourses3), n u m C o u r s e s numCourses numCourses 表示课程的数目,本题数据量为 1 0 2 10^2 102,因此不会超时。
空间复杂度: O ( n u m C o u r s e s 2 ) O(numCourses^2) O(numCourses2),主要是建图占用的额外空间。
方法二:拓扑排序
题目中保证没有环,可以利用拓扑排序来建立课程节点之间的联系,通过拓扑排序记录每个课程节点的直接或间接先决条件。
具体地,维护一个数组 inDegree 用来记录课程节点的入度;维护一个队列 que 存放拓扑排序的课程节点,初始化加入入度为 0 的课程节点;维护一个 edges 用来记录课程节点之间的关系;维护一个 numCourse x numCourse 的矩阵 isPre,其中 isPre[x][y] 表示课程 x 是否是课程 y 的直接或者间接先决条件。
程序执行流程,前面就是拓扑排序的常规操作,包括:
- 记录课程节点的入度;
- 建立课程节点之间的边关系;
- 将入度为
0的节点加入队列中; - 依次取出队列中入度为
0的课程节点,设当前出队的节点为x,枚举edges[x]中的课程节点y,对其进行 操作,并--inDegree[y],如果inDegree[y] = 0,则加入队列。
以上是拓扑排序的模板操作,现在来介绍一下其中的 操作。
当前出队的节点为 x,枚举 edges[x] 中的课程节点 y,于是课程节点 x 为 y 的直接先决条件,因此 isPre[x][y] = true,这时候枚举其他的课程节点 i,更新 isPre[i][y] = isPre[i][y] | isPre[i][x]。
最后,遍历查询数组的每一个查询,根据 isPre 结果即可得到每一个查询结果。
实现代码
class Solution {
public:vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {vector<int> inDegree(numCourses);queue<int> que;vector<vector<int>> edges(numCourses);vector<vector<bool>> isPre(numCourses, vector<bool>(numCourses, false));for (auto pre : prerequisites) {int x = pre[0], y = pre[1];++inDegree[y];edges[x].push_back(y);}for (int i = 0; i < numCourses; ++i) {if (inDegree[i] == 0) {que.push(i);}}while (!que.empty()) {int x = que.front();que.pop();for (auto y : edges[x]) {isPre[x][y] = true;for (int i = 0; i < numCourses; ++i) {isPre[i][y] = isPre[i][y] | isPre[i][x];}--inDegree[y];if (inDegree[y] == 0) {que.push(y);}}}vector<bool> res;for (auto query : queries) {int x = query[0], y = query[1];if (isPre[x][y]) {res.push_back(true);}else res.push_back(false);} return res;}
};/*
拓扑排序
题目中保证没有环,可以利用拓扑排序来建立课程节点之间的联系
通过拓扑排序记录每个课程节点的直接或间接先决条件
*/
复杂度分析
时间复杂度: O ( n u m C o u r s e 2 + n + m ) O(numCourse^2+n+m) O(numCourse2+n+m),其中 n u m C o u r s e s numCourses numCourses 是课程数, n n n 为数组 prerequisites 的长度, m m m 为查询数。主要是计算 isPre 矩阵的时间复杂度为 O ( n u m C O u r s e 2 ) O(numCOurse^2) O(numCOurse2),构建有向图复杂度为 O ( n u m C o u r s e s + n ) O(numCourses+n) O(numCourses+n), m m m 次查询时间复杂度为 O ( m ) O(m) O(m)。
空间复杂度: O ( n u m C o u r s e s 2 + n ) O(numCourses^2+n) O(numCourses2+n),主要是构建有向图和矩阵 isPre 的空间开销。
思考
题目中的课程节点之间的先决关系类似于一种父子关系,能否利用【并查集】的方法解决该问题呢?
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

1462. 课程表 IV
文章目录 Tag题目来源题目解读解题思路方法一:Floyd传递闭包方法二:拓扑排序 思考写在最后 Tag 【拓扑排序】【传递闭包】【并查集】【数组】 题目来源 1462. 课程表 IV 题目解读 给你一个表示课程先决条件的数组 prerequisites,prerequis…...
QTday2
完善登录框 点击登录按钮后,判断账号(admin)和密码(123456)是否一致,如果匹配失败,则弹出错误对话框,文本内容“账号密码不匹配,是否重新登录”,给定两个按钮…...

thrift的简单使用
写在前面 本文一起看下一种由facebook出品的rpc框架thrift。 源码 。 1:开发步骤 1:编写thrift idl文件 2:根据thrift idl文件生成java模板代码 3:继承模板代码的*.Iface接口给出server的具体服务实现 4:使用模板的HelloWorldSe…...
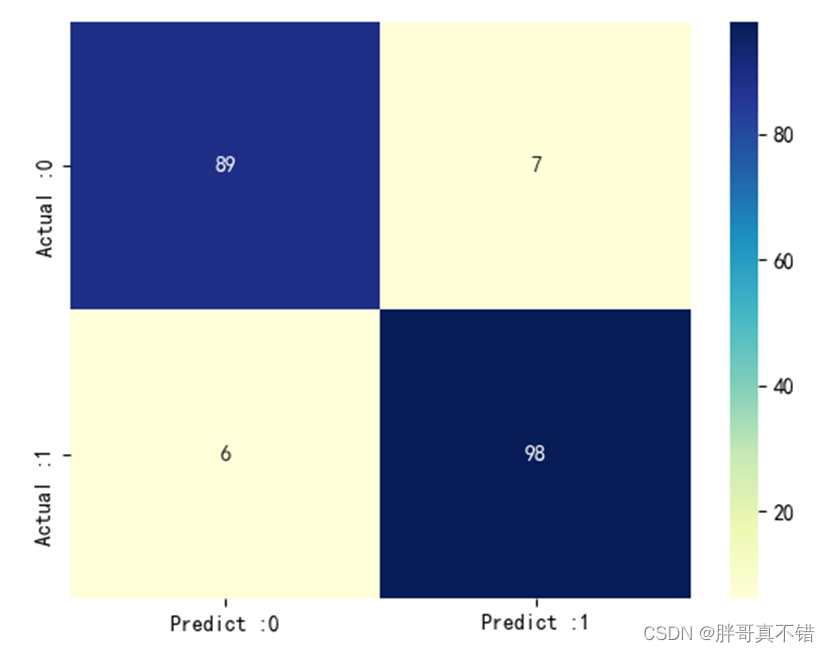
Python实现猎人猎物优化算法(HPO)优化随机森林分类模型(RandomForestClassifier算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 猎人猎物优化搜索算法(Hunter–prey optimizer, HPO)是由Naruei& Keynia于2022年提出的一种最新的…...
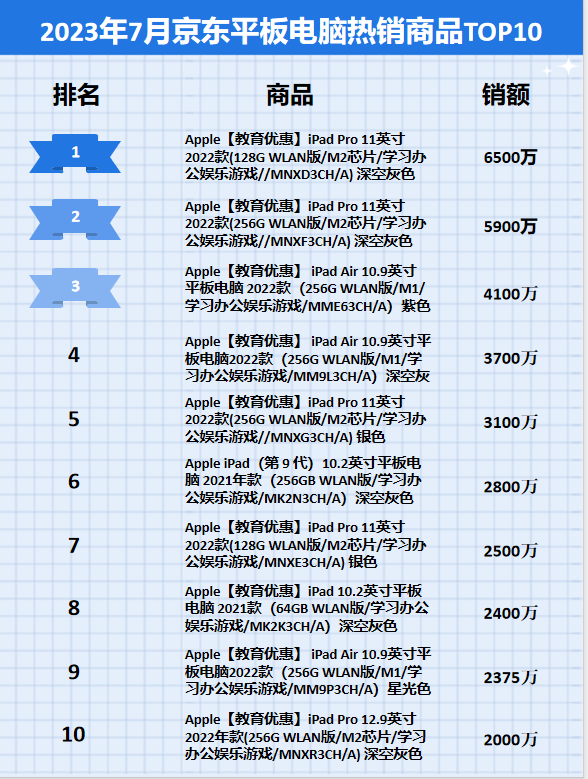
2023年7月京东平板电脑行业品牌销售排行榜(京东销售数据分析)
鲸参谋监测的京东平台7月份平板电脑市场销售数据已出炉! 根据鲸参谋电商数据分析平台的相关数据显示,今年7月份,京东平台上平板电脑的销量为68万,同比增长超过37%;销售额为22亿,同比增长约54%。从价格上看…...

HTML显示中文空格字符,emsp;一个中文字符,ensp;半个中文字符
 一个中文字符  半个中文字符 <ul><li class"li">姓  名:<input type"text" /></li><li class"li">手 机 号:<input type"…...

Python基础指令(上)
Python基础指令上 常量和表达式变量和类型1. 什么是变量2. 变量的语法2.1 定义变量2.2 使用变量 3. 变量的类型4. 为什么要有这么多类型5. 动态类型特性 注释输入输出1. 程序与用户的交互2. 通过控制台输出3. 通过控制台输入 运算符1. 算术运算符2. 关系运算符3. 逻辑运算符4. …...

Python之FastAPI返回音视频流
Python之FastAPI返回音视频流 今天想要记录一下困扰我几天的一个问题,关于FastAPI返回音视频流。首先FastAPI挂载静态资源其实超级简单,但是对于音视频流,如果你想要有播放进度可以拖动,需要单独处理。 有以下几点想跟大家分享&a…...
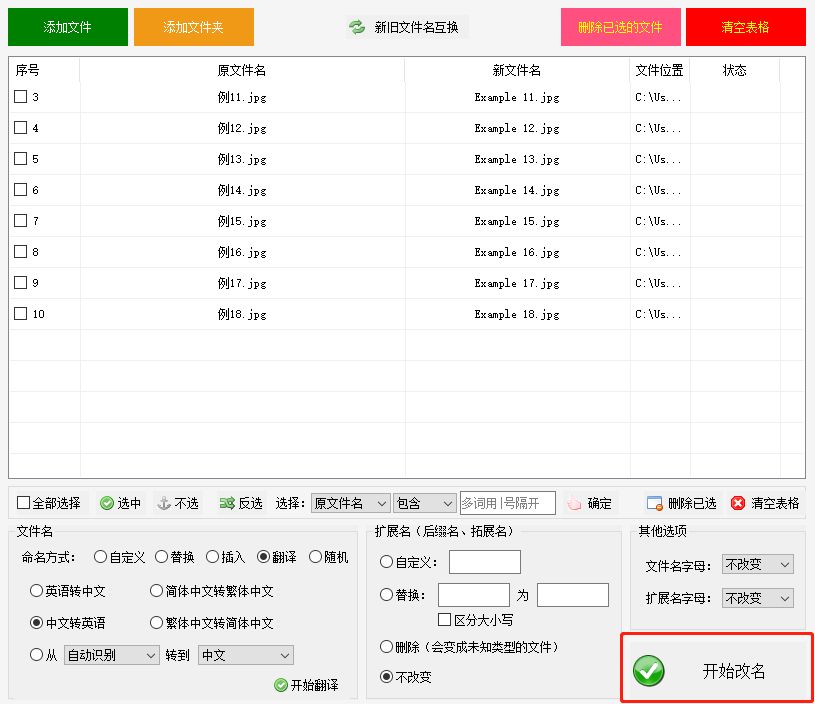
文件名批量重命名与翻译的实用指南
在日常办公中,我们经常遇到需要批量修改文件名并进行翻译的情况。手动一个一个修改文件名既费时又繁琐,而且还可能出现错误。今天,我们将介绍一种高效的方法,利用文件管理工具“固乔文件管家”,能够快速批量修改文件名…...

上海长宁来福士P2.5直径4米无边圆形屏圆饼屏圆面屏圆盘屏平面圆屏异形创意LED显示屏案例
长宁来福士广场是一个大型广场,坐落于上海中山公园商圈的核心区域,占地逾6万平方米,其中地上总建筑面积近24万平方米,总投资额约为96亿人民币。 LED圆形屏是根据现场和客户要求定制的一款异形创意LED显示屏,进行文字、…...
Linux 企业级夜莺监控分析工具远程访问
文章目录 前言1. Linux 部署Nightingale2. 本地访问测试3. Linux 安装cpolar4. 配置Nightingale公网访问地址5. 公网远程访问Nightingale管理界面6. 固定Nightingale公网地址 前言 夜莺监控是一款开源云原生观测分析工具,采用 All-in-One 的设计理念,集…...
react使用内联css样式的注意点
react使用内联css样式: 就是直接在元素标签的style属性中写css样式,但是这里有三个注意点: 1. style等号后面必须接双大括号也就是 style{{ xx: xx }} 这样 2. css的属性必须写成驼峰型,不能有中横线,比如marginRight, 而不能说margin-righ…...

优先队列PriorityQueue源码解析
基本信息 实现了队列接口:Queue --> AbstractQueue --> PriorityQueue public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {public abstract class AbstractQueue<E> extends AbstractCollection…...

前端开发中常见的跨域问题及解决方案
引言 在前端开发中,跨域问题是一个非常常见的问题。本文将详细介绍什么是跨域,常见的跨域场景,以及各种常用的跨域解决方案。 什么是跨域 跨域是指一个网页或者Web应用在浏览器中发起对另一个域名下资源的请求。由于浏览器的同源策略限制&…...
(超详解)堆排序+(图解)
目录: 1:如何建堆(两种方法) 2:两种方法建堆的时间复杂度分析与计算 3:不同类型的排序方式我们应该如何建堆 文章正式开始: 1:如何建堆 在实现堆排序之前我们必须得建堆,才能够实现堆排序 首先在讲解如何建堆之前让我们先来回顾一…...

Hadoop的YARN高可用
一、YARN简介 Hadoop2.0即第二代Hadoop,由分布式存储系统HDFS、并行计算框架MapReduce和分布式资源管理系统YARN三个系统组成,其中YARN是一个资源管理系统,负责集群资源管理和调度,MapReduce则是运行在YARN上的离线处理框架。 Y…...

C++内存检查
内存泄漏是程序中常见,也是最令人痛苦的一种bug。好在有一些检查工具可以帮助我们,这里介绍一个google 提供的简单直接的工具 Address-Sanitizer (ASAN)。 预备条件 ASAN 原来是LLVM 中的特性,后来GCC 4.8中也开始支持。也就是说࿰…...

防火墙概述及实战
目录 前言 一、概述 (一)、防火墙分类 (二)、防火墙性能 (三)、iptables (四)、iptables中表的概念 二、iptables规则匹配条件分类 (一)、基本匹配条…...
nginx代理故障总结
一、故障现象 今天公司的某个系统文件下载功能失败,报错network error,其他功能正常。 二、故障定位 首先我们检查了公司的网络情况,包括网络路由、防火墙策略、终端安全产品等,均未发现异常。 尝试访问http://X.X.X.X:7002端口&…...
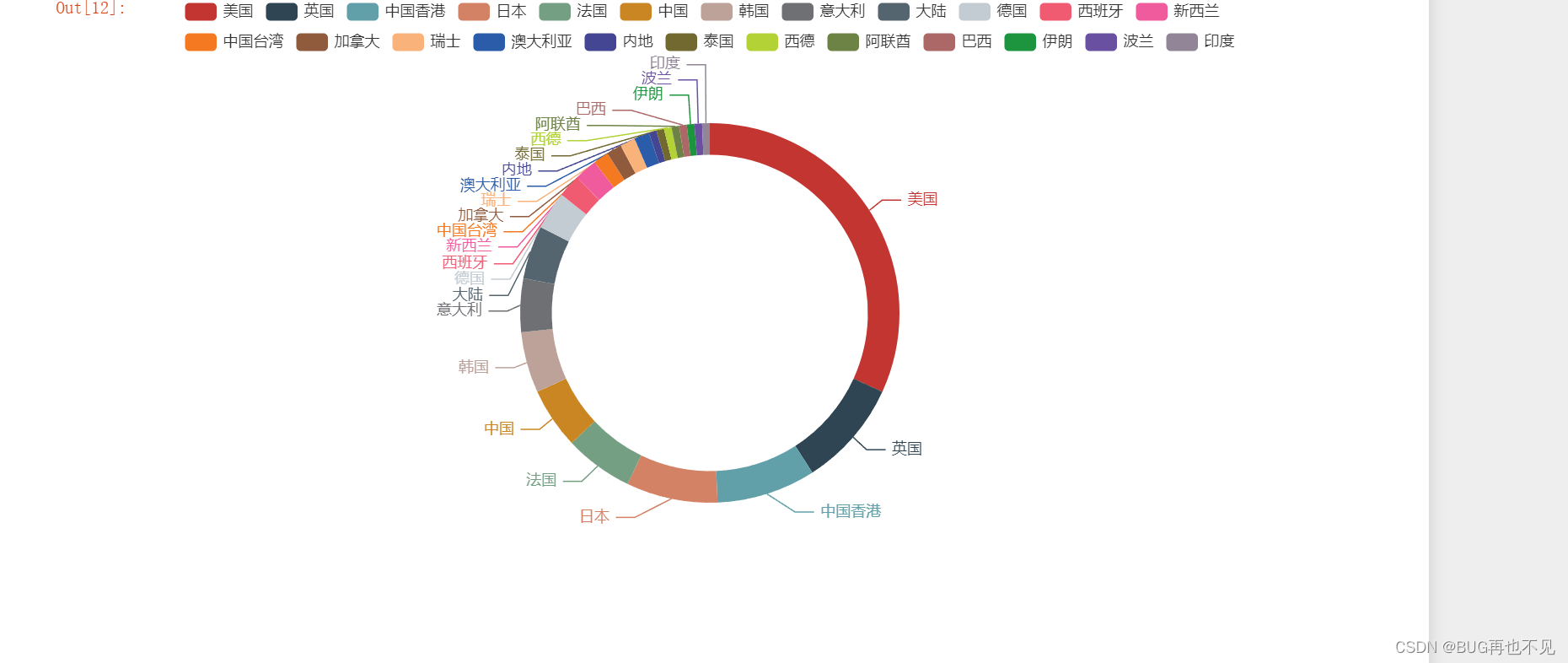
python爬虫爬取电影数据并做可视化
思路: 1、发送请求,解析html里面的数据 2、保存到csv文件 3、数据处理 4、数据可视化 需要用到的库: import requests,csv #请求库和保存库 import pandas as pd #读取csv文件以及操作数据 from lxml import etree #解析html库 from …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
