深度学习-偏导数复习
文章目录
- 前言
- 1.偏导数
- 2.偏导数概念
- 1.对x的偏导数
- 2.对y的偏导数
- 3.多元函数偏导数
- 4.如何计算偏导数
- 1.二元函数的偏导数
- 2.复杂函数的偏导数
- 3.分段函数
- 1.分界点的偏导数
- 5.偏导数与连续之间的关系
- 6.偏导数的几何意义
- 7.高阶偏导数
- 1.定义
- 2.高阶偏导数例题(二阶偏导数)
- 3.全微分
- 1.偏增量定义
- 2.全增量定义
- 3计算方式
- 4.多元函数微分学的几何应用
- 1.定义
- 2.例题1
- 5.方向导数
- 1.方向导数定义
- 2.方向导数的计算
- 3. 方向导数和偏导数的关系
- 4.方向导数计算
- 1.例题1
- 1.例题2
- 5.三元函数的方向导数
- 1.定义
- 2.例题1
- 3.例题2
- 6.梯度
- 1.定义-梯度就是沿着这个方向,方向导数能达到最大值
- 2.方向导数和梯度的关系
- 1.向量内积
- 2.向量数量积
- 3.梯度与方向导数
- 4.梯度总结
- 5.梯度的角度
- 6.梯度的计算-1
- 7.梯度的计算-2
- 8.梯度的计算-3
- 7 梯度下降
前言
为了更好的理解梯度下降,重新看了一下梯度下降的高数课长,现在根据学习内容,把课件贴图,防止哪一天自己记不起来。
下面的内容是通过B站视频整理而来。
高数学习


1.偏导数
偏导数是一个整体,不能拆开


2.偏导数概念
1.对x的偏导数

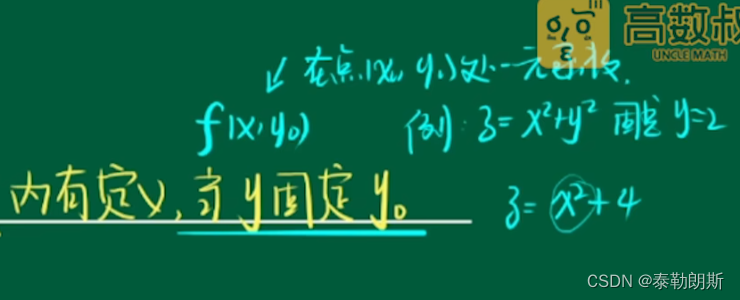
2.对y的偏导数


3.多元函数偏导数

4.如何计算偏导数

1.二元函数的偏导数

2.复杂函数的偏导数


3.分段函数
1.分界点的偏导数
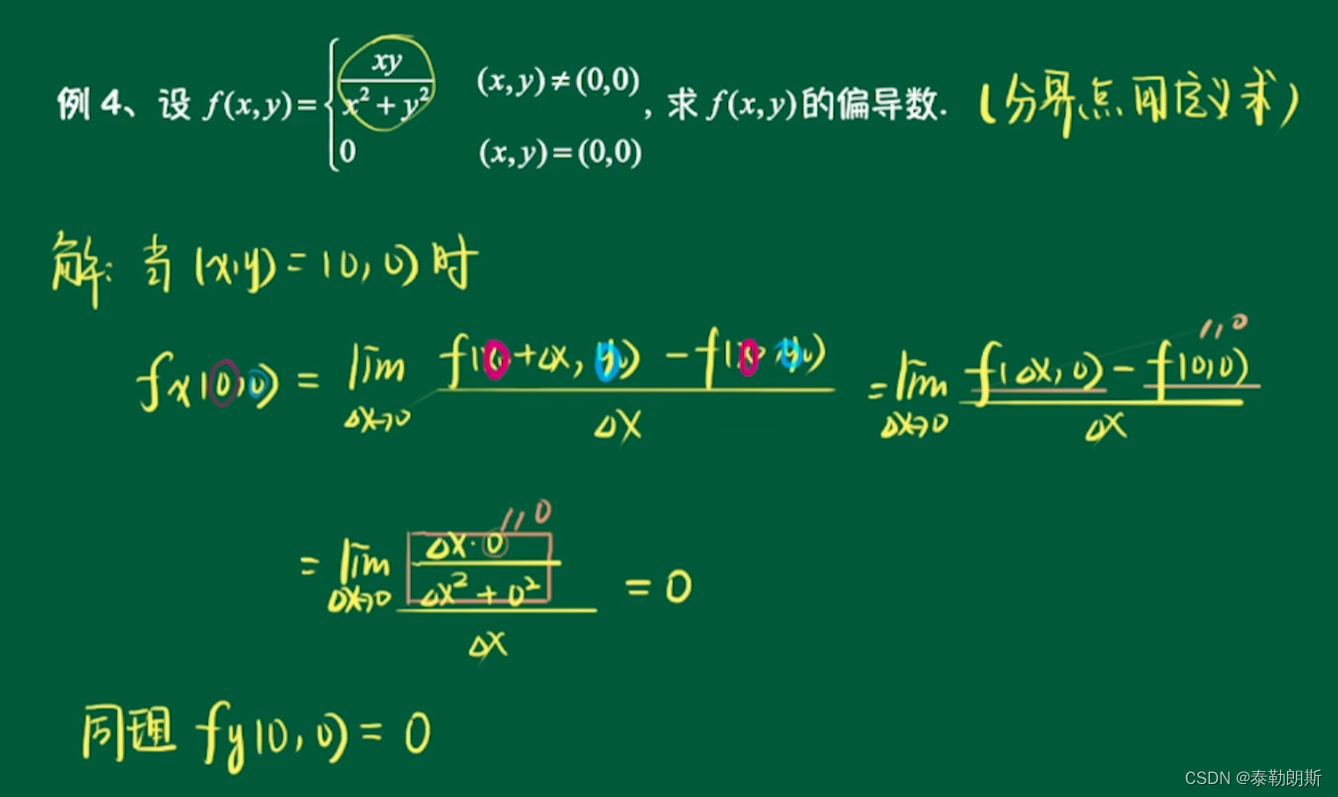
因为x,y是对称函数,所以它们俩的偏导数是相同的。
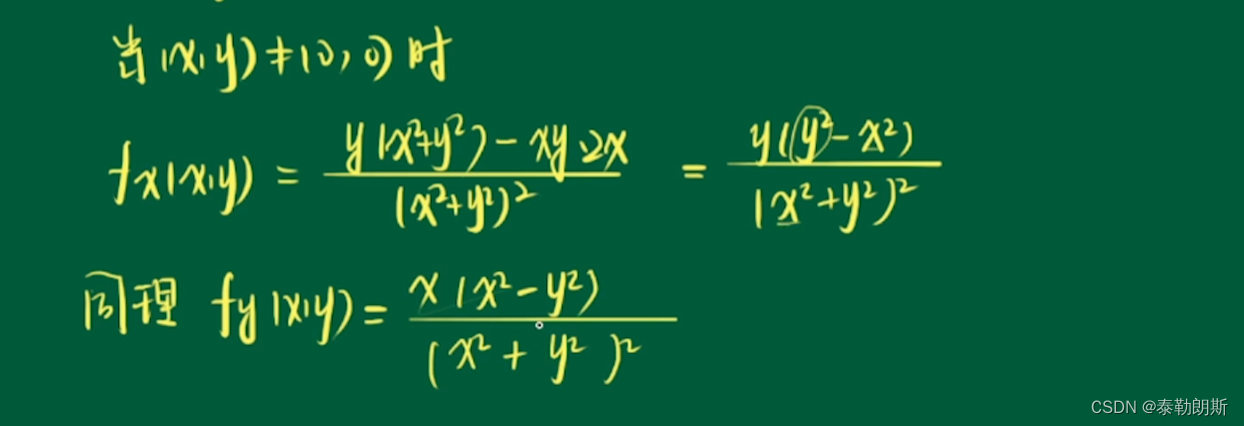
。
5.偏导数与连续之间的关系
沿着不同方向趋近于0,那么y=kx
二元函数,偏导数存在,不能证明二元函数连续

6.偏导数的几何意义
偏导数是正交的

7.高阶偏导数
1.定义

2.高阶偏导数例题(二阶偏导数)
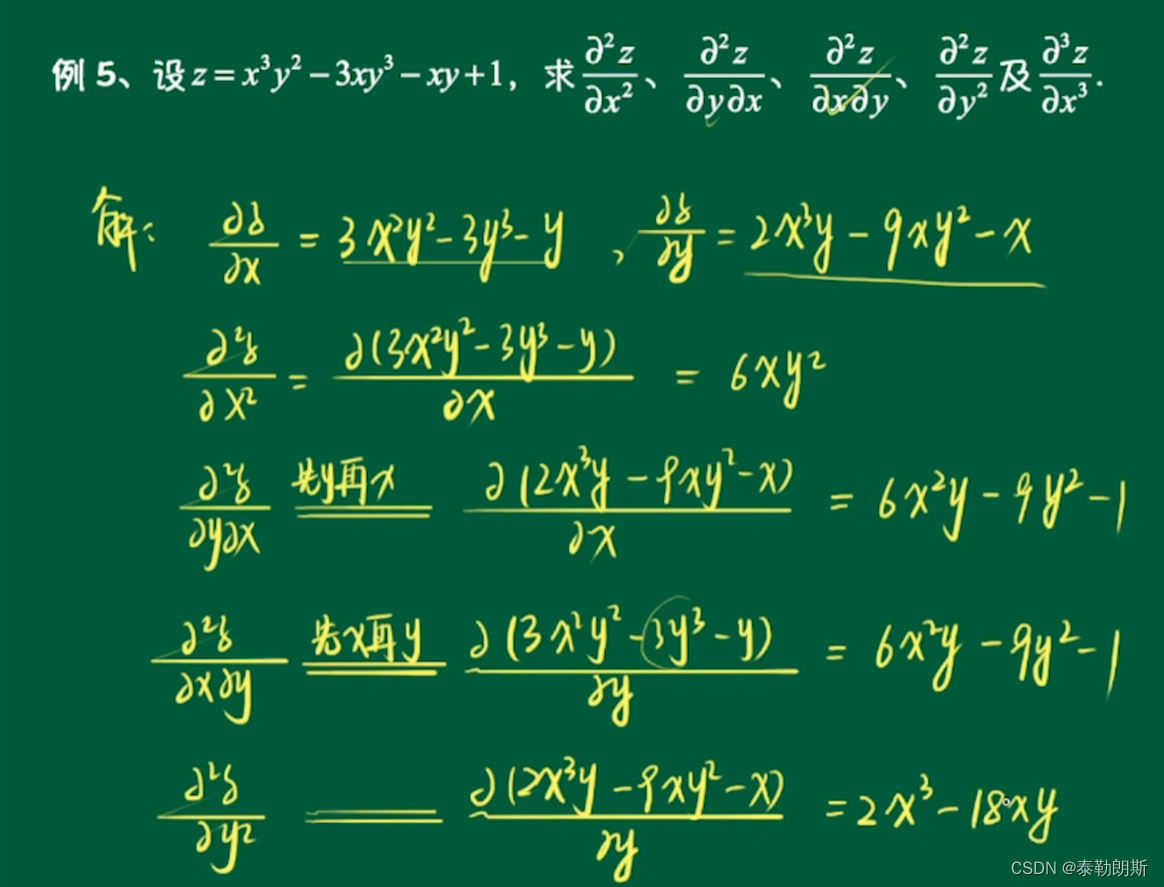
3.全微分
A,和B是和x,y有关的量

1.偏增量定义

2.全增量定义
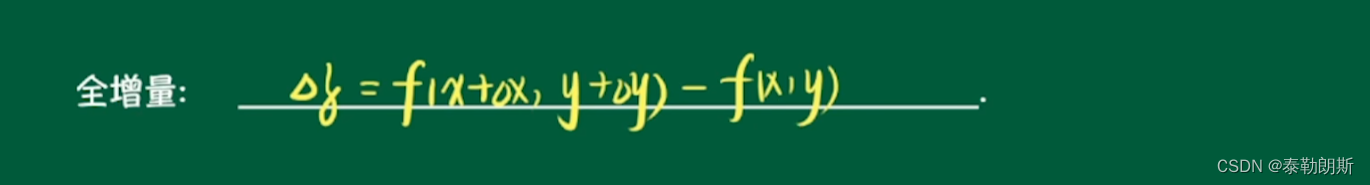
3计算方式
4.多元函数微分学的几何应用
1.定义


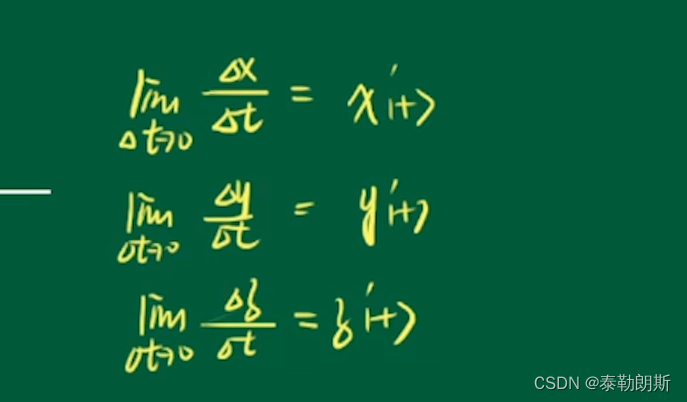
最后求出切线的方程
<img src=https://img-blog.csdnimg.cn/603f8d6256c54b3abb60d39f710506c4.png" width=800>
曲线的切向量
法平面

2.例题1

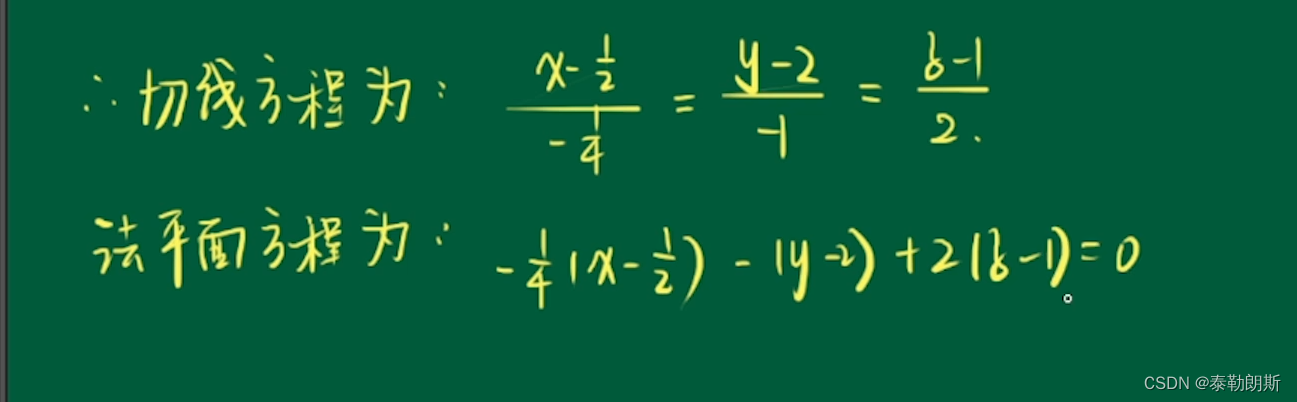
5.方向导数
1.方向导数定义


说明平面是连续的
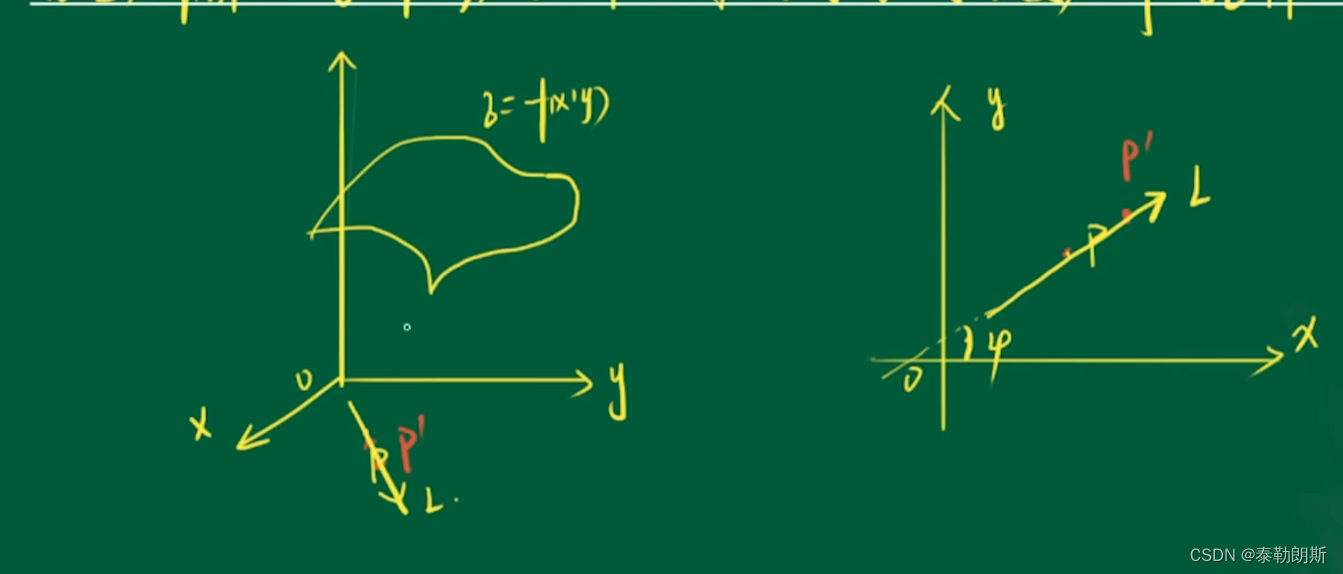
2.方向导数的计算
导数就是斜率,方向导数就是某个点平面的斜率值
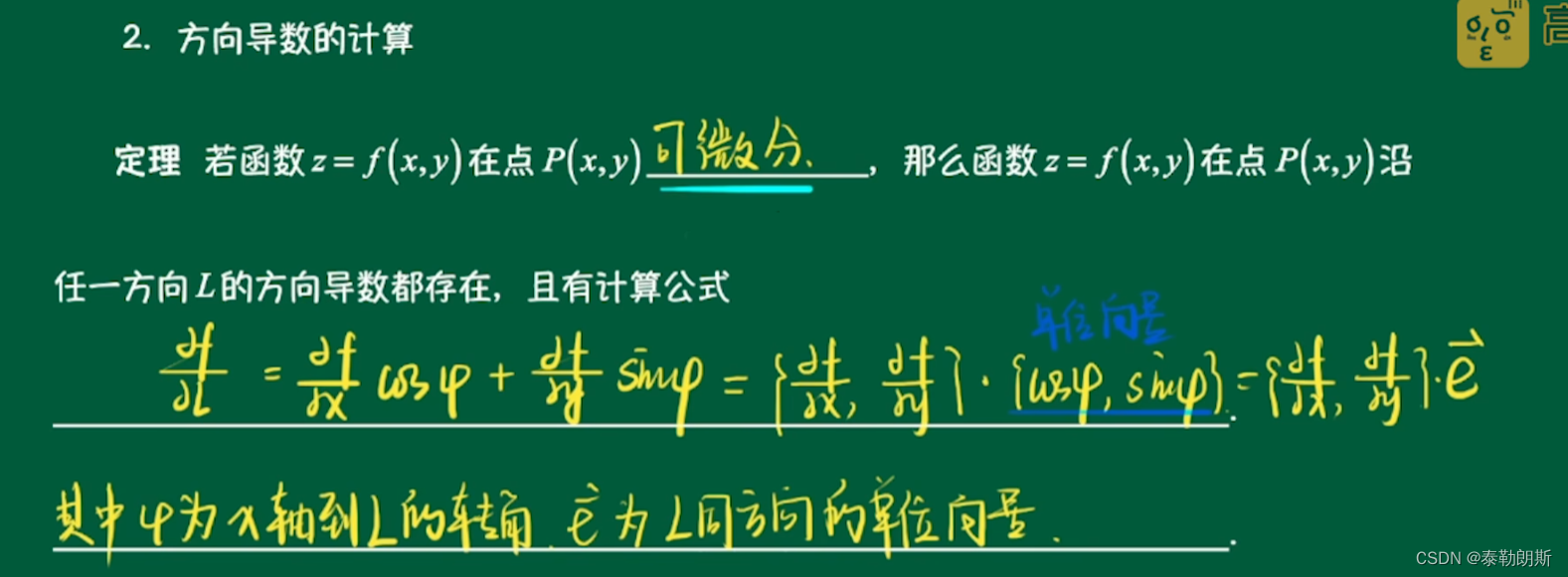
方向导数是关于角度的函数,因为偏导数已经确定了
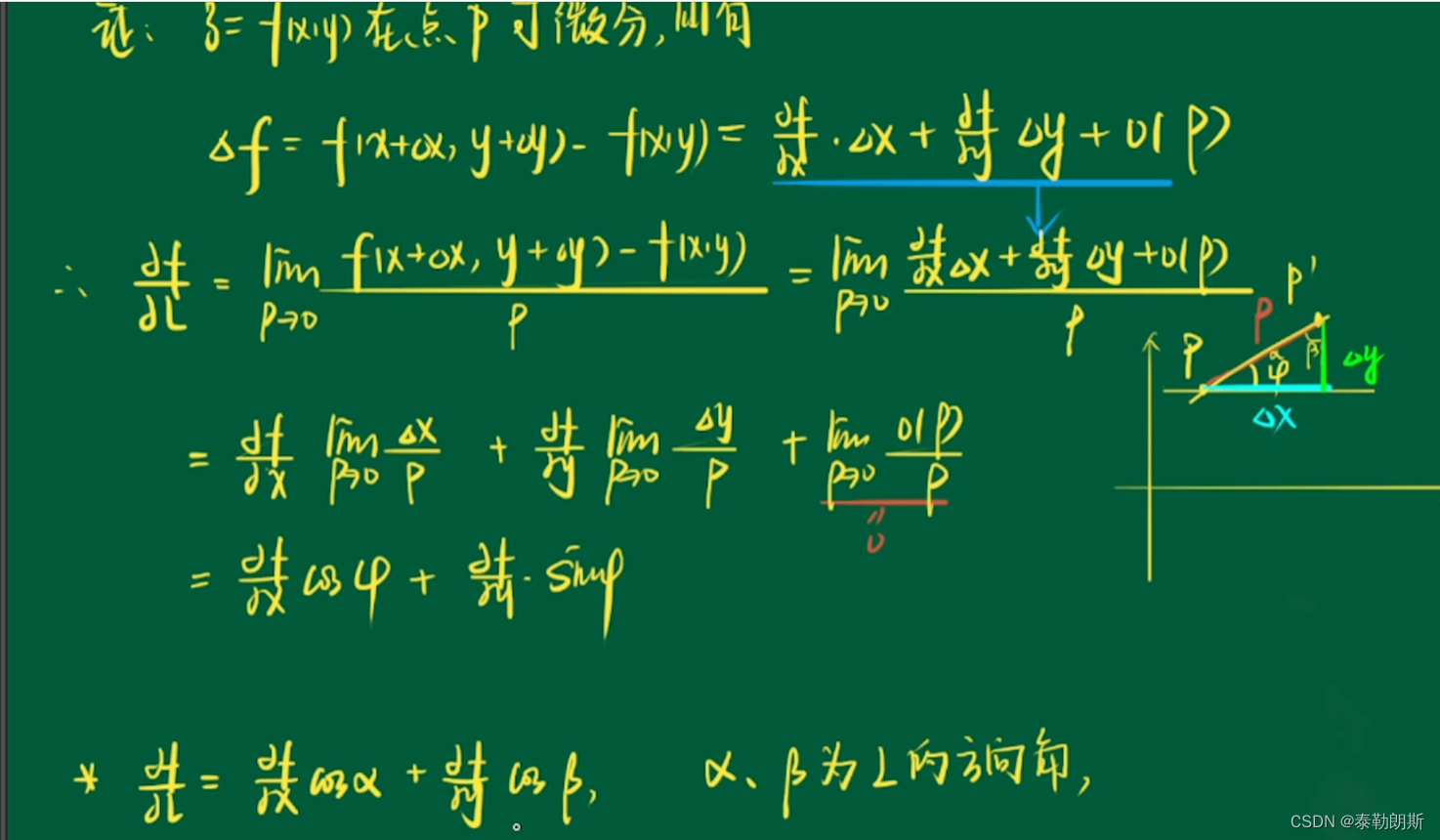
3. 方向导数和偏导数的关系
方向导数存在,偏导数就存在,反之则不一定
方向导数是偏导数的推广

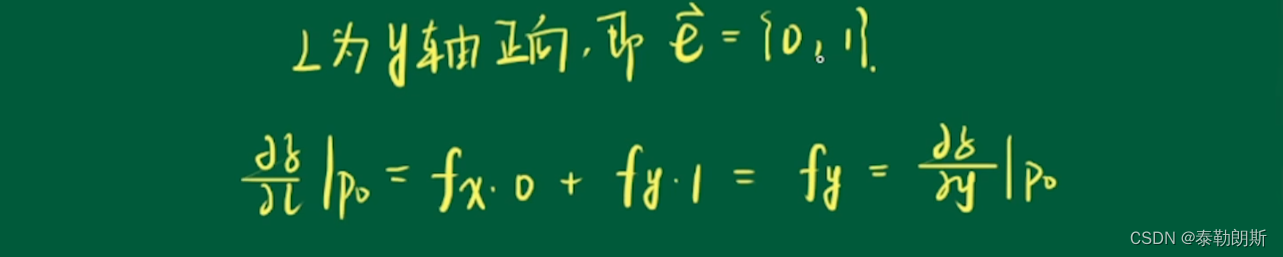
4.方向导数计算
1.例题1

1.例题2
5.三元函数的方向导数
1.定义

2.例题1

3.例题2

6.梯度
1.定义-梯度就是沿着这个方向,方向导数能达到最大值
单位向量,是指模等于1的向量

单位向量有无数个
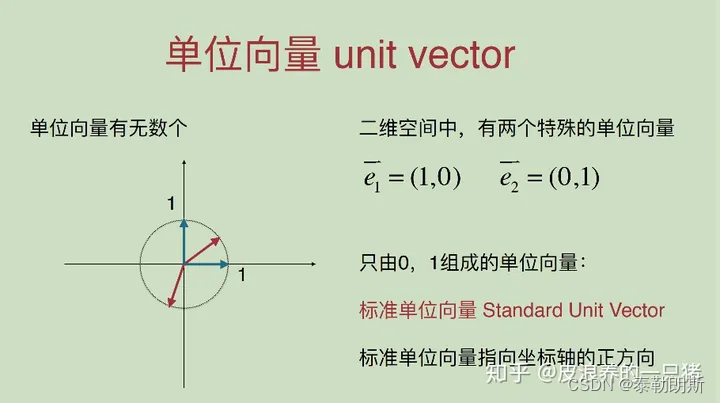
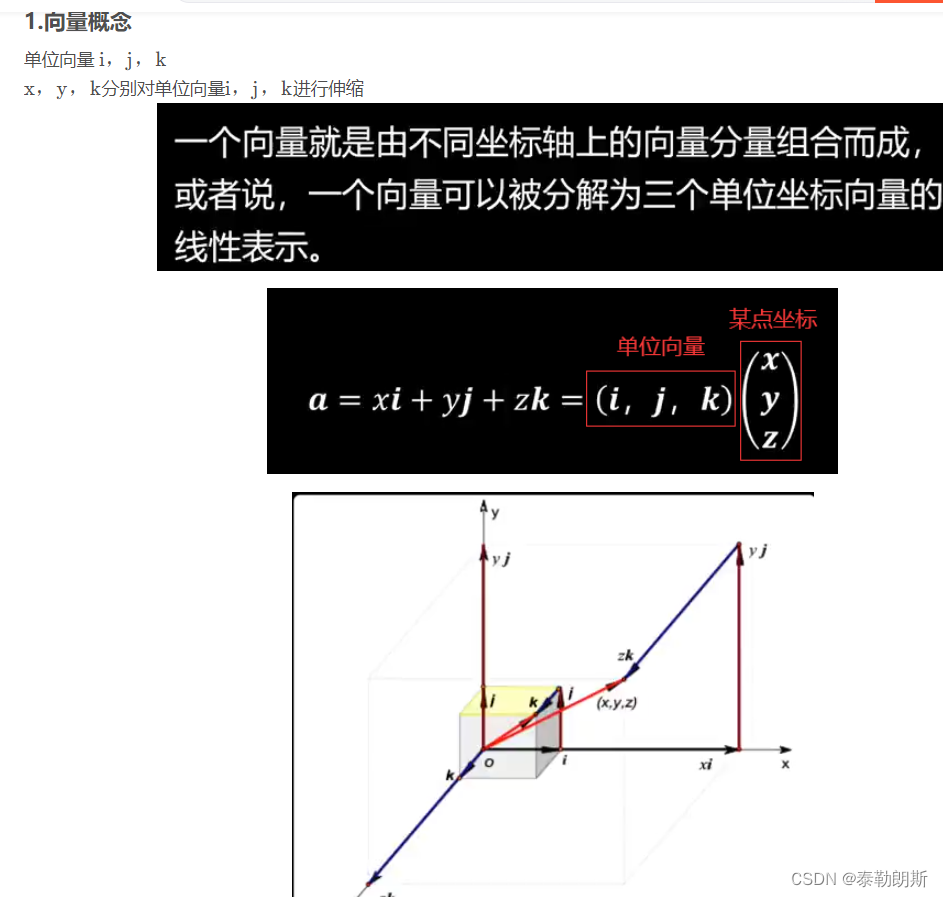
梯度就是沿着这个方向,方向导数能达到最大值

2.方向导数和梯度的关系
1.向量内积

2.向量数量积

3.梯度与方向导数
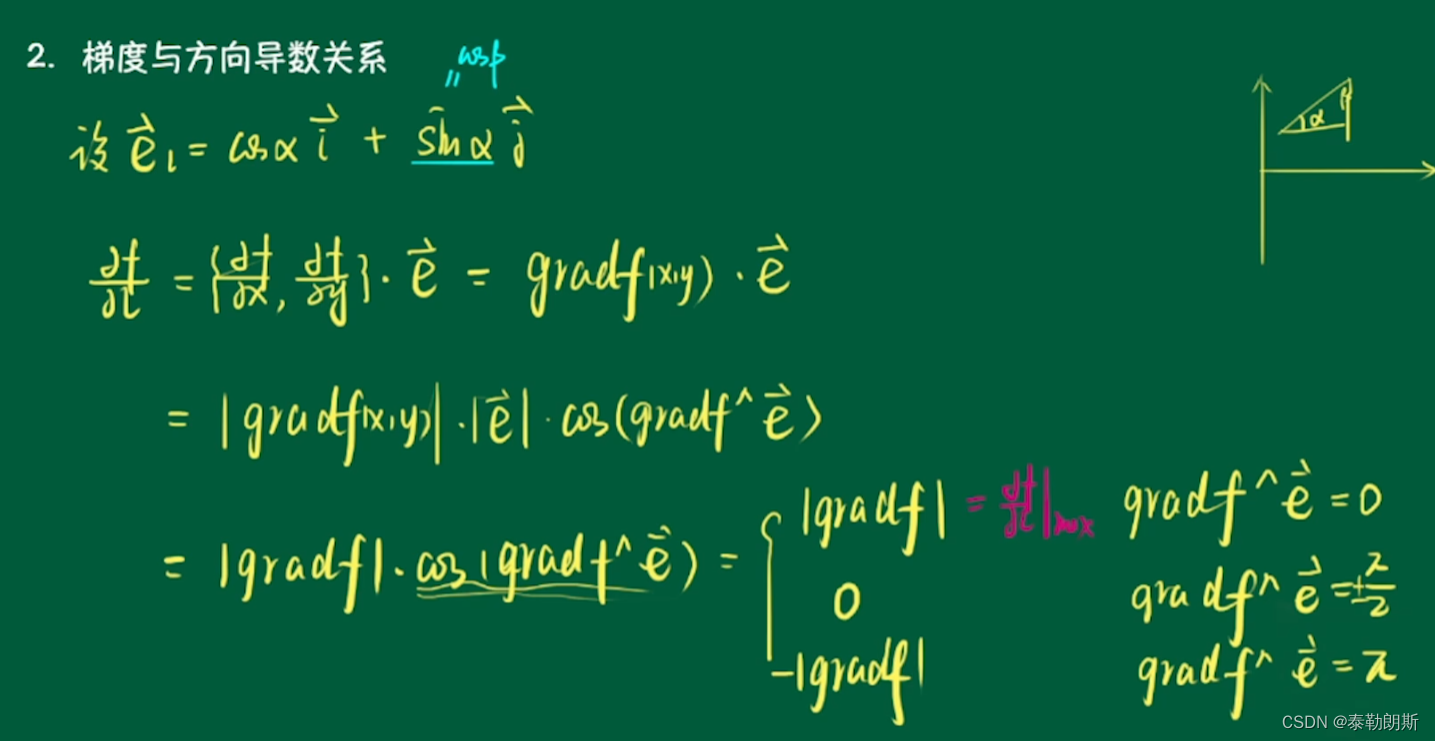
4.梯度总结

5.梯度的角度

6.梯度的计算-1
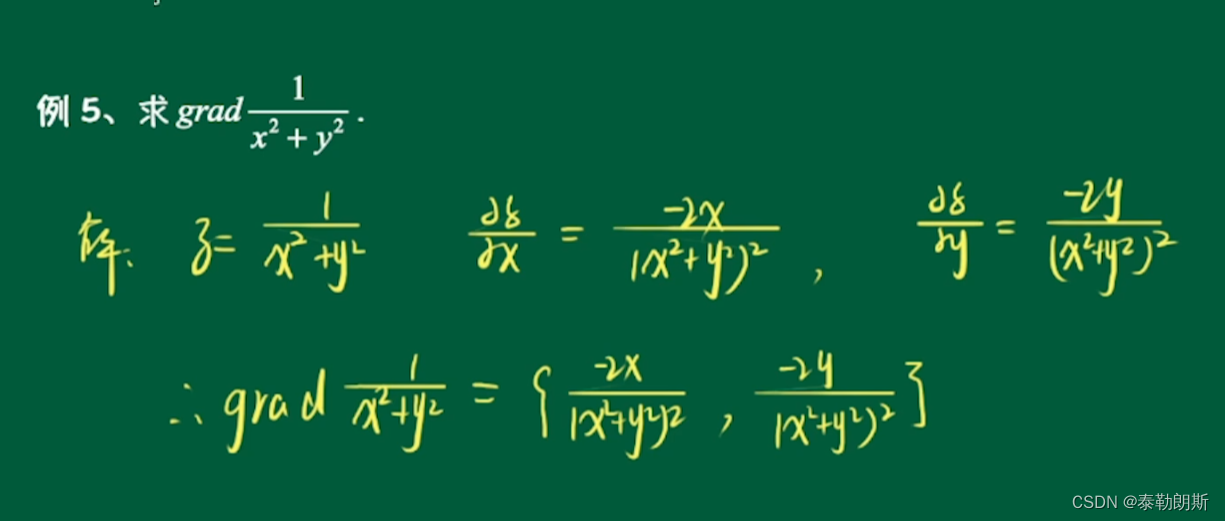
7.梯度的计算-2
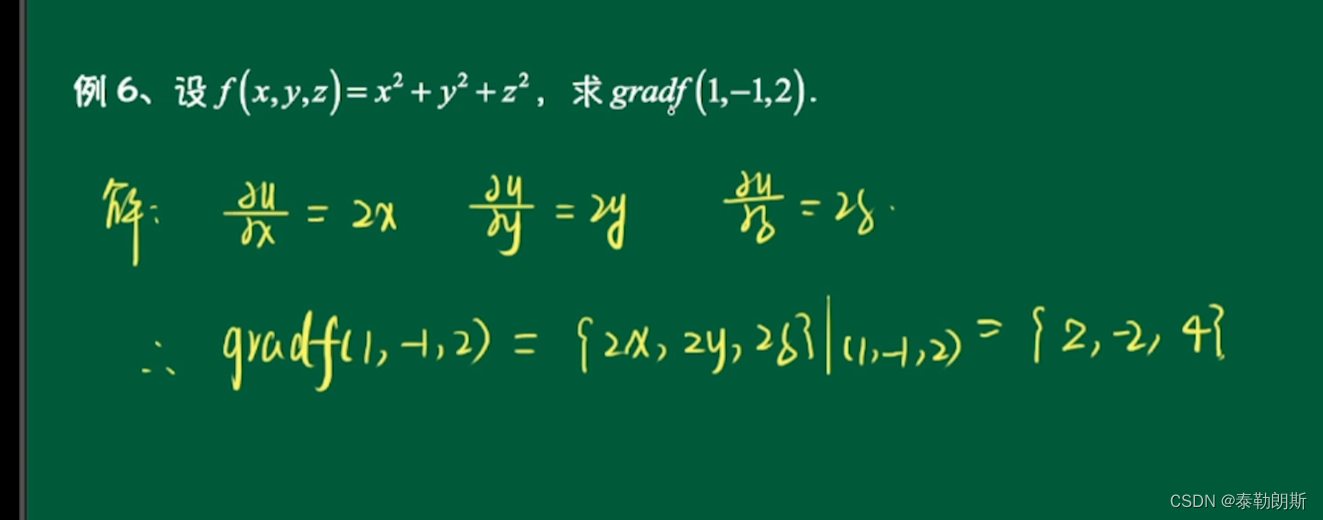
8.梯度的计算-3
7 梯度下降

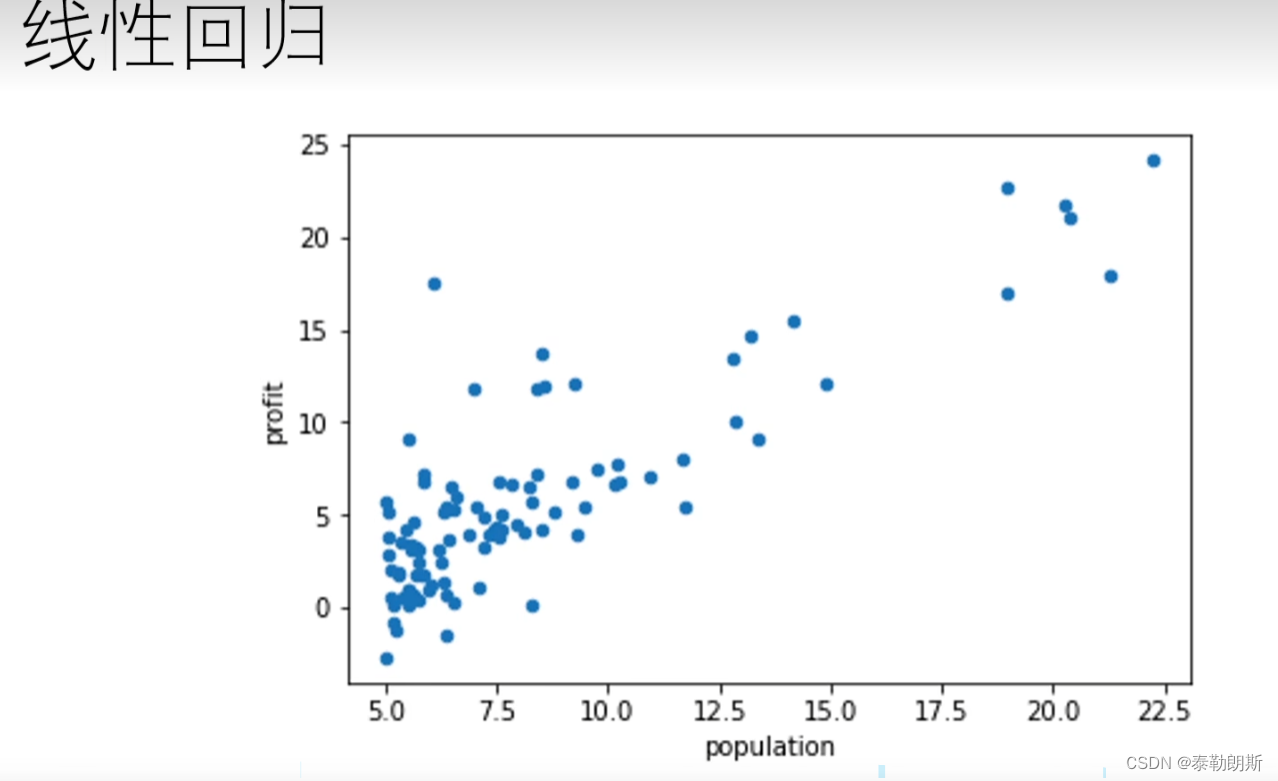

、

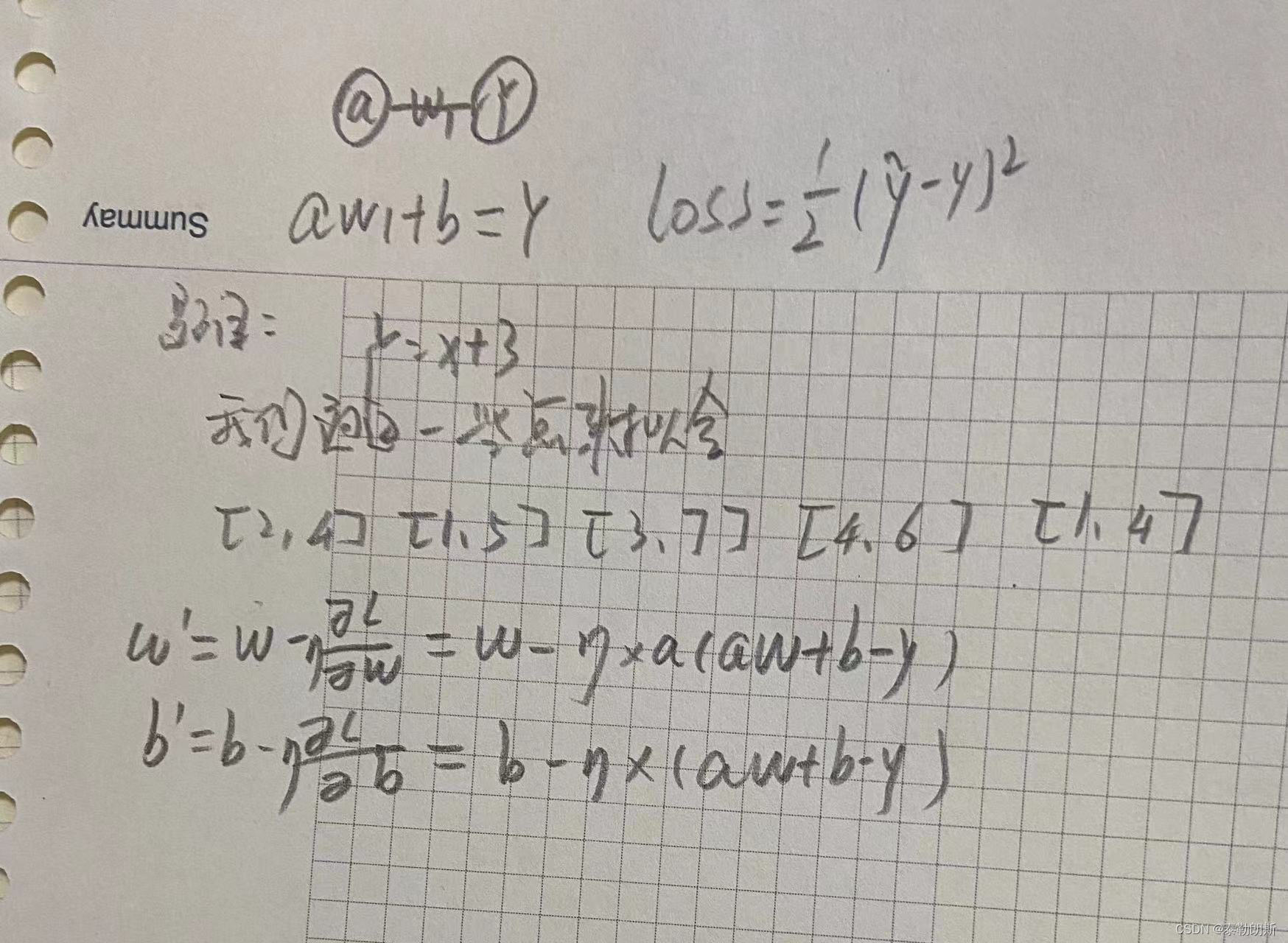
import osw=2
b=2n=0.1array=[[2,4],[1,5],[3,7],[4,6],[1,4],[2,5],[3,6]]for j in range(5):for i in range(len(array)):a=array[i][0]y=array[i][1]w1=w-n*a*(a*w+b-y)b1=b-n*(a*w+b-y)w=w1b=b1print(w,b)
相关文章:

深度学习-偏导数复习
文章目录 前言1.偏导数2.偏导数概念1.对x的偏导数2.对y的偏导数3.多元函数偏导数4.如何计算偏导数1.二元函数的偏导数2.复杂函数的偏导数3.分段函数1.分界点的偏导数 5.偏导数与连续之间的关系6.偏导数的几何意义7.高阶偏导数1.定义2.高阶偏导数例题(二阶偏导数&…...

linux之jq命令
jq命令用于linux命令行对json进行处理 参数 option -r:去掉字符串的引号"例子 tt.json文件如下: [{"metric": "httpcode","tags": {"cluster": "tt","domain": "www.baidu.…...
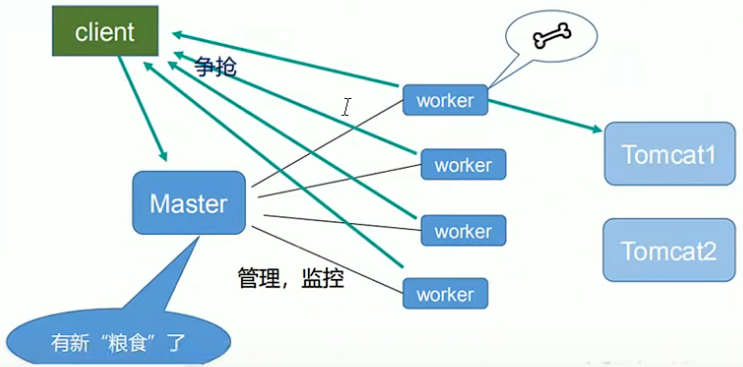
nginx知识点详解:反向代理+负载均衡+动静分离+高可用集群
一、nginx基本概念 1. nginx是什么,做什么事情? Nginx是一个高性能的HTTP和反向代理服务器,特点是占有内存少,并发能力强。Nginx转为性能优化而开发,能经受高负载考验。支持热部署,启动容易,运…...

powerDesigner 的基本使用
打开powerDesigner 新建 PDM(物理数据模型) 添加表字段 双击表,设置ID自增 选择导出数据库表SQL 导出成功 使用三方工具连接数据库,然后运行对应SQL文件即可 导入SQL文件数据到powerDesigner...

Java下打印一个等腰三角型
想达到这个结果,通常的做法是通过拼结两个三角型达到,但是实际上还有最右边的第三个三角型没有处理,这个拼结的方法总让人看起来有一点不完美的感觉,于是我自创了一个思路,一气合成,代码如下(本…...
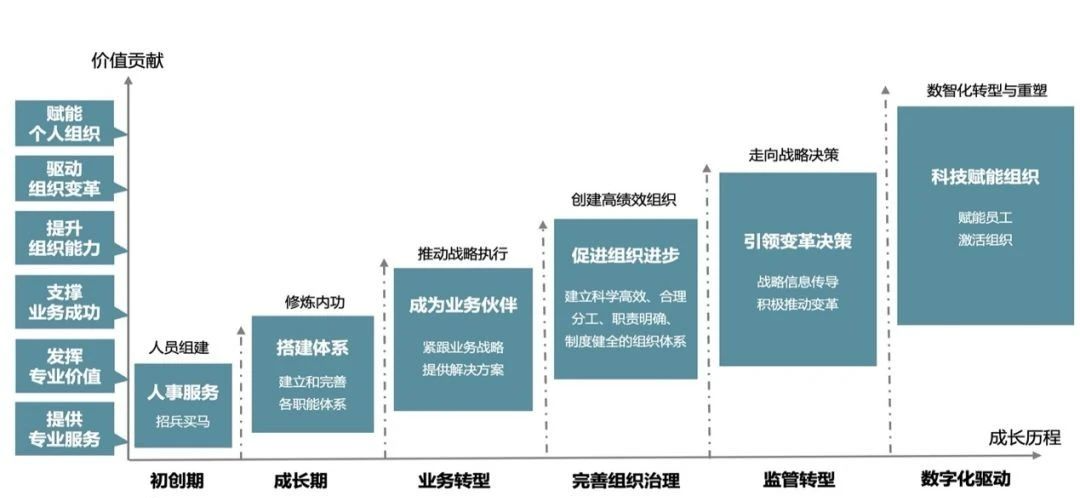
HR的职业规划
CHRO可以说是HR职业发展的天花板了。CHRO对一个企业来说至关重要,是CEO的左膀右臂。那从CEO的角度来看CHRO,应该具备什么样的素质和能力,又能为公司带来什么样的价值呢? 在公司的不同发展阶段,HR部门有着不同的战略和…...
avi怎么转换成视频?
avi怎么转换成视频?在我们日常使用的视频格式中,AVI是一种常见且经常被使用的音频视频交叉格式之一。它的优点之一是占用的存储空间相对较小,但也明显存在着画质损失的缺点。虽然AVI格式的视频在某种程度上也很常见,但与最常见的M…...

爬虫数据存储:技术、策略与实践(一)
文章目录 🍋引言🍋xlrd库和xlwt库🍋创建Excel文件🍋通过Python代码向Excel写入数据🍋案例实战 🍋引言 本节主要介绍一下在使用网络爬虫技术的时候,如何将数据存储到Excel中去 🍋xl…...

【音视频】ffplay解析-音视频同步
音视频同步 主要解析:以音频为基准,让视频合成音频 思路 视频慢了则丢掉部分视频帧(视觉->画⾯跳帧) 视频快了则继续渲染上⼀帧 具体实现 一个国际标准:音频帧-视频帧时间戳的差值在-100ms~25ms内流畅 1.差值音频…...

虚拟列表 - Vue3实现一个可动态改变高度的虚拟滚动列表
虚拟列表 - Vue3实现一个可动态改变高度的虚拟滚动列表 前言 在开发中经常遇到大量的渲染列表数据问题,往往我们就只是简单地遍历渲染,没有过多地去关注是否会存在性能问题,这导致如果数据量较大的时候,比如上万条数据ÿ…...
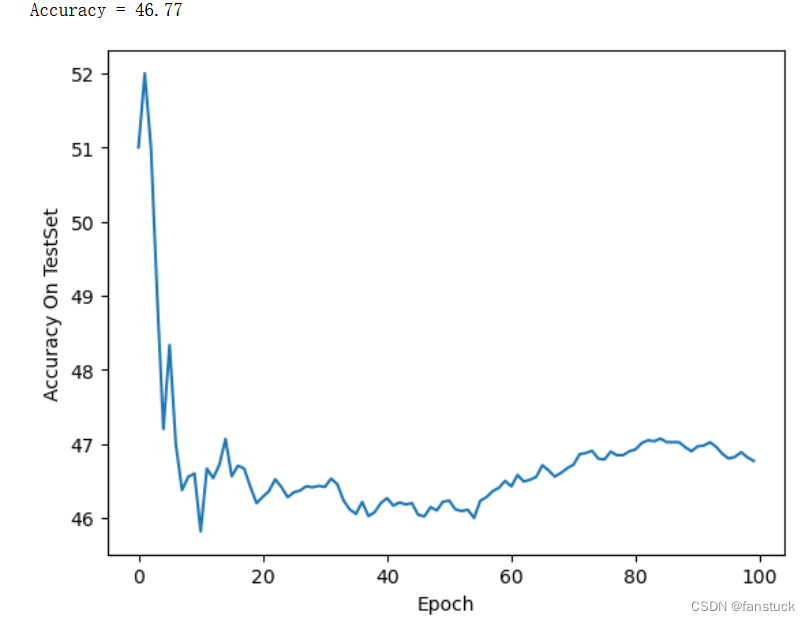
PyTorch实战:实现Cifar10彩色图片分类
目录 前言 一、Cifar10数据集 class torch.utils.data.Dataset torch.utils.data.DataLoader 二、定义神经网络 普通神经网络: 定义损失函数和优化器 训练网络-Net CPU训练 模型准确率 编辑 GPU训练 训练网络-LeNet 模型准确率 点关注,防走丢&#x…...
Vue模板语法(下)
一.事件处理器 什么是事件处理器 建立一个HTML编写事件处理器 测试结果 二.表单的综合案例 什么是表单综合案例 建立一个HTML来编写表单案例 测试结果 三.局部组件 什么是组件通信 自定义组件 测试结果 组件通信-父传子 测试结果 组件通信-子传父 测试结果 一.事件…...

uniapp掉完接口后刷新当前页面方法
uniapp掉完接口后刷新当前页面方法 掉完接口,里面加下面这个方法uni.redirectTo({}) setTimeout(() > {uni.redirectTo({// 当前页面路由url: /pages/property/mutualrotation/mutualrotation);}, 500)实例 mutualRotationSubmit() {let self this;uni.showMod…...

linux安装redis超级详细教程
redis源码安装 安装gcc redis是C语言编写的,所以我们需要先在Linux上安装和升级,C语言的编译环境。 #安装gcc yum install -y gcc-c autoconf automake#centos7 默认的 gcc 默认是4.8.5,版本小于 5.3 无法编译,需要先安装gcc新版才能编译 gcc -v#升级…...

2023-09-20 事业-代号z-个人品牌-数据库内核专家-分析
摘要: 在个人品牌层面, 必然脱离不开技术本身, 而身为数据库内核专家, 让别人尽快感知到我的专家身份至关重要. 本文从过去的经历中分析和思考, 如何尽快以技术专家的身份被感知. 过去所见过的高管的技术特点: 不在一线处理具体的事情技术理论深厚, 广度非常厉害, 知道很多相…...

UVA-1343 旋转游戏 题解答案代码 算法竞赛入门经典第二版
GitHub - jzplp/aoapc-UVA-Answer: 算法竞赛入门经典 例题和习题答案 刘汝佳 第二版 题目其实不难,但是耗费了我较多时间。 这种题关键就是在于找到约束条件,我在DFS的基础上,试了很多种策略: 1. 对3种数字,每种数字…...
【运维篇】二、配置文件与多环境控制
文章目录 1、临时属性2、IDEA中的临时属性3、配置文件4级分类4、关于四级分类的思考5、自定义配置文件6、多环境开发(yaml版)7、配置文件按环境分类8、include与group再细粒度9、一点思考10、多环境开发兼容问题 1、临时属性 jar包或者镜像已经打完了&a…...

【WFA】 VHT-5.2.27 Pre-requisite throughput lower than expected
先看仪表log,可以看到log中只有0.00346666666667Mbps,说明了速率很低 ~~~~~ Storing throughput ~~~~~ Mon, 11 Sep 2023 13:13:06 INFO strmTimeStampList2 count 1 Mon, 11 Sep 2023 13:13:06 INFO Storing $X1 = 0.00346666666667 [Mbps] Mon, 11 Sep 2023 13:13:…...

Pytorch史上最全torch全版本离线文件下载地址大全(9月最新)
以下为pytorch官网的全版本torch文件离线下载地址 torch全版本whl文件离线下载大全https://download.pytorch.org/whl/torch/其中的文件版本信息如下所示(部分版本信息,根据需要仔细寻找进行下载):...

CentOS服务器利用docker搭建中间件命令集合
一、挂载服务器磁盘 #挂盘语句 fdisk /dev/vdb 在分别输入n、p、1、2048、1048575999、w mkfs.ext4 /dev/vdb mkdir /data echo /dev/vdb /data ext4 defaults 0 0 >> /etc/fstab mount -a df -hfirewall-cmd --zonepublic --add-port8002/tcp --permanent firewall-c…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
