007 数据结构_堆——“C”
前言
本文将会向您介绍关于堆Heap的实现
具体步骤
tips:本文具体步骤的顺序并不是源代码的顺序
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
初始化
void HeapCreate(Heap* hp, HPDataType* a, int n)
{hp->_a = NULL;hp->_size = 0;hp->_capacity = 0;
}
扩容
解析:扩容的逻辑很简单,没什么可讲的,要注意的点有这里不要使用malloc,当再次需要扩容的时候,malloc函数只会分配新的内存空间,不会复制原有内存空间的内容,realloc函数会在分配新的内存空间时,将原有内存内容复制到新的内存空间中,并释放原有空间内容//扩容
void CheckCapacity(Heap* hp)
{
if (hp->_capacity == hp->_size)
{int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("malloc fail");return;}hp->_a = tmp;hp->_capacity = newcapacity;
}
}
判空
// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}
交换
解析:这里提供了一个swap函数用于向上调整和向下调整时交换数据
//交换
void swap(int* a, int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
插入
每次插入的数据都会进行向上调整,将一串数据建成小堆/大堆
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{CheckCapacity(hp);hp->_a[hp->_size] = x;hp->_size++;Adjustup(hp->_a, hp->_size - 1);
}
向上调整
当插入数据时,注意每次插入一个数据都会向上调整(直到根结点)图中这里只是将结构画了出来助于理解,真实的情况中并不是向右边的堆图一样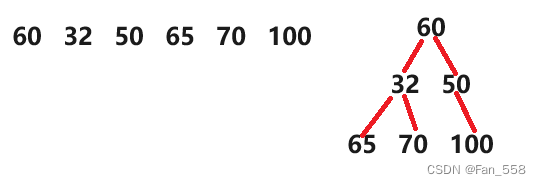
以小堆为例,当a[child] <a[parent]就将二者交换,并将parent 赋值给child,并利用新的child计算出新的parent,这样的做法是可以向上进行调整。这里若是将a[child] <a[parent]变成a[child] >a[parent]就是大堆
//向上调整
void Adjustup(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){swap(a, &a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
删除
解析:需要删除堆顶的数据,但是如果挪动数据删除堆顶的数据,可能会导致可能会导致堆的性质不满足,影响堆的正确性和效率。因此需要交换堆顶与末尾的数据,再将末尾的数据删除,这样一来就可以删除掉堆顶的数据,但是有个问题:将堆尾的数据调整到了堆顶,需要进行向下调整// 堆的删除 删除堆顶
void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));swap(hp->_a, &(hp->_a[0]), &(hp->_a[hp->_size - 1]));--hp->_size;//向下调整AdjustDown(hp->_a, hp->_size, 0);
}
向下调整
解析:当我们删除堆顶数据的时候进行向下调整,n:堆的数据个数,利用parent计算出child下标
//向下调整
void AdjustDown(int* a, int n, int parent)
{//计算左child,相当于(child = leftchild)int child = parent * 2 + 1;//当逐步地向下调整,child会越来越大,child不能超过堆数据个数while (child < n){//向下调整的时候右child可能越界//找左右child小的那一个进行与a[parent]比较if (child + 1 < n && a[child + 1] < a[child]){//若是默认的child(leftchild) > a[child + 1]++child;}//可调整<(小堆)为>(大堆)if (a[child] < a[parent]){swap(a, &a[child], &a[parent]);//向下调整parent = child;child = parent * 2 + 1;}else{break;}}
}
销毁
// 堆的销毁
void HeapDestory(Heap* hp)
{free(hp->_a);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}
获取堆顶数据
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->_a[0];
}
获取个数
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}
小结
本文的分享就到这里啦,如果本文存在疏漏或错误的地方还请您能够指出!
相关文章:

007 数据结构_堆——“C”
前言 本文将会向您介绍关于堆Heap的实现 具体步骤 tips:本文具体步骤的顺序并不是源代码的顺序 typedef int HPDataType; typedef struct Heap {HPDataType* _a;int _size;int _capacity; }Heap;初始化 void HeapCreate(Heap* hp, HPDataType* a, int n) {hp-&…...
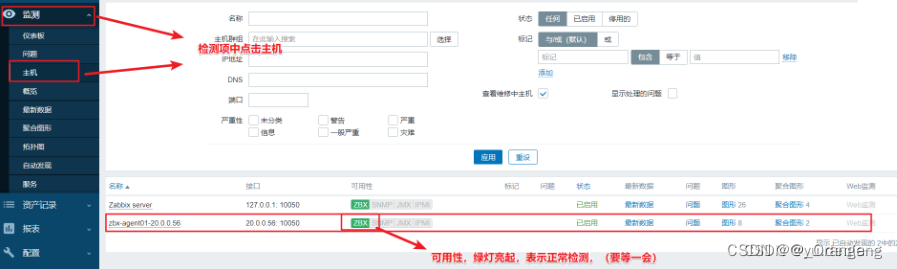
zabbix的原理与安装
一、Zabbix介绍 1、zabbix 是什么? zabbix是一个开源的IT基础监控软件,能实时监控网络服务,服务器和网络设备的状态,如网络使用,CPU负载、磁盘空间等,主要是包括数据的收集、报警和通知的可视化界面zabbi…...
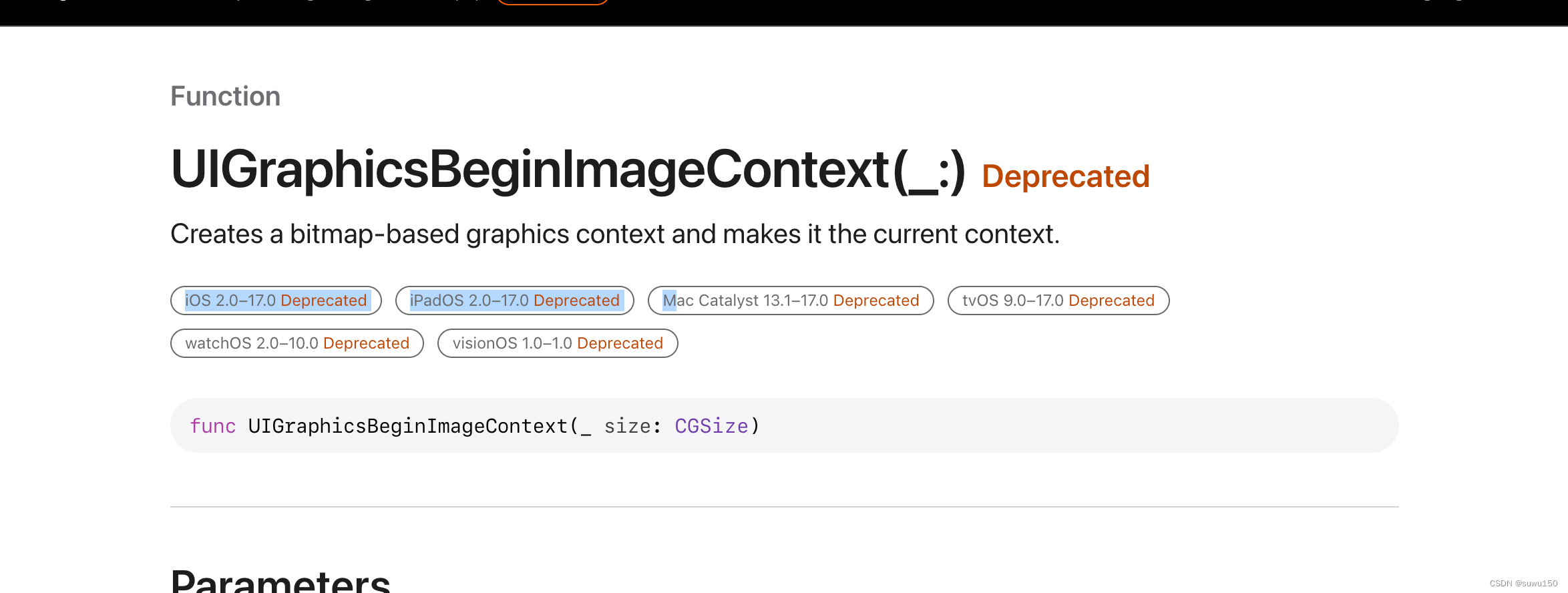
ReactNative中升级IOS 17版本Crash解决
ReactNative中升级IOS 17版本Crash解决 ReactNative中升级IOS 17版本Crash解决一、问题描述二、原因分析三、解决方案决策3.1 设置宽高为非零值3.2 使用新的UIGraphicsImageRenderer替换就版本的UIGraphicsBeginImageContext 四、可能使用到该API的三方库4.1 react-native-fast…...

MongoDB详解
一、MongoDB概述 MongoDB 是一个基于 分布式文件存储 的开源 NoSQL 数据库系统,由 C 编写的。MongoDB 提供了 面向文档 的存储方式,操作起来比较简单和容易,支持“无模式”的数据建模,可以存储比较复杂的数据类型,是一…...

【SpringCloud微服务全家桶学习笔记-服务注册zookeeper/consul】
SpringCloud微服务全家桶学习笔记 Eureka服务注册 gitee码云仓库 9.其他服务注册框架 (1)zookeeper安装与使用 zookeeper需安装在虚拟机上,建议使用CentOS,安装地址如下: zookeeper镜像源 选择第一个进入后下载ta…...

【滑动窗口】LCR 016. 无重复字符的最长子串
LCR 016. 无重复字符的最长子串 解题思路 窗口内的字符串就是不重复子串每次遇到新的字符 看看窗口内是否存在该字符 如果存在直接剔除 然后调整窗口左边界不存在 添加窗口内部 右边界 class Solution {public int lengthOfLongestSubstring(String s) {if(s.length() < …...

C++中将类成员函数作为变量传递给函数
假设类ClassName有一个成员函数 void ClassName::funcname(int);通过typedef定义一个类成员函数指针类型,参数和返回值类型都要与成员函数对应 typedef void (ClassName::*FuncPtr)(int); // 定义类成员函数指针获取到的参数就是 FuncPtr pf...

2024届数字IC设计秋招面经-鼎信
背景 985硕士,计算机科班,实验室做cpu设计和fpga算法加速,我做处理器安全方向,有项目。 投递 8.25 没有笔试,两轮面试,直接通知下周一面试,草草的准备了下。 一面 技术面 9.4 不到半小时 …...
【数据结构】二叉树的节点数,叶子数,第K层节点数,高度,查找x节点,判断是否为完全二叉树等方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
和多层感知机(MLP))
前馈神经网络(FFNN)和多层感知机(MLP)
多层感知器(MLP, Multi-Layer Perceptron)和前馈神经网络(Feed-Forward Neural Network, FFNN)是深度学习中两个经常被使用的术语,它们经常被互换使用。让我们详细地了解这两个术语: 多层感知器 (MLP): M…...
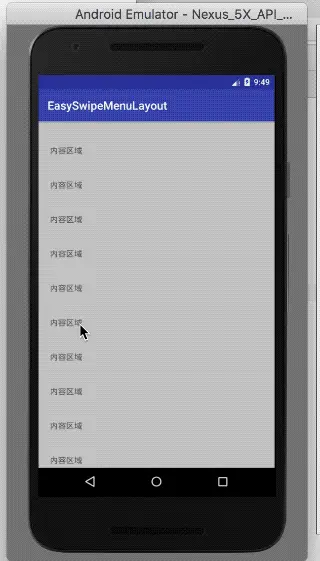
EasySwipeMenuLayout - 独立的侧滑删除
官网 GitHub - anzaizai/EasySwipeMenuLayout: A sliding menu library not just for recyclerview, but all views. 项目介绍 A sliding menu library not just for recyclerview, but all views. Recommended in conjunction with BaseRecyclerViewAdapterHelper Feature…...
优麒麟下载、安装、体验
下载 官网 优麒麟 点击增强版、或者基础版进行下载 虚拟机安装 选择镜像 修改名称和存储路径 设置为50G 下一步,点击完成 开启安装 设置语言 去掉下载更新选项 继续 点击restart now 输入密码 出现下图说明安装成功,可以畅快的使用了...

Appium混合页面点击方法tap的使用
原生应用开发,是在Android、IOS等移动平台上利用官方提供的开发语言、开发类库、开发工具进行App开发;HTML5(h5)应用开发,是利用Web技术进行的App开发。目前,市面上很多app都是原生和h5混合开发,…...

求解灰度直方图,如何绘制灰度直方图(数字图像处理大题复习 P1)
文章目录 1. 画 X 轴2. 画直方图3. Complete 视频原链接 数字图像处理期末考试大题 B站链接 1. 画 X 轴 2. 画直方图 有几个 0 就在图上画多高,同理有几个 1 ,X1 的地方就画多高 3. Complete 这里的情况比较平均,一般来说不会这么平均&a…...

8种结构型设计模式对比
一、适配器模式 简介 适配器模式是一种结构型设计模式,它用于将不兼容的接口转换为可兼容的接口。适配器模式允许两个不兼容的类能够协同工作,通过将一个类的接口转换为另一个类所期望的接口形式。这样就能够在不修改现有代码的情况下,使两…...
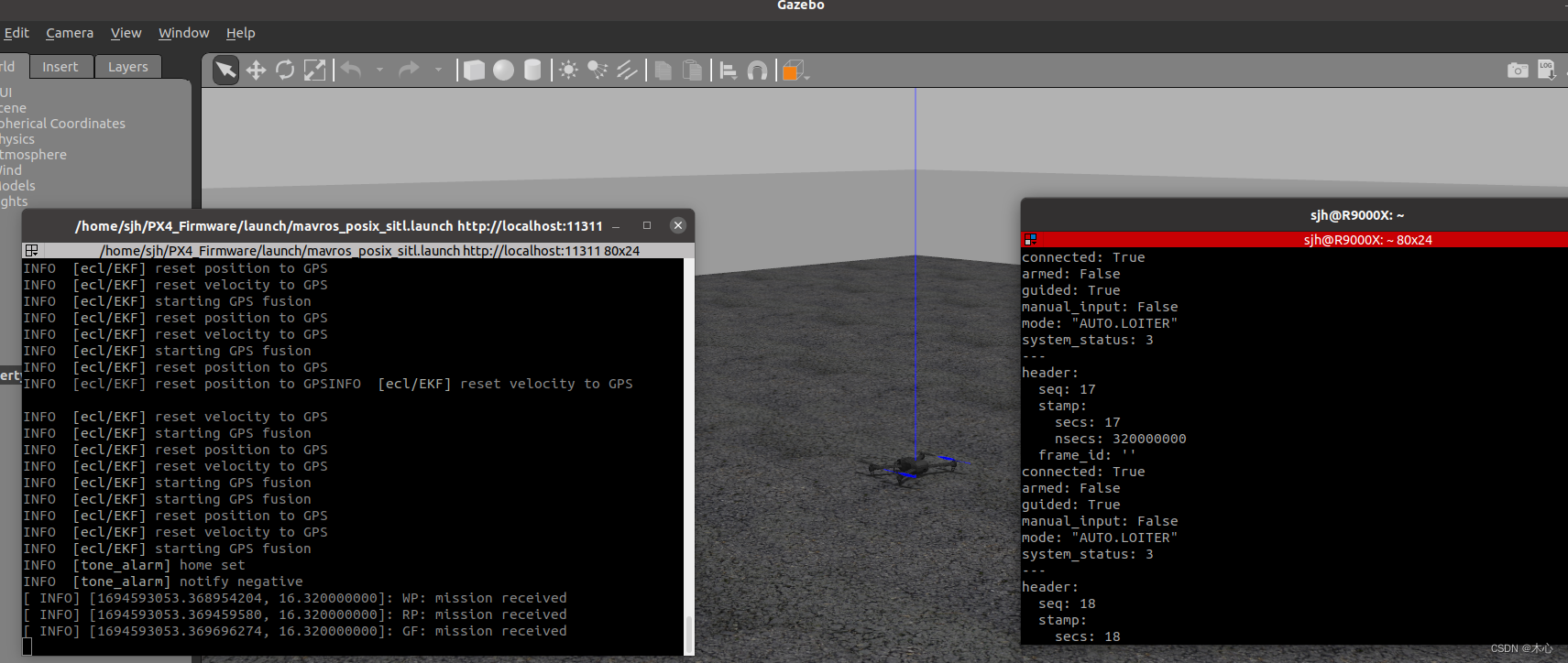
【PX4】Ubuntu20.04+ROS Noetic 配置PX4-v1.12.2和Gazebo11联合仿真环境【教程】
【PX4】Ubuntu20.04ROS Noetic 配置PX4-v-v1.12.2和Gazebo11联合仿真环境【教程】 文章目录 【PX4】Ubuntu20.04ROS Noetic 配置PX4-v-v1.12.2和Gazebo11联合仿真环境【教程】0. 安装UbuntuROS1. 安装依赖2. 安装QGC地面站3. 配置PX4-v1.12.23.1 安装PX43.2 测试PX4是否成功安装…...
msvcp120.dll丢失怎么办?(五种方法快速解决)
首先,让我们来了解一下msvcp120.dll这个文件。msvcp120.dll是一个动态链接库文件,它是Microsoft Visual C 2012 Redistributable Package的一部分。这个文件的作用是支持一些应用程序的运行,例如游戏、办公软件等。当我们在使用这些软件时&am…...

eslint写jsx报错
eslint写jsx报错 ChatGPT提示 在写JSX时,ESLint可能会报出一些语法错误,这些错误通常是由于ESLint默认配置中不支持JSX语法导致的。为了解决这些错误,我们需要在ESLint配置文件中启用对JSX语法的支持。 首先,需要安装eslint-pl…...
最新适合小白前端 Javascript 高级常见知识点详细教程(每周更新中)
1. window.onload 窗口或者页面的加载事件,当文档内容完全加载完成会触发的事件(包括图形,JS脚本,CSS文件),就会调用处理的函数。 <button>点击</button> <script> btn document.q…...
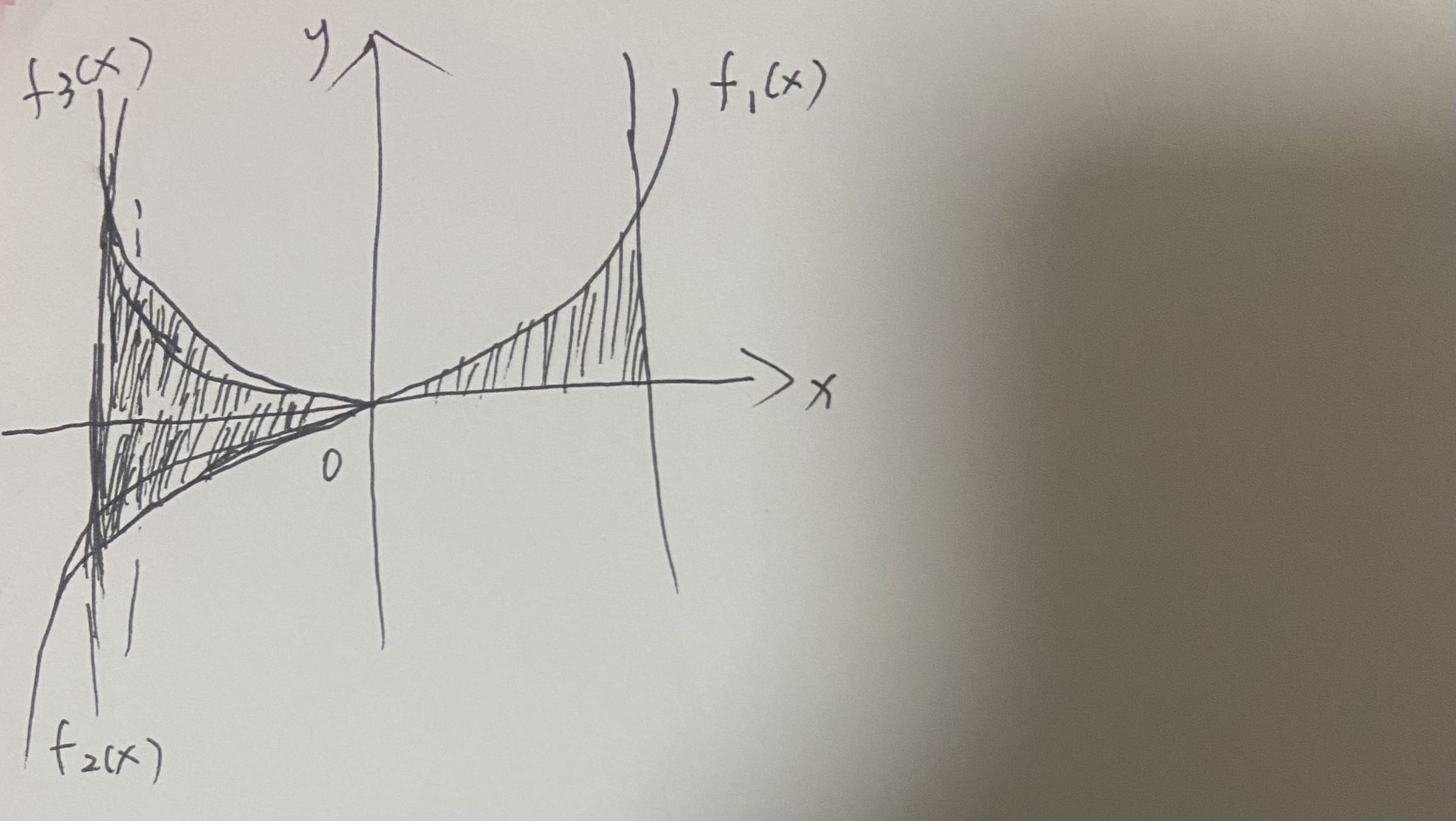
积分值和面积、对称性
积分的基本含义要从积分符号说起,积分号含有加号的意思, ∫ a b f ( x ) d x \int ^b_af(x)dx ∫abf(x)dx可以理解为:区间[a,b]无限细分为无穷多个dx,无穷多个f(x)乘以dx的累积和。根据上面的描述,面积可以理解为 ∫ a b ∣ f (…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
