堆排序(大根堆)
堆的定义如下,n个关键字序列[1...n]称为堆,当且仅当满足:
a(i)>=a(2i)且a(i)>=a(2i+1) 这个为大根堆
a(i)<=a(2i)且a(i)<=a(2i + 1) 这个为小根堆
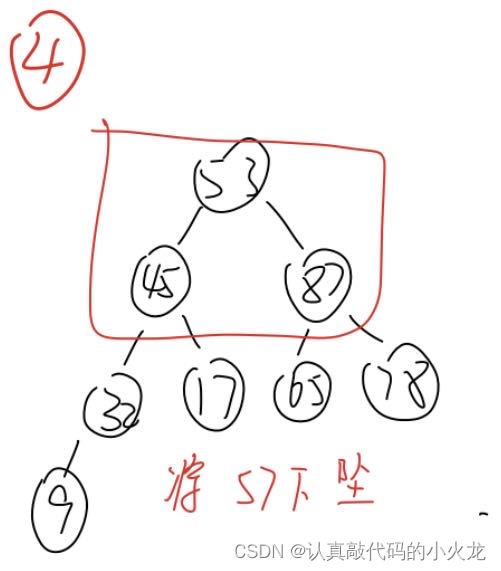
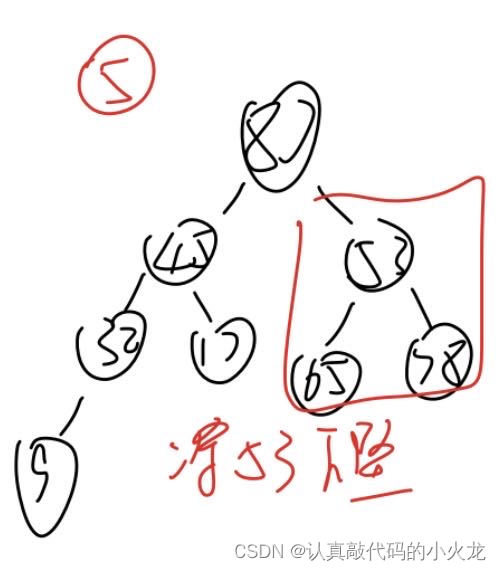
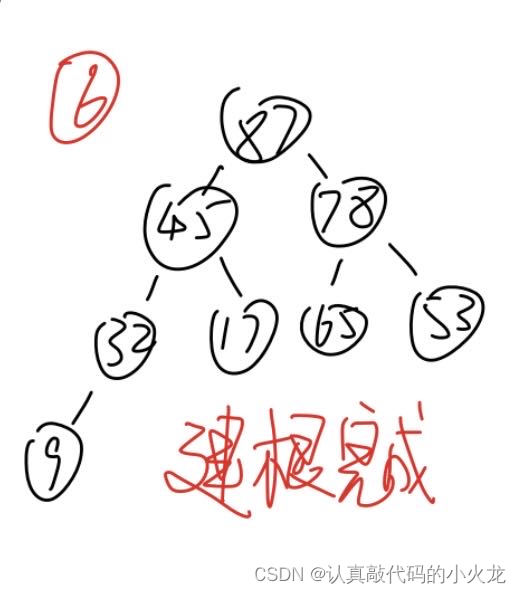
通过建堆得到大根堆
大根堆 87,45,78,32,17,65,53,9 可以看成
87
45 78
32 17 65 53
9
也就相当于是完全二叉树


#include<stdio.h>
void headadjust(int a[], int k, int i);
void swap(int *i, int *j)//交换堆顶和堆底元素
{int temp = *i;*i = *j; *j = temp;
}
void buildmaxheap(int a[], int len)//建立大根堆
{int i = 0;for (i = len / 2; i > 0; i--)//从i=[n/2]~1,反复调整堆headadjust(a, i, len);
}
void headadjust(int a[], int k, int len)//调整堆
{int i = 0;a[0] = a[k];//相当与根节点的复制值for (i = k * 2; i <=len; i *= 2)//从i较大的子节点向下筛选{if (i < len && a[i] < a[i + 1])//左孩子跟右孩子的大小i++;if (a[0] >= a[i])//根结点的值大于左右孩子直接退出break;else{a[k] = a[i];//否则交换孩子与根节点的值k = i;}}a[k] = a[0];//被筛选的值放在最后位置
}
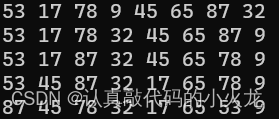
int main()//堆排序
{int i = 0;int a[] = {0,53,17,78,9,45,65,87,32};int sz = sizeof(a) / sizeof(a[0]);printf("原来的数组为\n");for (i = 1; i < sz; i++)printf("%d ", a[i]);buildmaxheap(a, sz-1);//初始建堆for (i = sz-1; i > 1; i--){swap(&a[i], &a[1]);//调用swap()函数交换堆顶和堆底元素,此时堆得性质被破坏headadjust(a, 1, i - 1);//把剩余的i-1个元素整理成堆}printf("\n排完序的数组为\n");for (i = 1; i < sz; i++)printf("%d ", a[i]);return 0;
}

相关文章:

堆排序(大根堆)
堆的定义如下,n个关键字序列[1...n]称为堆,当且仅当满足: a(i)>a(2i)且a(i)>a(2i1) 这个为大根堆 a(i)<a(2i)且a(i)<a(2i 1) 这个为小根堆 通过建堆得到大根堆 大根堆 87,45,78,32,17,65,53,9 可以看成 …...
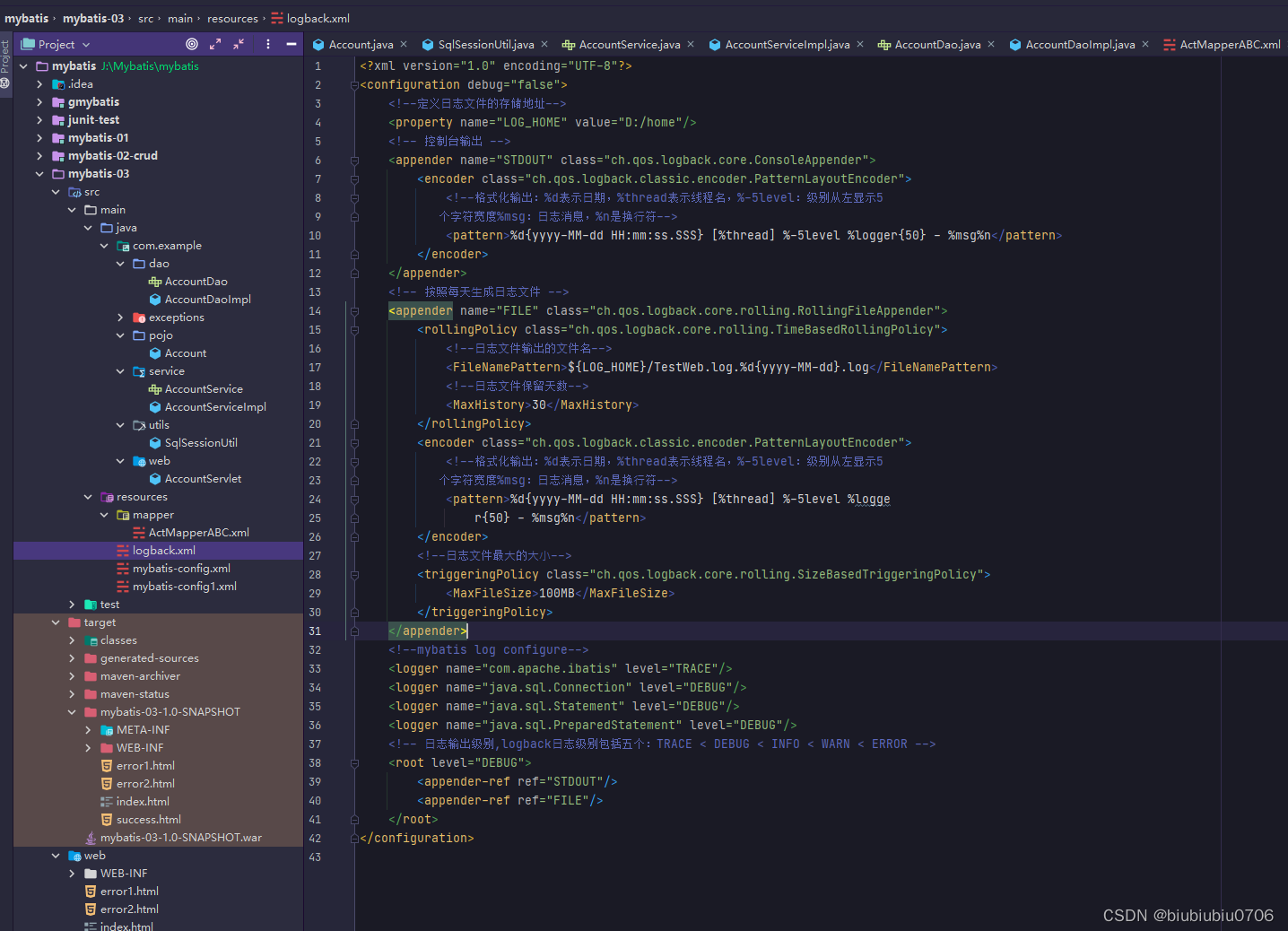
Mybatis学习笔记3 在Web中应用Mybatis
Mybatis学习笔记2 增删改查及核心配置文件详解_biubiubiu0706的博客-CSDN博客 技术栈:HTMLServletMybatis 学习目标: 掌握mybatis在web应用中如何使用 Mybatis三大对对象的作用域和生命周期 关于Mybatis中三大对象的作用域和生命周期、 官网说明 ThreadLocal原理及使用 巩…...

软件测试之功能测试详解
一、功能测试概述 1)功能测试就是对产品的各功能进行验证,根据功能测试用例,逐项测试,检查产品是否达到用户要求的功能。 2)功能测试,根据产品特性、操作描述和用户方案,测试一个产品的特性和…...

javascript选取元素的范围,可以包含父级,也可以不包含父级
//函数可以选取元素的范围,对于要选取文本的非常方便,或选取特定的子节点 function getRange(element){//判断是否支持range范围选取var supdocument.implementation.hasFeature("Range","2.0");var also(typeof document.createRan…...

QGIS怎么修改源代码?持续更新...
修改配置文件保存位置 修改目的:放着和本地安装的其他QGIS共用一份配置文件 修改文件:core/qgsuserprofilemanager.cpp 修改位置:第37行 return basePath QDir::separator() "my_profiles";修改完毕后,再次生成一下…...
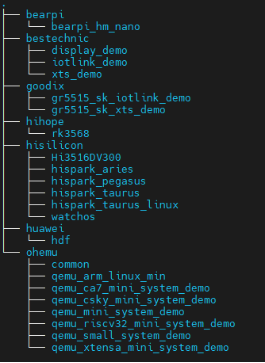
dev board sig技术文章:轻量系统适配ARM架构芯片平台
摘要:本文简单介绍OpenHarmony轻量系统移植,会分多篇 适合群体:想自己动手移植OpenHarmony轻量系统的朋友 开始尝试讲解一下系统的移植,主要是轻量系统,也可能会顺便讲下L1移植。 1.1移植类型 OpenHarmony轻量系统的…...

MyBatis之增删查改功能
文章目录 一、创建各种类二、MyBatis的各种功能 1、查询<select>2、增加<insert>3、修改<update>4、删除<delete>三、总结 前言 在MyBatis项目中编写代码实现对MySql数据库的增删查改 一、创建各种类 1、在Java包的mapper文件下创建一个接口 我创建…...

Leetcode算法入门与数组丨5. 数组二分查找
文章目录 1 二分查找算法2 二分查找细节3 二分查找两种思路3.1 直接法3.2 排除法 1 二分查找算法 二分查找算法是一种常用的查找算法,也被称为折半查找算法。它适用于有序数组的查找,并通过将待查找区间不断缩小一半的方式来快速定位目标值。 算法思想…...
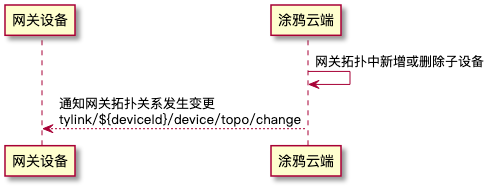
拓扑关系如何管理?
在设备对接涂鸦的云端过程中,一部分设备由于自身资源或硬件配置,无法直接连接云端。而是需要通过网关进行中转,由网关代理实现和云端进行数据交互,间接实现设备接入云端。这样的设备也称为子设备。 要想实现网关代理子设备接入云…...

vue的由来、vue教程和M-V-VM架构思想、vue的使用、nodejs
vue vue的由来 vue教程和M-V-VM架构思想 vue的初步简单使用 nodejs vue的由来 # 1 HTML(5)、CSS(3)、JavaScript(ES5、ES6、ES11):编写一个个的页面 -> 给后端(PHP、Python、Go、Java) -> 后端嵌入模板语法 -> 后端渲染完数据 -> 返回数据给前端 ->…...

课程表 循环依赖 拓扑排序 go语言
学会拓扑排序题目的基本解法 res数组 记录上课顺序g 记录学了课程i 能解锁的课程jindeg 记录每个课程的入度q 记录入度为0的课程 for循环q去解放其他课程 本题来自力扣课程表 func findOrder(numCourses int, prerequisites [][]int) []int {res : []int{}//建一个二维数组记…...

【红包雨接口设计】
一、服务器地址 http://rb.atguigu.cn 二、公共请求头参数 参数名称类型是否必选描述tokenString是用户唯一标识 备注:为了方便我们今天演示,服务端接受所有token。 三、接口 1. 创建红包雨 请求方式:GET请求地址:/api/v1/se…...

SSL证书到期更换证书会影响排名吗?
在现代的数字化时代,网络安全和用户体验成为了网站运营商和开发者们需要高度关注的问题。SSL证书作为一种重要的安全协议,对网站的安全性和用户信任起着至关重要的作用。然而,随着SSL证书的有效期限届满,许多网站运营商面临着更换…...

前端常用库之-JavaScript工具库lodash
文章目录 前端常用库之-JavaScript工具库lodash一、什么是lodash二、安装三、lodash使用Lodash 的 pick() 函数介绍和使用react 实例demo:pick结合...展开运算符(spread operator) 前端常用库之-JavaScript工具库lodash 一、什么是lodash 官网: https:…...
)
Linux- execve()
execve() 是 Linux/UNIX 中的 exec 函数家族中的一个,它允许进程执行一个新的程序。具体地,execve() 替换当前进程的映像为新的程序映像。 函数原型如下: int execve(const char *pathname, char *const argv[], char *const envp[]);pathn…...
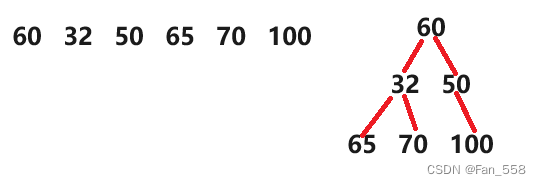
007 数据结构_堆——“C”
前言 本文将会向您介绍关于堆Heap的实现 具体步骤 tips:本文具体步骤的顺序并不是源代码的顺序 typedef int HPDataType; typedef struct Heap {HPDataType* _a;int _size;int _capacity; }Heap;初始化 void HeapCreate(Heap* hp, HPDataType* a, int n) {hp-&…...
zabbix的原理与安装
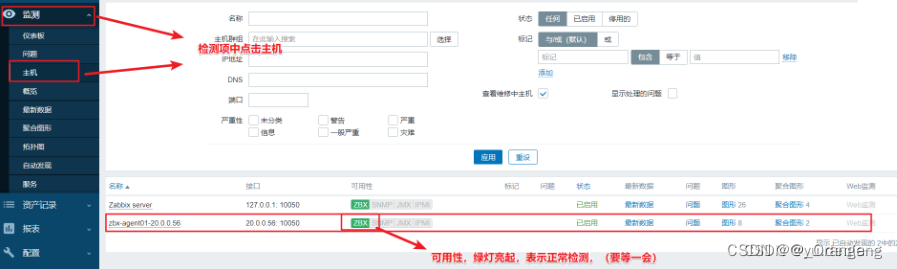
一、Zabbix介绍 1、zabbix 是什么? zabbix是一个开源的IT基础监控软件,能实时监控网络服务,服务器和网络设备的状态,如网络使用,CPU负载、磁盘空间等,主要是包括数据的收集、报警和通知的可视化界面zabbi…...
ReactNative中升级IOS 17版本Crash解决
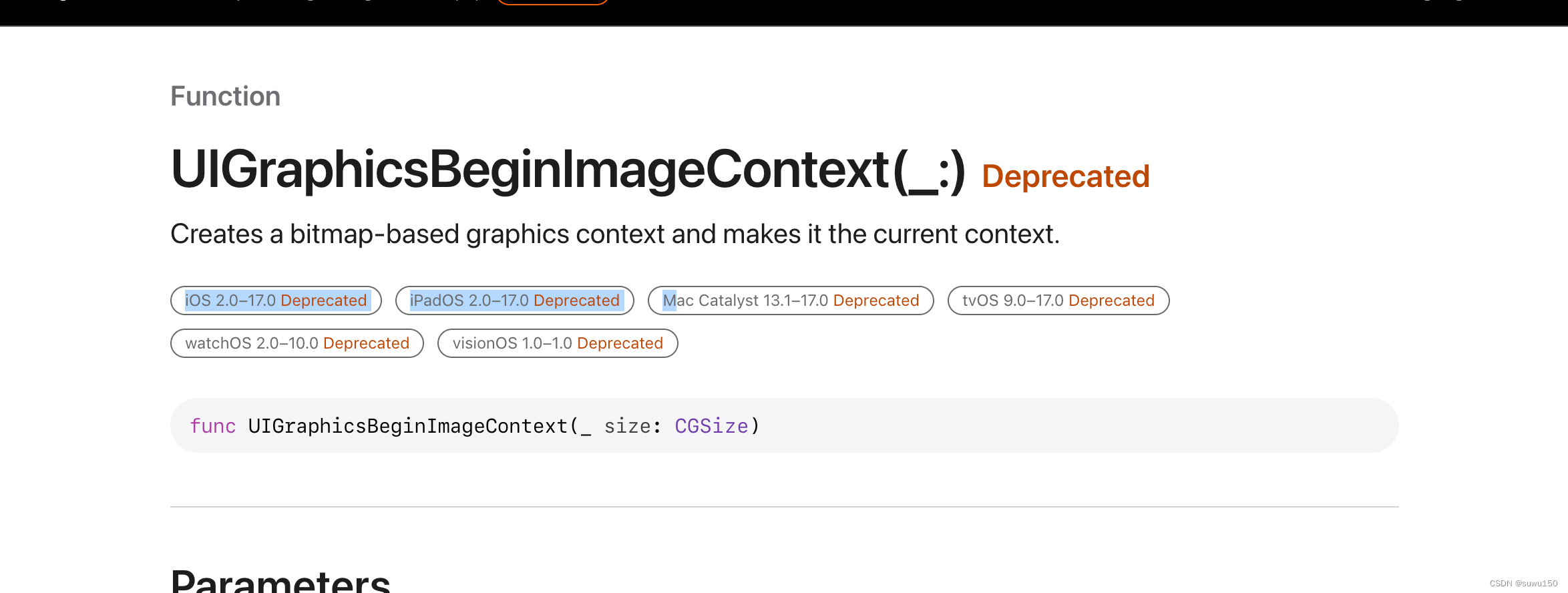
ReactNative中升级IOS 17版本Crash解决 ReactNative中升级IOS 17版本Crash解决一、问题描述二、原因分析三、解决方案决策3.1 设置宽高为非零值3.2 使用新的UIGraphicsImageRenderer替换就版本的UIGraphicsBeginImageContext 四、可能使用到该API的三方库4.1 react-native-fast…...

MongoDB详解
一、MongoDB概述 MongoDB 是一个基于 分布式文件存储 的开源 NoSQL 数据库系统,由 C 编写的。MongoDB 提供了 面向文档 的存储方式,操作起来比较简单和容易,支持“无模式”的数据建模,可以存储比较复杂的数据类型,是一…...

【SpringCloud微服务全家桶学习笔记-服务注册zookeeper/consul】
SpringCloud微服务全家桶学习笔记 Eureka服务注册 gitee码云仓库 9.其他服务注册框架 (1)zookeeper安装与使用 zookeeper需安装在虚拟机上,建议使用CentOS,安装地址如下: zookeeper镜像源 选择第一个进入后下载ta…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
