计算机视觉与深度学习-卷积神经网络-卷积图像去噪边缘提取-卷积-[北邮鲁鹏]
目录标题
- 参考学习链接
- 卷积的定义
- 卷积的性质
- 叠加性
- 平移不变性
- 交换律
- 结合律
- 分配律
- 标量
- 边界填充
- 边界填充方法 - 常数填充最常用
- 常数填充
- 零填充(zero padding)
- 拉伸
- 镜像
- 卷积示例
- 单位脉冲核
- 无变化
- 平移
- 平滑
- 锐化
- 卷积核
- 平均卷积核
- 高斯卷积核
- 高斯卷积核定义
- 高斯卷积核生成步骤
- 高斯核特性
- 卷积核分解的作用(降低算法复杂度)
- 高斯卷积核vs平均卷积核
参考学习链接
计算机视觉与深度学习-04-图像去噪&卷积-北邮鲁鹏老师课程笔记
卷积的定义
在数学和信号处理中,卷积是一种数学运算,用于描述两个函数之间的关系。卷积可以看作是一种加权平均的操作,它将两个函数(通常是一个输入函数和一个响应函数)结合在一起,生成一个新的函数。
卷积运算通常用符号 “*” 表示。给定两个函数 f(x) 和 g(x),它们的卷积定义为:
[ ( f ∗ g ) ( x ) = ∫ − ∞ ∞ f ( τ ) g ( x − τ ) d τ ] [ (f * g)(x) = \int_{-\infty}^{\infty} f(\tau) g(x - \tau) d\tau ] [(f∗g)(x)=∫−∞∞f(τ)g(x−τ)dτ]
或者在离散的情况下,对于离散函数 f[n] 和 g[n],卷积定义为:
[ ( f ∗ g ) [ n ] = ∑ m = − ∞ ∞ f [ m ] g [ n − m ] ] [ (f * g)[n] = \sum_{m=-\infty}^{\infty} f[m] g[n - m] ] [(f∗g)[n]=m=−∞∑∞f[m]g[n−m]]
上述定义中,卷积运算将函数 g(x)(或 g[n])沿着 x 轴(或 n 轴)进行翻转,并与函数 f(x)(或 f[n])逐点相乘,然后对乘积进行积分(或求和)来获得新的函数 (f * g)(x)(或 (f * g)[n])。

卷积后的图像
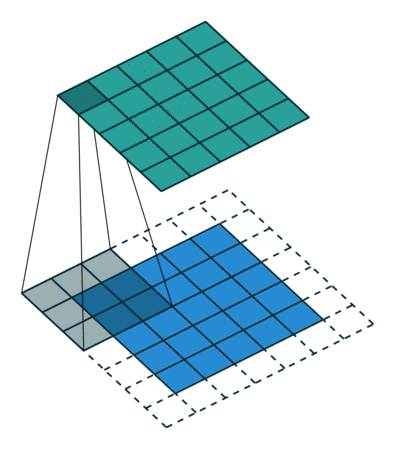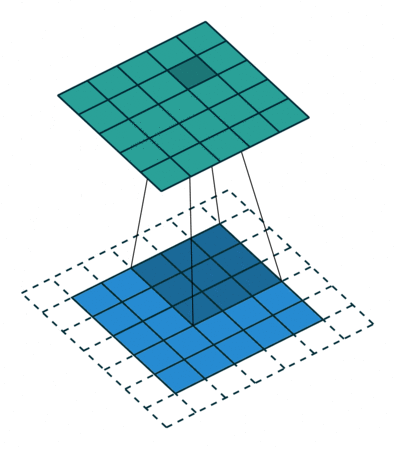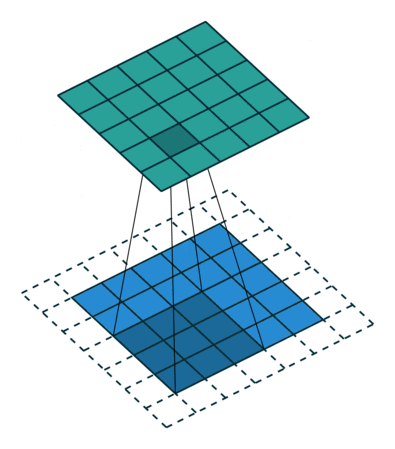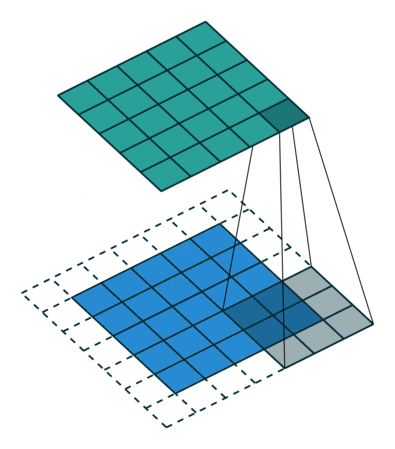
卷积的性质
叠加性
f i l e r ( f 1 + f 2 ) = f i l t e r ( f 1 ) + f i l t e r ( f 2 ) filer(f_1 + f_2) = filter(f_1) + filter(f_2) filer(f1+f2)=filter(f1)+filter(f2)
意味着两个信号(或函数)的卷积等于它们分别进行卷积后再相加。
平移不变性
f i l e r ( s h i f t ( f ) ) = s h i f t ( f i l t e r ( f ) ) filer(shift(f)) = shift(filter(f)) filer(shift(f))=shift(filter(f))
卷积的平移不变性是指在进行卷积操作时,输入信号(或图像)的平移不会影响卷积操作的输出结果。换句话说,如果输入信号发生平移,那么卷积操作的输出也会相应地发生相同的平移。
即卷积以后平移和平移以后再卷积是一样的
交换律
a ∗ b = b ∗ a a * b = b * a a∗b=b∗a
结合律
a ∗ ( b ∗ c ) = ( a ∗ b ) ∗ c a * (b * c) = (a * b) * c a∗(b∗c)=(a∗b)∗c
分配律
a ∗ ( b + c ) = ( a ∗ b ) + ( a ∗ c ) a * (b + c) = (a * b) + (a * c) a∗(b+c)=(a∗b)+(a∗c)
标量
k a ∗ b = a ∗ k b = k ( a ∗ b ) ka * b = a * kb = k (a * b) ka∗b=a∗kb=k(a∗b)
边界填充
为什么必须边界填充?
如果不进行边界填充,卷积结果的图像比原图像小一圈,卷积操作后的图像要小于输入时图像,通过边界填充,可以实现卷积前后图像的尺寸不变。

如果不进行边界填充,则卷积后的图像

边界填充方法 - 常数填充最常用
边界填充是在进行卷积操作时,在输入数据的边界周围添加额外的像素值。
常数填充
常数填充是指在边界上的像素周围添加一个固定的常数值。
常见的常数填充值包括零填充(常数为0)和边界值填充(常数为边界像素值)
具体而言,对于一个输入大小为 M × N 的图像,如果要在每个边界填充 p 个像素,常数填充会在输入图像的边界上添加 p 行和 p 列的像素,其中每个像素的值都是预先设定好的常数。
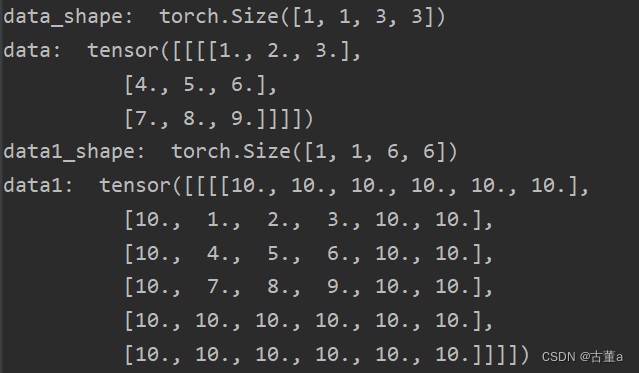
可以看到,分别在左边填充1列10元素,右边填充2列10元素,上边填充1列10元素,下边填充2列10元素。
零填充(zero padding)
零填充是指在边界上的像素周围添加值为零的像素。
具体而言,对于一个输入大小为 M × N 的图像,如果要在每个边界填充 p 个像素,则零填充会在输入图像的边界上添加 p 行和 p 列的零像素,使得填充后的图像大小变为 (M + 2p) × (N + 2p)
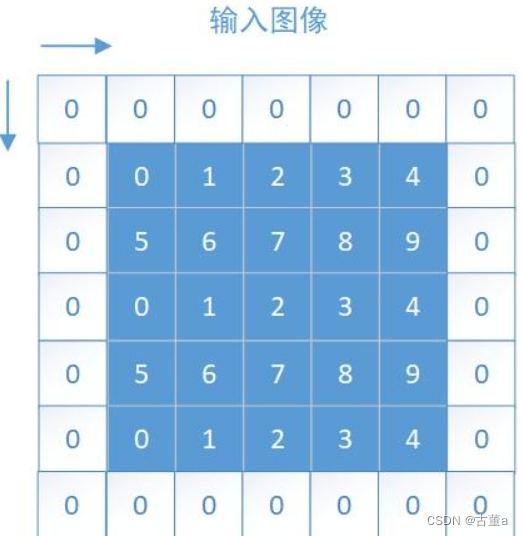
在零填充中,边界上添加的零像素值不包含任何信息,因此不会对卷积操作的结果产生影响。
零填充的主要目的是在进行卷积操作时,确保边缘像素有足够的邻域信息参与计算,从而避免边缘信息丢失。
拉伸
拉伸填充是指在边界上的像素值进行拉伸,使其扩展到填充区域。
具体而言,对于一个输入大小为 M × N 的图像,如果要在每个边界填充 p 个像素,则拉伸填充会将边界上的像素值复制或拉伸到填充区域,使得填充后的图像大小变为 (M + 2p) × (N + 2p)。

拉伸填充的目的是在进行卷积操作时,确保边缘像素有足够的邻域信息参与计算,避免边缘信息丢失。这对于保留输入数据的空间维度和边缘特征非常重要。
拉伸填充还可以防止卷积后输出特征图的尺寸缩小过快,使得网络能够在更多的空间位置上进行计算。
镜像

卷积示例
单位脉冲核
无变化
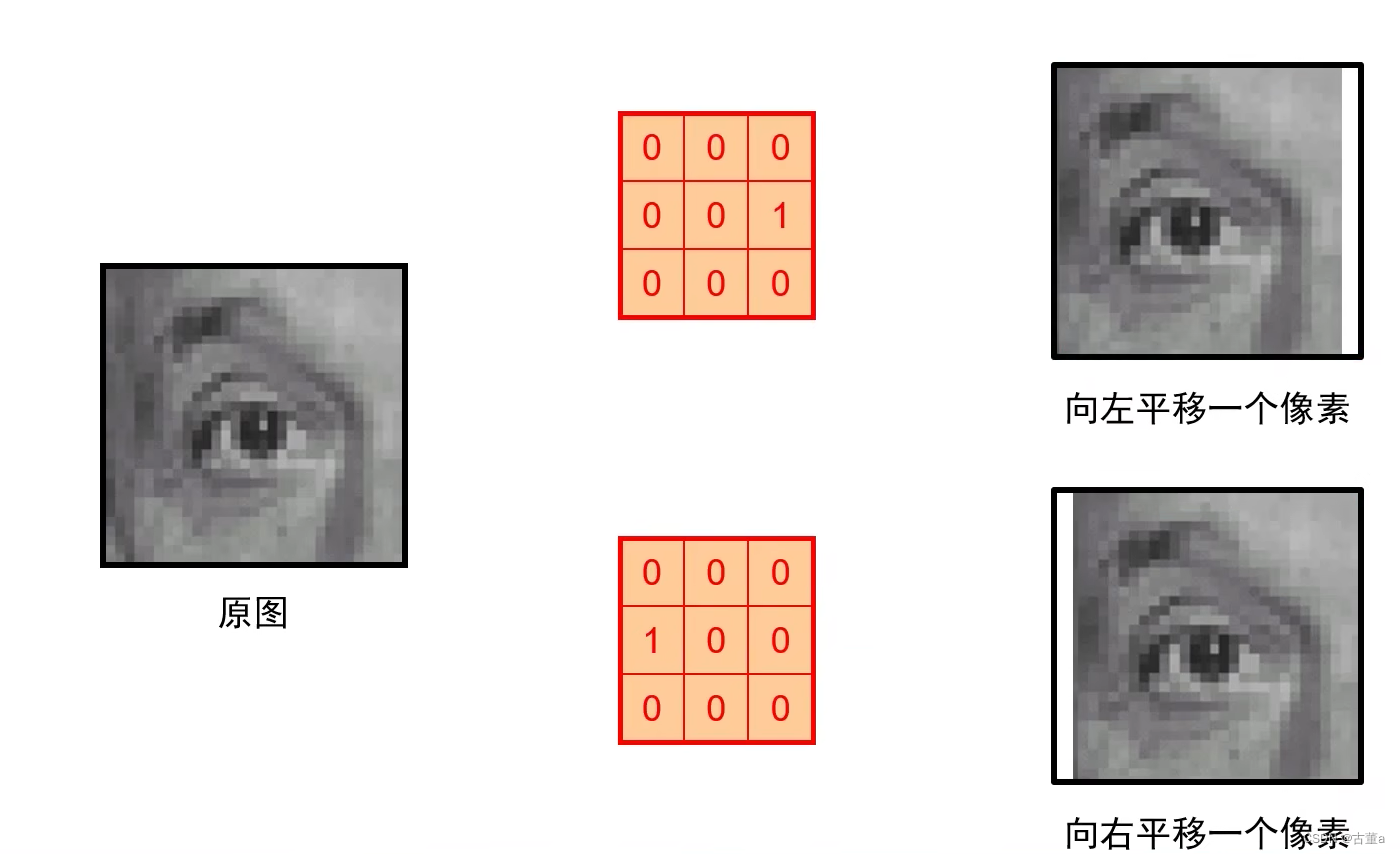
平移
平滑
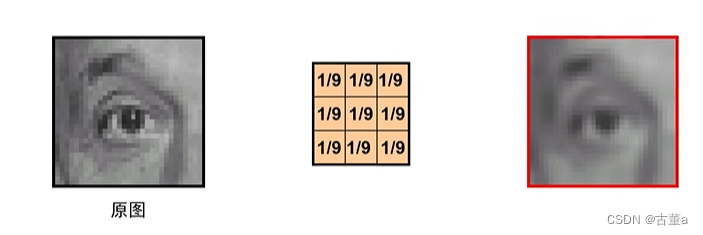
锐化
原图 - 平滑后的图 = 边缘图
在边缘处,原始图像中的像素值与平滑后的图像中的像素值之间存在较大的差异,因此在边缘图中会显示出明显的边缘。

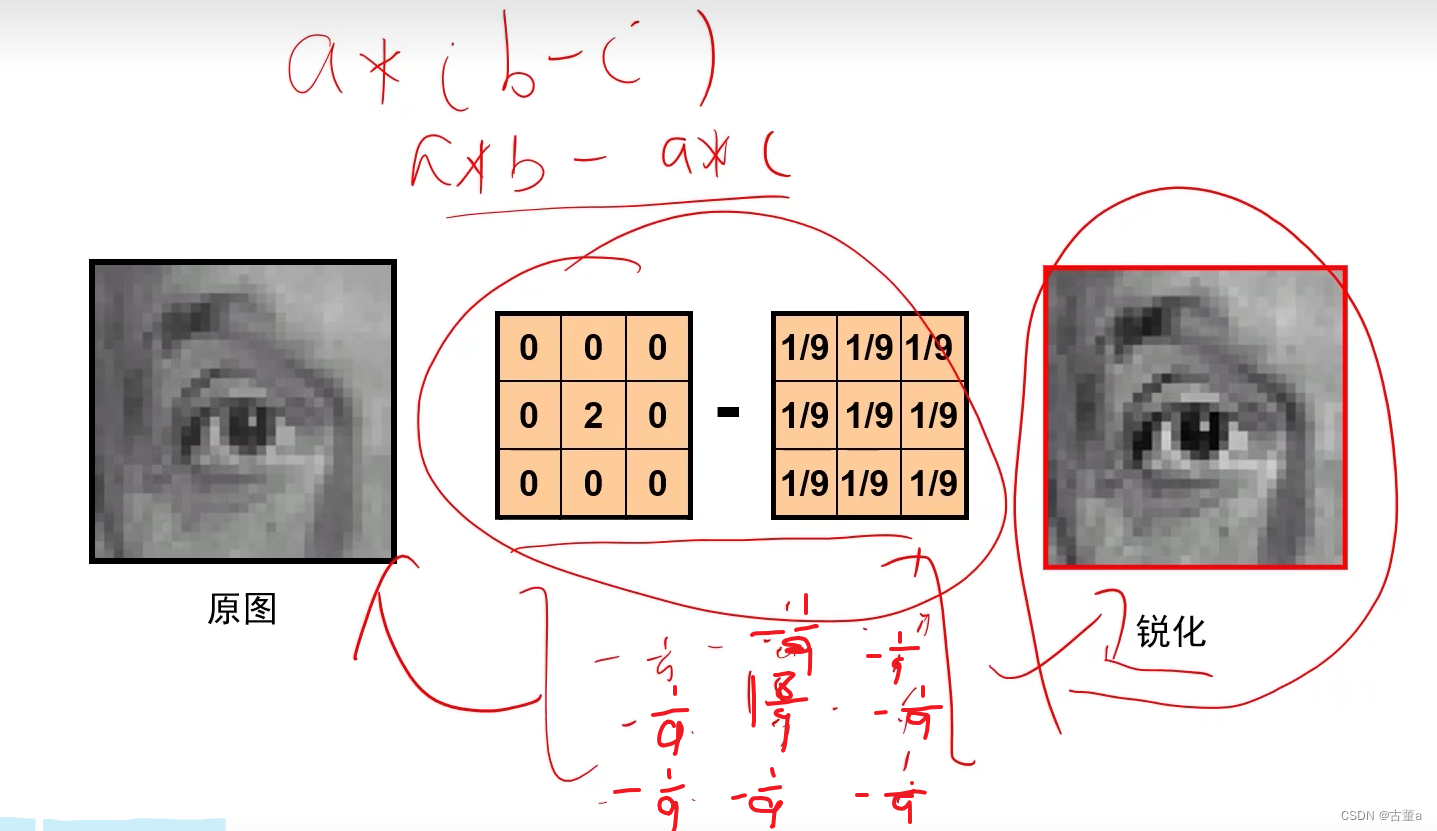
原图 + 边缘图 = 锐化

将原式进行分解
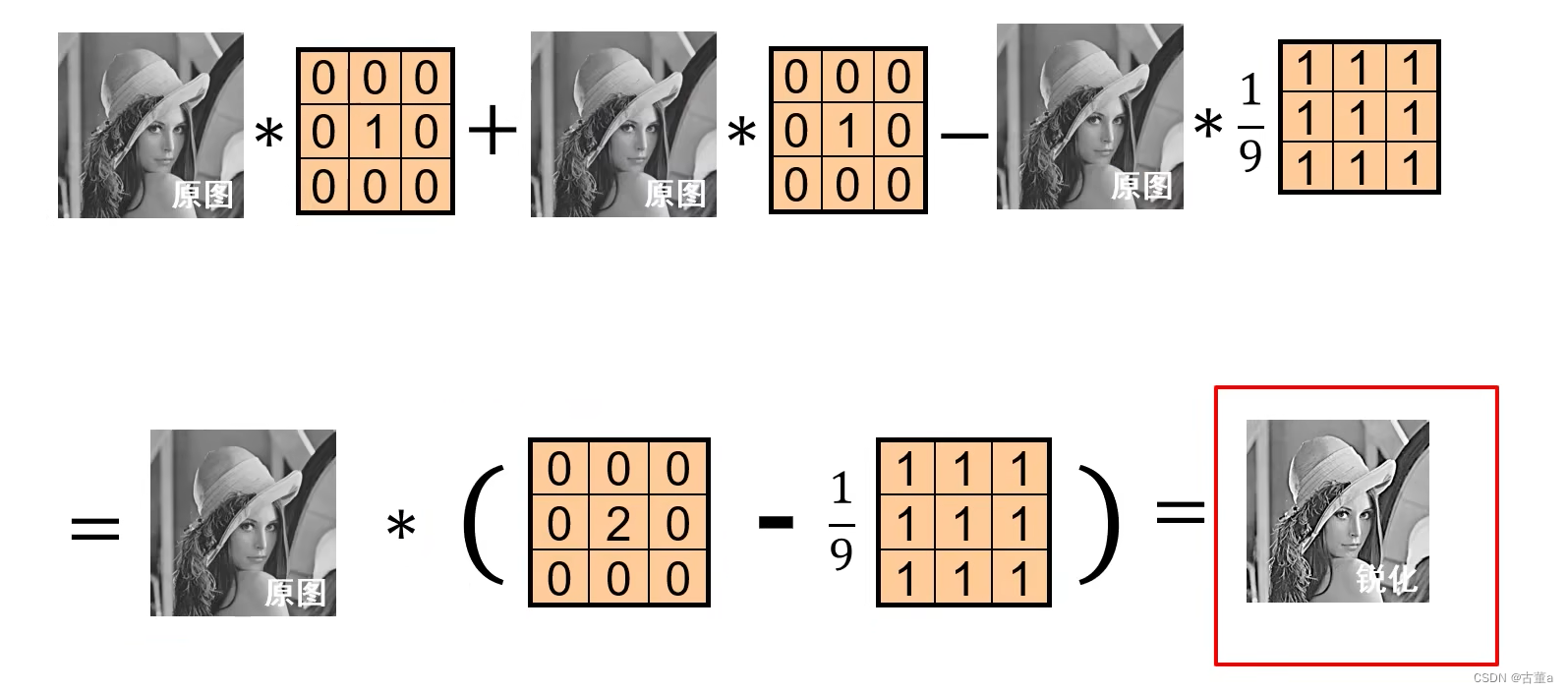
卷积核
平均卷积核
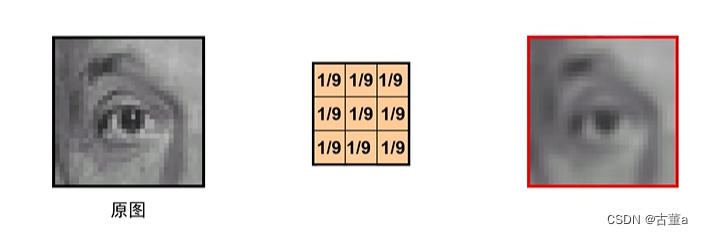
平均卷积核存在的问题

因为是与周围加权平均,所以卷积后的图像产生了一些水平和竖直方向的条状。 振铃!
其实对于平滑来说,卷积核中权重全都是1/9 ,显然这是不合理的。在这个过程中会损失图像的高频信息产生振铃效应。也就是卷积后的图像产生了一些水平和竖直方向的条状纹路。
图像处理中,对一幅图像进行滤波处理,若选用的滤波器具有陡峭(方的,不平滑)的变化,则会使滤波图像产生“振铃”,所谓“振铃”,就是指输出图像的灰度剧烈变化处产生的震荡,就好像钟被敲击后产生的空气震荡。
解决方法:根据邻域像素与中心的远近程度分配权重
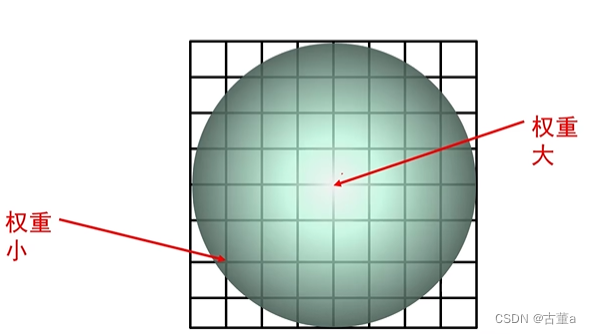
距离中心位置越远相应的权重就应该更小。这样的设置也更加合理一些。这就是 高斯核。
高斯卷积核
高斯卷积核定义
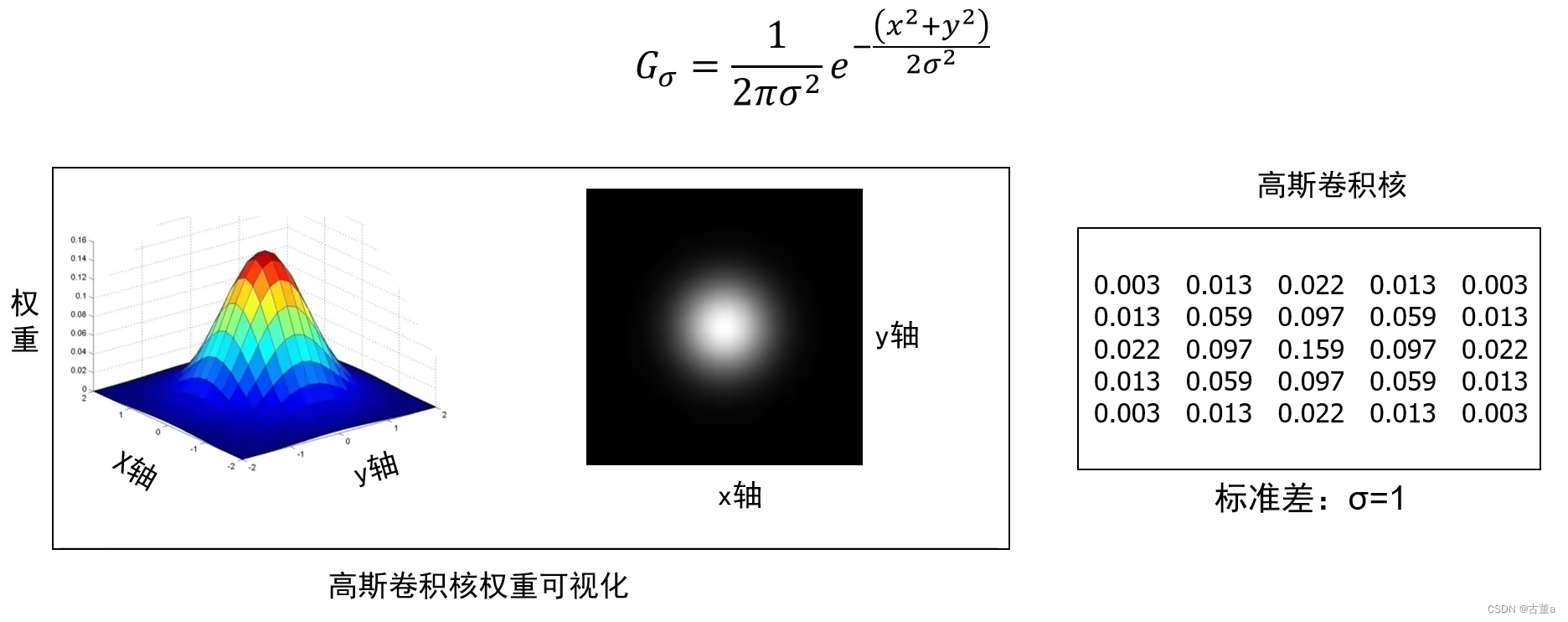
高斯卷积核生成步骤

1. 确定卷积核的尺寸
比如5x5
2. 设置高斯函数的标准差
比如σ=1
3. 计算卷积核各个位置权重值
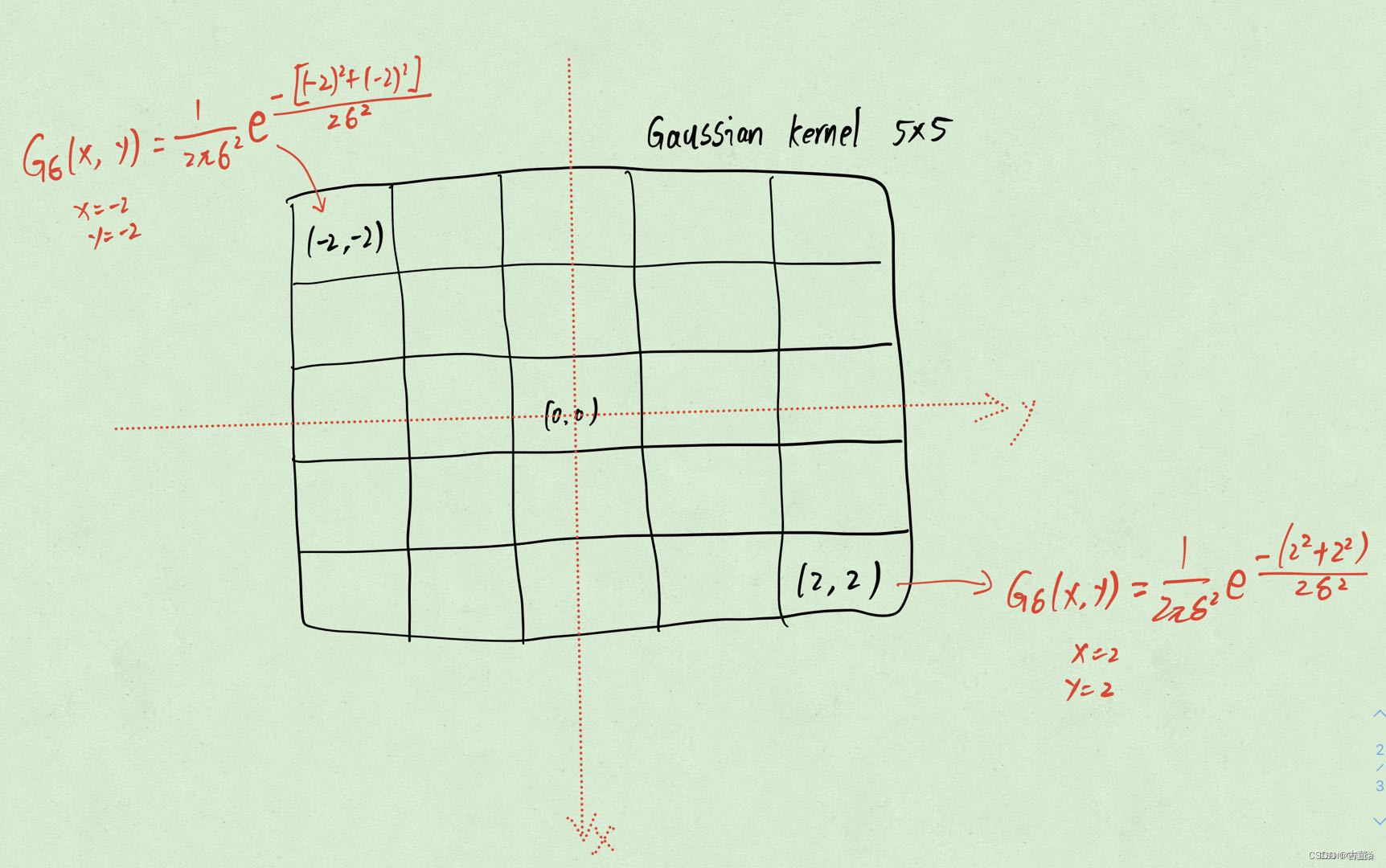
4. 对权重值进行归一化
需要注意的是在高斯核中,约束条件是所有权重相加和为1,这样做的目的是防止卷积后数据的衰减和溢出,因为无论RGB还是灰度图都在[0,255]内。
为什么要对权重值进行归一化?- 防止像素值的衰减和放大
-
如果所有权重的和小于1,假如是一张全白的图也即是像素值全为255,经过一个3×3 ,权重和不是1而是0.1的卷积核,得到输出结果却是25.5 ,显然这也不是想要的结果。
-
如果所有权重的和大于1,卷积后数据溢出(像素值被放大),改变了图像原始的0-255的范围。
只有所有权重的和等于1,卷积后的像素值范围不会改变。
因此,为解决该问题只需要将卷积核归一化即可,也就是卷积核中每一个值除以卷积核权重的总和,添加限制条件为权重和为1 。
高斯卷积核参数
高斯卷积核参数只有一个,高斯函数标准差σ。窗口尺寸可以由高斯函数标准差σ求出。窗口大小 = 23σ+1。
卷积核尺寸大小(窗口大小)
一般由高斯函数标准差σ求出。左边三倍的方差,右边三倍的方差,再加上自身
窗口大小 = 2 × 3 × σ + 1 。 窗口大小=2×3×σ+1。 窗口大小=2×3×σ+1。
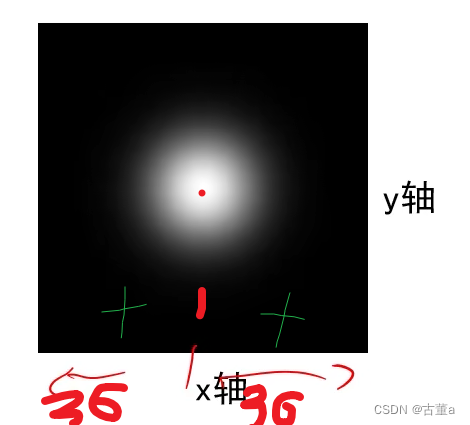
高斯函数标准差σ
其实就是标准差(方差),越大就会散布的越开,也即是窗宽相同,σ越大越扁,σ越小越突出,因为总面积要为1。
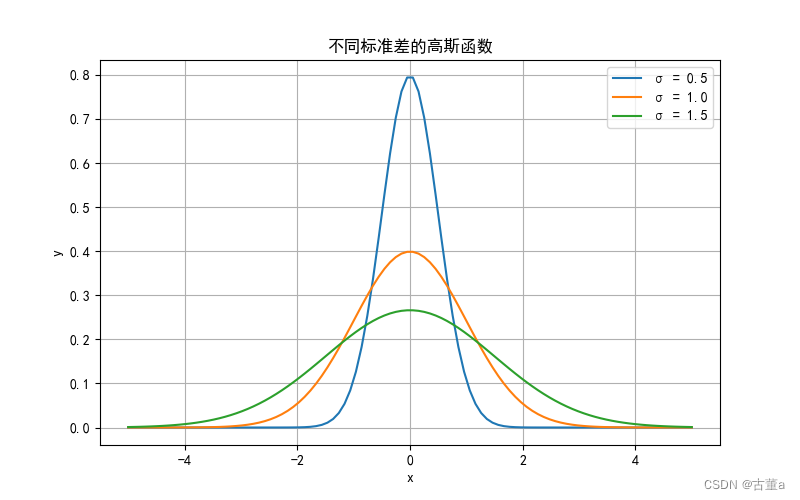
窗宽相同,总面积都为1,则
- 方差越大,中心权重越小,图像越平滑。
- 方差越小,中心权重越大,图像越陡峭。
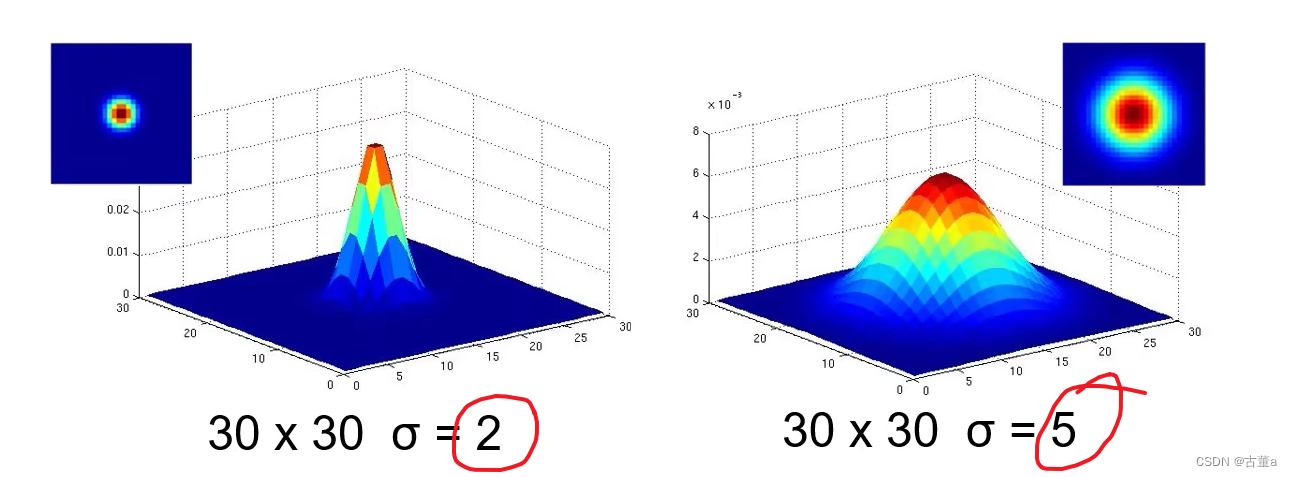
窗宽尺寸
同理,也可以通过固定方差σ去改变窗口大小。
当方差固定时,也就是说这个突出的最高中心点位置是相同的,而总面积又是相同的,归一化操作为(当前值/所有值之和),则
- 窗口越大,归一化中分子相同,分母越大,中心点权重占比越小,相对周围点权重占比越大,越平滑。
- 窗口越小,归一化中分子相同,分母越小,中心点权重占比越大,相对周围点权重占比越小,越陡峭。
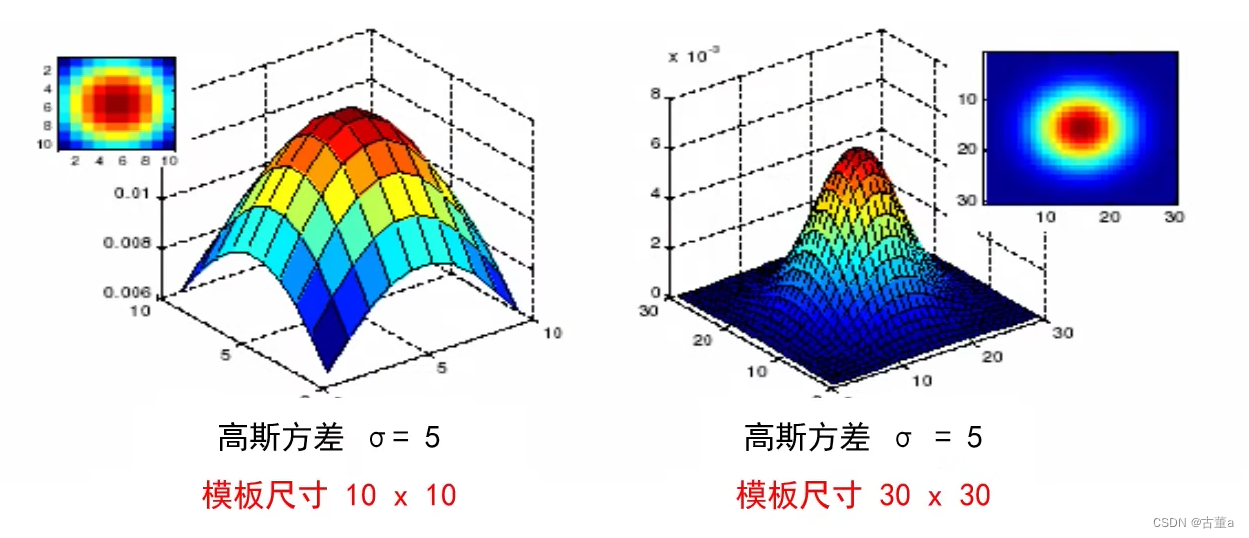
也就是说当方差固定时,窗口越小平滑的就越不明显,就会导致图像比较模糊。
这样一来,就会涉及到两个参数的选取问题,一般来说有个经验性的值。窗口大小为6σ+1。
高斯卷积核参数经验法则

为什么高斯卷积核窗口大小是23σ+1?
-
遵循3σ原则,基本可以包含99%以上的信号,甚至可以不用归一化。超过[-3σ,3σ]范围的信号很少。
-
高斯卷积核中心的左边和右边遵循3σ原则,所以是2x3σ,再加上自身1,所以是2x3xσ+1。
高斯核特性
1、去除图像中的“高频”成分(低通滤波器)
2、两个高斯卷积核卷积后得到的还是高斯卷积核
-
使用多次小方差卷积核连续卷积,可以得到与大方差卷积核相同的结果
-
使用标准差为 σ 的高斯核进行两次卷积与使用标准差 σ 2 \sqrt{2} 2的高斯核进行一次卷积相同
高斯卷积对一副图像进行连续两次σ=1的高斯卷积输出结果等价于使用σ 2 \sqrt{2} 2的高斯卷积一次的输出结果。这个满足勾股定理。
比如连续两次的高斯卷积核大小为2 σ ,3 σ 可以使用σ 2 2 + 3 2 \sqrt{2 ^ 2 + 3 ^ 2} 22+32 的卷积核代替。

3、可分离
可分解为两个一维高斯的乘积
举个例子解释高斯核分解,假设有一个高斯卷积核与一个3x3大小的图像卷积(不考虑边界填充)得到应该是一个点。那么此时将高斯核拆解为两个一维向量,分别与图像进行卷积操作。它的主要作用就是加速。
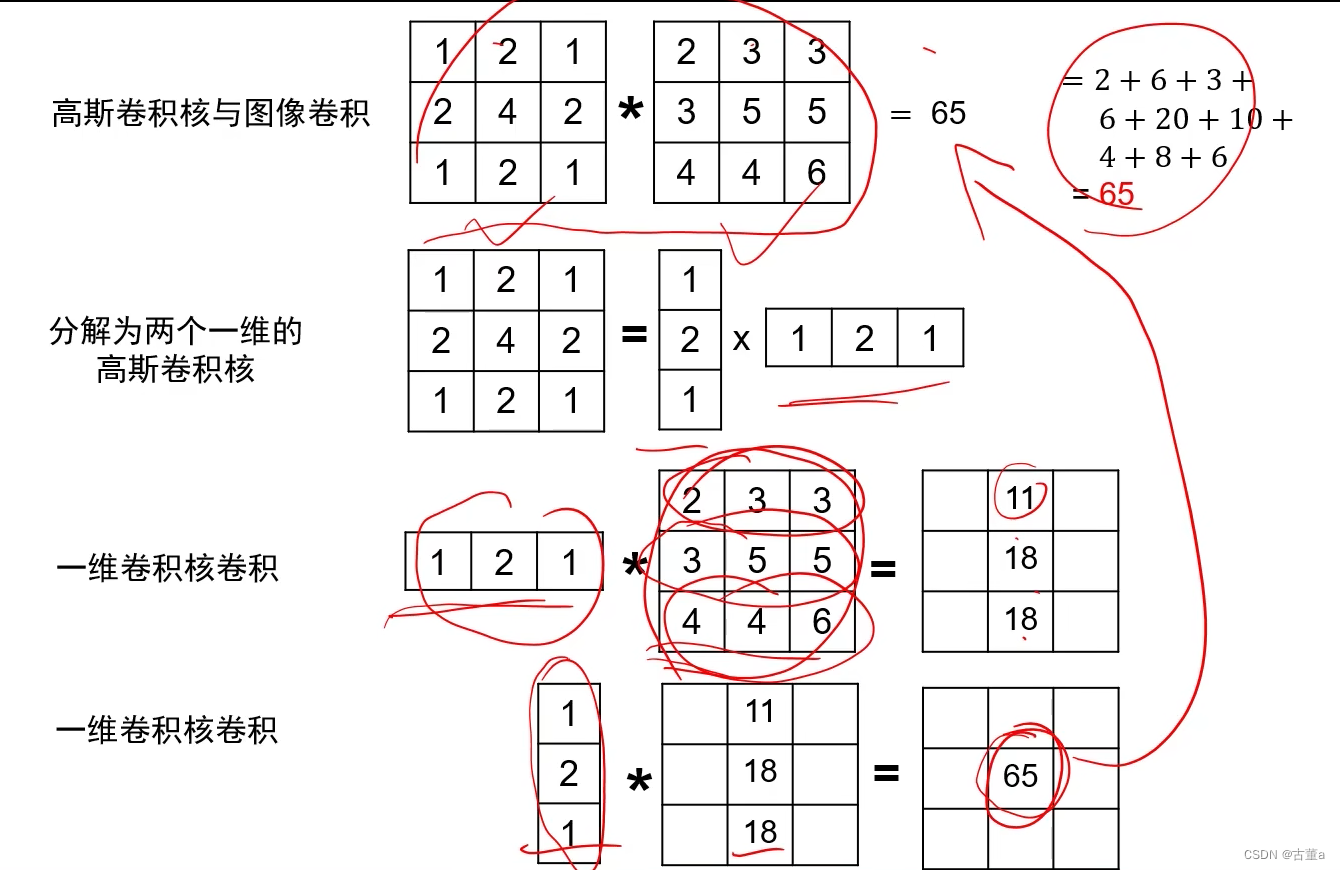
上图中的一维卷积核卷积不是向量乘矩阵,是进行卷积操作。
卷积核分解的作用(降低算法复杂度)
如果使用一个 m x m的卷积核对一幅n x n大小的图像进行卷积,考虑边界填充,算法复杂度为 O ( n 2 m 2 ) O(n^{2} m^{2}) O(n2m2)
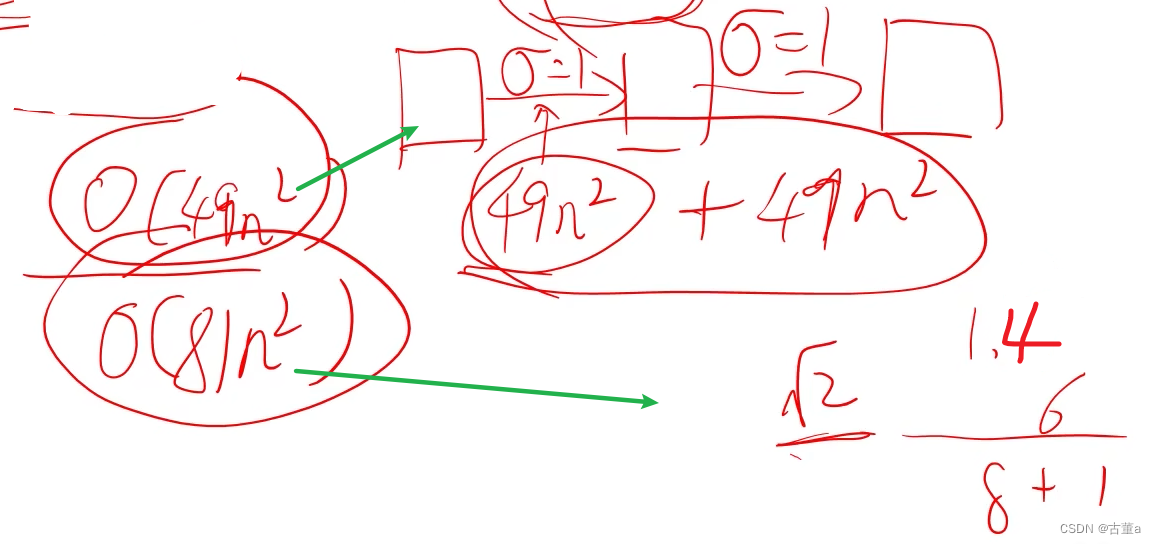
使用分解卷积算法复杂度 O ( n 2 m ) O(n^{2} m) O(n2m)【其实这是x或者y一个方向上的复杂度】,也就是说如果对核进行分离,那么复杂度就能够降低一个等级,这是一件很有意义的事情。
从这里也可以看出来如果使用小核进行卷积也能够加速运算。
高斯卷积核vs平均卷积核

相关文章:

计算机视觉与深度学习-卷积神经网络-卷积图像去噪边缘提取-卷积-[北邮鲁鹏]
目录标题 参考学习链接卷积的定义卷积的性质叠加性平移不变性交换律结合律分配律标量 边界填充边界填充方法 - 常数填充最常用常数填充零填充(zero padding)拉伸镜像 卷积示例单位脉冲核无变化平移平滑锐化 卷积核平均卷积核高斯卷积核高斯卷积核定义高斯…...

JS手动实现发布者-订阅者模式
发布-订阅模式是一种对象间一对多的依赖关系,当一个对象的状态发送改变时,所有依赖于它的对象都将得到状态改变的通知。具体过程是:订阅者把自己想订阅的事件注册到调度中心,当发布者更新该事件时通知调度中心,由调度中…...

【含面试题】MySQL死锁日志分析与解决的Java代码实现
AI绘画关于SD,MJ,GPT,SDXL百科全书 面试题分享点我直达 2023Python面试题 2023最新面试合集链接 2023大厂面试题PDF 面试题PDF版本 java、python面试题 项目实战:AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI…...

解决方案:TSINGSEE青犀+智能分析网关助力智慧仓储智能化监管
为全面保障物流仓储的安全性与完整性,解决仓库管理难题,优化物流仓储方式,提升仓储效率,降低人工成本,旭帆科技推出智慧仓储AI视频智能分析方案,利用物联网、大数据、云计算等技术,对仓储管理进…...
进程间通信
#include <unistd.h> int pipe(int pipefd[2]); 功能:创建一个匿名管道,用于进程间通信 参数: -int pipefd[2]:传出参数 pipefd[0]对应的是管道的读端 pipefd[0]对应的是管道的写端 返回值: 成功返回0,失败返回-…...
Ubuntu 22.04.3 LTS安装
最近换电脑了,准备重新装一下ubuntu。多年前装过ubuntu很老的版本,现在发现官网最新的LTS版本是 Ubuntu 22.04.3 LTS 版本。那重新装的话,肯定装最新的版本了。这里我记录下自己的安装过程,作为以后的笔记查看。 我的环境&#x…...
记一次manjaro-i3系统sogoupinying候选词无法正常显示中文(变方框了)问题解决方案
记一次manjaro-i3系统sogoupinying候选词无法正常显示中文(变方框了)问题解决方案 前言解决方案 前言 今天早上发现公司电脑显卡驱动好像坏了,各种折腾完了干脆把系统搞黑屏无法开机了,时间有限懒再修了,于是重装了系…...

Lua学习笔记:词法分析
前言 本篇在讲什么 Lua的词法分析 本篇需要什么 对Lua语法有简单认知 对C语法有简单认知 依赖Visual Studio工具 本篇的特色 具有全流程的图文教学 重实践,轻理论,快速上手 提供全流程的源码内容 ★提高阅读体验★ 👉 ♠ 一级标题…...
flask服务鉴权
基本认证(Basic Authentication): 这是一种简单的鉴权方式,需要客户端发送用户名和密码,服务器验证后允许或拒绝访问。可以使用 Flask-BasicAuth 扩展来实现。首先,安装扩展: pip install Fla…...
【2023华为杯B题】DFT类矩阵的整数分解逼近(思路及代码下载)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

基于微信小程序的校园生活管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言运行环境学生微信端的主要功能有:管理员的主要功能有:具体实现截图视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝1…...

SQL server 创建存储过程
SQL Server如何创建存储过程 存储过程: 可以理解为完成特定功能的一组 SQL 语句集,存储在数据库中,经过第一次编译,之后的运行不需要再次编译,用户通过指定存储过程的名字并给出参数(如果该存储过程带有参数…...
一文了解亚马逊云科技适用于 Amazon Lightsail 的托管数据库
Amazon Lightsail 是亚马逊云科技提供的一种易上手使用、月度价格经济实惠,并包括了计算实例、容器、存储、数据库的虚拟专用服务器。在创建时可以进行业务蓝图选择,可选择包含多种操作系统(Linux/Windows 等)或操作系统加上典型应…...
)
【antd Col】奇怪的TypeError: Cannot read properties of undefined (reading ‘then‘)
现象 修改antd的Col组件的layouts属性为span后,并通过监听resize事件对span列宽进行动态变化时,报错TypeError: Cannot read properties of undefined (reading ‘then‘)。 补充示例一 由于我使用了飞冰ice.js,且在以下过程中写了如下语句…...

requests处理 multipart/form-data 请求以及 boundary值问题
requests处理 multipart/form-data 请求以及 boundary值问题 前言1. 请求需要携带本地资源2. 请求需要携带json3. 总结 前言 关于 Content-type: multipart/form-data可以看一下这篇文章, 分析特别详细 HTTP协议之multipart/form-data请求分析 put和post区别不大, 只是上传资…...
FBX文件结构解读【文本格式】
FBX 格式几乎受到所有 3D 引擎的支持,是 Autodesk 开发的 3D 模型的专有格式。它支持顶点、索引、法线、UV坐标、材质和动画。 FBX还支持许多其他类型的信息,但它们对游戏引擎几乎没有用处。 推荐:用 NSDT编辑器 快速搭建可编程3D场景 有两种…...
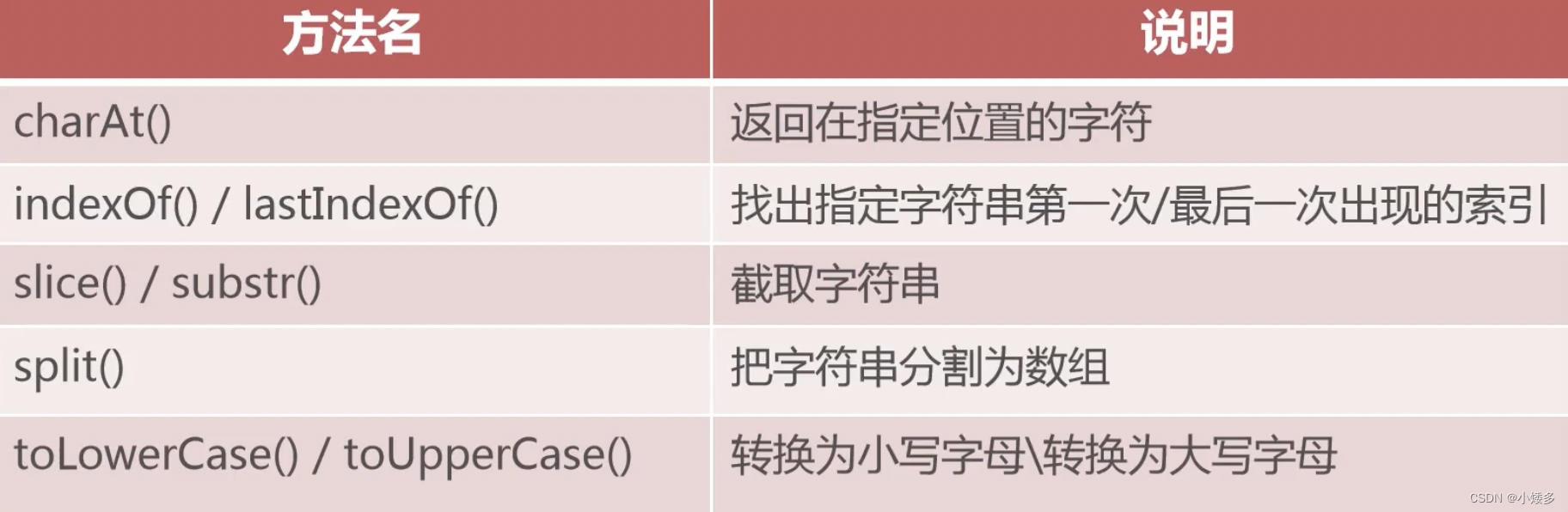
JS基础语法
JS是一门面向对象的编程语言,运行在客户端的脚本语言,可以基于Node.js进行服务器端编程 JS的作用: 表单动态校验网页特效服务端开发 浏览器执行JS: 浏览器分为两部分:渲染引擎和JS引擎 渲染引擎用来解析HTML和CSS,…...

【Zabbix监控一】zabbix的原理与安装
利用一个优秀的监控软件,我们可以: ●通过一个友好的界面进行浏览整个网站所有的服务器状态 ●可以在 Web 前端方便的查看监控数据 ●可以回溯寻找事故发生时系统的问题和报警情况 总结:zabbix主要功能 监控,cpu负载,内存使用&a…...
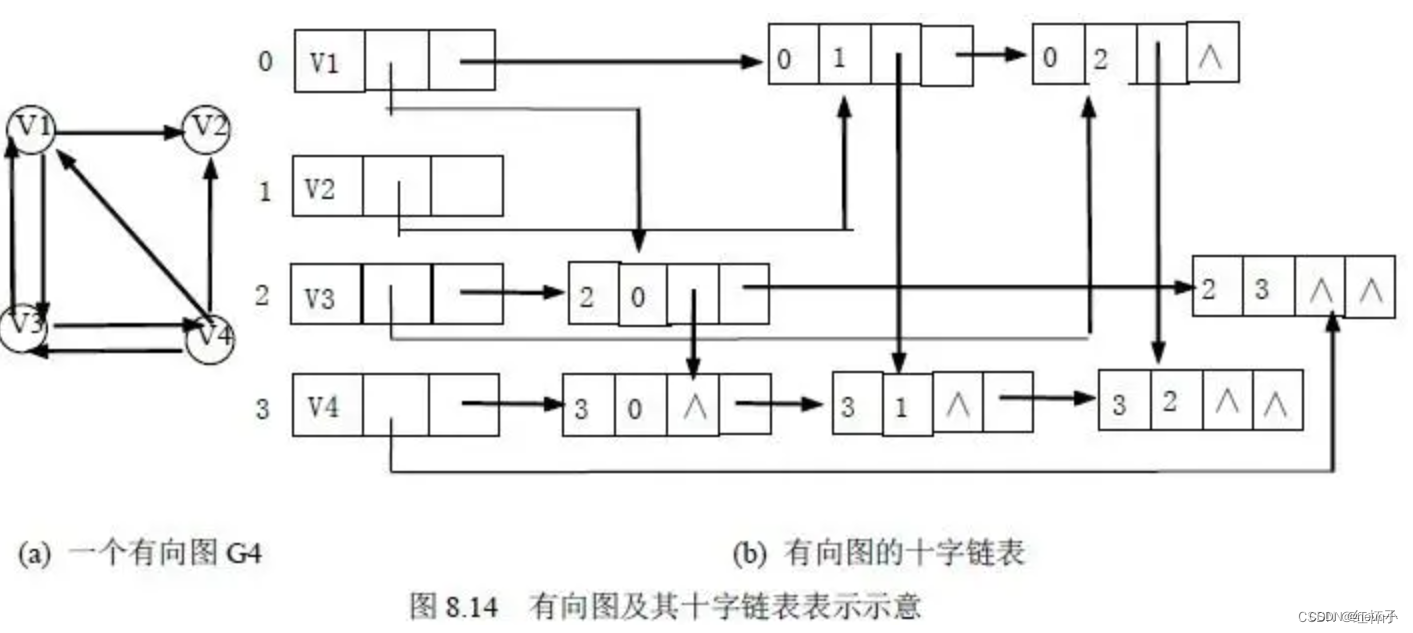
图的十字链表存储结构
1.其实就是邻接表和逆邻接表的结合,说明白点,就是用箭头表示出弧头,弧尾,以及他们之间的关系 2.顶点结构 3.弧结构 3.这样根据上面的结点十字链表结构就很好分析了...

精华回顾:Web3 前沿创新者在 DESTINATION MOON 共话未来
9 月 17 日,由 TinTinLand 主办的「DESTINATION MOON: Web3 Dev Summit Shanghai 2023」线下活动在上海黄浦如约而至。 本次 DESTINATION MOON 活动作为 2023 上海区块链国际周的 Side Event,设立了 4 场主题演讲与 3 个圆桌讨论,聚集了诸多…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
