c++23中的新功能之十五类tuple类型的完全支持
一、std::tuple和std::pair
在传统的C++里一直有一个问题让开发者不爽,就是无法返回多个值。一般来说,返回多个都建议采用封装的模式,比如弄一个结构体或者类啥的。这样做一定时没有问题的,但对于一些只返回一些简单值并且只在偶尔情况下使用的时候儿,封装一个结构体之类的有点用力过猛的意思。
所以在后来出现了std::pair,它其实就是一个类似于封装的一个结体可简化如下:
template<typename T1,typename T2>
struct pair
{T1 first;T2 second;
};
这样一来,就可以在一些需要返回多个值的情况下使用此数据结构。但是这也只是简化了使用而并没有达到其它语言的多值返回,开发者也只能接受。但随着std::tuple的出现,使得std::pair变得有点鸡肋的味道。毕竟这个数据结构虽然说有点方便,但还是有点不方便(比如传三个或者更多的参数)?更让人不好理解的是,泛型的T很难描述first和second的关系,这对于具体到某个公司或者说某个程序来说不算什么大问题,但用在标准库里,可是真得有点问题。
这两个问题的存在,后者在C++20中进行了完善,使用了具名的数据结构体,而前者则是出现了std::tuple。相比std::pair它可以更多的处理异类的参数(当然,同类更没问题),不过它的访问方式相比std::pair有了一些小小的不方便。只能使用类型或索引“std::get(stuTuple) or std::get<0>(stuTuple)”。不过在C++17还提供了聚合初始化访问的方式,类似下面的代码:
auto [a,b,c,d] = getTuple();
std::cout<<a<<b<<c<<d<<std::endl;它等于是简化了使用std::tie来处理这种情况,这样做的好处就不言而喻了。
为了鼓励开发者从std::pair转到std::tuple(std::tuple的应用还真是不多),STL提供了从pair<T,U>到 tuple<T,U>的隐式转换,但反之则不行。这也算是一种诱导法则吧。
二、类tuple类型及处理
在结构化绑定中,理论上讲,只要成员是公有的,都可以直接进行处理。类似于下面的代码:
struct Data{...};
Data d{...};
auto [a,b,c] = d;在C++17中提供了一个std::is_aggregate元编程的接口来判断是否一个可聚合初始化的类型。但是对于一些自定义的非聚合类型呢?这块也有办法。这就是本文提到的类tuple的实现,先看代码:
#include <tuple>
class Data {
private:int id;int num;int value;public:Data(int d, int n, int v) : id{d}, num{n}, value{v} {}int getV() const { return value; }int getN() const { return num; }int getID() const { return id; }
};template <> struct std::tuple_size<Data> : std::integral_constant<int, 3> {};
template <> struct std::tuple_element<0, Data> { using type = int; };
template <> struct std::tuple_element<1, Data> { using type = int; };
template <> struct std::tuple_element<2, Data> { using type = int; };template <int i> auto get(const Data &d) {static_assert(0 <= i && i <= 2);if constexpr (i == 0) {return d.getID();} else if (i == 1) {return d.getN();} else {return d.getV();}
}void testTuple() {Data data{3, 6, 9};auto [id, num, v] = data;
}
说明:
要想实现类tuple类型就需要对下面的三个约束条件进行实现:
1、std::tuple_size_v要符合要求(std::integral_constant<std::size_t, value>),返回一个大于0的长度。
2、std::tuple_element_t<i, T>(i与数组定义类似从0~tuple.size-1)符合要求,其类型要与自定义类型相匹配。
3、必须实现tuple.get或get(tuple),并返回tuple的第i个元素值.
此功能在C++17中已经有所体现,到了C++23有着更强有力的支持:
1、任意标准类tuple类型可以转换成std::tuple,同时能进行大小/相等的比较 ;任意长度为2的标准tuple类型和std::pair可互转,并且可以比较大小/相等
2、任意两个标准类tuple类型之间有common_reference和common_type
3、任意标准类tuple类型现在都能成为tuple_cat/apply/make_from_tuple的参数
这样一来,基本上常见的一些问题都可以解决了。
三、注意点
使用std::tuple和类tuple的人不多,应用场景也不多。但是注意点却很多:
1、尽量使用标准类tuple类型(tuple, pair, array, ranges::subrange),否则会有一些可能想不到意外
2、不要想把tuple相关的函数悉数应用在类tuple类型中
3、尽量使用新标准的编译器
四、总结
人们总是希望新标准能解决问题,但没想到的是,往往新的标准又会引入新的问题。这本身就是一个动态循环的问题,已经是一个众人皆知的现象,但人们仍然还是抱有一种希望吧。不过,新的标准会把一些急切的问题解决并引领开发者不断的向着更好的方向发展,这才是标准发展的意义。
相关文章:

c++23中的新功能之十五类tuple类型的完全支持
一、std::tuple和std::pair 在传统的C里一直有一个问题让开发者不爽,就是无法返回多个值。一般来说,返回多个都建议采用封装的模式,比如弄一个结构体或者类啥的。这样做一定时没有问题的,但对于一些只返回一些简单值并且只在偶尔…...

iPhone15线下购买,苹果零售店前门店排长队
今年的苹果新品发布会于北京时间 9 月 13 日凌晨举行,并于 9 月 15 日(周五)开启订购,9 月 22 日(周五)起正式发售。 据多位网友反馈,首批苹果 iPhone15 系列手机、Apple Watch Ultra 2 / Seri…...

Vue3如何优雅的加载大量图片?
前端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 表妹一键制作自己的五星红旗国庆头像,超好看 最近开发了一个功能,页面首页会加载大量的图片,初次进入页面时ÿ…...
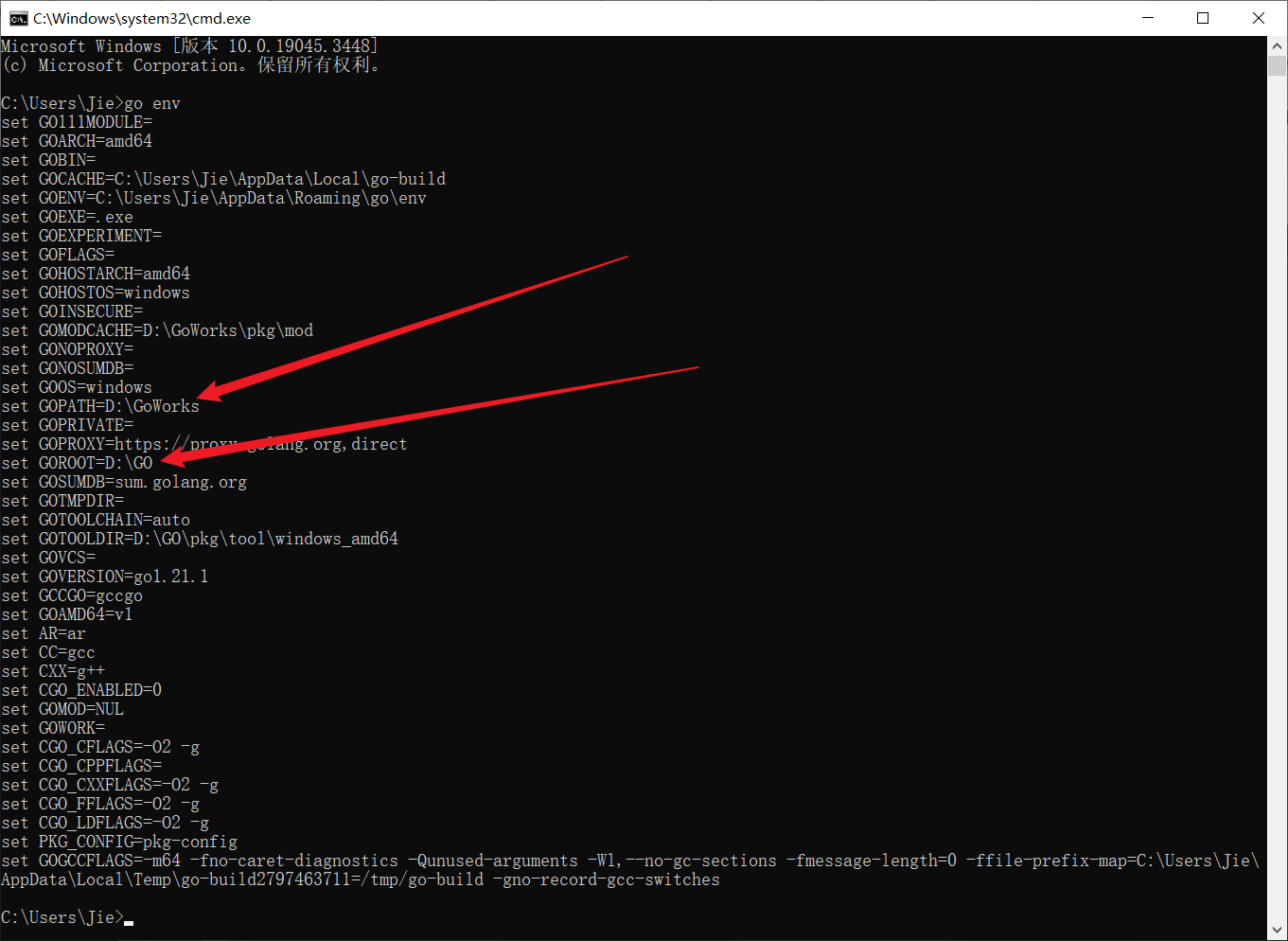
Go语言开发环境搭建指南:快速上手构建高效的Go开发环境
Go 官网:https://go.dev/dl/ Go 语言中文网:https://studygolang.com/dl 下载 Go 的语言包 进入官方网站 Go 官网 或 Go 语言中文网: 选择下载对应操作系统的安装包: 等待下载完成: 安装 Go 的语言包 双击运行上…...
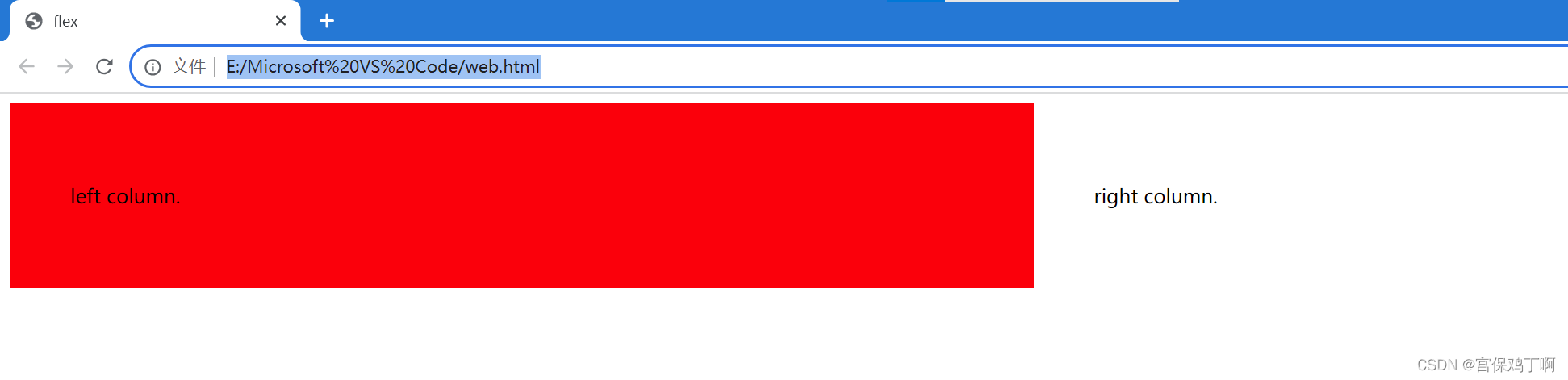
flex布局与float布局
float布局 俩栏 三栏 flex布局...

【C语言】字符函数和字符串函数(含模拟)
前言: 在做OJ题或阅读代码时或多或少会遇到一些字符函数和字符串函数, 如果不认识或不熟悉就会造成不便, 本篇文章主要是为了这方面而存在, 此篇介绍各个字符串的功能与使用方法, 下一篇会讲解如何模拟这些函数 重点&a…...
基于YOLOv8模型的条形码二维码检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOv8模型的条形码二维码检测系统可用于日常生活中检测与定位条形码与二维码目标,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测…...

2023/09/22 制作demo期间心得
A*的估价函数:例如A->C,会计算A到B的距离B到C的距离作为成本,雕刻不会导致全局路线的重新计算,凸多边形是一个内部为凸集的简单多边形。 简单多边形的下列性质与其凸性等价:1、所有内角小于等于180度。 2、任意两个…...
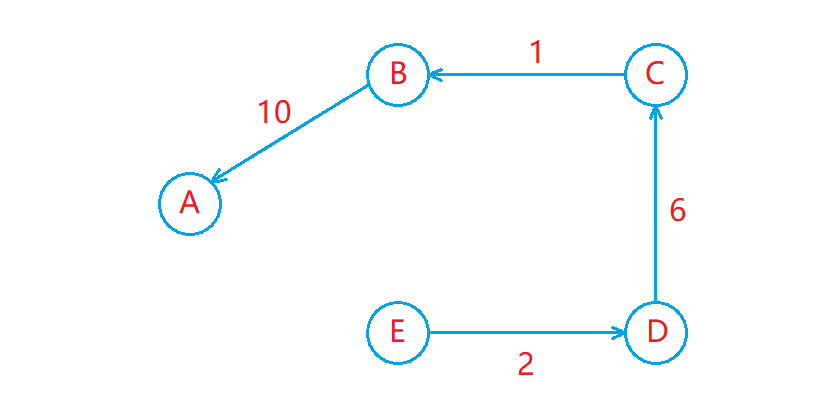
高阶数据结构——图
图 图的基本概念 图的基本概念 图是由顶点集合和边的集合组成的一种数据结构,记作 G ( V , E ) G(V, E)G(V,E) 。 有向图和无向图: 在有向图中,顶点对 < x , y >是有序的,顶点对 < x , y > 称为顶点 x 到顶点 y 的…...

高性能AC算法多关键词匹配文本功能Java实现
直接上测试结果: 1000000数据集。 1000000关键词(匹配词) 装载消耗时间:20869 毫秒 匹配消耗时间:6599 毫秒 代码和测试案例: package com.baian.tggroupmessagematchkeyword.ac;import lombok.Data;im…...
如何在没有第三方.NET库源码的情况,调试第三库代码?
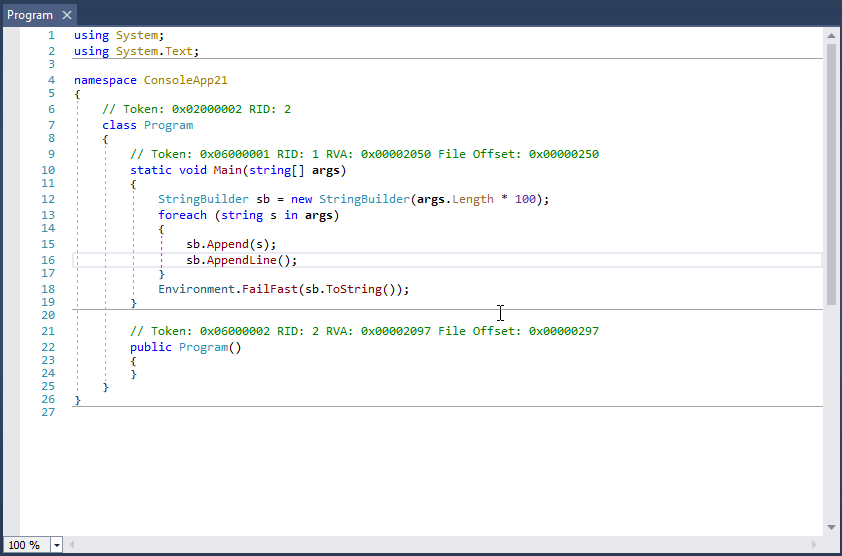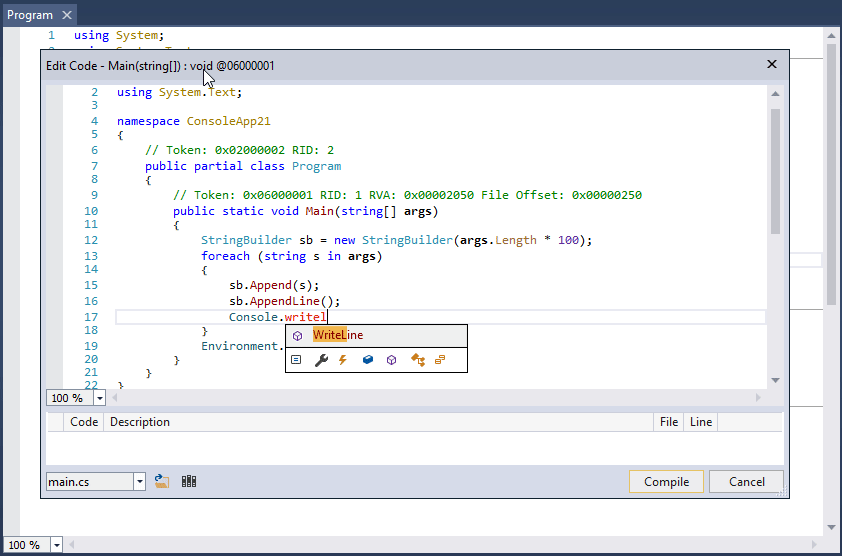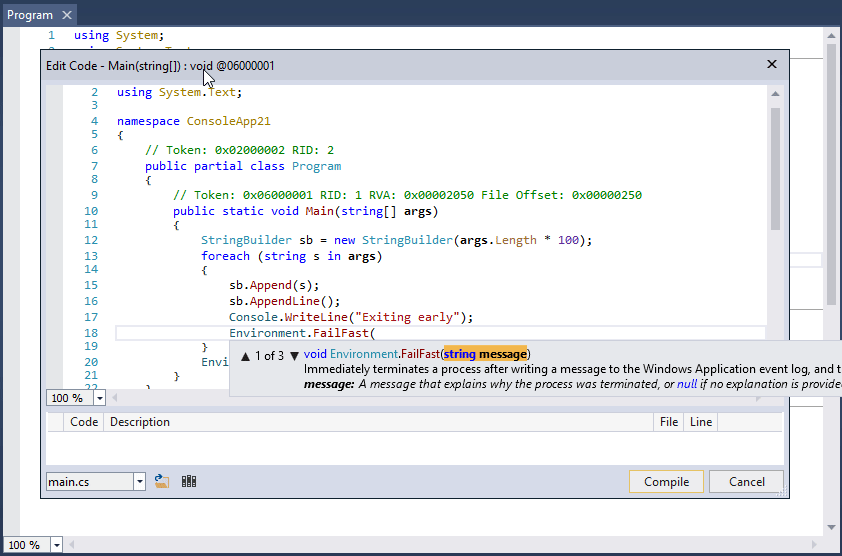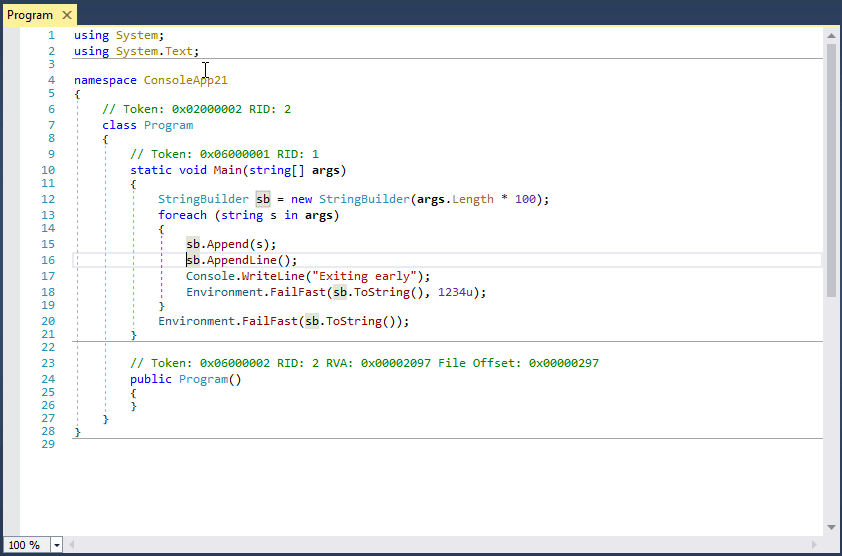
大家好,我是沙漠尽头的狼。 本方首发于Dotnet9,介绍使用dnSpy调试第三方.NET库源码,行文目录: 安装dnSpy编写示例程序调试示例程序调试.NET库原生方法总结 1. 安装dnSpy dnSpy是一款功能强大的.NET程序反编译工具,…...
仿互站资源商城平台系统源码多款应用模版
首先安装好环境,推荐用Linux宝塔 请示:安装前请先别开防火墙,和跨站篡改 第1步上传程序到服务器, 第2步修改数据库文件,config/config.php 第3步,导入数据,根目录的数据库文件夹里面 数据.s…...
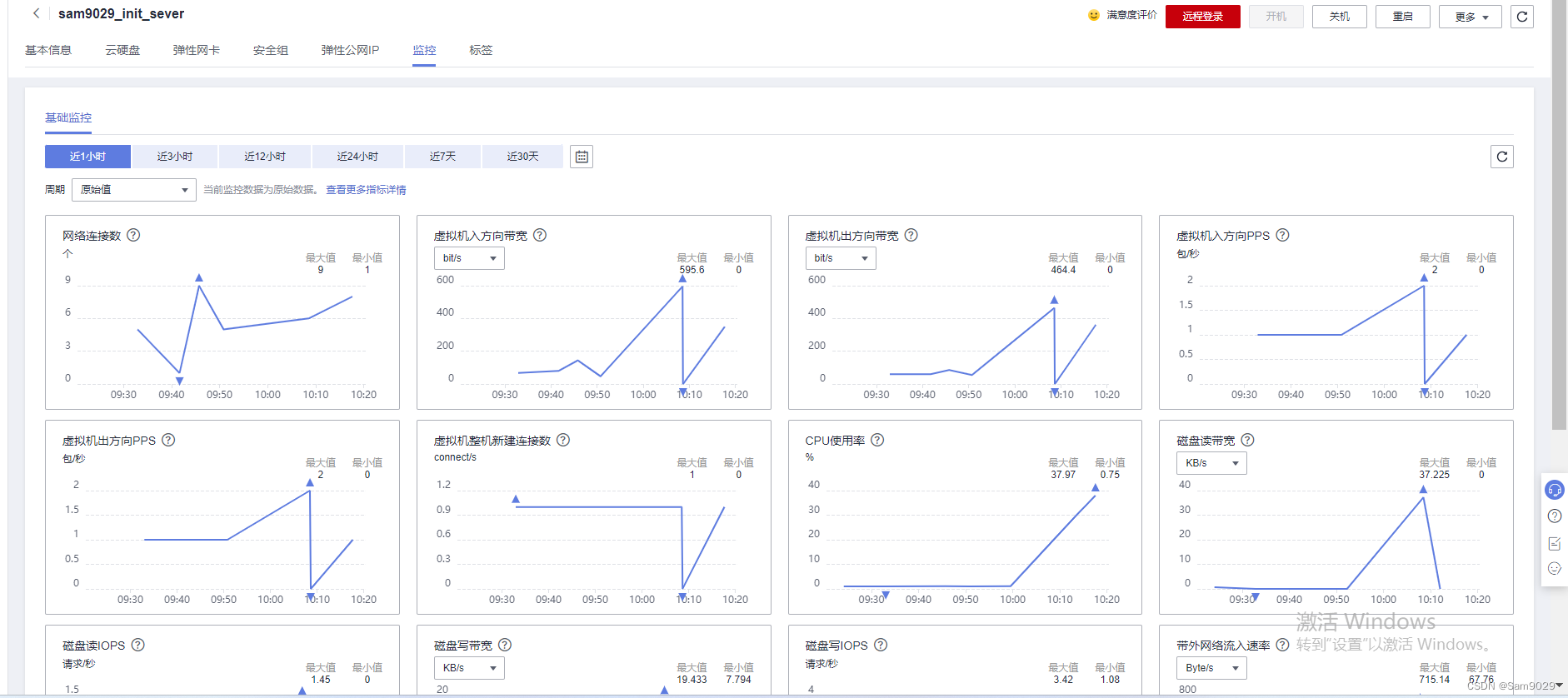
华为云云耀云服务器L实例评测 | L实例性能测试实践
🦖我是Sam9029,一个前端 Sam9029的CSDN博客主页:Sam9029的博客_CSDN博客-JS学习,CSS学习,Vue-2领域博主 **🐱🐉🐱🐉恭喜你,若此文你认为写的不错,不要吝啬你的赞扬,求…...
VR赋能红色教育,让爱国主义精神永放光彩
昨天的918防空警报长鸣,人们默哀,可见爱国主义精神长存。为了贯彻落实“把红色资源利用好、红色传统发扬好、红色基因传承好”的指示精神,许多红色景点开始引入VR全景展示技术,为游客提供全方位720度无死角的景区展示体验。 VR全…...

计算机视觉与深度学习-卷积神经网络-卷积图像去噪边缘提取-图像去噪 [北邮鲁鹏]
目录标题 参考学习链接图像噪声噪声分类椒盐噪声脉冲噪声对椒盐噪声&脉冲噪声去噪使用高斯卷积核中值滤波器 高斯噪声减少高斯噪声 参考学习链接 计算机视觉与深度学习-04-图像去噪&卷积-北邮鲁鹏老师课程笔记 图像噪声 噪声点,其实在视觉上看上去让人感…...

三行代码实现图像画质修复,图片清晰度修复,清晰度提升python
核心代码 # 原始文件 enhancer ImageEnhance.Sharpness(Image.open(文件路径.png)) # 增强图片 img_enhanced enhancer.enhance(增强系数float) # 输出目标文件 img_enhanced.save(文件名.png)注意,输入输出文件格式必须一致 所需依赖 # 文件选择框,…...
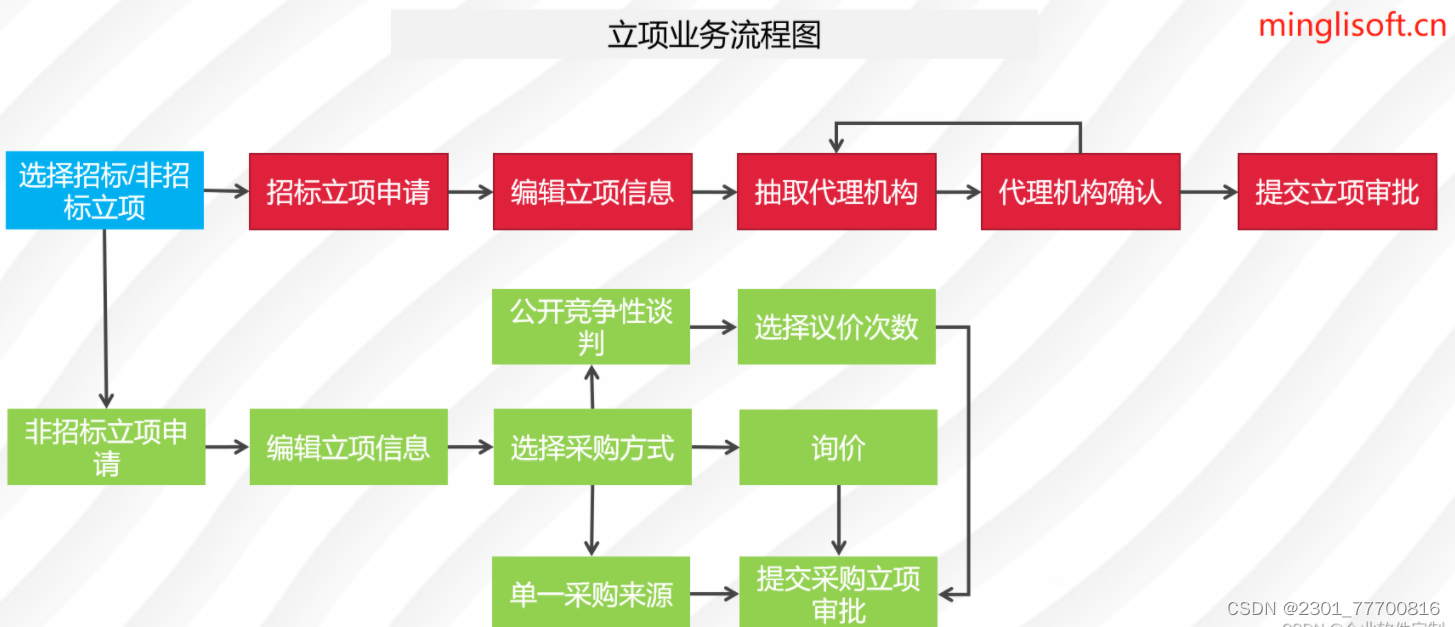
企业电子招投标采购系统源码之电子招投标的组成
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外部供…...
【MySQL】 MySQL的增删改查(进阶)--贰
文章目录 🛫新增🛬查询🌴聚合查询🚩聚合函数🎈GROUP BY子句📌HAVING 🎋联合查询⚾内连接⚽外连接🧭自连接🏀子查询🎡合并查询 🎨MySQL的增删改查(…...

第七章 查找
一、树形查找-二叉排序树和红黑树 二叉排序树 // 二叉排序树节点 typedef struct BSTNode{ElemType key;struct BSTNode *lchild, *rchild; } BSTNode, *BSTree;五叉查找树 // 5叉排序树的节点定义 struct Node{ElemType keys[4]; // 5叉查找树一个节点最多4个关键字struct…...

openfeign返回消息报错.UnknownContentTypeException
1. springcloud项目使用openfeign报错 org.springframework.web.client.UnknownContentTypeException: Could not extract response: no suitable HttpMessageConverter found for response type [com.yl.base.Result<java.util.List<com.yl.entity.LabelConfig>>…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...

信息系统分析与设计复习
2024试卷 单选题(20) 1、在一个聊天系统(类似ChatGPT)中,属于控制类的是()。 A. 话语者类 B.聊天文字输入界面类 C. 聊天主题辨别类 D. 聊天历史类 解析 B-C-E备选架构中分析类分为边界类、控制类和实体类。 边界…...

DL00871-基于深度学习YOLOv11的盲人障碍物目标检测含完整数据集
基于深度学习YOLOv11的盲人障碍物目标检测:开启盲人出行新纪元 在全球范围内,盲人及视觉障碍者的出行问题一直是社会关注的重点。尽管技术不断进步,许多城市的无障碍设施依然未能满足盲人出行的实际需求。尤其是在复杂的城市环境中ÿ…...
