极坐标和直角坐标的雅克比矩阵推导
我们经常需要在一些问题中研究坐标系的关系,这里讲讲最常见的极坐标和直角坐标的雅克比矩阵的推导。以二维坐标为例,三维坐标也是同理。
1. 直角坐标和极坐标
直角坐标表示为 ( x , y ) (x,y) (x,y),极坐标表示为 ( ρ , φ ) (\rho,\varphi) (ρ,φ),它们之间有如下的关系:
ρ 2 = x 2 + y 2 , φ = arctan y x ; x = ρ cos φ , y = ρ sin φ \begin{aligned} \rho^2=x^2+y^2,\quad &\varphi=\arctan\frac{y}{x};\\ x=\rho\cos\varphi,\quad&y=\rho\sin\varphi \end{aligned} ρ2=x2+y2,x=ρcosφ,φ=arctanxy;y=ρsinφ
2. 向量之间的雅克比矩阵
向量X和向量Y的微分映射由雅克比矩阵来刻画,给定两个向量 x = ( x 1 , x 2 , ⋯ , x n ) T \mathbf{x}=(x_1,x_2,\cdots,x_n)^T x=(x1,x2,⋯,xn)T, y = ( y 1 , y 2 , ⋯ , y m ) T \mathbf{y}=(y_1,y_2,\cdots,y_m)^T y=(y1,y2,⋯,ym)T
{ d x 1 = ∂ x 1 ∂ y 1 d y 1 + ∂ x 1 ∂ y 2 d y 2 + ⋯ + ∂ x 1 ∂ y m d y m d x 2 = ∂ x 2 ∂ y 1 d y 1 + ∂ x 2 ∂ y 2 d y 2 + ⋯ + ∂ x 2 ∂ y m d y m ⋮ d x n = ∂ x n ∂ y 1 d y 1 + ∂ x n ∂ y 2 d y 2 + ⋯ + ∂ x n ∂ y m d y m \begin{aligned} \begin{cases} \mathrm{d}x_1=\dfrac{\partial x_1}{\partial y_1}\mathrm{d}y_1+\dfrac{\partial x_1}{\partial y_2}\mathrm{d}y_2+\cdots+\dfrac{\partial x_1}{\partial y_m}\mathrm{d}y_m\\ \mathrm{d}x_2=\dfrac{\partial x_2}{\partial y_1}\mathrm{d}y_1+\dfrac{\partial x_2}{\partial y_2}\mathrm{d}y_2+\cdots+\dfrac{\partial x_2}{\partial y_m}\mathrm{d}y_m\\ \vdots\\ \mathrm{d}x_n=\dfrac{\partial x_n}{\partial y_1}\mathrm{d}y_1+\dfrac{\partial x_n}{\partial y_2}\mathrm{d}y_2+\cdots+\dfrac{\partial x_n}{\partial y_m}\mathrm{d}y_m\\ \end{cases} \end{aligned} ⎩ ⎨ ⎧dx1=∂y1∂x1dy1+∂y2∂x1dy2+⋯+∂ym∂x1dymdx2=∂y1∂x2dy1+∂y2∂x2dy2+⋯+∂ym∂x2dym⋮dxn=∂y1∂xndy1+∂y2∂xndy2+⋯+∂ym∂xndym
写成矩阵的形式就是:
( d x 1 d x 2 ⋮ d x n ) = [ ∂ x 1 ∂ y 1 ∂ x 1 ∂ y 2 ⋯ ∂ x 1 ∂ y m ∂ x 2 ∂ y 1 ∂ x 2 ∂ y 2 ⋯ ∂ x 2 ∂ y m ⋮ ⋮ ⋮ ∂ x n ∂ y 1 ∂ x n ∂ y 2 ⋯ ∂ x n ∂ y m ] ( d y 1 d y 2 ⋮ d y m ) \begin{pmatrix} \mathrm{d}x_1\\ \mathrm{d}x_2\\ \vdots\\ \mathrm{d}x_n \end{pmatrix} =\begin{bmatrix} \dfrac{\partial x_1}{\partial y_1} & \dfrac{\partial x_1}{\partial y_2} & \cdots & \dfrac{\partial x_1}{\partial y_m}\\ \dfrac{\partial x_2}{\partial y_1} & \dfrac{\partial x_2}{\partial y_2} & \cdots &\dfrac{\partial x_2}{\partial y_m} \\ \vdots & \vdots & & \vdots\\ \dfrac{\partial x_n}{\partial y_1} & \dfrac{\partial x_n}{\partial y_2} & \cdots &\dfrac{\partial x_n}{\partial y_m} \end{bmatrix}\begin{pmatrix} \mathrm{d}y_1\\ \mathrm{d}y_2\\ \vdots\\ \mathrm{d}y_m \end{pmatrix} dx1dx2⋮dxn = ∂y1∂x1∂y1∂x2⋮∂y1∂xn∂y2∂x1∂y2∂x2⋮∂y2∂xn⋯⋯⋯∂ym∂x1∂ym∂x2⋮∂ym∂xn dy1dy2⋮dym
其中的矩阵
∂ ( x 1 , x 2 , ⋯ , x n ) ∂ ( y 1 , y 2 , ⋯ , y m ) = [ ∂ x 1 ∂ y 1 ∂ x 1 ∂ y 2 ⋯ ∂ x 1 ∂ y m ∂ x 2 ∂ y 1 ∂ x 2 ∂ y 2 ⋯ ∂ x 2 ∂ y m ⋮ ⋮ ⋮ ∂ x n ∂ y 1 ∂ x n ∂ y 2 ⋯ ∂ x n ∂ y m ] \frac{\partial(x_1,x_2,\cdots,x_n)}{\partial(y_1,y_2,\cdots,y_m)}=\begin{bmatrix} \dfrac{\partial x_1}{\partial y_1} & \dfrac{\partial x_1}{\partial y_2} & \cdots & \dfrac{\partial x_1}{\partial y_m}\\ \dfrac{\partial x_2}{\partial y_1} & \dfrac{\partial x_2}{\partial y_2} & \cdots &\dfrac{\partial x_2}{\partial y_m} \\ \vdots & \vdots & & \vdots\\ \dfrac{\partial x_n}{\partial y_1} & \dfrac{\partial x_n}{\partial y_2} & \cdots &\dfrac{\partial x_n}{\partial y_m} \end{bmatrix} ∂(y1,y2,⋯,ym)∂(x1,x2,⋯,xn)= ∂y1∂x1∂y1∂x2⋮∂y1∂xn∂y2∂x1∂y2∂x2⋮∂y2∂xn⋯⋯⋯∂ym∂x1∂ym∂x2⋮∂ym∂xn
就是雅克比矩阵。我们称从坐标 y \mathbf{y} y(分母)到 x \mathbf{x} x(分子)的雅克比矩阵。
3. 极坐标到直角坐标的雅克比矩阵
这个比较简单,利用关系 x = ρ cos φ , y = ρ sin φ x=\rho\cos\varphi,y=\rho\sin\varphi x=ρcosφ,y=ρsinφ,
∂ x ∂ ρ = cos φ , ∂ x ∂ φ = − ρ sin φ ∂ y ∂ ρ = sin φ , ∂ y ∂ φ = ρ cos φ \begin{aligned} \dfrac{\partial x}{\partial \rho}=\cos\varphi, & \dfrac{\partial x}{\partial \varphi}=-\rho\sin\varphi\\ \dfrac{\partial y}{\partial \rho}=\sin\varphi, &\dfrac{\partial y}{\partial \varphi}=\rho\cos\varphi \end{aligned} ∂ρ∂x=cosφ,∂ρ∂y=sinφ,∂φ∂x=−ρsinφ∂φ∂y=ρcosφ
我们可以写出雅克比矩阵
∂ ( x , y ) ∂ ( ρ , φ ) = [ ∂ x ∂ ρ ∂ x ∂ φ ∂ y ∂ ρ ∂ y ∂ φ ] = [ cos φ − ρ sin φ sin φ ρ cos φ ] \dfrac{\partial(x,y)}{\partial(\rho,\varphi)}=\begin{bmatrix} \dfrac{\partial x}{\partial \rho} & \dfrac{\partial x}{\partial \varphi}\\ \dfrac{\partial y}{\partial \rho} &\dfrac{\partial y}{\partial \varphi} \end{bmatrix}=\begin{bmatrix} \cos\varphi &-\rho\sin\varphi\\ \sin\varphi &\rho\cos\varphi \end{bmatrix} ∂(ρ,φ)∂(x,y)= ∂ρ∂x∂ρ∂y∂φ∂x∂φ∂y =[cosφsinφ−ρsinφρcosφ]
4. 直角坐标到极坐标的雅克比矩阵
这里有两种方法。
4.1 直接求解
利用关系 ρ 2 = x 2 + y 2 , φ = arctan y x \rho^2=x^2+y^2,\quad \varphi=\arctan\frac{y}{x} ρ2=x2+y2,φ=arctanxy,我们可以对上式直接应用求导
对于第一个式子: ρ = x 2 + y 2 \rho=\sqrt{x^2+y^2} ρ=x2+y2
直接求导有:
∂ ρ ∂ x = 2 x 2 x 2 + y 2 = x ρ = cos φ ∂ ρ ∂ y = 2 y 2 x 2 + y 2 = y ρ = sin φ \frac{\partial\rho}{\partial x}=\frac{2x}{2\sqrt{x^2+y^2}}=\frac{x}{\rho}=\cos\varphi\\ \frac{\partial\rho}{\partial y}=\frac{2y}{2\sqrt{x^2+y^2}}=\frac{y}{\rho}=\sin\varphi ∂x∂ρ=2x2+y22x=ρx=cosφ∂y∂ρ=2x2+y22y=ρy=sinφ
对于第二个式子直接求导有:
∂ φ ∂ x = − y x 2 1 + y 2 x 2 = − y x 2 + y 2 = − y ρ 2 = − sin φ ρ ∂ φ ∂ y = 1 x 1 + y 2 x 2 = x x 2 + y 2 = x ρ 2 = cos φ ρ \frac{\partial \varphi}{\partial x}=\frac{-\dfrac{y}{x^{2}}}{1+\dfrac{y^{2}}{x^{2}}}=\frac{-y}{x^{2}+y^{2}}=\frac{-y}{\rho^2}=\frac{-\sin\varphi}{\rho}\\ \frac{\partial \varphi}{\partial y}=\frac{\dfrac{1}{x}}{1+\dfrac{y^{2}}{x^{2}}}=\frac{x}{x^{2}+y^{2}}=\frac{x}{\rho^2}=\frac{\cos\varphi}{\rho} ∂x∂φ=1+x2y2−x2y=x2+y2−y=ρ2−y=ρ−sinφ∂y∂φ=1+x2y2x1=x2+y2x=ρ2x=ρcosφ
当然也可以用全微分的方法来求解,我们对第一个式子全微分:
2 ρ d ρ = 2 x d x + 2 y d y 2\rho\mathrm{d}\rho=2x\mathrm{d}x+2y\mathrm{d}y 2ρdρ=2xdx+2ydy
于是得到
d ρ = x ρ d x + y ρ d y \mathrm{d}\rho=\frac{x}{\rho}\mathrm{d}x+\frac{y}{\rho}\mathrm{d}y dρ=ρxdx+ρydy
于是有:
∂ ρ ∂ x = x ρ = cos φ , ∂ y ∂ ρ = y ρ = sin φ \dfrac{\partial \rho}{\partial x}=\frac{x}{\rho}=\cos\varphi, \dfrac{\partial y}{\partial \rho}=\frac{y}{\rho}=\sin\varphi ∂x∂ρ=ρx=cosφ,∂ρ∂y=ρy=sinφ
对第二个式子变换一下:
tan φ = y x \tan\varphi=\frac{y}{x} tanφ=xy
然后我们再求全微分:
1 cos 2 φ d φ = − y x 2 d x + 1 x d y \frac{1}{\cos^2\varphi}\mathrm{d}\varphi=-\frac{y}{x^2}\mathrm{d}x+\frac{1}{x}\mathrm{d}y cos2φ1dφ=−x2ydx+x1dy
于是得到
d φ = − y cos 2 φ x 2 d x + cos 2 φ x d y = − y ρ 2 d x + x ρ 2 d y = − sin φ ρ d x + cos φ ρ d y \mathrm{d}\varphi=-\frac{y\cos^2\varphi}{x^2}\mathrm{d}x+\frac{\cos^2\varphi}{x}\mathrm{d}y=-\frac{y}{\rho^2}\mathrm{d}x+\frac{x}{\rho^2}\mathrm{d}y=-\frac{\sin\varphi}{\rho}\mathrm{d}x+\frac{\cos\varphi}{\rho}\mathrm{d}y dφ=−x2ycos2φdx+xcos2φdy=−ρ2ydx+ρ2xdy=−ρsinφdx+ρcosφdy
于是有:
∂ φ ∂ x = − sin φ ρ , ∂ φ ∂ y = cos φ ρ \frac{\partial \varphi}{\partial x}=\frac{-\sin\varphi}{\rho}, \frac{\partial \varphi}{\partial y}=\frac{\cos\varphi}{\rho} ∂x∂φ=ρ−sinφ,∂y∂φ=ρcosφ
∂ ( ρ , φ ) ∂ ( x , y ) = [ ∂ ρ ∂ x ∂ ρ ∂ y ∂ φ ∂ x ∂ φ ∂ y ] = [ cos φ sin φ − sin φ ρ cos φ ρ ] \dfrac{\partial(\rho,\varphi)}{\partial(x,y)}=\begin{bmatrix} \dfrac{\partial \rho}{\partial x} & \dfrac{\partial \rho}{\partial y}\\ \dfrac{\partial \varphi}{\partial x}&\dfrac{\partial \varphi}{\partial y} \end{bmatrix}=\begin{bmatrix} \cos\varphi &\sin\varphi\\ \dfrac{-\sin\varphi}{\rho}&\dfrac{\cos\varphi}{\rho} \end{bmatrix} ∂(x,y)∂(ρ,φ)= ∂x∂ρ∂x∂φ∂y∂ρ∂y∂φ = cosφρ−sinφsinφρcosφ
4.2 求逆
这里刚好是一个二阶方阵,所以可以直接对3中的雅克比矩阵求逆:
∂ ( ρ , φ ) ∂ ( x , y ) = ( ∂ ( x , y ) ∂ ( ρ , φ ) ) − 1 = [ cos φ − ρ sin φ sin φ ρ cos φ ] − 1 = [ cos φ sin φ − sin φ ρ cos φ ρ ] \dfrac{\partial(\rho,\varphi)}{\partial(x,y)}=\left(\dfrac{\partial(x,y)}{\partial(\rho,\varphi)}\right)^{-1}=\begin{bmatrix} \cos\varphi &-\rho\sin\varphi\\ \sin\varphi &\rho\cos\varphi \end{bmatrix}^{-1}{}=\begin{bmatrix} \cos\varphi &\sin\varphi\\ \dfrac{-\sin\varphi}{\rho}&\dfrac{\cos\varphi}{\rho} \end{bmatrix} ∂(x,y)∂(ρ,φ)=(∂(ρ,φ)∂(x,y))−1=[cosφsinφ−ρsinφρcosφ]−1= cosφρ−sinφsinφρcosφ
相关文章:

极坐标和直角坐标的雅克比矩阵推导
我们经常需要在一些问题中研究坐标系的关系,这里讲讲最常见的极坐标和直角坐标的雅克比矩阵的推导。以二维坐标为例,三维坐标也是同理。 1. 直角坐标和极坐标 直角坐标表示为 ( x , y ) (x,y) (x,y),极坐标表示为 ( ρ , φ ) (\rho,\varph…...

经管博士科研基础【25】概率论中的相关基础概念
1. Support 在概率论中,"support"(支撑集)是指随机变量可能取值的集合。对于离散型随机变量,支撑集包含了所有可能的取值;而对于连续型随机变量,支撑集是指其密度函数或概率质量函数非零的区域。…...
)
计算机网络的相关知识点总结(一)
1.谈一谈对OSI七层模型和TCP/IP四层模型的理解? 不管是OSI七层模型亦或是TCP/IP四层模型,它们的提出都有一个共同的目的:通过分层来将复杂问题细化,通过各个层级之间的相互配合来更好的解决计算机中出现的问题。 说到分层…...
下载github.com上的依赖资源
下载github.com上的依赖资源(需要反复试才能成功,所以单独安装) export GIT_TRACE1 export GIT_CURL_VERBOSE1 pip install githttps://github.com/PanQiWei/AutoGPTQ.git -i https://pypi.mirrors.ustc.edu.cn/simple --trusted-hostpypi.mi…...

编写 GPT 提示词的公式 + 资源分享
GPT 能够给我们带来很大的帮助,因此我们要好好利用它。我们希望 GPT 输出令我们满意的内容,影响 GPT 输出内容的因素有模型和输入(Prompt,提示词)。 模型:我们可以选择不同的 GPT 产品,它们的模…...
用HTML、CSS和JavaScript制作的通用进制转换器
随着编程和计算机科学越来越受欢迎,我们经常需要进行进制转换。本文将介绍一个简洁、美观、适用于移动设备的进制转换工具,并详细讨论其实现。 目录 🌍 用HTML、CSS和JavaScript制作的通用进制转换器 1.项目图片展示 2. 技术栈 3. 主要功…...
ArcGIS 10.3软件安装包下载及安装教程!
【软件名称】:ArcGIS 10.3 【安装环境】:Windows 【下载链接 】: 链接:https://pan.baidu.com/s/1K5ab7IHMYa23HpmuPkFa1A 提取码:oxbb 复制这段内容后打开百度网盘手机App,操作更方便哦 软件解压码点击原文…...

【数据增强】
【数据增强】 1 数据增强的情形2 数据增强的方法 1 数据增强的情形 当数据比较小,难以获取新的训练数据时,可以考虑数据增强,如随机裁剪部分,随机左右上下翻转、随机旋转一个角度、随机亮度变化等微小变化,数据的多样…...

Ae 效果:CC Force Motion Blur
时间/CC Force Motion Blur Time/CC Force Motion Blur CC Force Motion Blur (CC 强制运动模糊)主要用于为动态图像添加强制的运动模糊效果,增加动态画面的流畅感和真实感。 相对于时间轴面板上的“运动模糊”开关,CC Force Moti…...

2023华为杯研究生数学建模竞赛CDEF题思路+模型代码
全程更新华为杯研赛CDEF题思路模型及代码,大家查看文末名片获取 华为杯C题思路分析 问题一 在每个评审阶段,作品通常都是随机分发的,每份作品需要多位评委独立评审。为了增加不同评审专家所给成绩之间的可比性,不同专家评审的作…...

FP独立站之黑科技:AB站收款、斗篷CLOAK
最近一段时间经常有不少小伙伴来咨询我独立站的相关的业务,因为很多独立站卖家觉得独立站不好做,再加上跨境平台禁止特货类产品的销售(如FP产品、成人用品、电子烟、灰黑类产品等等),但这类产品市场需求大,…...
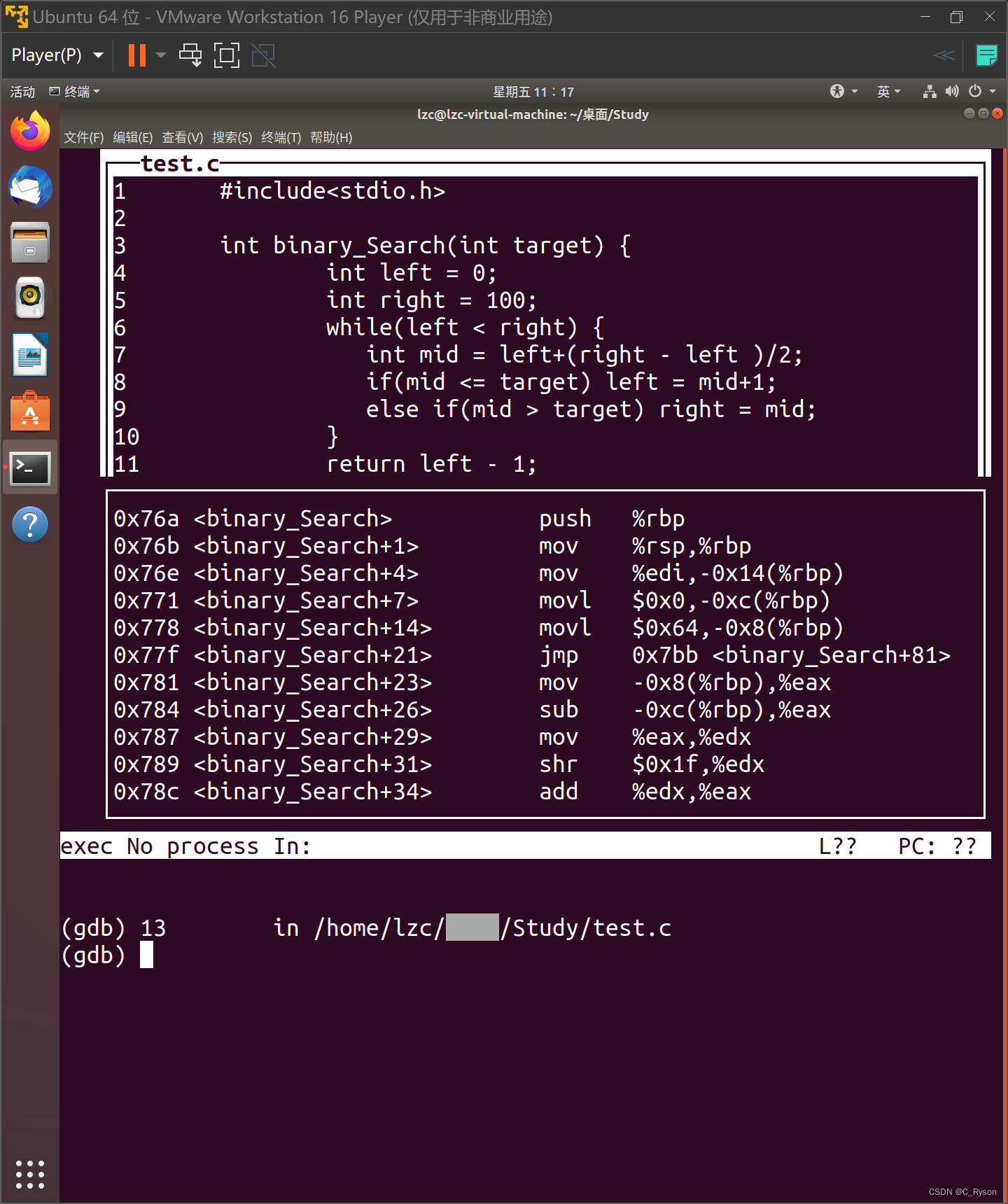
【Linux网络编程】gdb调试技巧
这篇博客主要要记录一下自己在Linux操作系统Ubuntu下使用gbd调试程序的一些指令,以及使用过程中的一些心得。 使用方法 可以使用如下代码 gcc -g test.c -o test 或者 gcc test.c -o test -g的选项最好添加,如果不添加,l指令无法被识别 …...
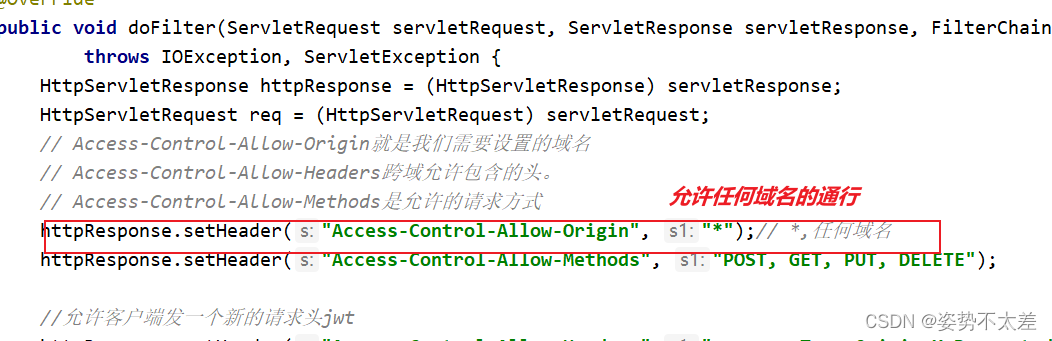
ElementUI之登录与注册
目录 一.前言 二.ElementUI的简介 三.登录注册前端界面的开发 三.vue axios前后端交互--- Get请求 四.vue axios前后端交互--- Post请求 五.跨域问题 一.前言 这一篇的知识点在前面两篇的博客中就已经详细详解啦,包括如何环境搭建和如何建一个spa项目等等知识…...

报错处理:Error: Redis server is running but Redis CLI cannot connect
嗨,读者朋友们!今天我来跟大家分享一个我在运维过程中遇到的一个关于Linux上运行Redis服务时的报错及解决方法。 报错信息如下: Error: Redis server is running but Redis CLI cannot connect 这个报错信息表明Redis服务器已经运行ÿ…...

RocketMQ 源码分析——Producer
文章目录 消息发送代码实现消息发送者启动流程检查配置获得MQ客户端实例启动实例定时任务 Producer 消息发送流程选择队列默认选择队列策略故障延迟机制策略*两种策略的选择 技术亮点:ThreadLocal 消息发送代码实现 下面是一个生产者发送消息的demo(同步发送&#…...

ISTQB术语表
此术语表为国际软件测试认证委员会(ISTQB)发布的标准术语表。此表历经数次修改、完善,集纳了计算机行业界、商业界及政府相关机构的见解及意见,在国际化的层面上达到了罕有的统一性及一致性。参与编制此表的国际团体包括澳大利亚、…...
小米笔试题——01背包问题变种
这段代码的主要思路是使用动态规划来构建一个二维数组 dp,其中 dp[i][j] 表示前 i 个产品是否可以组合出金额 j。通过遍历产品列表和可能的目标金额,不断更新 dp 数组中的值,最终返回 dp[N][M] 来判断是否可以组合出目标金额 M。如果 dp[N][M…...

SkyWalking内置MQE语法
此文档出自SkyWalking官方git https://github.com/apache/skywalking docs/en/api/metrics-query-expression.md Metrics Query Expression(MQE) Syntax MQE is a string that consists of one or more expressions. Each expression could be a combination of one or more …...
Springboot2 Pandas Pyecharts 量子科技专利课程设计大作业
数据集介绍 1.背景 根据《中国科学:信息科学》期刊上的一篇文章,量子通信包括多种协议与应用类型: 基于量子隐形传态与量子存储中继等技术,可实现量子态信息传输,进而构建量子信息网络,已成为当前科研热点&…...

RabbitMQ里的几个重要概念
RabbitMQ中的一些角色: publisher:生产者consumer:消费者exchange个:交换机,负责消息路由,接受生产者发送的消息,把消息发送到一个或多个队列里queue:队列,存储消息virt…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
