浮点数在内存中的存储——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是浮点数在内存中的存储,昨天我们已经写过了整型在内存中的存储,那么,浮点数在内存中是怎样存储的呢?现在,就让我们进入浮点数在内存中的存储的世界吧
常见的浮点数:
3.14159
1E10
浮点数家族包括: float、double、long double 类型。
浮点数表示的范围:float.h中定义
整型家族的类型的取值范围:limit.h
下面,我们来看一小段代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}
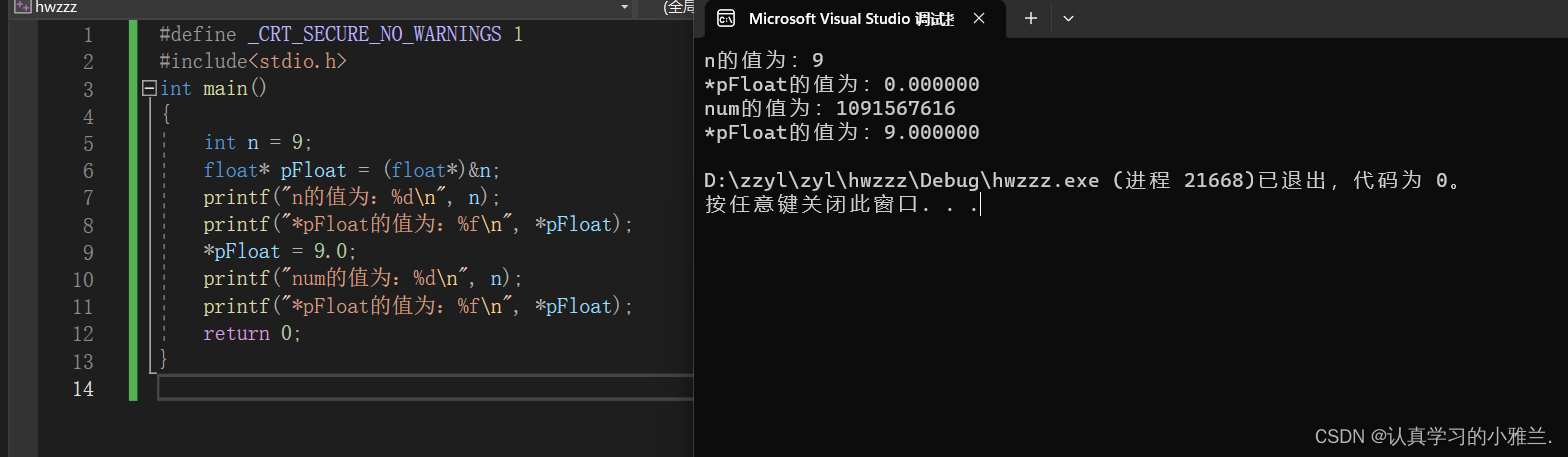
仔细一想:打印出来的结果为什么会是这个样子呢?
浮点数存储规则
num 和 *pFloat 在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?
要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法。
详细解读: 根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^S * M * 2^E
- (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
- M表示有效数字,大于等于1,小于2。
- 2^E表示指数位。


十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754规定:
对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。

IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过, 1≤M,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分。
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时 候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位, 将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int),这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间 数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
举个例子:
#include<stdio.h>
int main()
{float f = 5.5f;//101.1//(-1)^0*1.011*2^2//0 10000001 01100000000000000000000// 2+127//把二进制转化为十六进制//40b00000return 0;
}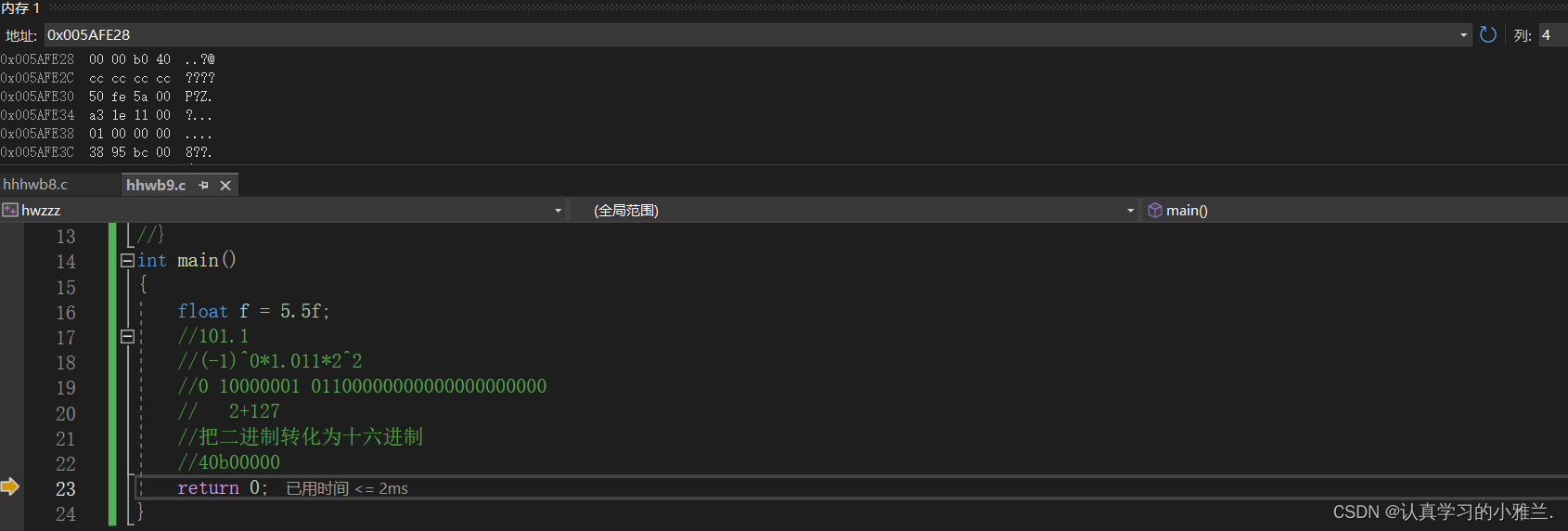
可见,事实就是如此!
然后,指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将 有效数字M前加上第一位的1。
比如:0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2^(-1),其阶码为-1+127=126,表示01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:
0 01111110 00000000000000000000000
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
1.××× * 2^-127
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)
1.××× * 2^128
好了,关于浮点数的表示规则,就说到这里。
那么,之前的那个我们不理解的打印结果就说得通了
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}
int n = 9;
float* pFloat = (float*)&n;
00000000000000000000000000001001 —— 9的原码
00000000000000000000000000001001 —— 9的反码
00000000000000000000000000001001 —— 9的补码
0 00000000 00000000000000000001001
E=1-127=-126
M=0.00000000000000000001001
(-1)^0*0.00000000000000000001001*2^-126
显然,V是一个很小的接近于0的正数,所以用十进制小数表示就是0.000000。
*pFloat = 9.0;
1001.0
1.001*2^3
(-1)^0*1.001*2^3
S=0
M=1.001
E=3
第一位的符号位S=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130, 即10000010。
0 10000010 00100000000000000000000
3+127
这个32位的二进制数,还原成十进制,正是 1091567616 。
好啦,小雅兰今天的内容就到这里啦,还要继续加油呀!!!

相关文章:

浮点数在内存中的存储——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是浮点数在内存中的存储,昨天我们已经写过了整型在内存中的存储,那么,浮点数在内存中是怎样存储的呢?现在,就让我们进入浮点数在内存中的存储的世界吧…...

华为OD机试 C++ 实现 - 租车骑绿岛
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
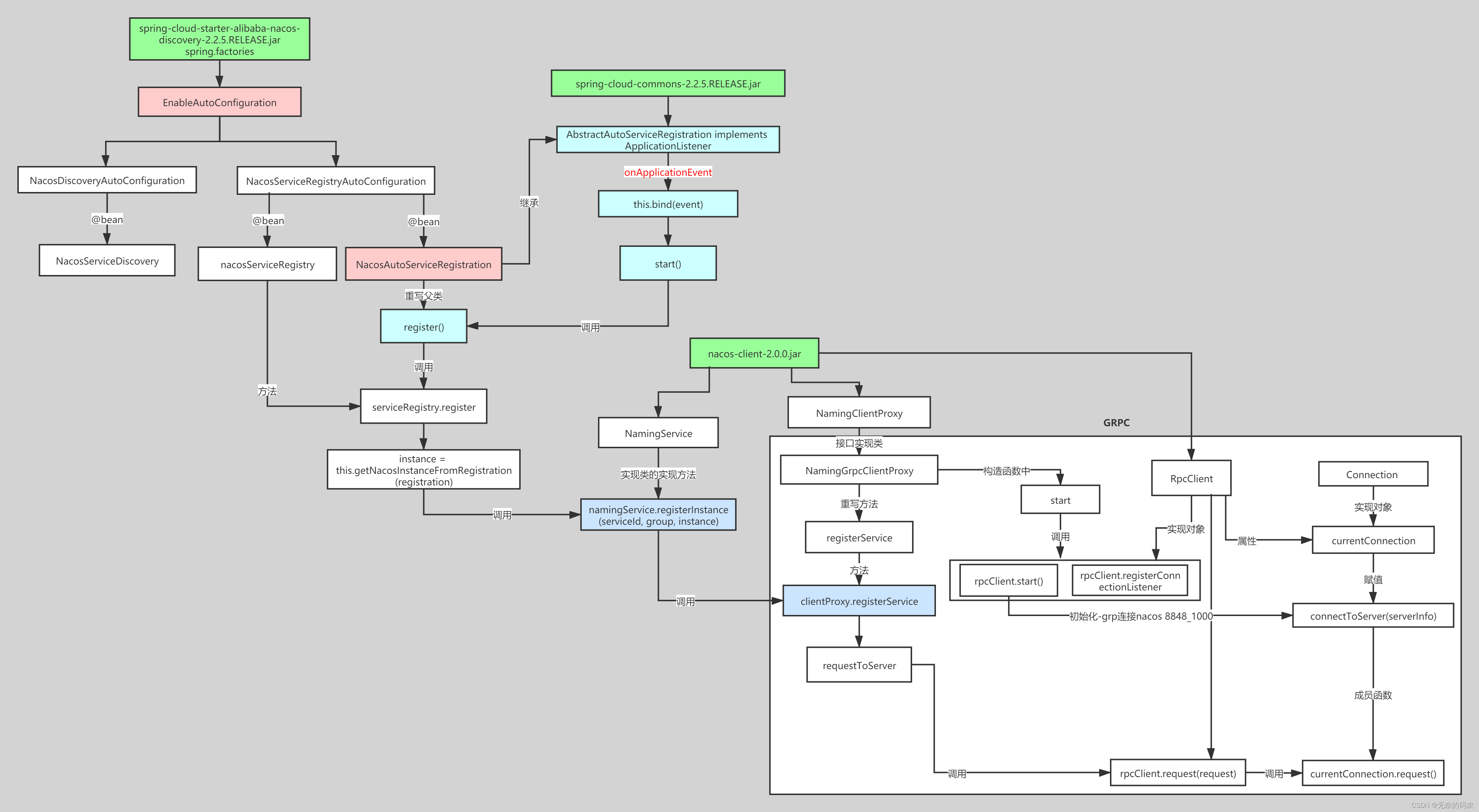
Spring Cloud Nacos源码讲解(三)- Nacos客户端实例注册源码分析
Nacos客户端实例注册源码分析 实例客户端注册入口 流程图: 实际上我们在真实的生产环境中,我们要让某一个服务注册到Nacos中,我们首先要引入一个依赖: <dependency><groupId>com.alibaba.cloud</groupId><…...

位运算(C/C++)
1. 基础知识 程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如,and运算本来是一个逻辑运算符,但整数与整数之间也可以进行and运算。举个例子,6的二进制是110,11的二…...

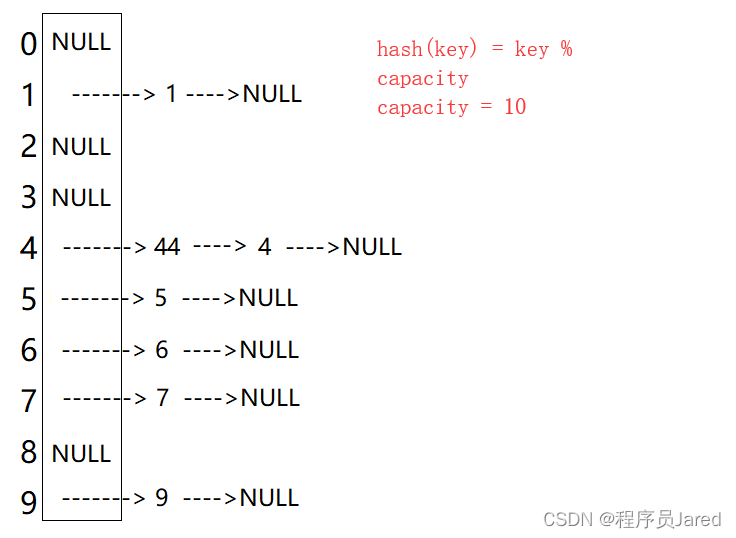
哈希表题目:设计哈希映射
文章目录题目标题和出处难度题目描述要求示例数据范围前言解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:设计哈希映射 出处:706. 设计哈希映射 难度 3 级 题目描述 要求 不使用任何内建的哈希表库设计一个…...

力扣解法汇总1238. 循环码排列
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接: 力扣 描述: 给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,,...,2^n-1) 的排列 p&…...
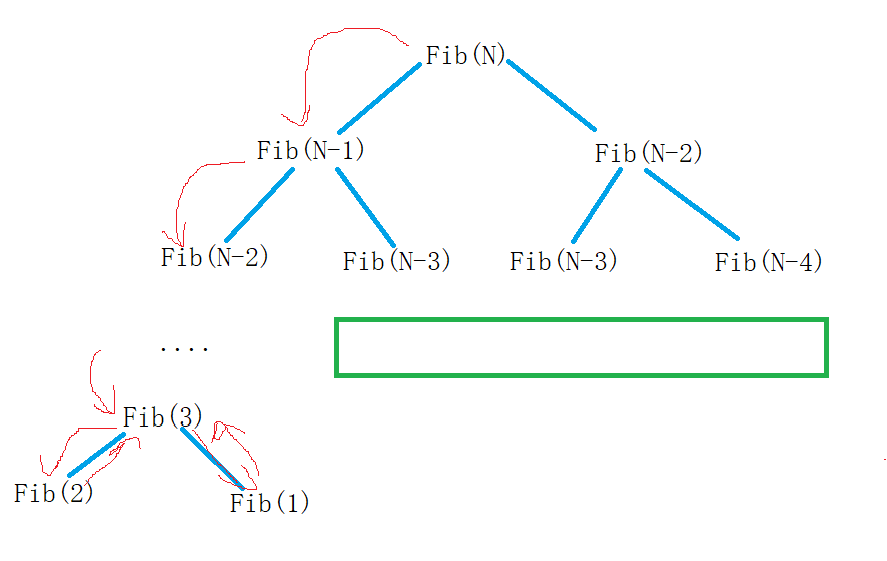
[数据结构]时间复杂度与空间复杂度
[数据结构]时间复杂度与空间复杂度 如何衡量一个算法的好坏 long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) Fib(N-2); } 这是一个求斐波那契数列的函数,使用递归的方法求得,虽然代码看起来很简洁,但是简洁真的就好吗&#…...

Codeforces Round #848 (Div. 2)(A~D)
A. Flip Flop Sum给出一个只有1和-1的数组,修改一对相邻的数,将它们变为对应的相反数,修改完后数组的和最大是多少。思路:最优的情况是修改一对-1,其次是一个1一个-1,否则修改两个1。AC Code:#i…...
)
第十三届蓝桥杯Java B 组国赛 C 题——左移右移(AC)
目录1.左移右移1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围6.原题链接2.解题思路3.Ac_code1.左移右移 1.题目描述 小蓝有一个长度为 NNN 的数组, 初始时从左到右依次是 1,2,3,…N1,2,3, \ldots N1,2,3,…N 。 之后小蓝对这个数组进行了 MMM 次操作, 每次…...

第14篇:系列二—Java抽象类/接口/枚举
目录 1、继承的定义(Inheritance) 2、继承的优点 2.1 易维护性 2.2 复用性 2.3 条理性...
深入浅出C++ ——哈希
文章目录前言一、unordered系列关联式容器1. unordered_map2. unordered_set二、哈希1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决方法三、模拟实现unordered系列容器1. 哈希表的改造2. 模拟实现 unordered_set3. 模拟实现 unordered_map前言 在C11中,STL又提…...

Tina_Linux_系统裁剪_开发指南
文章目录Tina_Linux_系统裁剪_开发指南1 概述2 Tina系统裁剪简介2.1 boot0裁剪2.2 uboot裁剪2.3 内核裁剪2.3.1 删除不使用的功能2.3.2 删除不使用的驱动2.3.3 修改内核源代码2.3.3.1 size工具.2.3.3.2 ksize.py脚本2.3.3.3 nm命令2.3.3.4 kernel压缩方式.2.4 文件系统裁剪.2.4…...

算法刷题打卡第99天:至少在两个数组中出现的值
至少在两个数组中出现的值 难度:简单 给你三个整数数组 nums1、nums2 和 nums3 ,请你构造并返回一个 元素各不相同的 数组,且由 至少 在 两个 数组中出现的所有值组成。数组中的元素可以按 任意 顺序排列。 示例 1: 输入&…...

线程池面试题
1. 什么是线程池?为什么要使用线程池? 线程池是一种用于管理线程的技术,它可以在应用程序中重复使用一组线程来执行多个任务。线程池的优点包括提高应用程序的性能和可伸缩性、避免线程创建和销毁的开销、避免线程过多导致系统负担过重等。线…...

【学习笔记】NOIP爆零赛5
说实话是不想补题的。因为每一道题都贼难写,题解又通篇写着显然,然后自己天天搞竞赛又把注意力搞差了,调一道题又调半天,考试的题又难的要死 不会正解 ,部分分又写挂了 可能心态崩了就是从那场t1t1t1签到题考高精度数位…...

【数据结构】时间复杂度
🚀write in front🚀 📜所属专栏:初阶数据结构 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对…...

vector的基本使用
目录 介绍: vector iterator 的使用 增删查改 增(push_back insert): 删(pop_back erase): swap: vector的容量和扩容: 排序(sort): 介绍ÿ…...

剑指 Offer 55 - I. 二叉树的深度
摘要 剑指 Offer 55 - I. 二叉树的深度 一、深度优先搜索 如果我们知道了左子树和右子树的最大深度l和r,那么该二叉树的最大深度即为:max(l,r)1。 而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计…...
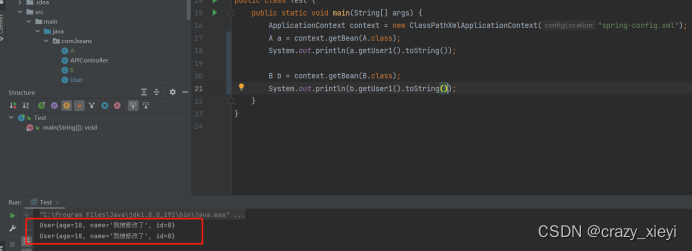
Bean的生命周期和作用域
Bean的生命周期Bean的执行流程:Bean 执行流程:启动Spring 容器 -> 实例化 Bean(分配内存空间,从无到有)-> Bean 注册到 Spring 中(存操作) -> 将 Bean 装配到需要的类中(取…...
TestNG和Junit的区别,测试框架该如何选择?
要想知道两个框架的区别,首先分别介绍一下两个框架。 TestNG是一个java中的开源自动化测试框架,其灵感来自JUnit和NUnit,TestNG还涵盖了JUnit4整个核心的功能,但引入了一些新的功能,使其功能更强大,使用更…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
