确知波束形成matlab仿真
阵列信号处理中的导向矢量
假设一均匀线性阵列,有N个阵元组成,满足:远场、窄带假设。

假设信源发射信号,来波方向为 θ \theta θ,第一个阵元接收到的信号为 x ( t ) x(t) x(t),则第 n n n个阵元接收的信号可以表示为 X = x ( t ) e j 2 π ∗ ( n − 1 ) d s i n θ λ X=x(t)e^{j2\pi*(n-1)\frac{dsin\theta}{\lambda}} X=x(t)ej2π∗(n−1)λdsinθ,可以得到阵列对信号的响应,即导向矢量(steering vector):
a ( θ ) = [ 1 , e j 2 π ∗ d s i n θ λ , e j 2 π ∗ 2 ∗ d s i n θ λ , . . . , e j 2 π ∗ ( N − 1 ) ∗ d s i n θ λ ] T a(\theta)=[1,e^{j2\pi*\frac{dsin\theta}{\lambda}},e^{j2\pi*2*\frac{dsin\theta}{\lambda}},...,e^{j2\pi*(N-1)*\frac{dsin\theta}{\lambda}}]^T a(θ)=[1,ej2π∗λdsinθ,ej2π∗2∗λdsinθ,...,ej2π∗(N−1)∗λdsinθ]T
那么阵列输出为: y = a ( θ ) x ( t ) y=a(\theta)x(t) y=a(θ)x(t)
matlab中可以一行代码来实现:
% Input :
% * N: 阵元数
% * theta:来波方向
% * dLembda:阵元间距与波长的比值,通常为1/2
% Output :
% * aTheta:导向矢量,列向量
aTheta = exp(1i*2*pi*dLembda*[0:N-1]'*sin(theta/180*pi));
确知波束形成
确知波束形成就是通过对各阵元接收到的信号进行加权求和的方式,使的波束指向一个确定的方向,经过波束形成之后,阵列接收的信号就由一个矩阵变为了一个向量,此时只是一个信号。假设来波方向为 θ \theta θ,确知波束形成的权重,就是导向矢量的埃尔米特转置,即共轭转置:
W = a ( θ ) H = [ 1 , e − j 2 π ∗ d s i n θ λ , e − j 2 π ∗ 2 ∗ d s i n θ λ , . . . , e − j 2 π ∗ ( N − 1 ) ∗ d s i n θ λ ] W=a(\theta)^{H}=[1,e^{-j2\pi*\frac{dsin\theta}{\lambda}},e^{-j2\pi*2*\frac{dsin\theta}{\lambda}},...,e^{-j2\pi*(N-1)*\frac{dsin\theta}{\lambda}}] W=a(θ)H=[1,e−j2π∗λdsinθ,e−j2π∗2∗λdsinθ,...,e−j2π∗(N−1)∗λdsinθ]
波束形成之后,输出信号为:
y = W X = W a ( θ ) x ( t ) y=WX=Wa(\theta)x(t) y=WX=Wa(θ)x(t)
静态波束形成其实就是空间滤波,它对指定方向上的信号进行加强和选择性通过,而对其他方向的来波信号进行抑制,例如有一个信源发出信号为 x 1 ( t ) x_1(t) x1(t)的波达方向为 θ 1 = 1 0 ∘ \theta_1=10^{\circ} θ1=10∘,而波束指向 θ 2 = 2 0 ∘ \theta_2=20^{\circ} θ2=20∘,此时
导向矢量(steering vector):
a ( θ 1 ) = [ 1 , e j 2 π ∗ d s i n θ 1 λ , e j 2 π ∗ 2 ∗ d s i n θ 1 λ , . . . , e j 2 π ∗ ( N − 1 ) ∗ d s i n θ 1 λ ] T a(\theta_1)=[1,e^{j2\pi*\frac{dsin\theta_1}{\lambda}},e^{j2\pi*2*\frac{dsin\theta_1}{\lambda}},...,e^{j2\pi*(N-1)*\frac{dsin\theta_1}{\lambda}}]^T a(θ1)=[1,ej2π∗λdsinθ1,ej2π∗2∗λdsinθ1,...,ej2π∗(N−1)∗λdsinθ1]T
那么阵列输出为: y = a ( θ 1 ) x 1 ( t ) y_=a(\theta_1)x_1(t) y=a(θ1)x1(t)。
指向 2 0 ∘ 20^{\circ} 20∘确知波束对阵元的加权的权重为:
W = a ( θ 2 ) H = [ 1 , e − j 2 π ∗ d s i n θ 2 λ , e − j 2 π ∗ 2 ∗ d s i n θ 2 λ , . . . , e − j 2 π ∗ ( N − 1 ) ∗ d s i n θ 2 λ ] W=a(\theta_2)^{H}=[1,e^{-j2\pi*\frac{dsin\theta_2}{\lambda}},e^{-j2\pi*2*\frac{dsin\theta_2}{\lambda}},...,e^{-j2\pi*(N-1)*\frac{dsin\theta_2}{\lambda}}] W=a(θ2)H=[1,e−j2π∗λdsinθ2,e−j2π∗2∗λdsinθ2,...,e−j2π∗(N−1)∗λdsinθ2]
波束形成之后,输出信号为:
y = W X = W a ( θ 1 ) x 1 ( t ) = ( a ( θ 2 ) ) T a ( θ 1 ) x 1 ( t ) = ( 1 ∗ 1 + e j ∗ 2 π d λ ( s i n θ 1 − s i n θ 2 ) + e j ∗ 2 π ∗ 2 ∗ d λ ( s i n θ 1 − s i n θ 2 ) + . . . + e j ∗ 2 π ∗ ( N − 1 ) ∗ d λ ( s i n θ 1 − s i n θ 2 ) ) x 1 ( t ) y=WX=Wa(\theta_1)x_1(t)=(a(\theta_2))^Ta(\theta_1)x_1(t)=(1*1+e^{j*2\pi \frac{d}{\lambda}(sin\theta_1-sin\theta_2)}+e^{j*2\pi *2* \frac{d}{\lambda}(sin\theta_1-sin\theta_2)}+...+e^{j*2\pi *(N-1)* \frac{d}{\lambda}(sin\theta_1-sin\theta_2)})x_1(t) y=WX=Wa(θ1)x1(t)=(a(θ2))Ta(θ1)x1(t)=(1∗1+ej∗2πλd(sinθ1−sinθ2)+ej∗2π∗2∗λd(sinθ1−sinθ2)+...+ej∗2π∗(N−1)∗λd(sinθ1−sinθ2))x1(t)
我们对其中的权重取绝对值进行分析,因为 θ 1 ≠ θ 2 \theta_1 \neq \theta_2 θ1=θ2 ,所以每一项进行加权后的绝对值都小于1,而只有第一项等于1:
∣ e j ∗ 2 π d λ ∗ n ∗ ( s i n θ 1 − s i n θ 2 ) ∣ < 1 , n = 2 , 3 , . . . , N − 1 |e^{j*2\pi \frac{d}{\lambda}*n*(sin\theta_1-sin\theta_2)}|<1,n=2,3,...,N-1 ∣ej∗2πλd∗n∗(sinθ1−sinθ2)∣<1,n=2,3,...,N−1
但是当波束指向方向与来波方向重合的时候,即 θ 1 = θ 2 = 2 0 ∘ \theta_1=\theta_2=20^{\circ} θ1=θ2=20∘的时候
y = W X = W a ( θ 1 ) x 1 ( t ) = ( a ( θ 2 ) ) T a ( θ 1 ) x 1 ( t ) = ( 1 + 1 + . . . + 1 ) x 1 ( t ) = N x 1 ( t ) y=WX=Wa(\theta_1)x_1(t)=(a(\theta_2))^Ta(\theta_1)x_1(t)=(1+1+...+1)x_1(t)=Nx_1(t) y=WX=Wa(θ1)x1(t)=(a(θ2))Ta(θ1)x1(t)=(1+1+...+1)x1(t)=Nx1(t)
其中 N N N为阵元个数,即信号 x 1 ( t ) x_1(t) x1(t)被增强 N N N倍。
阵列方向图
我们可以通过仿真,绘制方向图,来直观展示阵列的空间滤波响应,方向图定义为阵列输入为平面波的时候,阵列输出(通常只是考虑输出幅度或者功率与平面波入射角的关系)。一维线阵在阵列基线上的幅度方向图为:
G ( θ ) = ∣ W H a ( θ ) ∣ G(\theta)=|W^Ha(\theta)| G(θ)=∣WHa(θ)∣
功率方向图为:
G ( θ ) = ∣ W H a ( θ ) ∣ 2 G(\theta)=|W^Ha(\theta)|^2 G(θ)=∣WHa(θ)∣2
不管是幅度方向图还是功率方向图,都和阵列的权矢量有关,在工程中,分贝形式的方向图更为普遍,幅度方向图和功率方向图的分贝形式分别为:
G ( θ ) = 10 l g ∣ W H a ( θ ) ∣ G(\theta)=10lg|W^Ha(\theta)| G(θ)=10lg∣WHa(θ)∣
功率方向图为:
G ( θ ) = 20 l g ∣ ∣ W H a ( θ ) ∣ 2 G(\theta)=20lg||W^Ha(\theta)|^2 G(θ)=20lg∣∣WHa(θ)∣2
阵列方向图仿真
下面采用matlab仿真,绘制方向图,编写的方向图自定义函数
function Gtheta = DBF(elementNum,observaTheta,pointTheta,dLmbda,plotEnableHigh)
% 该函数用于产生方向图
% Author:huasir 2023.9.24 @Beijing
% Input :
% * elementNum: 阵元数
% * observaTheta:观测角度范围,例如[-90:0.1:90]
% * theta:来波方向
% * dLembda:阵元间距与波长的比值,通常为1/2
% Output :
% * GTheta:方向图
N = elementNum; %阵元数
theta = observaTheta; %观测角度范围
theta0 = pointTheta; %波形形成的方向
theta0 = theta0*pi/180;
theta = theta*pi/180;
d_lembda = dLmbda; %阵元间距比波长
a = exp(j*2*pi*d_lembda*(0:N-1)'*sin(theta)); %导向矢量
w = exp(j*2*pi*d_lembda*(0:N-1)'*sin(theta0)); %加权权向量
y = abs(w'*a);
%win = taylorwin(N); % 泰勒窗
%win = chebwin(N,30); %切比雪夫窗,抑制旁瓣
% ww = w.*win; %加窗操作
% y1 = abs(ww'*a); %加窗后的方向图
if plotEnableHigh == 1figure;%plot(theta*180/pi,20*log10(y/max(y)),'--',theta*180/pi,20*log10(y1/max(y1)),'-');plot(theta*180/pi,20*log10(y/max(y)),'linewidth',1);xlabel('方位角/°');ylabel('归一化功率方向图/dB');axis tight;% axistight 使得图形框图靠近数据grid on; %添加栅格线ylim([-40, 0]); % 为了限制y值范围,使得图像显示的更加合理title(sprintf('阵元数:%d,波束方向:%.0f°',N,pointTheta))
end
Gtheta = y; %返回方向图
end
在主函数中进行调用,主要参数如下:
| 参数 | Value |
|---|---|
| 阵元 | 8 |
| 波束方向 | 10° |
| 阵元间距 | 1 / 2 λ 1/2\lambda 1/2λ |
主函数中进行调用:
close all; clear all; clc;
Gtheta = DBF(8,(-90:0.1:90),10,1/2,1);
绘制的方向图如下:

相关文章:

确知波束形成matlab仿真
阵列信号处理中的导向矢量 假设一均匀线性阵列,有N个阵元组成,满足:远场、窄带假设。 图1. 均匀线性阵模型 假设信源发射信号,来波方向为 θ \theta θ,第一个阵元接收到的信号为 x ( t ) x(t) x(t),则第…...

并发编程相关面试题
线程基础 线程和进程的区别: ----------------------------------------------------------------------- 创建线程的方式: 1 继承Thread类 2 实现runnable接口 3 实现callable 接口(有返回值的) 4 线程池创建线程 ------…...
Cpp/Qt-day050921Qt
目录 实现使用数据库的登录注册功能 头文件: registrwidget.h: widget.h: 源文件: registrwidget.c: widget.h: 效果图: 思维导图 实现使用数据库的登录注册功能 头文件: registrwidget.h: #ifndef REGISTRWIDGET_H #de…...

视频汇聚/视频云存储/视频监控管理平台EasyCVR分发rtsp流起播慢优化步骤详解
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...

ElementUI之登陆+注册->饿了吗完成用户登录界面搭建,axios之get请求,axios之post请求,跨域,注册界面
饿了吗完成用户注册登录界面搭建axios之get请求axios之post请求跨域 1.饿了吗完成用户注册登录界面搭建 将端口号8080改为8081 导入依赖,在项目根目录使用命令npm install element-ui -S,添加Element-UI模块 -g:将依赖下载node_glodal全局依…...
2023华为杯研究生数学建模研赛E题出血脑卒中完整论文(含28个详细预处理数据及结果表格)
大家好呀,从发布赛题一直到现在,总算完成了全国研究生数学建模竞赛(数模研赛)E题完整的成品论文。 本论文可以保证原创,保证高质量。绝不是随便引用一大堆模型和代码复制粘贴进来完全没有应用糊弄人的垃圾半成品论文。…...

Java中的继承是什么?
在Java中,继承是一种面向对象编程的概念,它允许一个类(称为子类或派生类)继承另一个类(称为父类或基类)的属性和方法。通过继承,子类可以获得父类的属性和方法,并且可以添加自己的特…...

Python - flask后端开发笔记
Flask入门 有一篇很全面的博客可以参考:Python Flask Web 框架入门 跨域问题处理 from flask_cors import CORS CORS(app,supports_credentialsTrue,origins[url], # 前端url列表 ) 文件发送 from flask import send_from_directory app.route(/download) …...

Flutter实现PS钢笔工具,实现高精度抠图的效果。
演示: 代码: import dart:ui;import package:flutter/material.dart hide Image; import package:flutter/services.dart; import package:flutter_screenutil/flutter_screenutil.dart; import package:kq_flutter_widgets/widgets/animate/stack.dart…...
苏宁滑块验证
网址:https://passport.suning.com/ids/login总结一下,别被他的表面现象给骗了,这玩意儿,个人认为,腾讯的都没法跟他比!!! 难点:动态混淆,vmp,图片…...

c语言。。。
gcc thread.c -lpthread -o app -fexec-charsetgbkthread.c为当前目录下编写的c代码 代码中引入了<pthread.h>线程库,所以要加上-lpthread -o app 输出.exe的c可执行文件,文件名为app -fexec-charsetgbk 设置编码方式,防止控制台输出中…...

vue-cli创建项目、vue项目目录结(运行vue项目)、ES6导入导出语法、vue项目编写规范
vue-cli创建项目、vue项目目录结构、 ES6导入导出语法、vue项目编写规范 1 vue-cli创建项目 1.1 vue-cli 命令行创建项目 1.2 使用vue-cli-ui创建 2 vue项目目录结构 2.1 运行vue项目 2.2 vue项目的目录结构 3 es6导入导出语法 4 vue项目编写规范 4.1 修改项目 4.2 以后…...

QT读取DLL加载算法
有这样一个场景,我有一个GUI软件,把他想象成PS软件,集成了很多工具。现在我要添加新算法(PS工具),该怎么办? 有三种办法: 第一种我把新算法代码加到项目中,编译整个项目。 第二种,新…...

HTTPX-用于Python的下一代HTTP客户端
1、前言 在使用 Python 进行接口自动化时,大多数都会使用 requests 模块,requests 是一个常用的 HTTP 请求库,可以方便地向网站发送 HTTP 请求,并获取响应结果。 本篇将介绍 Python 的下一代 HTTP 客户端 - HTTPX 2、简介 HTT…...

[LLM+AIGC] 01.应用篇之中文ChatGPT初探及利用ChatGPT润色论文对比浅析(文心一言 | 讯飞星火)
近年来,人工智能技术火热发展,尤其是OpenAI在2022年11月30日发布ChatGPT聊天机器人程序,其使用了Transformer神经网络架构(GPT-3.5),能够基于在预训练阶段所见的模式、统计规律和知识来生成回答,…...
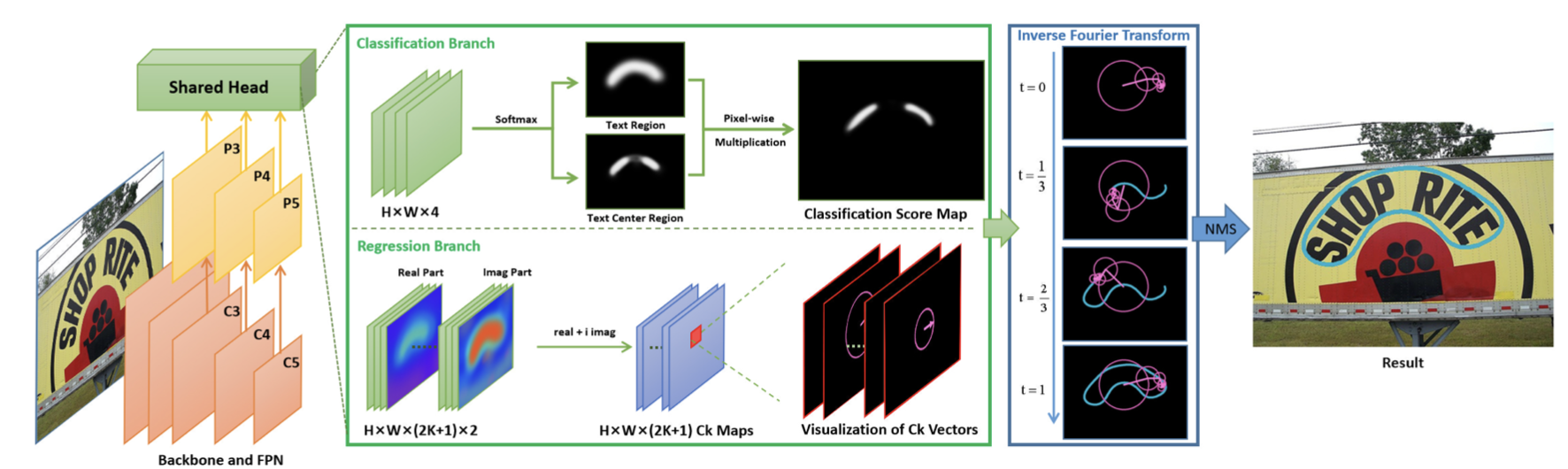
OCR -- 文本检测
目标检测: 不仅要解决定位问题,还要解决目标分类问题,给定图像或者视频,找出目标的位置(box),并给出目标的类别; 文本检测: 给定输入图像或者视频,找出文本的…...
【系统架构】软件可靠性基础知识
导读:本文整理关于软件可靠性基础知识构建系统架构知识体系。完整和扎实的系统架构知识体系是作为架构设计的理论支撑,基于大量项目实践经验基础上,不断加深理论体系的理解,从而能够创造新解决系统相关问题。 目录 1、软件可靠性…...

相机Camera
Camera需与SurfaceView配合使用 Camera类常用方法: Camera.open() 创建Camera实例,打开相机 getParameters() 获取相机参数 release() 释放相机资源 setParameters(Camera.Parameters parameters) 设置相机参数 setPreviewDisplay(SurfaceHolder holde…...
洛谷P8815:逻辑表达式 ← CSP-J 2022 复赛第3题
【题目来源】https://www.luogu.com.cn/problem/P8815https://www.acwing.com/problem/content/4733/【题目描述】 逻辑表达式是计算机科学中的重要概念和工具,包含逻辑值、逻辑运算、逻辑运算优先级等内容。 在一个逻辑表达式中,元素的值只有两种可能&a…...

ElementUI实现登录注册+axios全局配置+CORS跨域
一、搭建项目 1.1 安装 Element-UI 先确保是否安装了vue-cli脚手架工具 !!! 安装vue脚手架可以看看我的上一篇博客 构建好项目后通过npm安装element-ui cd 项目根路径 #进入新建项目的根目录 npm install element-ui -S #安装…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
