博弈论——反应函数
反应函数
1 引言
谢老师的《经济博弈论》书中对反应函数并没有给出一般笼统的定义,而是将其应用与古诺模型并给出了相关解释:反应函数是指在无限策略的古诺博弈模型中,博弈方的策略有无限多种,因此各个博弈方的最佳对策也有无限种,它们之间往往构成一种连续函数的关系,把这个连续函数称为反应函数。
有趣的是百度百科对于反应函数的定义与谢老师书上的一致,但是在该词条正文中,还有一句话是:在经济学中,反应函数在博弈论古诺模型中有相应的应用,在假设竞争对手产生了给定产出水平的情况下,反应函数可以得出你的最佳产出水平。
这句话其实比较通俗易懂得解释了反应函数的定义,就是说:反应函数就是当一个企业做经营决策(如产量决策、价格决策等)时,对于给定的其他竞争企业的经营决策,所做出的反应,表明这一反应关系的函数。大白话就是,你做了决策后,我根据你的决策做出我的决策,那描述“根据你的决定,做出我的决定”的关系的函数,称为反应函数。
2 反应函数
根据你的先手,决定对我最有利的后手,是反应函数最关键的地方。我们以前一篇文章的连续产量古诺模型为例:
在上述两寡头古诺模型中,对厂商2的任意产量q2 ,厂商1的最佳对策产量q1,是下面最大化问题的解:
m a x q 1 π 1 = m a x q 1 ( − q 1 2 − c q 1 − q 1 q 2 + 8 q 1 ) \underset{q_1}{max}π_1=\underset{q_1}{max}(-q_1^2-cq_1-q_1 q_2+8q_1) q1maxπ1=q1max(−q12−cq1−q1q2+8q1)
也就是给定 q 2 q_2 q2,求能让厂商1得到最优利润的 q 1 q_1 q1。
令 π 1 π_1 π1对 q 1 q_1 q1求一阶导,并等于0,得到:
− 2 q 1 − c − q 2 + 8 = 0 -2q_1-c-q_2+8=0 −2q1−c−q2+8=0
即:
q 1 = 8 − c − q 2 2 q_1=\frac{8-c-q_2}{2} q1=28−c−q2
令:
q 1 = 8 − c − q 2 2 = R 1 ( q 2 ) q_1=\frac{8-c-q_2}{2}=R_1 (q_2) q1=28−c−q2=R1(q2)
得到的这个函数 R ( q 2 ) R(q_2) R(q2)是对于厂商2的每一个可能产量,厂商1最佳产量的计算公式。这个函数称为厂商1对厂商⒉产量的“反应函数”(reaction function)。
同理,可求出厂商2对厂商1产量 q 1 q1 q1的反应函数为:
q 2 = 8 − c − q 1 2 = R 2 ( q 1 ) q_2=\frac{8-c-q_1}{2}=R_2 (q_1) q2=28−c−q1=R2(q1)
显而易见, R 1 ( q 2 ) R_1 (q_2) R1(q2)、 R 2 ( q 1 ) R_2 (q_1) R2(q1)这两个反应函数都是线性函数(linear function),我们在坐标平面上用两条直线表示出来,更好得进行研究。
3 图像
首先我们分别确定两个线性函数在坐标系上的两点,以数对 ( q 1 , q 2 ) (q_1,q_2) (q1,q2)表示。对于 q 1 = R 1 ( q 2 ) q_1=R_1 (q_2) q1=R1(q2),其经过 ( 8 − c 2 , 0 ) (\frac{8-c}{2},0) (28−c,0)、 ( 0 , 8 − c ) (0,8-c) (0,8−c)两点;对于 q 2 = R 2 ( q 1 ) q_2=R_2 (q_1) q2=R2(q1),其经过 ( 8 − c , 0 ) (8-c,0) (8−c,0)、 ( 0 , 8 − c 2 ) (0,\frac{8-c}{2}) (0,28−c)两点,如下图所示:
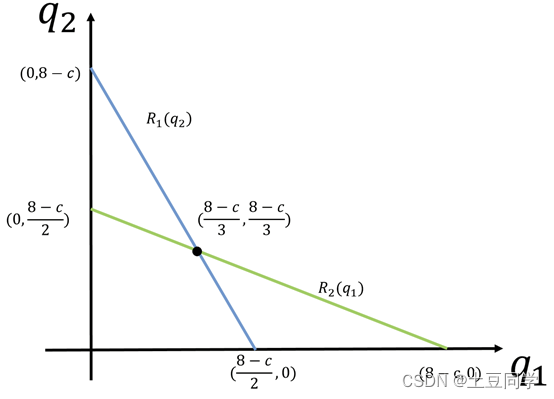
根据图像可以看出:
- 当一方产量选择为0时,另一方的最佳反应为 8 − c 2 \frac{8-c}{2} 28−c,这正是上篇文章中提到的实现市场总利益最大的产量,这时候等于一个厂商垄断市场;
- 当一方产量达到 8 − c 8-c 8−c时,另一方被迫生产0,因为后者坚持生产无利可图.
在两个反应函数对应的两条直线上,只有交点 ( 8 − c 3 , 8 − c 3 ) (\frac{8-c}{3},\frac{8-c}{3}) (38−c,38−c)代表的产量组合,才是由相互对对方的最佳反应构成的。
需要注意的是, q 1 = R 1 ( q 2 ) q_1=R_1 (q_2) q1=R1(q2)上其他所有点 ( q 1 , q 2 ) (q_1,q_2) (q1,q2)代表了只有 q 1 q_1 q1是对 q 2 q_2 q2的最佳反应, q 2 q_2 q2不是对 q 1 q_1 q1的最佳反应;而 q 2 = R 2 ( q 1 ) q_2=R_2 (q_1) q2=R2(q1)上其他点代表了只有 q 2 q_2 q2是对 q 1 q_1 q1的最佳反应, q 1 q_1 q1不是对 q 2 q_2 q2的最佳反应。因此,根据纳什均衡的定义,当 ( q 1 , q 2 ) = ( 8 − c 3 , 8 − c 3 ) (q_1,q_2)=(\frac{8-c}{3},\frac{8-c}{3}) (q1,q2)=(38−c,38−c),即 q 1 q_1 q1、 q 2 q_2 q2相互是对于对方的最佳反应,是该博弈唯一的纳什均衡。这与上篇文章通过数理推导得到的结论一致。
4 结语
得益是策略多元连续函数的博弈,都可以求每个博弈方的反应函数,解出各博弈方反应函数的交点就是纳什均衡。这种用反应函数求纳什均衡的方法,称为“反应函数法”。
相关文章:

博弈论——反应函数
反应函数 1 引言 谢老师的《经济博弈论》书中对反应函数并没有给出一般笼统的定义,而是将其应用与古诺模型并给出了相关解释:反应函数是指在无限策略的古诺博弈模型中,博弈方的策略有无限多种,因此各个博弈方的最佳对策也有无限…...
UE5读取json文件
一、下载插件 在工程中启用 二、定义读取外部json文件的函数,参考我之前的文章 ue5读取外部文件_艺菲的博客-CSDN博客 三、读取文件并解析为json对象 这里Load Text就是自己定义的函数,ResourceBundle为一个字符串常量,通常是读取的文件夹…...
Vue中的插槽--组件复用,内容自定义
插槽 文章目录 插槽插槽-默认插槽插槽-后备内容(设置默认值)插槽-具名插槽插槽–作用域插槽 插槽-默认插槽 作用:让组件内部的一些结构支持自定义 需求:要在页面中显示一个对话框,封装成一个组件(对话框有很多功能是类…...

完全指南:mv命令用法、示例和注意事项 | Linux文件移动与重命名
文章目录 mv命令使用指南1. 简介什么是mv命令?mv命令的作用和功能是什么? 2. 基本用法基本语法格式如何移动文件?如何重命名文件?如何移动和重命名目录? 3. 高级用法使用通配符进行批量移动和重命名使用选项进行文件移…...
gitee生成公钥和远程仓库与本地仓库使用验证
参考文档: https://help.gitee.com/base/account/SSH%E5%85%AC%E9%92%A5%E8%AE%BE%E7%BD%AE(1)通过命令ssh-keygen 生成SSH key -t key类型 -c注释 ssh-keygen -t ed25519 -C "Gitee SSH Key" (2)按三次回车 (3)查看生成的 SSH 公钥和私钥: …...

请求后端接口413
当在进行HTTP请求时出现"413 Request Entity Too Large"错误时,通常是因为请求体的大小超过了服务器的配置限制。这个错误提示表明服务器拒绝接受过大的请求。 此时一般还未到后端服务,是被后端的ngnix代理服务器拦截的,所以可以检…...
HarmonyOS之 开发环境搭建
一 鸿蒙简介: 1.1 HarmonyOS是华为自研的一款分布式操作系统,兼容Android,但又区别Android,不仅仅定位于手机系统。更侧重于万物物联和智能终端,目前已更新到4.0版本。 1.2 HarmonyOS软件编程语言是ArkTS,…...
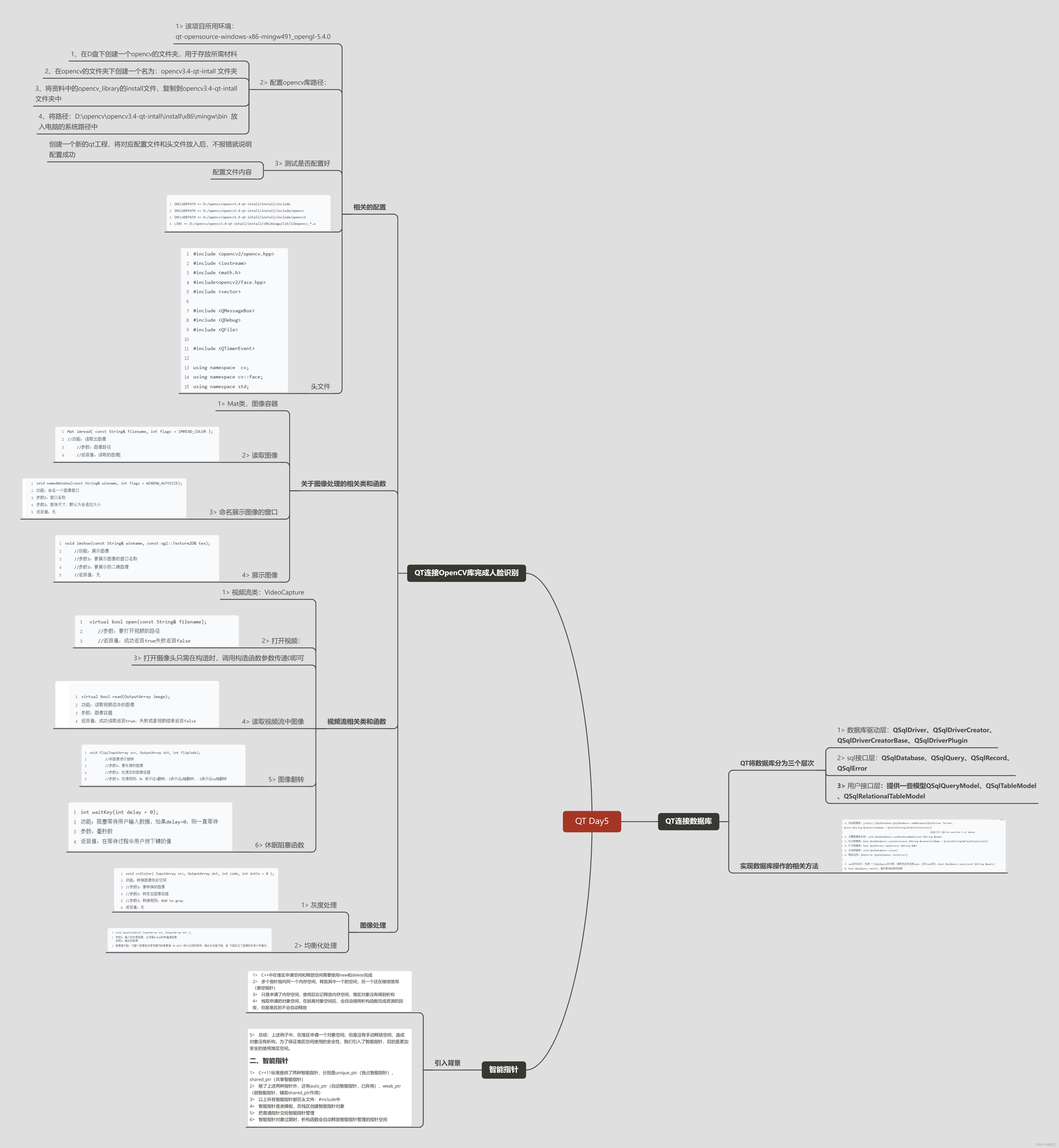
QTC++ day12
注册登录界面 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QIcon> #include <QPushButton> #include <QLineEdit> #include <QLabel> #include <QDebug> #include <QMessageBox>//消息对话框类 #inc…...

Vue3中使用Proxy API取代defineProperty API的原因
目录 一、前言 二、defineProperty API的限制和问题 三、Proxy API的优势和特性 四、Vue3.0中使用Proxy API的原因 五、Proxy API的局限性和注意事项 一、前言 Vue3.0是Vue.js框架的最新版本,它在底层进行了许多重要的改进。其中最引人注目的变化之一是它转而…...
构建工具Webpack简介
一、构建工具 当我们习惯了Node中使用ES模块化编写代码以后,用原生的HTML、CSS、JS这些东西会感觉到各种不便。比如:不能放心的使用模块化规范(浏览器兼容性问题)、即使可以使用模块化规范也会面临模块过多时的加载问题。 这时候…...
Docker部署单点Elasticsearch与Kibana
一 、 创建网络 因为需要部署kibana容器,因此需要让es和kibana容器互联。这里创建一个网络: docker network create es-net # 创建一个网络名称为:es-net 二 、拉取并加载镜像 方式一 docker pull elasticsearch:7.12.1 版本为elasticsearch的7…...
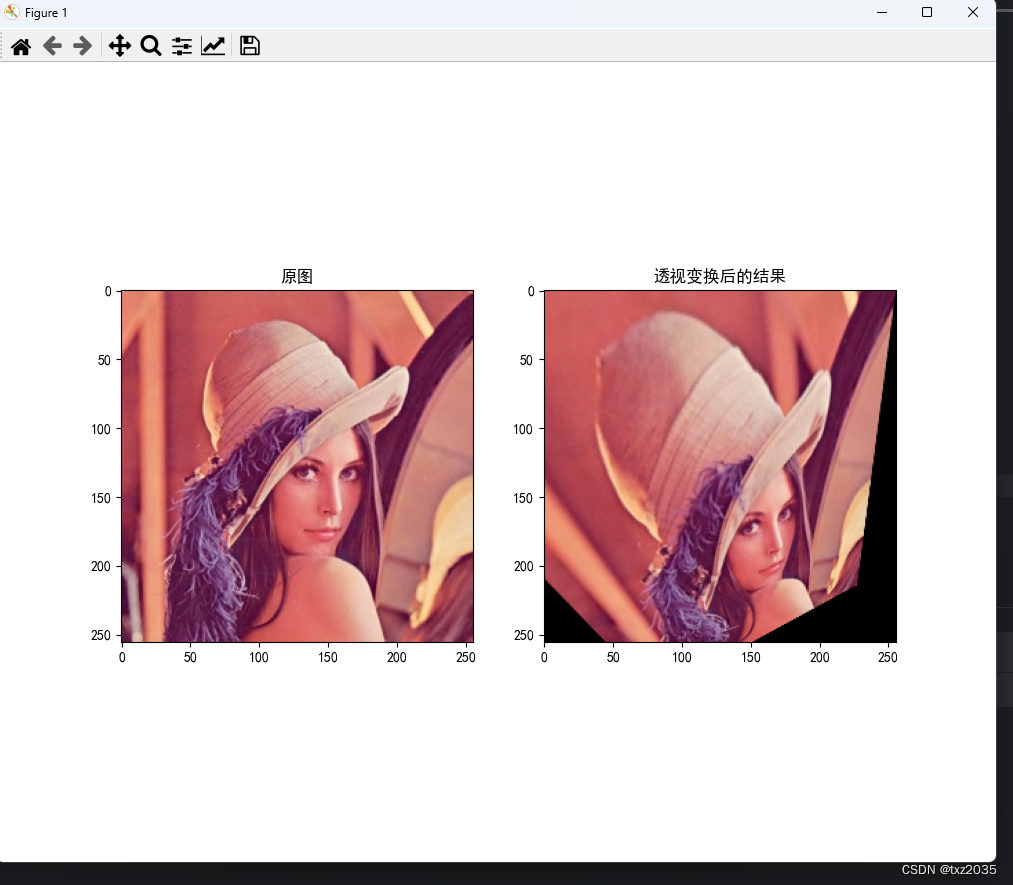
opencv实现仿射变换和透射变换
##1, 什么是仿射变换? 代码实现 import numpy as np import cv2 as cv import matplotlib.pyplot as plt#设置字体 from pylab import mpl mpl.rcParams[font.sans-serif] [SimHei]#图像的读取 img cv.imread("lena.png")#仿射变换 row…...
抖音seo账号矩阵源码系统
1. 开通多个抖音账号,并将它们归纳为一个账号矩阵系统。 2. 建立一个统一的账号管理平台,以便对这些账号进行集中管理,包括账号信息、内容发布、社区交互等。 3. 招募专业的运营团队,对每个账号进行精细化运营,包括内…...

性能优化之防抖
方法1:利用lodash库提供的防抖来处理 方法2:手写一个防抖函数来处理 需求:鼠标在盒子上移动,鼠标停止500ms之后,里面的数字才会变化1 方法一:利用lodash库实现防抖 <!DOCTYPE html> <html lang&…...

postgresql用户和角色
postgresql用户和角色 简述创建角色角色属性登录特权超级用户创建数据库创建角色启动复制密码修改角色属性 对象授权撤销授权组和成员删除角色 简述 PostgreSQL 通过角色的概念来控制数据库的访问权限。角色又包含了两种概念,具有登录 权限的角色称为用户ÿ…...
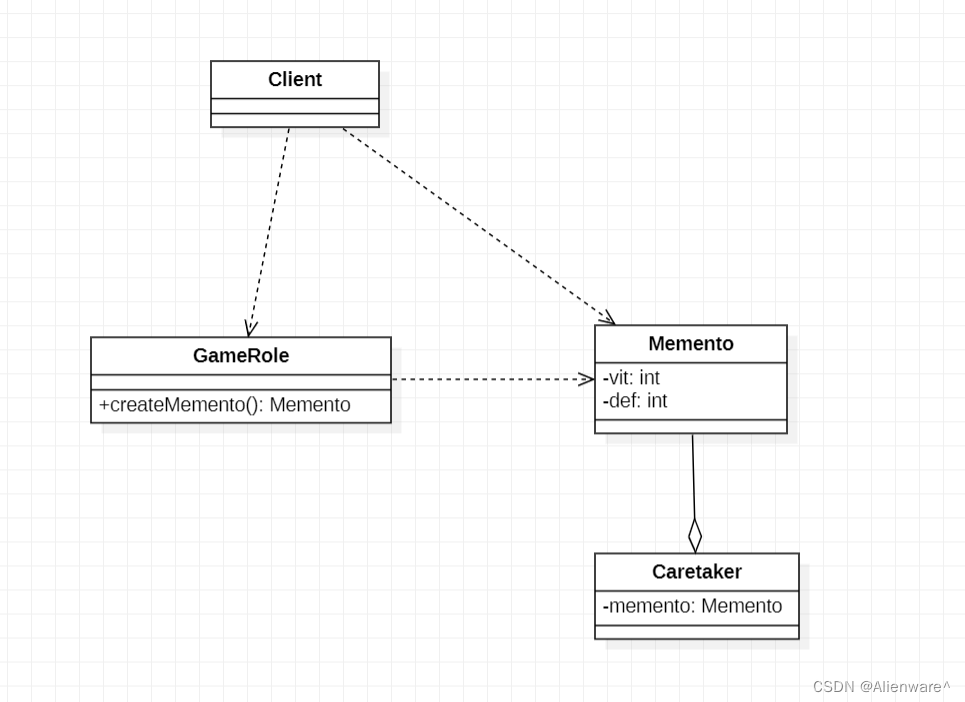
设计模式之备忘录模式
文章目录 游戏角色状态恢复问题传统方案解决游戏角色恢复传统的方式的问题分析备忘录模式基本介绍游戏角色恢复状态实例备忘录模式的注意事项和细节 游戏角色状态恢复问题 游戏角色有攻击力和防御力,在大战 Boss 前保存自身的状态(攻击力和防御力),当大…...
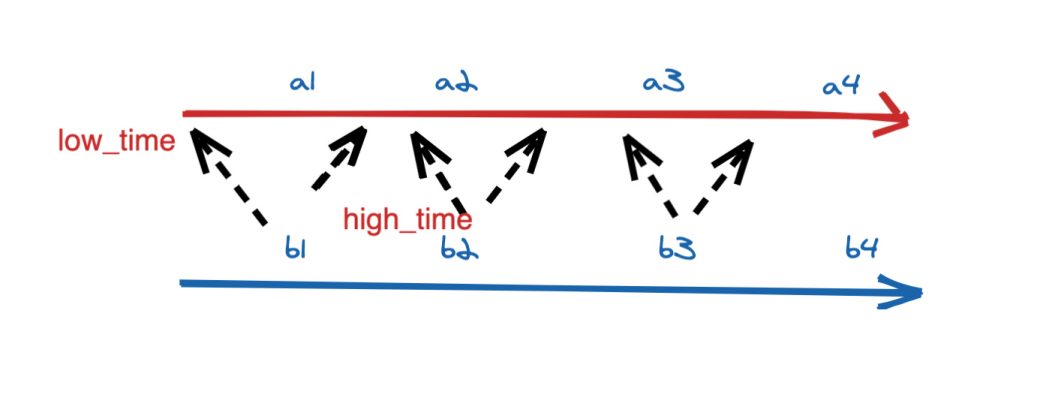
大数据Flink(八十八):Interval Join(时间区间 Join)
文章目录 Interval Join(时间区间 Join) Interval Join(时间区间 Join) Interval Join 定义(支持 Batch\Streaming):Interval Join 在离线的概念中是没有的。Interval Join 可以让一条流去 Jo…...
)
数字IC笔试千题解--判断题篇(五)
前言 出笔试题汇总,是为了总结秋招可能遇到的问题,做题不是目的,在做题的过程中发现自己的漏洞,巩固基础才是目的。 所有题目结果和解释由笔者给出,答案主观性较强,若有错误欢迎评论区指出,资料…...

Kubernetes(k8s)上搭建一主两从的mysql8集群
Kubernetes上搭建一主两从的mysql8集群 环境准备搭建nfs服务器安装NFS暴露nfs目录开启nfs服务器 安装MySQL集群创建命名空间创建MySQL密码的Secret安装MySQL主节点创建pv和pvc主节点的配置文件部署mysql主节点 安装第一个MySQL Slave节点创建pv和pvc第一个从节点配置文件部署my…...
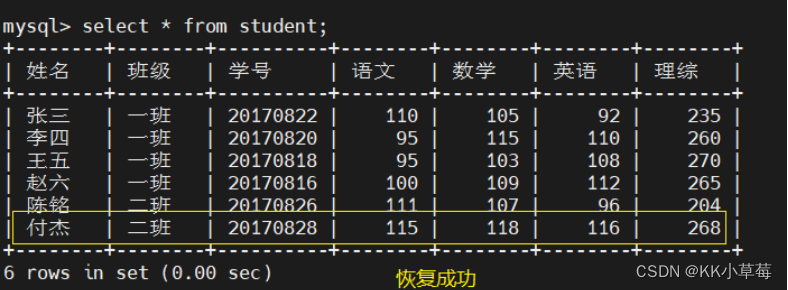
MySQL备份与恢复
MySQL备份与恢复一、备份1、数据备份的重要性2、数据备份分类2.1 物理备份2.2 逻辑备份 3、数据库备份策略4、常用的备份方法和工具5、数据库上云迁移 二、数据库完全备份1、简介2、物理冷备份与恢复2.1 物理冷备份2.2 备份恢复2.3 补充知识date 3、mysqldump备份与恢复3.1 完全…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
