线性代数基础-行列式
一、行列式之前的概念
1.全排列:
把n个不同的元素排成一列,称为n个元素的全排列,简称排列
(实际上就是我们所说的排列组合,符号是A,arrange)
2.标准序列:
前一项均小于后一项的序列就是标准序列
比如 1,3,6,7,9就是标准序列
3.逆序数:
序列中满足前一项大于后一项的数对个数
比如有一个序列:{1,6,9,2,3,4}
遍历该序列,看每个数之前有几个数比它大,加和就是逆序数的值
4.奇偶排列
排列的奇偶性与逆序数的奇偶性相同
5.对换
将序列里任意两个元素交换,这个过程叫对换
对换相邻元素的,称为“相邻对换”
经过任一次对换,排列的奇偶性改变
奇排列变成标准序列的对换次数是奇数,偶排列变成标准序列的对换次数是偶数
二、N阶行列式的展开
∣ a b c d ∣ = a d − b c \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad-bc acbd =ad−bc
有n行n列的这样的式子是n阶行列式,上图为二阶行列式
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = ( a 11 ∗ a 22 ∗ a 33 ) − ( a 11 ∗ a 23 ∗ a 32 ) + ( a 12 ∗ a 23 ∗ a 31 ) − ( a 12 ∗ a 21 ∗ a 32 ) + ( a 13 ∗ a 21 ∗ a 32 ) − ( a 13 ∗ a 22 ∗ a 31 ) \begin{vmatrix} a11 & a12&a13 \\ a21 & a22&a23\\ a31&a32&a33 \end{vmatrix} = (a11*a22*a33)-(a11*a23*a32)+(a12*a23*a31)-(a12*a21*a32)+(a13*a21*a32)-(a13*a22*a31) a11a21a31a12a22a32a13a23a33 =(a11∗a22∗a33)−(a11∗a23∗a32)+(a12∗a23∗a31)−(a12∗a21∗a32)+(a13∗a21∗a32)−(a13∗a22∗a31)
而行列式的值应按照以下规则计算
按**序列奇偶性(见上文)**决定符号,并逐行把数字相乘:

我们可以把矩阵理解为一个值,甚至常数,所以它满足我们学过的一切乘法,加法性质
三、三角行列式
主对角线:左上到右下
上三角行列式的主对角线下方都是0,行列式值等于主对角线乘积
注意:左下到右上不是主对角线
1.三角行列式
上三角行列式
∣ 1 2 3 0 1 2 0 0 2 ∣ = 1 ∗ 1 ∗ 2 \begin{vmatrix} 1 & 2 &3\\ 0 & 1&2\\ 0&0&2 \end{vmatrix} = 1 * 1 *2 100210322 =1∗1∗2
下三角行列式
∣ 1 0 0 4 1 0 3 1 2 ∣ = 1 ∗ 1 ∗ 2 \begin{vmatrix} 1 & 0 &0\\ 4 & 1&0\\ 3&1&2 \end{vmatrix} = 1 * 1 *2 143011002 =1∗1∗2
对角行列式
∣ 1 0 0 0 1 0 0 0 2 ∣ = 1 ∗ 1 ∗ 2 \begin{vmatrix} 1 & 0 &0\\ 0 & 1&0\\ 0&0&2 \end{vmatrix} = 1 * 1 *2 100010002 =1∗1∗2
四、行列式的性质
1.转置
对每一列,从上到下书写到行上,行列式的值不变
D = ∣ a b c d e f g h i ∣ = D T = ∣ a d g b e h c f i ∣ D = \begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} =D^T= \begin{vmatrix} a & d &g\\ b & e&h\\ c&f&i \end{vmatrix} D= adgbehcfi =DT= abcdefghi
2.交换
我们可以交换行列式的任意两行或者两列,但是会导致值变为相反数
推论1:若行列式D交换一次后,仍等于D,则D=0
推论2:若行列式有两行(列)相等,则行列式为0(交换后D=-D)
∣ a b c d e f g h i ∣ = ( − 1 ) ∗ ∣ a b c g h i d e f ∣ \begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} = (-1)* \begin{vmatrix} a & b &c\\ g & h&i\\ d & e&f \end{vmatrix} adgbehcfi =(−1)∗ agdbhecif
3.提取
我们可以把任意一个行或者一列的系数提取到行列式之前
推论:若两行(列)成比例,则行列式为0
∣ 2 a 2 b 2 c 2 d 2 e 2 f g h i ∣ = 2 ∗ ∣ 2 a 2 b 2 c d e f g h i ∣ \begin{vmatrix} 2a &2 b &2c\\ 2d & 2e&2f\\ g&h&i \end{vmatrix} =2* \begin{vmatrix} 2a & 2b &2c\\ d & e&f\\ g&h&i \end{vmatrix} 2a2dg2b2eh2c2fi =2∗ 2adg2beh2cfi
4.拆分
∣ a + x b + y c + z d + w ∣ = ∣ a b + y c d + w ∣ + ∣ x b + y z d + w ∣ \begin{vmatrix} a +x& b+y\\ c +z& d+w\\ \end{vmatrix} = \begin{vmatrix} a & b+y\\ c & d+w\\ \end{vmatrix} + \begin{vmatrix} x& b+y\\ z& d+w\\ \end{vmatrix} a+xc+zb+yd+w = acb+yd+w + xzb+yd+w
我们可以把行列式任意行(列)拆分成和的形式,然后转换为行列式的和
但是要注意我们每次只能拆分一行(列),多行(列)拆分是错误的
∣ a + x b + y c + z d + w ∣ = ∣ a b c d ∣ + ∣ x y z w ∣ \cancel{ \begin{vmatrix} a +x& b+y\\ c +z& d+w\\ \end{vmatrix} = \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} + \begin{vmatrix} x& y\\ z& w\\ \end{vmatrix}} a+xc+zb+yd+w = acbd + xzyw
5.调整
把任意一行(列)乘以k之后可以加到另一行(列)上,行列式不变
通常这样得到三角行列式来快捷计算
∣ a b c d e f g h i ∣ = ∣ a b c d + k ∗ a e + k ∗ b f + k ∗ c g h i ∣ ( k 任取 ) \begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} = \begin{vmatrix} a & b &c\\ d+k *a & e+k*b&f+k*c\\ g&h&i \end{vmatrix} (k任取) adgbehcfi = ad+k∗agbe+k∗bhcf+k∗ci (k任取)
例如我们可以轻易把某些行列式调整为三角行列式
∣ 1 1 2 4 3 1 3 2 2 ∣ = ∣ 1 1 2 0 − 1 − 7 0 − 1 − 4 ∣ = ∣ 1 1 2 0 − 1 − 7 0 0 3 ∣ = 1 ∗ ( − 1 ) ∗ 3 = − 3 \begin{vmatrix} 1 & 1 &2\\ 4 & 3&1\\ 3&2&2 \end{vmatrix} = \begin{vmatrix} 1 & 1 &2\\ 0 & -1&-7\\ 0&-1&-4 \end{vmatrix} = \begin{vmatrix} 1 & 1 &2\\ 0 & -1&-7\\ 0&0&3 \end{vmatrix} = 1*(-1)*3 = -3 143132212 = 1001−1−12−7−4 = 1001−102−73 =1∗(−1)∗3=−3
五、行列式的余子式和代数余子式
1.余子式
D = ∣ a b c d e f g h i ∣ D =\begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} D= adgbehcfi
M i j 是把 D 划去第 i 行 j 列的 ( n − 1 ) 阶行列式 M_{ij}是把D划去第i行j列的(n-1)阶行列式 Mij是把D划去第i行j列的(n−1)阶行列式
M 22 = ∣ a b c d e f g h i ∣ = ∣ a c g i ∣ M_{22} = \begin{vmatrix} a & \cancel{b} &c\\ \cancel{d} & \cancel{e} & \cancel{f} \\ g& \cancel{h} &i \end{vmatrix} = \begin{vmatrix} a &c\\ g & i\\ \end{vmatrix} M22= ad gb e h cf i = agci
2.代数余子式
A i j = ( − 1 ) i + j M i j A_{ij} = (-1)^{i+j} M_{ij} Aij=(−1)i+jMij
3.按行或按列展开
D n = a i 1 A i 1 + a i 2 A i 2 + . . . + a i n A i n D_{n}=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in} Dn=ai1Ai1+ai2Ai2+...+ainAin
这是按行展开,其实就是对某一行遍历,然后划掉当前元素所在行列求代数余子式,然后乘当前位置的值,按列展开同理。
六、特殊行列式
1.和固定型
D n = ∣ a b b . . . b b a b . . . b b b a . . . b . . . . . . . . . . . . . . . . . . . . . . . . . . . b b b . . . b a ∣ = ∣ a + n b a + n b a + n b . . . a + n b b a b . . . b b b a . . . b . . . . . . . . . . . . . . . . . . . . . . . . . . . b b b . . . b a ∣ D_{n} =\begin{vmatrix} a & b &b&...&b\\ b & a&b&...&b\\ b&b&a&...&b\\ ...&...&...&...&...\\ ...&...&...&...&b\\ b&b&...&b&a\\ \end{vmatrix} = \begin{vmatrix} a+nb & a+nb &a+nb&...&a+nb\\ b & a&b&...&b\\ b&b&a&...&b\\ ...&...&...&...&...\\ ...&...&...&...&b\\ b&b&...&b&a\\ \end{vmatrix} Dn= abb......bbab......bbba........................bbbb...ba = a+nbbb......ba+nbab......ba+nbba........................ba+nbbb...ba
= ( a + n b ) ∣ 1 1 1 . . . 1 b a b . . . b b b a . . . b . . . . . . . . . . . . . . . . . . . . . . . . . . . b b b . . . b a ∣ =(a+nb) \begin{vmatrix} 1 & 1 &1&...&1\\ b & a&b&...&b\\ b&b&a&...&b\\ ...&...&...&...&...\\ ...&...&...&...&b\\ b&b&...&b&a\\ \end{vmatrix} =(a+nb) 1bb......b1ab......b1ba........................b1bb...ba
接下来就可以愉快的用第一行把行列式消成三角了
= ( a + n b ) ∣ 1 1 1 . . . 1 0 a − b 0 . . . 0 0 0 a − b . . . 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . 0 0 0 . . . 0 a − b ∣ = ( a − b ) n − 1 =(a+nb) \begin{vmatrix} 1 & 1 &1&...&1\\ 0 & a-b&0&...&0\\ 0&0&a-b&...&0\\ ...&...&...&...&...\\ ...&...&...&...&0\\ 0&0&...&0&a-b\\ \end{vmatrix} = (a-b)^{n-1} =(a+nb) 100......01a−b0......010a−b........................0100...0a−b =(a−b)n−1
2.范德蒙德行列式
D n = ∣ x 1 0 x 2 0 x 3 0 . . . x n 0 x 1 1 x 2 1 x 3 1 . . . x n 1 x 1 2 x 2 2 x 3 2 . . . x n 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . x n n − 1 x 1 n x 2 n x 3 n . . . x n n ∣ = ∣ 1 1 1 . . . 1 x 1 1 x 2 1 x 3 1 . . . x n 1 x 1 2 x 2 2 x 3 2 . . . x n 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . x n n − 1 x 1 n x 2 n x 3 n . . . x n n ∣ D_{n} = \begin{vmatrix} x_1^0 & x_2^0 &x_3^0&...&x_n^0\\ x_1^1 & x_2^1 &x_3^1&...&x_n^1\\ x_1^2 & x_2^2 &x_3^2&...&x_n^2\\ ...&...&...&...&...\\ ...&...&...&...&x_n^{n-1}\\ x_1^n & x_2^n&x_3^n&...&x_n^n\\ \end{vmatrix}=\begin{vmatrix} 1 & 1 &1&...&1\\ x_1^1 & x_2^1 &x_3^1&...&x_n^1\\ x_1^2 & x_2^2 &x_3^2&...&x_n^2\\ ...&...&...&...&...\\ ...&...&...&...&x_n^{n-1}\\ x_1^n & x_2^n&x_3^n&...&x_n^n\\ \end{vmatrix} Dn= x10x11x12......x1nx20x21x22......x2nx30x31x32......x3n..................xn0xn1xn2...xnn−1xnn = 1x11x12......x1n1x21x22......x2n1x31x32......x3n..................1xn1xn2...xnn−1xnn
这样的行列式称为“范德蒙德行列式”
一般按照以下规则计算
D n = ∏ 1 < = i < j < = n ( x j − x i ) = − − − − − − − − − − − − − − − − − − − − − − − − − − − − ( x n − x n − 1 ) ( x n − x n − 2 ) . . . ( x n − x 1 ) ( x n − 1 − x n − 2 ) ( x n − 1 − x n − 3 ) . . . ( x n − 1 − x 1 ) . . . ( x 3 − x 2 ) ( x 3 − x 1 ) ( x 2 − x 1 ) D_n = \prod_{1<=i<j<=n}{(x_j-x_i)} = \\ ----------------------------\\ (x_n-x_{n-1})(x_n-x_{n-2})...(x_n-x_{1})\\(x_{n-1}-x_{n-2})(x_{n-1}-x_{n-3})...(x_{n-1}-x_{1})\\ ...\\ (x_{3}-x_{2})(x_{3}-x_{1})\\ (x_{2}-x_{1}) Dn=∏1<=i<j<=n(xj−xi)=−−−−−−−−−−−−−−−−−−−−−−−−−−−−(xn−xn−1)(xn−xn−2)...(xn−x1)(xn−1−xn−2)(xn−1−xn−3)...(xn−1−x1)...(x3−x2)(x3−x1)(x2−x1)
证明过程如下


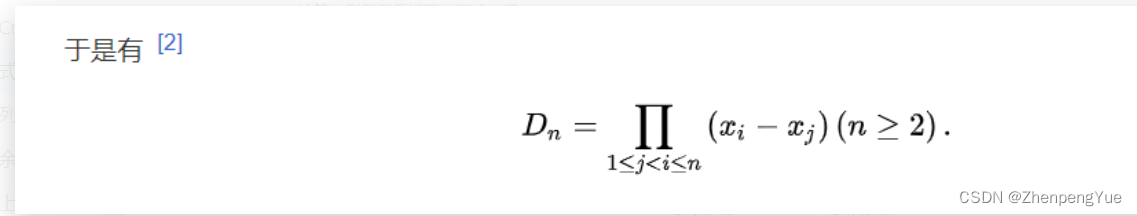
七、克莱姆法则(Cramer’s Rule)
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 . . . a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n \begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= b_1 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= b_2 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n= b_n \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3+...+a1nxn=b1a21x1+a22x2+a23x3+...+a2nxn=b2...an1x1+an2x2+an3x3+...+annxn=bn
对于这样一个方程组,我们定义一个行列式,只存它的系数,称为”系数行列式”
D n = ∣ a 11 a 12 a 13 . . . a 1 n a 21 a 22 a 23 . . . a 2 n a 31 a 32 a 33 . . . a 3 n . . . . . . . . . . . . . . . . . . . . . . . . . . . a ( n − 1 ) n a n 1 a n 2 . . . a n ( n − 1 ) a n n ∣ D_{n} =\begin{vmatrix} a_{11} & a_{12} &a_{13}&...&a_{1n}\\ a_{21} & a_{22}&a_{23}&...&a_{2n}\\ a_{31}&a_{32}&a_{33}&...&a_{3n}\\ ...&...&...&...&...\\ ...&...&...&...&a_{(n-1)n}\\ a_{n1}&a_{n2}&...&a_{n(n-1)}&a_{nn}\\ \end{vmatrix} Dn= a11a21a31......an1a12a22a32......an2a13a23a33........................an(n−1)a1na2na3n...a(n−1)nann
应用:克莱姆法则判断具有N个方程、N个未知数的线性方程组的解:
- 当方程组的系数行列式不等于零时,方程组且具有唯一解;
- 如果方程组无解或者有两个不同的解,方程组的系数行列式等于零
- 克莱姆法则不仅仅适用于实数域,它在任何域上面都成立。
克莱姆法则的局限性:
- 方程个数与未知数的个数不同时,系数的行列式等于零时,克莱姆法则失效。
- 运算量较大,求解一个N阶线性方程组要计算N+1个N阶行列式
相关文章:
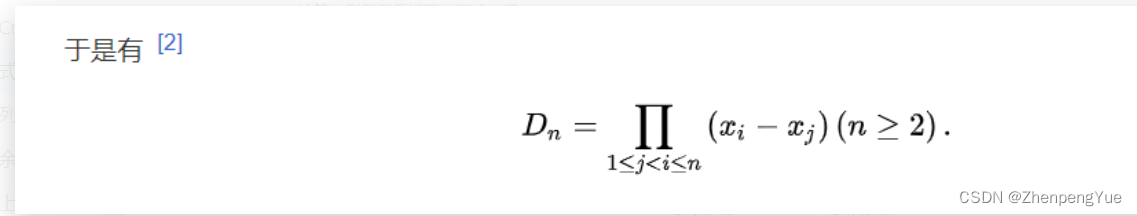
线性代数基础-行列式
一、行列式之前的概念 1.全排列: 把n个不同的元素排成一列,称为n个元素的全排列,简称排列 (实际上就是我们所说的排列组合,符号是A,arrange) 2.标准序列: 前一项均小于后一项的序列…...
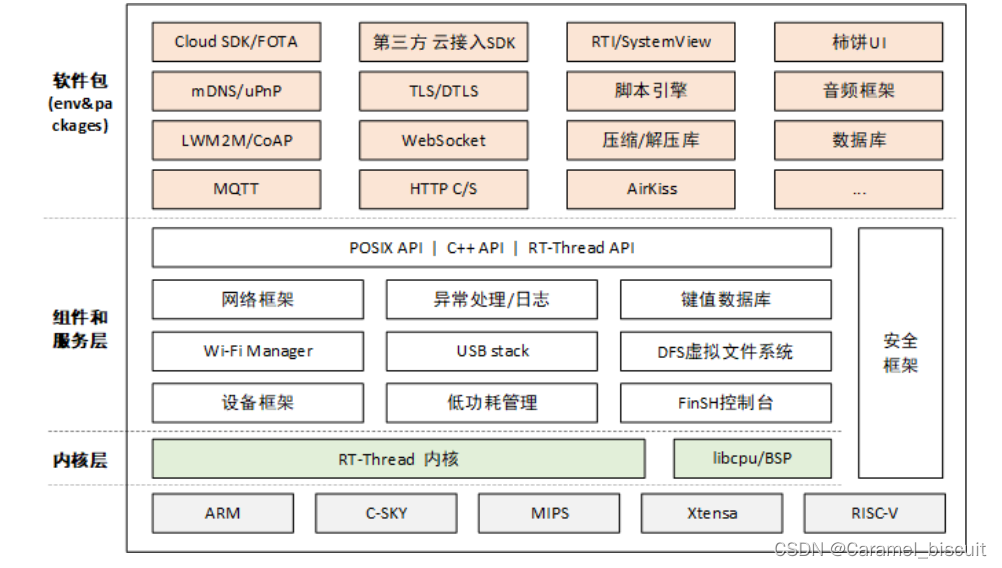
RT-Thread(学习)
RT-Thread是一款完全由国内团队开发维护的嵌入式实时操作系统(RTOS),具有完全的自主知识产权。经过16个年头的沉淀,伴随着物联网的兴起,它正演变成一个功能强大、组件丰富的物联网操作系统。 RT-Thread概述 RT-Threa…...

【MySQL】 MySQL 死锁问题分析优化器特性及优化方案
MySQL 死锁问题分析优化器特性及解决方案 MySQL 锁机制介绍 1、MySQL常用存储引擎的锁机制 MyISAM和MEMORY采用表级锁(table-level locking) BDB采用页面锁(page-level locking)或表级锁,默认为页面锁 InnoDB支持行级锁(row-level locking)和表级锁,默认为行级…...
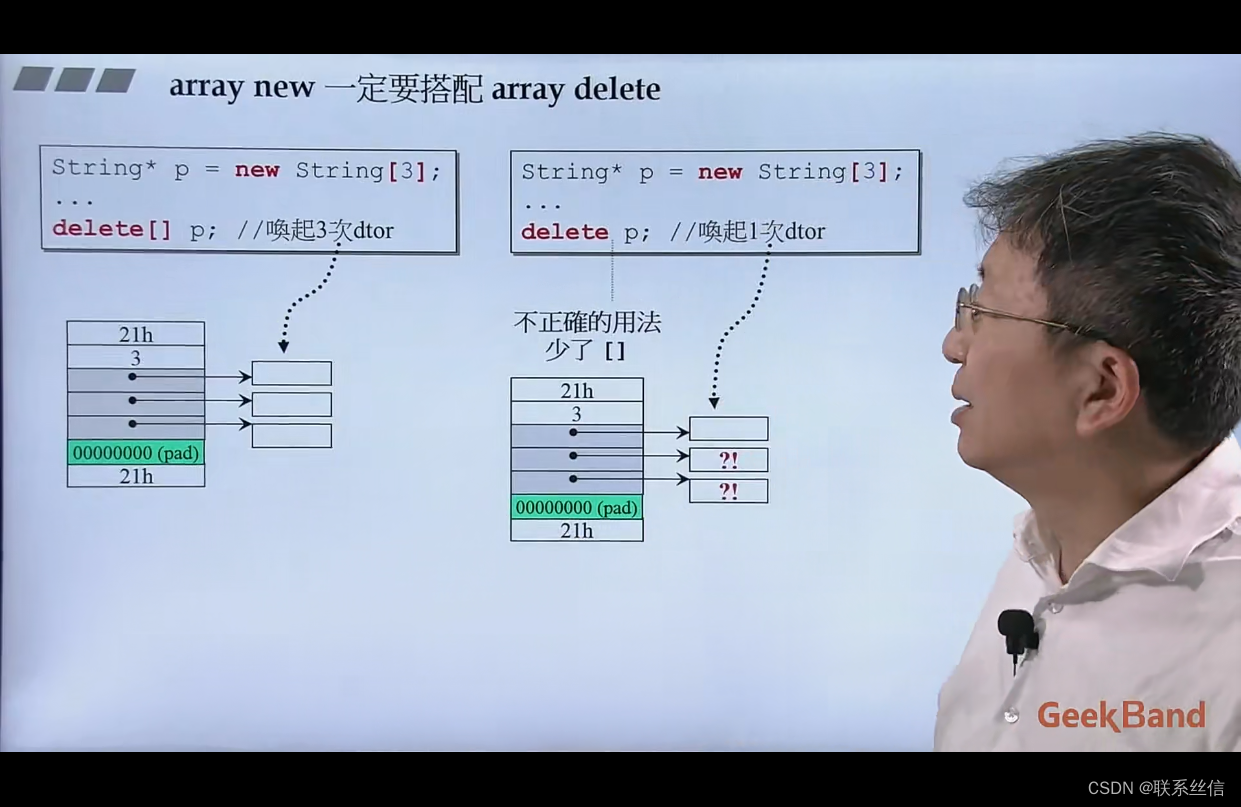
【C++面向对象侯捷】8.栈,堆和内存管理
文章目录 栈,堆stack object的生命周期static local object的生命周期global object的生命周期heap objects 的生命期new:先分配memory,再调用构造函数delete: 先调用析构函数,再释放 memory动态分配所得的内存块,in V…...

在比特币上使用可检索性证明支付存储费用
我们为用户开发了一种为云存储付费的新方法。 与亚马逊的 S3 等传统云存储相比,用户不必信任服务器。 我们使用比特币智能合约来确保支付取决于服务器的可检索性证明 (PoR),该证明只能在数据仍然可用且需要时可以检索的情况下生成。 可检索性证明 (PoR)…...
实现服务端给客户端发消息)
使用SSE(Server-Sent Events)实现服务端给客户端发消息
首先是客户端,看着比较简单。但实际应用中可能要比这复杂,因为默认sse只支持get请求,而且没法携带header。所以如果默认的方法达不到需求的话可能需要额外实现,当然也可以引用第三方库,比如rangermauve/fetch-event-so…...

【Redis】使用rpm包安装redis
背景说明 公司环境处于内网,某同事需要安装redis,如果使用通过源码编译安装redis,很多编译工具如gcc就需要先安装,但处于内网安装起来不太方便,当然也不是不可以。我们此处就选用通过redis的rpm包进行安装。 rpm包查…...
论文阅读-Group-based Fraud Detection Network on e-Commerce Platforms
目录 摘要 1 Introduction 2 BACKGROUND AND RELATED WORK 2.1 Preliminaries 2.2 Related Works 3 MODEL 3.1 Structural Feature Initialization 3.2 Fraudster Community Detection 3.3 Training Objective 4 EXPERIMENT 4.1 Experimental Setup 4.2 Prediction …...
java程序启动时指定JVM内存参数和Xms、Xmx参数学习
先找个java程序来试验;找这个, java实现计算机图形学中点画线算法_java 多个点连成一条线 算法-CSDN博客 JVM内存参数中, -Xms:设置堆内存的初始大小,默认为物理内存的1/64; -Xmx:设置堆内存的…...

【C++编程能力提升】
代码随想录训练营Day44 | Leetcode 518、377 一、完全背包问题1、完全背包与01背包的区别 二、518 零钱兑换II三、377 组合总和IV 一、完全背包问题 1、完全背包与01背包的区别 第一,物品的有限与无限; 01背包:物品是有限的。(每…...

FlashDuty Changelog 2023-09-21 | 自定义字段和开发者中心
FlashDuty:一站式告警响应平台,前往此地址免费体验! 自定义字段 FlashDuty 已支持接入大部分常见的告警系统,我们将推送内容中的大部分信息放到了 Lables 进行展示。尽管如此,我们用户还是会有一些扩展或定制性的需求…...
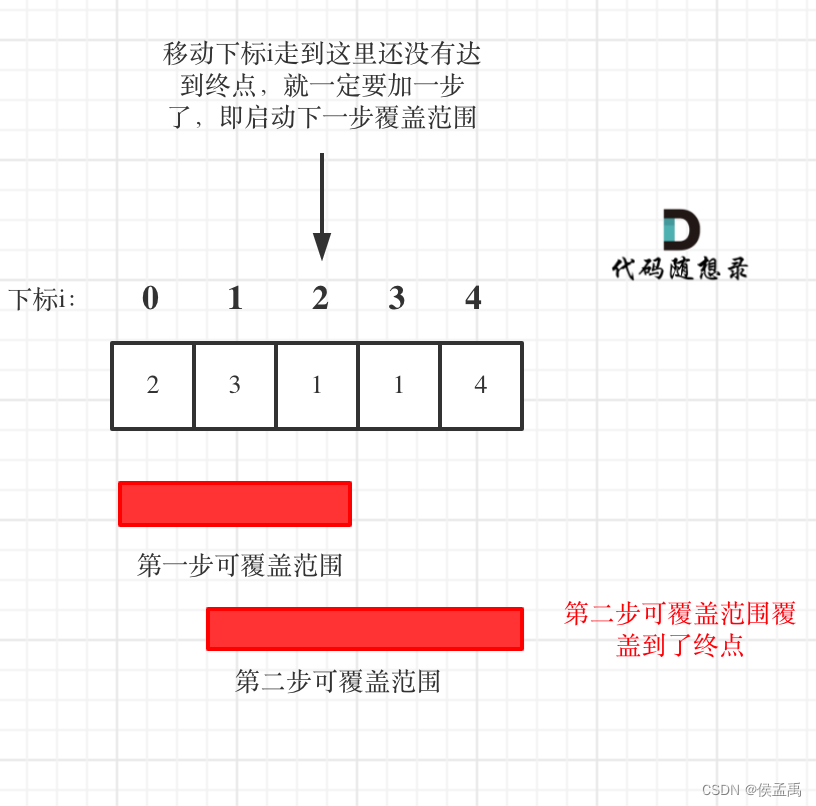
贪心算法-
代码随想录 什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 这么说有点抽象,来举一个例子: 例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿ÿ…...
漫谈:C语言 C++ 左值、右值、类型转换
编程不是自然语言,编程自有其内在逻辑。 左值引起的BUG 编译器经常给出类似这样的BUG提示: “表达式必须是可修改的左值” “非常量引用的初始值必须是左值” 看一下示例: #include <iostream>void f(int& x) {} int main() {sho…...

前车之鉴,后车之师
问题分类具体解释可能导致的后果解决方法备注主从延迟数据库写后立即读的场景,比如订单落地成功抛消息,消息接收方再读订单推订单中心、发触达、落地数据等场景,再读数据时走从库,可能读不到数据。脏数据业务逻辑有问题延迟消费。…...

WEB使用VUE3实现地图导航跳转
我们在用手机查看网页时可以通过传入经纬度去设置目的地然后跳转到对应的地图导航软件,如果没有下载软件则会跳转到下载界面 注意: 高德地图是一定会跳转到一个新网页然后去询问用户是否需要打开软件百度和腾讯地图是直接调用软件的这个方法有缺陷&…...

今天聊一聊高性能系统架构设计是什么样的
Java全能学习面试指南:https://javaxiaobear.cn 今天聊一聊大家常听到的高性能系统架构。 高性能系统架构,主要包括两部分内容,性能测试与性能优化。性能优化又可以细分为硬件优化、中间件优化、架构优化及代码优化,知识架构图如…...
鼠标不动了怎么办?3招解决问题!
“这是怎么回事呢?我的鼠标怎么会用着用着就突然不动了呢?现在有一些比较重要的工作要处理。请问有什么方法可以快速解决这个问题吗?” 随着电脑在我们日常生活和工作中的广泛应用,鼠标是我们操作电脑不可或缺的工具之一。但是&am…...

2023-09-23力扣每日一题
链接: 1993. 树上的操作 题意 **Lock:**指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。**Unlock:**指定用户给指定节点 解锁 ,只有当…...
C#中使用Newtonsoft.Charp实现Json对象序列化与反序列化
场景 C#中使用Newtonsoft.Json实现对Json字符串的解析: C#中使用Newtonsoft.Json实现对Json字符串的解析_霸道流氓气质的博客-CSDN博客 上面讲的对JSON字符串进行解析,实际就是JSON对象的反序列化。 在与第三方进行交互时常需要封装对象,…...

Golang开发--互斥锁和读写锁
互斥锁(Mutex) 互斥锁(Mutex)是一种并发控制机制,用于保护共享资源的访问。互斥锁用于确保在任何给定时间只有一个 goroutine(Go 语言中的并发执行单元)可以访问被保护的共享资源,从…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
