n个骰子掷出m点的概率,C++实现
一.在骰子游戏中,我们会有猜点数的问题。我们该如何用算法来描述呢?
加入我们当前只有一个骰子,我们该如何算概率呢?
我们现在开始推导一下吧:
首先是一个骰子的情况,我们可以简单的知道n个骰子一共可以掷出6^n种排列组合
一个骰子的情况:1 1 1 1 1 1
两个骰子的情况:0 1 2 3 4 5 6 5 4 3 2 1
三个骰子的情况:0 0 1 3 6 10....
此时我们的到了一个递推公式:
dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1][j-3]+dp[i-1][j-4]+dp[i-1][j-5]+dp[i-1][j-6];(i-6>0);
二.我们来处理一下代码逻辑
int main() {int n=5;int m=30;vector<vector<int>> res(n,vector<int>(m));for(int i=0;i<6;i++) res[0][i]=1;for(int i=1;i<n;i++){for(int j=i;j<m&&j<6*(i+1);j++){int temp=0;for(int k=1;k<=6;k++)if(k<=j) {temp += res[i - 1][j - k];}res[i][j]=temp;}}
}我在此处代码的写法是写死的,最后的概率是res[n-1][m-1]/6^n.在输入的时候也得判断m所处的区间必须是n~6^n,大家自己加一下啊。
三.拓展
这里也可以拓展成为扑克排的算点数的问题,可以封装成一个类,之后使用的时候,只需要新建类就可以了。
相关文章:

n个骰子掷出m点的概率,C++实现
一.在骰子游戏中,我们会有猜点数的问题。我们该如何用算法来描述呢? 加入我们当前只有一个骰子,我们该如何算概率呢? 我们现在开始推导一下吧: 首先是一个骰子的情况,我们可以简单的知道n个骰子一共可以掷出…...
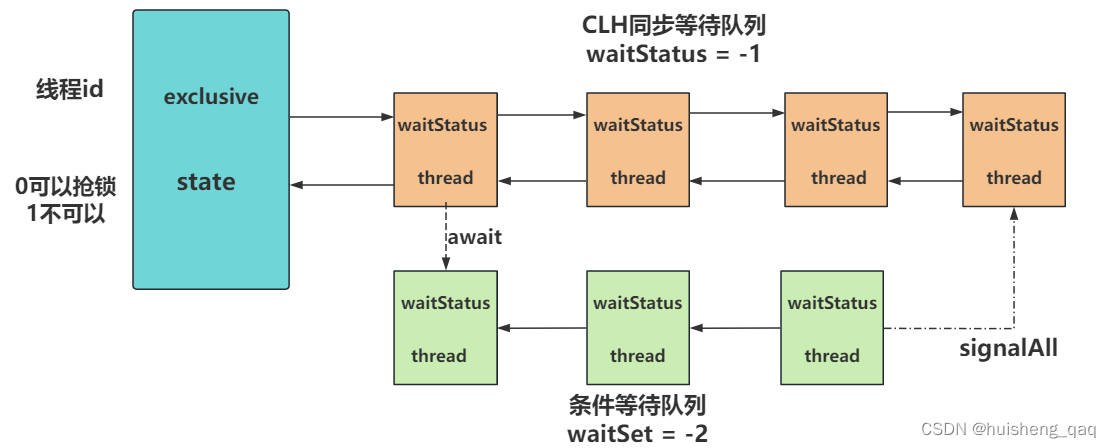
【JUC系列-08】深入理解CyclicBarrier底层原理和基本使用
JUC系列整体栏目 内容链接地址【一】深入理解JMM内存模型的底层实现原理https://zhenghuisheng.blog.csdn.net/article/details/132400429【二】深入理解CAS底层原理和基本使用https://blog.csdn.net/zhenghuishengq/article/details/132478786【三】熟练掌握Atomic原子系列基本…...
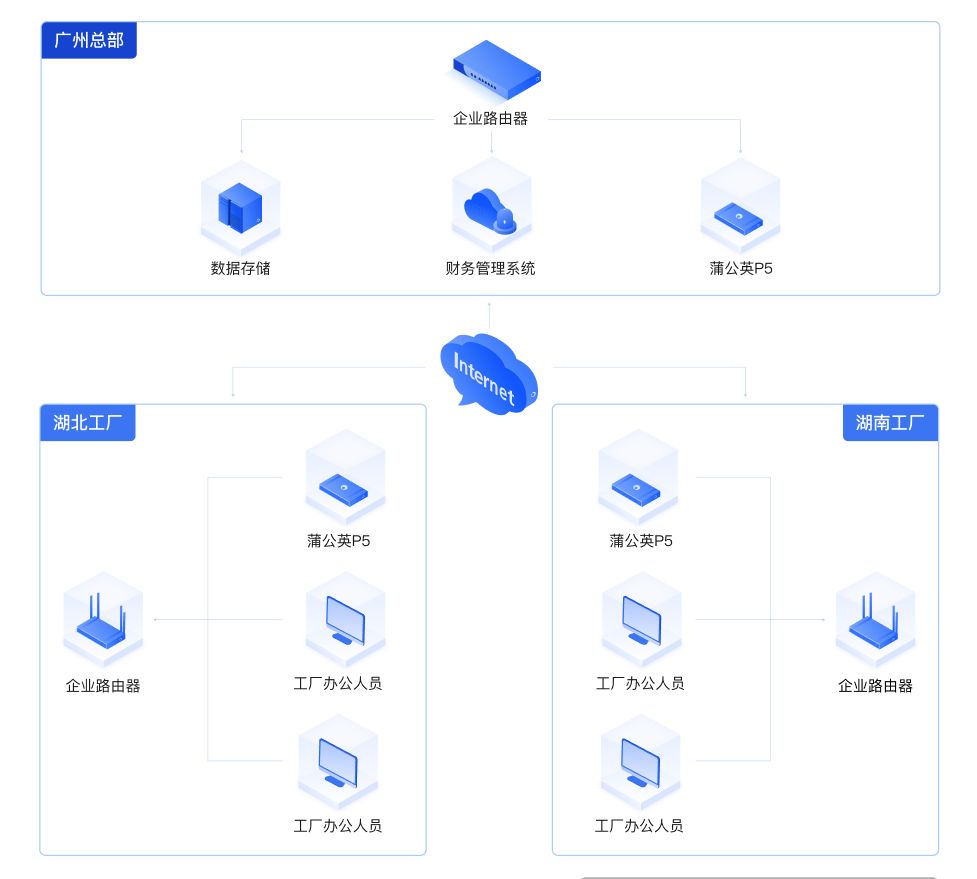
企业专线成本高?贝锐蒲公英轻松实现财务系统远程访问
在办公及信息系统领域,许多企业纷纷采用金蝶等财务管理软件来提升运营效率。以某食品制造企业为例,该企业总部位于广州,并拥有湖北仙桃工厂、广州从化工厂和湖南平江工厂三大生产基地。为提高管理效率,该企业在广州总部局域网内部…...

自学——网络安全——黑客技术
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客!!! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队…...
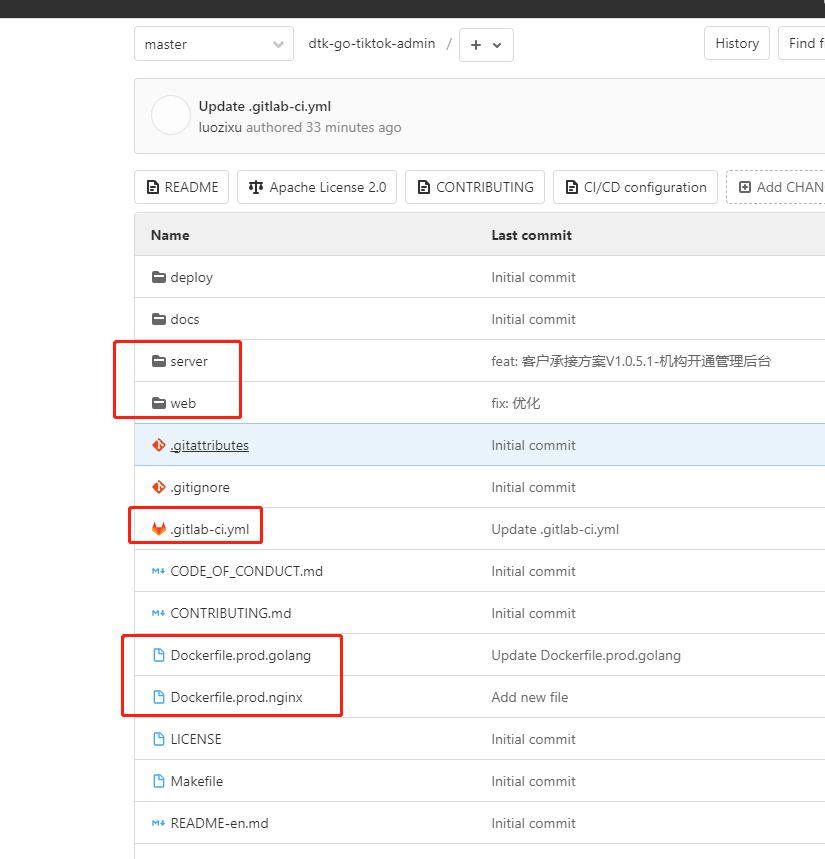
k8s部署gin-vue-admin框架、gitlab-ci、jenkins pipeline 、CICD
测试环境使用的jenkins 正式环境使用的gitlab-ci 测试环境 创建yaml文件 apiVersion: v1 kind: ConfigMap metadata:name: dtk-go-tiktok-admin-configlabels:app.kubernetes.io/name: dtk-go-tiktok-adminapp.kubernetes.io/business: infrastructureapp.kubernetes.io/run…...
【SpringBoot项目】SpringBoot+MyBatis+MySQL电脑商城
在b站听了袁老师的开发课,做了一点笔记。 01-项目环境搭建_哔哩哔哩_bilibili 基于springboot框架的电脑商城项目(一)_springboot商城项目_失重外太空.的博客-CSDN博客 项目环境搭建 1.项目分析 1.项目功能:登录、注册、热销…...
互联网医院|互联网医院系统引领医疗科技新风潮
互联网的迅速发展已经改变了人们的生活方式,而医疗领域也不例外。近年来,互联网医院应运而生,为患者和医生提供了更便捷、高效的医疗服务。本文将深入探讨互联网医院的系统特点、功能以及未来的发展方向,为您展现医疗行业的新时代…...

Mock安装及应用
1、安装 npm install mockjs 2、Mock.Random属性 该属性是一个工具类,用于生成各种随机数据。它提供的方法如下: Basic: boolean,natural,integer,float,character,string,range,date,time,datetime,now; Image: image,dataImage; Color: color; Text: p…...

一起来看看UI设计流程详解吧!通俗易懂
UI设计2023 通俗易懂的UI设计流程详解 首先,大家要明确一下范围:一般分为新产品的从0-1和已有产品上新的模块或功能的从0-1,这两个方向的环节和产出物会有比较大的区别。其实在UI设计师介入之前,我们是需要去了解一些大的方向和…...

TikTok营销成功秘籍:ROI指标的黄金法则
在当今数字营销领域,TikTok已经崭露头角,成为了品牌和营销者们争相追逐的热门平台。 然而,要在TikTok上取得成功,不仅需要创意和内容,还需要精确的ROI(投资回报率)指标来衡量和优化你的营销策略…...
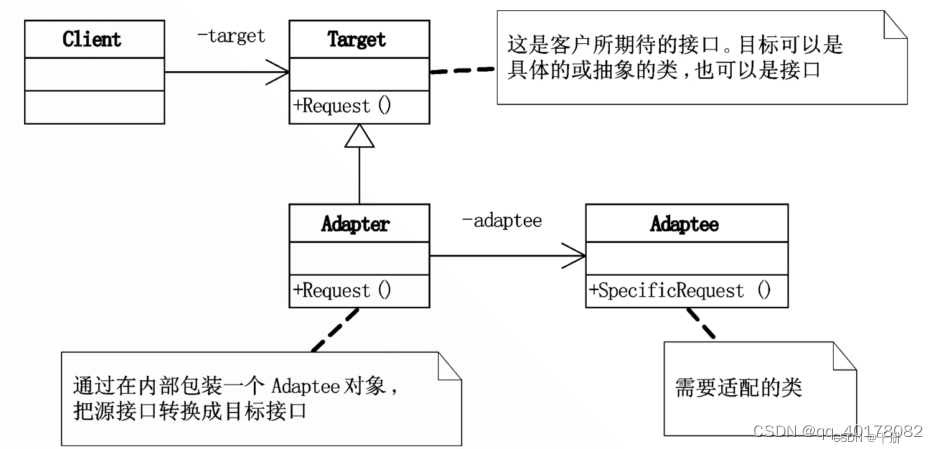
17.适配器模式(Adapter)
意图:将一个类的接口转换为Client希望的另一个接口,使得原本由于接口不兼容而不能一起工作的那些类在一起工作。 UML图 Target:定义Client使用的与特定领域相关的接口。 Client:与符合Target接口的对象协同工作。 Adaptee…...

leetcode做题笔记154. 寻找旋转排序数组中的最小值 II
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4]若旋转 7 次࿰…...
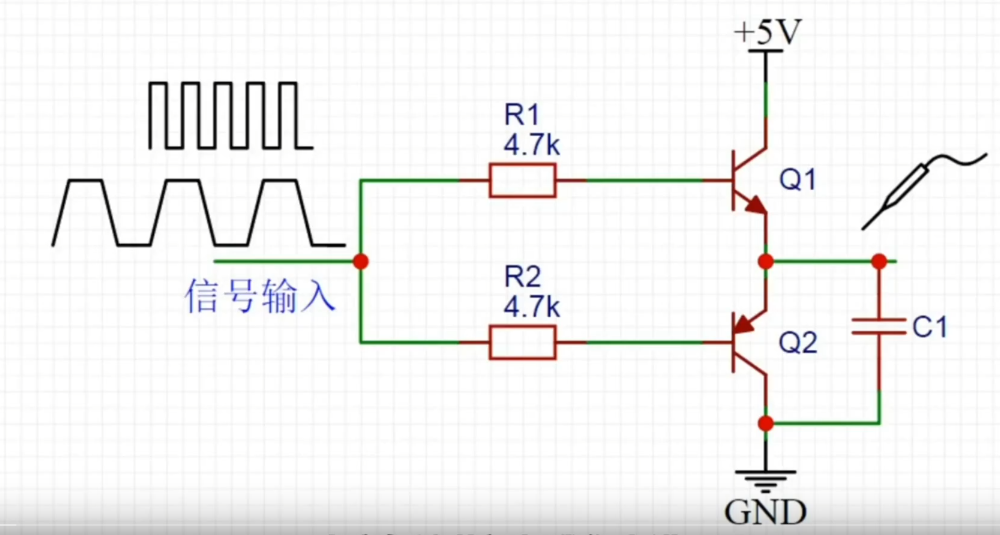
什么是推挽电路?
推挽电路原理: 可以简单理解为推和拉; 此电路总共用到两个元器件,对应图中的Q1----NPN三极管,Q2----PNP三极管,两个电阻R1和R2起到限流的作用;两个三极管的中间对应信号的输出。 下面就举例说明是如何工作的…...
:窗口的使用,处理函数的使用)
208.Flink(三):窗口的使用,处理函数的使用
目录 一、窗口 1.窗口的概念 2.窗口的分类 (1)按照驱动类型分 (2)按照窗口分配数据的规则分类 3.窗口api概览 (1)按键分区(Keyed)和非按键分区(Non-Keyed) *1)按键分区窗口(Keyed Windows) *2)非按键分区(Non-Keyed Windows) (2)代码中窗口API的调…...

时序预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络时间序列预测
时序预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络时间序列预测 目录 时序预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现POA-CNN-BiLSTM鹈鹕算…...

【知识点】增量学习、在线学习、离线学习的区别
参考链接:https://www.6aiq.com/article/1613258706447?p1&m0 离线学习 常见的学习方式,一次性将所有数据参与进训练。 离线学习完成了目标函数的优化将不会在改变了离线学习需要一次提供整个训练集时间和空间成本效率低发生数据变更或模型漂移需…...

c++ 学习 之 运算符重载 之 前置++和后置++
前言 int a1;cout << (a) << endl;cout << a << endl;int b1;cout << (b) << endl; // 这个是错误的cout << b << endl;上面样例中, 前置 返回的是引用,所以a 的值变成了3 后置 返回的不是可以改变的…...

K8s Kubelet 垃圾回收机制
前言 Kubelet 垃圾回收(Garbage Collection)是一个非常有用的功能,它负责自动清理节点上的无用镜像和容器。Kubelet 每隔 1 分钟进行一次容器清理,每隔 5 分钟进行一次镜像清理(截止到 v1.15 版本,垃圾回收间隔时间还都是在源码中固化的,不可自定义配置)。如果节点上已…...
docker安装高斯数据库openGauss数据库
1.创建容器 #创建数据没有挂在的容器 docker run --name opengauss --privilegedtrue -d -e GS_PASSWORDEnmo123 -p 8090:5432 enmotech/opengauss:latest 2. 进入容器,并切换omm用户,使用gsql连接高斯数据库 [rootansible ~]# docker ps -a CONTAIN…...

新手学习:ArcGIS 提取SHP 路网数据、节点
新手学习:ArcGIS 提取SHP 路网数据、节点 参考连接 OSM路网提取道路节点 ArcGIS:如何创建地理数据库、创建要素类数据集、导入要素类、表? 1. 导入开源路网SHP文件 2. 在交点处打断路网数据 未打断路网数据 有一些路径很长,…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...
