队列的使用以及模拟实现(C++版本)
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:讲解队列的使用以及模拟实现
金句分享:
✨来日方长,未来是星辰大海般璀璨,✨
✨不必踌躇于过去的半亩方塘.✨
目录
- 一、队列的介绍
- 二、队列的使用
- 🍭练练手(用队列模拟栈)
- 三、队列的模拟实现:
- (1) 浅提一下双端队列`deque`
- (2) 模拟实现
一、队列的介绍
C++中的队列是一种容器,使用队列可以实现先进先出(FIFO)的数据结构。队列可以添加元素到队列的末尾,也可以从队列的开头删除元素。
队列作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的
成员函数来访问其元素。元素从队尾入队列,从队头出队列。
C++中的队列通常使用STL库中的queue类实现。
队列的基本操作包括:
- push(element):将元素插入队列的末尾。
- pop():将队列的第一个元素删除。
- front():返回队列的第一个元素。
- back():返回队列的最后一个元素。
- empty():判断队列是否为空。
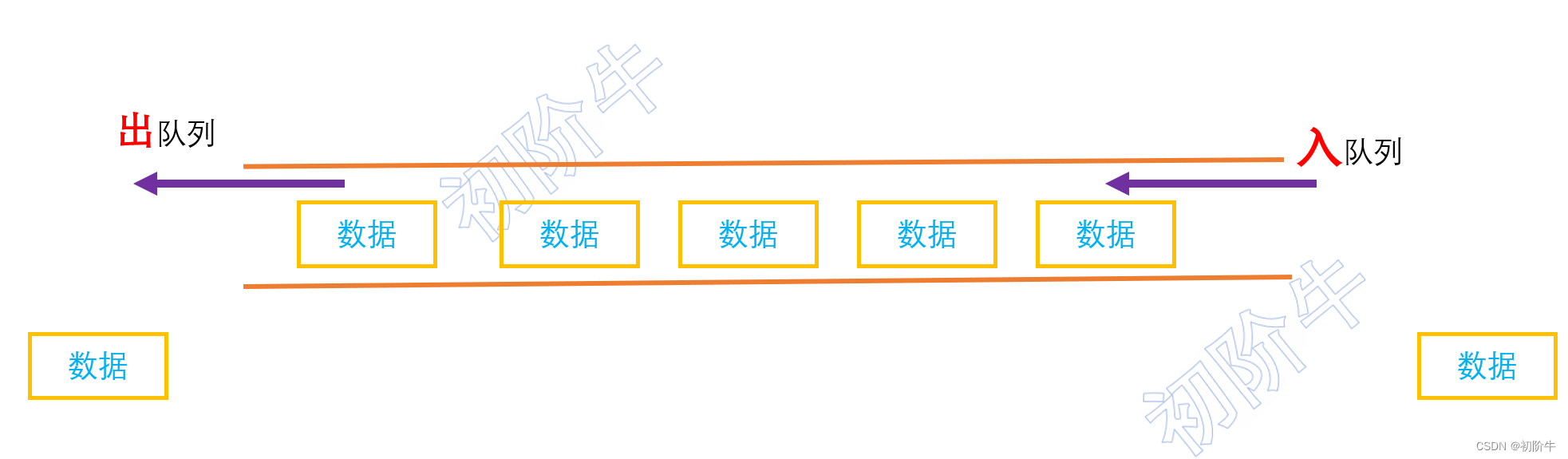
队列具有先进先出FIFO(First In First Out)
入队列:进行"插入"操作的一端称为队尾
出队列:进行"删除"操作的一端称为队头
二、队列的使用
文档链接

| 接口名 | 解释 |
|---|---|
| empty() | 判断是否为空队列 |
| size() | 返回队列中有效元素的个数 |
| front() | 返回队首元素的引用 |
| back() | 返回队尾元素的引用 |
| push() | 将新元素入队列 |
| emplace() | 将新元素入队列 |
| pop() | 将队首元素出队 |
相信大家对队列的基本操作十分简单,下面演示一下具体使用,使用十分简单,就不过分介绍了.
测试代码:
#include <iostream>
#include <queue>
using namespace std;void test1()
{queue<int> q1;//创建一个存储整形数据的队列q1.push(1); //入队列q1.push(2);q1.push(3);q1.emplace(4); //在stack使用时有详细介绍cout << "q1.front=" << q1.front() << endl; //取队头元素cout << "q1.back=" << q1.back() << endl; //取队尾元素//利用front的返回值,修改队首元素int& top = q1.front();top = 22;//利用back的返回值,修改队尾元素int& back = q1.back();top = -22;cout << endl;while (!q1.empty()) //只要队列不为空,就打印队头元素和出队列{cout << q1.front() << endl;q1.pop();//出队列}
}int main()
{test1();return 0;
}
运行结果:
q1.front=1
q1.back=4
22
2
3
4
🍭练练手(用队列模拟栈)
题目链接:
同样,在C语言阶段,我们已经"十分痛苦"的写过这道题,现在C++阶段,再来写要轻松很多了.
用队列实现栈(C语言版本)
C++实现版本:
class MyStack {
public:MyStack() {}void push(int x) {if (!(q1.empty() && q2.empty())) {//往空栈里面插入数据q1.push(x);}else q2.push(x);}int pop() {queue<int>* empty_q ;queue<int>* un_empty_q;if (q1.empty()) {//找到两个队列中的空队列empty_q = &q1;un_empty_q = &q2;}else {empty_q = &q2;un_empty_q = &q1;}while (un_empty_q->size() > 1) {//将非空队列除了最后一个元素以外,其他全部插入到另一个队列empty_q->push(un_empty_q->front());un_empty_q->pop();}int front = un_empty_q->front();un_empty_q->pop();//删除剩下的最后一个元素->return front;}int top() {int top;if (q1.empty()) {top = q2.back();}else top = q1.back();return top;}bool empty() {return q1.empty() && q2.empty();}
private:queue<int> q1;queue<int> q2;
};
三、队列的模拟实现:
(1) 浅提一下双端队列deque
在介绍队列的,模拟实现前,先介绍一下deque.
双端队列(Double-Ended Queue),是一种具有队列和栈的特点的数据结构。它允许从两端插入和删除元素,具有以下特点:
- 可以从队列两端进行插入和删除操作。
- 支持常数级别的访问和修改元素,即在队列头和尾进行操作的时间复杂度都为O(1)。
- 在中间进行操作时,性能较差,时间复杂度为O(n)。
是的,这个双端队列不仅支持头插头删,尾插尾删的同时,还支持随机访问.
那这不就意味着链表list和vector都被淘汰了吗?
这里就不过多介绍deque的底层了,我们可以暂时理解为,类似于链表,但是链接起来的是一个个数组,这样就实现了这些功能.
但是,他并不能代替链表list和vector.原因如下:
与vector比较
deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不
需要搬移大量的元素
劣势:但是它的访问需要计算,在大量访问元素的场景时,与vector比就落后了.
与list比较
优势:其底层是连续空间,空间利用率比较高,不需要存储额外字段。
缺点:deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多.
巧合的是,stack和queue都不需要访问中间的元素,访问头部数据效率还是很高的.
所以STL用deque作为stack和queue的底层数据结构再合适不过了.
(2) 模拟实现
队列也是一种容器适配器,我们底层采用deque实现还是很轻松的.

#pragma once
#include <iostream>
#include <deque>
using namespace std;namespace cjn
{template<class T, class Con = deque<T>>//默认采用deque进行复用class queue{public:queue(){}void push(const T& x){ //入队列元素相当于尾插_c.push_back(x);}void pop(){_c.pop_front(); //出队列是从队首元素出队,所以相当于头删}T& back(){ //返回队尾元素return _c.back();}const T& back()const{return _c.back();}T& front(){ //返回队首元素return _c.front();}const T& front()const{return _c.front();}size_t size()const{ //返回队列中有效元素的个数return _c.size();}bool empty()const{ //判断队列是否为空return _c.empty();}private:Con _c;};
}
相关文章:

队列的使用以及模拟实现(C++版本)
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻强烈推荐优质专栏: 🍔🍟🌯C的世界(持续更新中) 🐻推荐专栏1: 🍔🍟🌯C语言初阶 🐻推荐专栏2: 🍔…...
RV1126笔记四十一:RV1126移植LIVE555
若该文为原创文章,转载请注明原文出处。 RV1126的SDK有提供了一个librtsp.a封装好的RTSP推流库,但不开源,还有个确定延时长,所以想自己写一个RTSP的推流,但不想太麻烦,所以使用Live555。 记录下移植过程和测试结果。 live555需要用到的包有 openssl 和live555 一、 编…...
stable diffusion模型评价框架
GhostReview:全球第一套AI绘画ckpt评测框架代码 - 知乎大家好,我是_GhostInShell_,是全球AI绘画模型网站Civitai的All Time Highest Rated (全球历史最高评价) 第二名的GhostMix的作者。在上一篇文章,我主要探讨自己关于ckpt的发展方向的观点…...
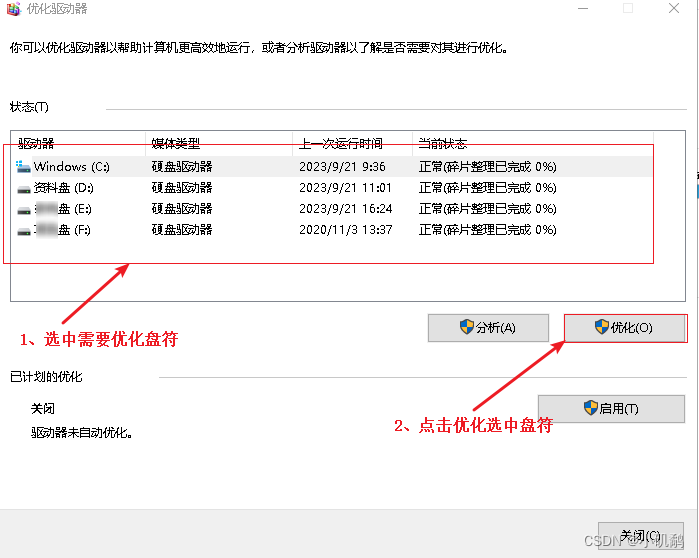
电脑开机慢问题的简单处理
电脑用久了,开机时间要10-20分钟特别慢,一下介绍两种简单有效处理方式,这两种方式经测试不会影响原系统软件的使用: 方式一:禁用非必要启动项【效果不是很明显】 利用360里面的优化加速禁用启动项【禁用启动项还有其…...

SpringMVC-Rest风格
一、简介 REST(Representational State Transfer),表现形式状态转换,它是一种软件架构风格 当我们想表示一个网络资源的时候,可以使用两种方式: 传统风格资源描述形式 http://localhost/user/getById?id1 查询id为1的用户信息…...

WebGL实现透明物体(α混合)
目录 α混合 如何实现α混合 1. 开启混合功能: 2. 指定混合函数 混合函数 gl.blendFunc()函数规范 可以指定给src_factor和dst_factor的常量 混合后颜色的计算公式 加法混合 半透明的三角形(LookAtBlendedTriangl…...

RecycleView刷新功能
RecycleView刷新某一个Item,或这某一个Item中某一个View。 这样的需求,在实际的开发中是很普遍的。 在数据变化后需要刷新列表。 刷新列表有三种方式: 前两种大家应该很熟,第三中会有点陌生。 那么这三种方式,有什…...
目标检测如何演变:从区域提议和 Haar 级联到零样本技术
目录 一、说明 二、目标检测路线图 2.1 路线图(一般) 2.2 路线图(更传统的方法) 2.3 路线图(深度学习方法) 2.4 对象检测指标的改进 三、传统检测方法 3.1 维奥拉-琼斯探测器 (2001) 3.2 HOG探测器…...

聊一聊国内大模型公司,大模型面试心得、经验、感受
有着过硬的技术却无处可用是不是很苦恼呢,大家在面试时是不是也积累了一些经验呢,本文详细总结了大佬在大模型面试时的一些经验及感悟,希望对大家面试找工作有所帮助。 2023年,大模型突然国内火了起来,笔者就面了一些…...

【分布式微服务】feign 异步调用获取不到ServletRequestAttributes
公司调用接口的时候使用feign,但是服务之间还是使用了鉴权,需要通过RequestInterceptor 去传递uuid 概念 OpenFeign是一个声明式的Web服务客户端,它使得编写HTTP客户端变得更简单。在使用OpenFeign进行异步调用时,你可以通过配置来实现。但是,如果你在配置或调用过程中遇…...

c#编程里面最复杂的技术问题有哪些
C#编程中最复杂的技术问题通常涉及高级主题和复杂的应用场景。以下是一些可能被认为是C#编程中最复杂的技术问题: 1. **多线程和并发编程:** 处理多线程和并发问题涉及到锁定、线程同步、死锁避免、线程安全性和性能优化等方面的知识。编写高效且线程安…...
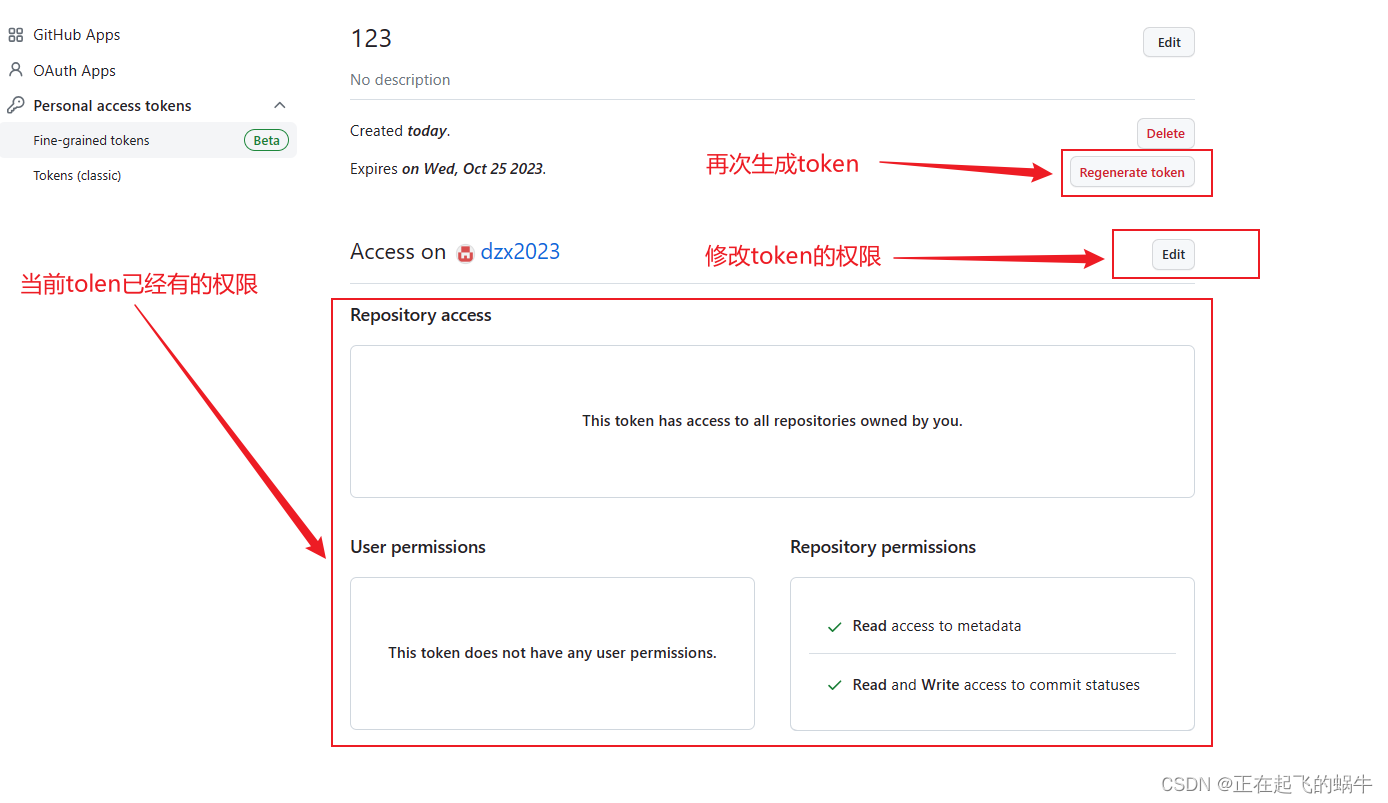
github代码提交过程详细介绍
1、下载github上面的代码 (1)在github网站上,找到想要下载的代码仓库界面,点击Code选项就可以看到仓库的git下载地址; (2)使用命令下载:git clone 地址; 2、配置本地git…...
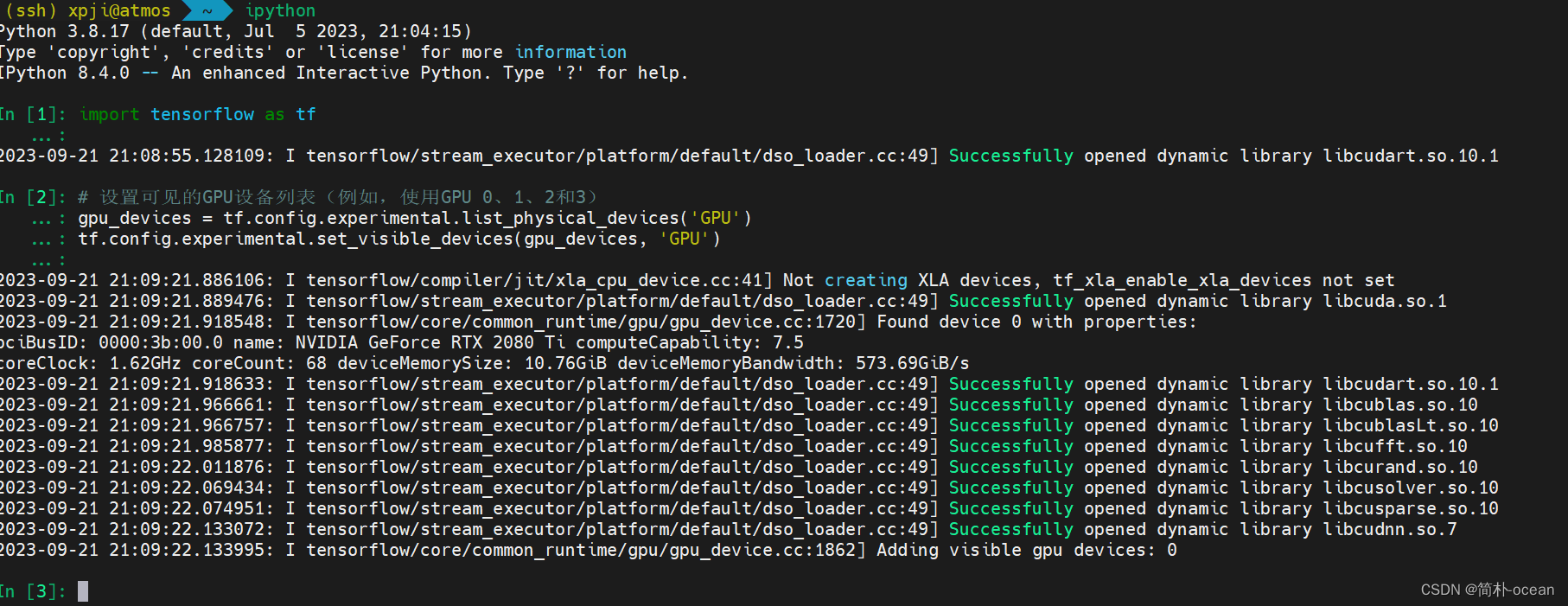
Linux -- 使用多张gpu卡进行深度学习任务(以tensorflow为例)
在linux系统上进行多gpu卡的深度学习任务 确保已安装最新的 TensorFlow GPU 版本。 import tensorflow as tf print("Num GPUs Available: ", len(tf.config.list_physical_devices(GPU)))1、确保你已经正确安装了tensorflow和相关的GPU驱动,这里可以通…...
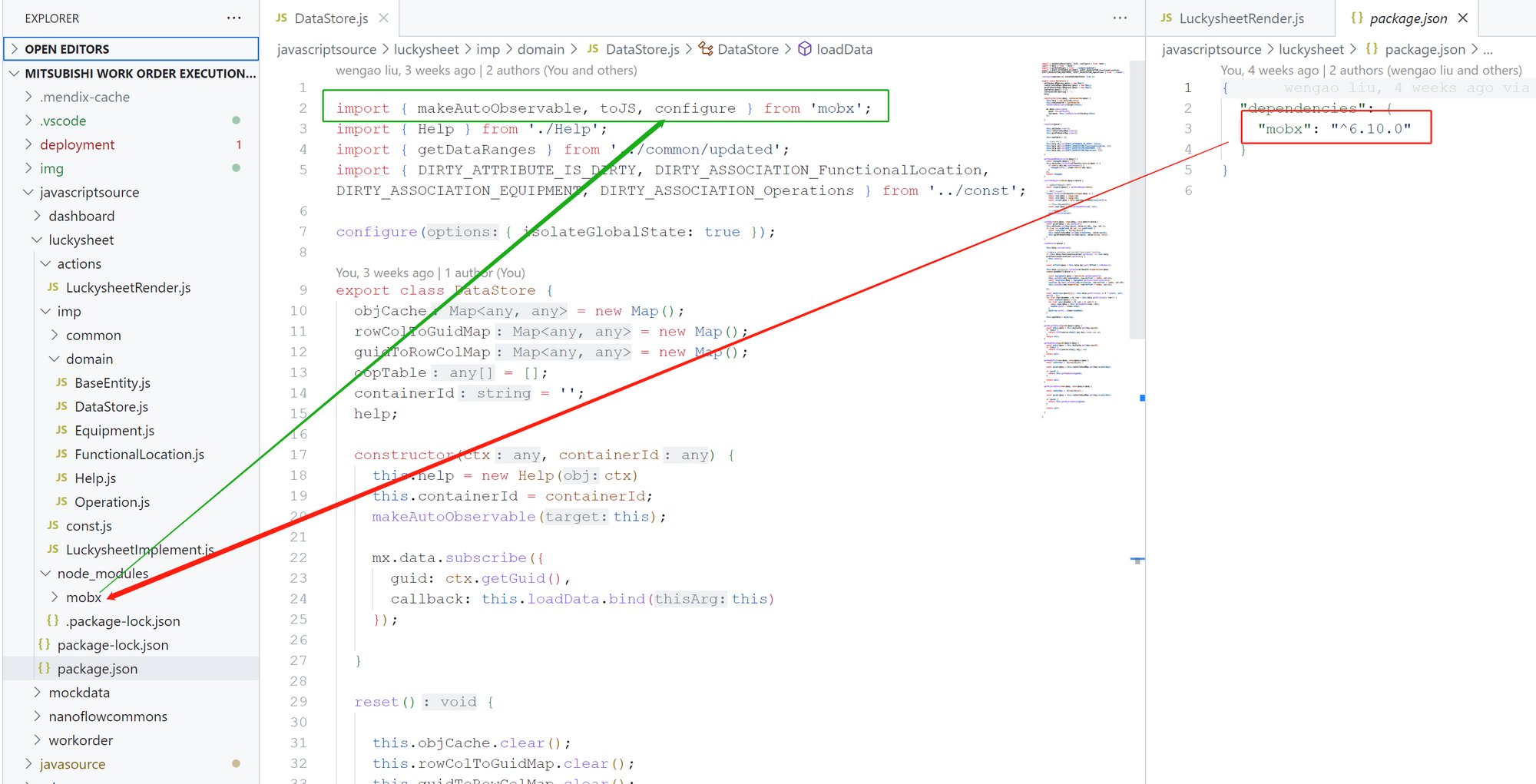
Mendix中的依赖管理:npm和Maven的应用
序言 在传统java开发项目中,我们可以利用maven来管理jar包依赖,但在mendix项目开发Custom Java Action时,由于目录结构有一些差异,我们需要自行配置。同样的,在mendix项目开发Custom JavaScript Action时,…...

自定义hooks之useLastState、useSafeState
自定义hooks之useLastState、useSafeState useLastState 在某些情况下,可能需要知道状态的历史值,例如,希望在状态变化时执行某些操作,但又需要访问上一个状态的值,以便进行比较或其他操作。自定义 React Hook 可以帮…...

前端判断: []+[], []+{}, {}+[], {}+{}
本质: 二元操作符规则 一般判断规则: 如果操作数是对象,则对象会转换为原始值如果其中一个操作数是字符串的话,另一个操作数也会转换成字符串,进行字符串拼接否则,两个操作数都将转换成数字或NaN,进行加法操作 转为原始数据类型的值的方法: Symbol.ToPrimitiveObject.protot…...
)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位) 我把封装指令的代码放在了main.js,代码如下 // 金额展示千分位 Vue.directive("thousands", {inserted: function(el, binding) {// debugger// 获取input节点if (el.tagName.toLocaleUppe…...

一篇博客学会系列(2)—— C语言中的自定义类型 :结构体、位段、枚举、联合体
目录 前言 1、结构体 1.1、结构体类型的声明 1.2、特殊的结构体类型声明 1.3、结构体的自引用 1.4、结构体的定义和初始化 1.5、结构体成员变量的调用 1.6、结构体内存对齐 1.6.1、offsetof 1.6.2、结构体大小的计算 1.6.3、为什么存在内存对齐? 1.7、…...
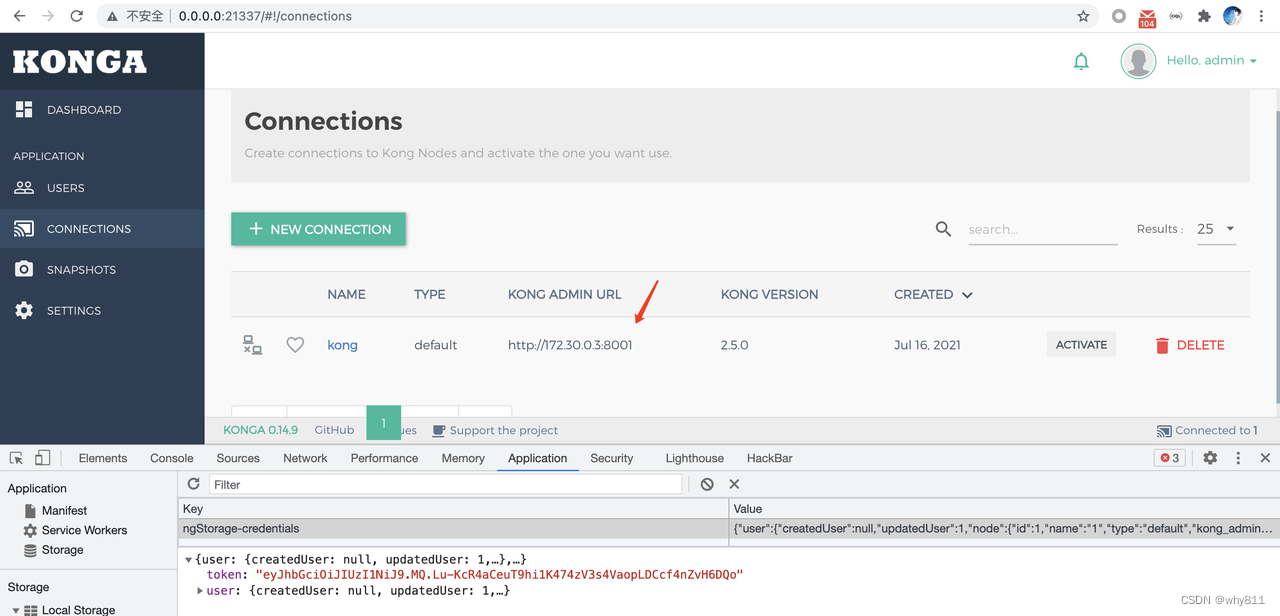
KongA 任意用户登录漏洞分析
KongA 简介 KongA 介绍 KongA 是 Kong 的一个 GUI 工具。GitHub 地址是 https://github.com/pantsel/konga 。 KongA 概述 KongA 带来的一个最大的便利就是可以很好地通过UI观察到现在 Kong 的所有的配置,并且可以对于管理 Kong 节点 漏洞成因 未设置TOKEN_SECRE…...
吉力宝:智能科技鞋品牌步力宝引领传统产业创新思维
在现代经济环境下,市场经济下产品的竞争非常的激烈,如果没有营销,产品很可能不被大众认可,酒香也怕巷子深,许多传统产业不得不面临前所未有的挑战。而为了冲出这个“巷子”,许多企业需要采用创新思维&#…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
