当前位置： 首页 > news >正文

【Leetcode】162.寻找峰值

news 2025/9/13 22:41:20

一、题目

1、题目描述

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5， 其峰值元素为 6。

提示：

  • 1 <= nums.length <= 1000
  • -231 <= nums[i] <= 231 - 1
  • 对于所有有效的 i 都有 nums[i] != nums[i + 1]

2、基础框架

class

相关文章：

【Leetcode】162.寻找峰值

一、题目 1、题目描述 峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。 你可以假设 nums[-1] = nums[n] = -∞ 。 你必须实现时间复杂度为 O(log n…...

编程日记 2023/9/29 19:12:56

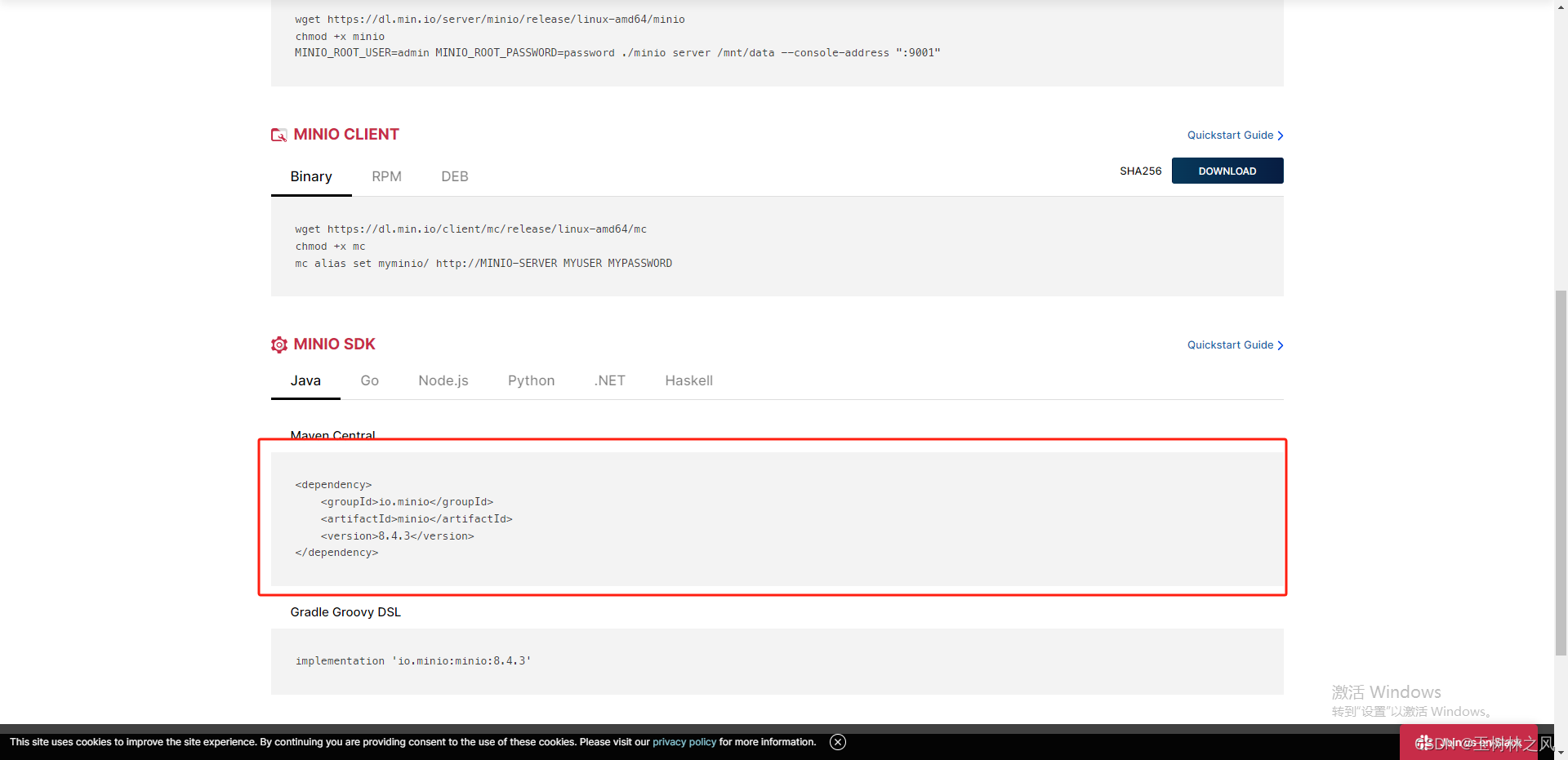
SpringBoot集成MinIO8.0

一、安装MinIO 中文官网地址&#xff1a;https://www.minio.org.cn/download.shtml 官网地址&#xff1a;https://min.io/download 官网有相应的安装命令&#xff0c;可查看 建议引用相应版本的依赖 二、集成SpringBoot 1.引入依赖 <dependency><groupId>io.…...

编程日记 2023/9/29 19:03:47

蓝桥等考Python组别五级007

第一部分：选择题 1、Python L5 （15分） 表达式“not a > 0”等价于下面哪个表达式？（ ） a < 0a == 0a <= 0a in 0正确答案：C 2、Python L5 （15分） 执行下面的程序，当用键盘输入10时，输出结果是（ ）。 n &...

编程日记 2023/9/29 19:02:46

【装机】通过快捷键设置BIOS从U盘启动

当要重装系统的时候,是否会遇到一个问题,进入bios的时候就开始凌乱了,因为不懂得怎么用bios设置u盘启动.不要着急,下面来一波小白装机教程 总的来讲&#xff0c;设置电脑从U盘启动一共有两种方法&#xff1a; 第一种&#xff1a;开机时候按快捷键&#xff0c;然后选择U盘启动第…...

编程日记 2023/9/29 18:59:44

关于操作系统与内核科普

关于操作系统与内核科普 一.什么是操作系统 操作系统是管理计算机硬件与软件资源的计算机程序。它为计算机硬件和软件提供了一种中间层。 操作系统是一种软件&#xff0c;主要目的有三种&#xff1a; 一.管理计算机资源&#xff0c;这些资源包括CPU&#xff0c;内存&#xff0…...

编程日记 2023/9/29 18:57:41

算法练习3——删除有序数组中的重复项

LeetCode 26 删除有序数组中的重复项 给你一个 非严格递增排列 的数组 nums &#xff0c;请你 原地 删除重复出现的元素&#xff0c;使每个元素 只出现一次 &#xff0c;返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums …...

编程日记 2023/9/29 18:55:39

《YOLOv5：从入门到实战》报错解决 专栏答疑

前言&#xff1a;Hello大家好&#xff0c;我是小哥谈。《YOLOv5&#xff1a;从入门到实战》专栏上线后&#xff0c;部分同学在学习过程中提出了一些问题&#xff0c;笔者相信这些问题其他同学也有可能遇到。为了让大家可以更好地学习本专栏内容&#xff0c;笔者特意推出了该篇专…...

编程日记 2023/9/29 18:52:37

[2023.09.25]:Rust编写基于web_sys的编辑器：输入光标再次定位的小结

前些天&#xff0c;写了探索Rust编写基于web_sys的WebAssembly编辑器&#xff1a;挑战输入光标定位的实践&#xff0c;经过后续的开发检验&#xff0c;我发现了一个问题&#xff0c;就是光标消失了。为了继续输入&#xff0c;用户需要再次使用鼠标点击。现在我已经弄清楚了导致…...

编程日记 2023/9/29 18:51:35

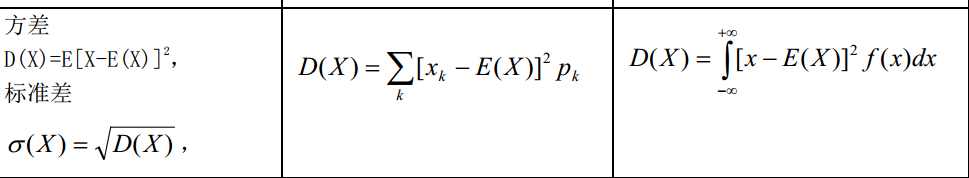
估计、偏差和方差

一、介绍 统计领域为我们提供了很多工具来实现机器学习目标&#xff0c;不仅可以解决训练集上的任务&#xff0c;还可以泛化。基本的概念&#xff0c;例如参数估计、偏差和方差&#xff0c;对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。 二、参数估计 参数估计 是统计学…...

编程日记 2023/9/29 18:50:33

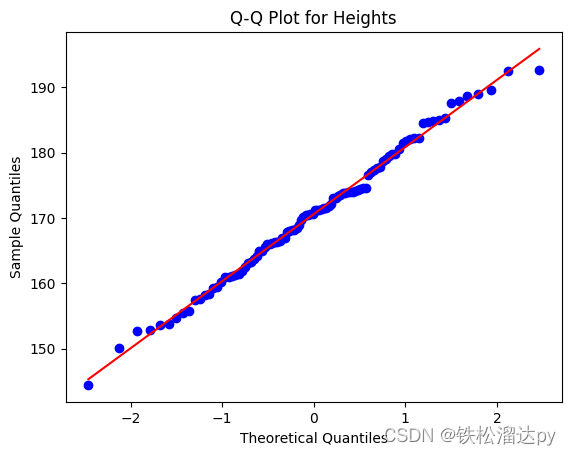
正态分布的概率密度函数|正态分布检验|Q-Q图

正态分布的概率密度函数&#xff08;Probability Density Function&#xff0c;简称PDF&#xff09;的函数取值是指在给定的正态分布参数&#xff08;均值 μ 和标准差 σ&#xff09;下&#xff0c;对于特定的随机变量取值 x&#xff0c;计算得到的概率密度值 f(x)。这个值表示…...

编程日记 2023/9/29 18:47:31

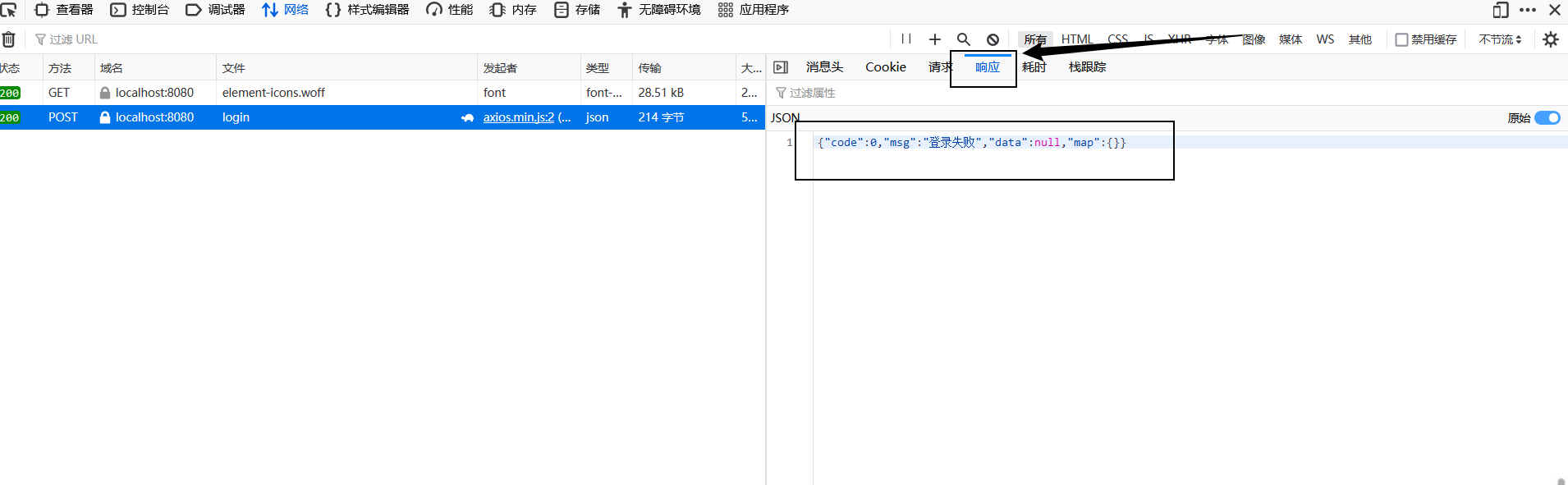
【接口测试】HTTP协议

一、HTTP 协议基础 HTTP 简介 HTTP 是一个客户端终端&#xff08;用户&#xff09;和服务器端&#xff08;网站&#xff09;请求和应答的标准&#xff08;TCP&#xff09;。通常是由客户端发起一个请求&#xff0c;创建一个到服务器的 TCP 连接&#xff0c;当服务器监听到客户…...

编程日记 2023/9/29 18:46:30

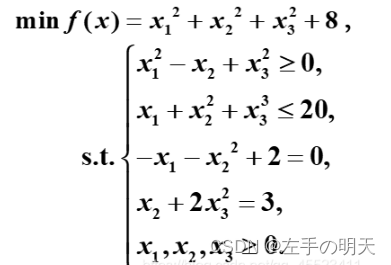
【重新定义matlab强大系列十四】基于问题求解有/无约束非线性优化

&#x1f517; 运行环境&#xff1a;Matlab &#x1f6a9; 撰写作者&#xff1a;左手の明天 &#x1f947; 精选专栏&#xff1a;《python》 &#x1f525; 推荐专栏&#xff1a;《算法研究》 #### 防伪水印——左手の明天 #### &#x1f497; 大家好&#x1f917;&#x1f91…...

编程日记 2023/9/29 18:45:28

MySQL 索引介绍和最佳实践

目录 一、前言二、索引类型1.1 主键索引&#xff08;PRIMARY KEY&#xff09;1.2 唯一索引&#xff08;UNIQUE&#xff09;1.3 普通索引&#xff08;NORMAL&#xff09;1.3.1 单列普通索引1.3.2 单列前缀普通索引1.3.3 多列普通索引1.3.4 多列前缀普通索引 1.4 空间索引&#x…...

编程日记 2023/9/29 18:42:25

区块链（7）：p2p去中心化之初始化websoket服务端

1 整个流程梳理 服务开启onStart()连接打开onOpen()处理接收到的消息onMesage()连接关闭onClose()异常处理onError()2 创建p2p实现类 package com.example.demo.service;import com.example.demo.entity.BlockChain; import org.java_websocket.WebSocket; import org.java_we…...

编程日记 2023/9/29 18:40:23

原型、原型链、判断数据类型

目录 作用 原型链 引用类型&#xff1a;__proto__(隐式原型)属性&#xff0c;属性值是对象函数&#xff1a;prototype(原型)属性&#xff0c;属性值是对象 Function&#xff1a;本身也是函数 相关方法 person.prototype.isPrototypeOf(stu) Object.getPrototypeOf(objec…...

编程日记 2023/9/29 18:39:22

pycharm中配置torch

在控制台cmd中安装好torch后&#xff0c;在pycharm中使用torch&#xff0c;需要进行简单设置即可。 在pycharm中新建一个工程&#xff0c;在file文件中打开setting 在setting中找到project interpreter编译器 找到conda environment的环境配置&#xff0c;设置好相应的目录 新…...

编程日记 2023/9/29 18:38:21

什么是Times New Roman 字体

如何评价 Times New Roman 字体&#xff1f;&#xff1a;https://www.zhihu.com/question/24614549?sortcreated 新罗马字体是Times New Roman字体&#xff0c;是Office Word默认自带的英文字体之一。 中英文字体 写作中&#xff0c;英文和数字的标准字体为 Times New Roma…...

编程日记 2023/9/29 18:37:20

企业会议新闻稿怎么写?会议类新闻稿如何撰写?

企业会议新闻稿是企业对外传递信息的重要途径之一&#xff0c;它能够将企业的决策、动态以及成果展示给公众。本文伯乐网络传媒将详细解析企业会议新闻稿的写作要点和技巧&#xff0c;以及常见问题及解决方法&#xff0c;帮助大家更好地完成企业会议新闻稿的撰写工作。 一、企业…...

编程日记 2023/9/29 18:36:19

算法 滑动窗口最大值-(双指针+队列)

牛客网: BM45 题目: 数组num, 窗口大小size, 所有窗口内的最大值 思路: 用队列作为窗口&#xff0c;窗口内存储数组坐标&#xff0c;left window[0], right从数组0开始遍历完数组&#xff0c;每次新增元素时&#xff0c;(1)先对窗口大小进行收缩到size大小范围&#xff0c;即…...

编程日记 2023/9/29 18:35:17

Java 并发编程面试题——BlockingQueue

目录 1.什么是阻塞队列 (BlockingQueue)&#xff1f;2.BlockingQueue 有哪些核心方法&#xff1f;3.BlockingQueue 有哪些常用的实现类&#xff1f;3.1.ArrayBlockingQueue3.2.DelayQueue3.3.LinkedBlockingQueue3.4.PriorityBlockingQueue3.5.SynchronousQueue 4.✨BlockingQu…...

编程日记 2023/9/29 18:34:16

Oracle查询表空间大小

1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

编程新知 2025/9/13 3:49:22

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/9/13 8:59:33

【JavaWeb】Docker项目部署

引言 之前学习了Linux操作系统的常见命令&#xff0c;在Linux上安装软件&#xff0c;以及如何在Linux上部署一个单体项目&#xff0c;大多数同学都会有相同的感受&#xff0c;那就是麻烦。 核心体现在三点&#xff1a; 命令太多了&#xff0c;记不住 软件安装包名字复杂&…...

编程新知 2025/9/12 23:22:13

return this；返回的是谁

一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请&#xff0c;不同级别的经理有不同的审批权限&#xff1a; // 抽象处理者&#xff1a;审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

编程新知 2025/7/6 12:42:16

CRMEB 中 PHP 短信扩展开发：涵盖一号通、阿里云、腾讯云、创蓝

目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为&#xff1a;一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

编程新知 2025/9/12 22:08:06

C++ 设计模式 《小明的奶茶加料风波》

&#x1f468;‍&#x1f393; 模式名称&#xff1a;装饰器模式&#xff08;Decorator Pattern&#xff09; &#x1f466; 小明最近上线了校园奶茶配送功能&#xff0c;业务火爆&#xff0c;大家都在加料&#xff1a; 有的同学要加波霸 &#x1f7e4;&#xff0c;有的要加椰果…...

编程新知 2025/9/1 17:56:35

Elastic 获得 AWS 教育 ISV 合作伙伴资质，进一步增强教育解决方案产品组合

作者&#xff1a;来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布&#xff0c;Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明&#xff0c;Elastic 作为 …...

编程新知 2025/9/3 21:29:46

41道Django高频题整理(附答案背诵版)

解释一下 Django 和 Tornado 的关系&#xff1f; Django和Tornado都是Python的web框架&#xff0c;但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架&#xff0c;鼓励快速开发和干净、实用的设计。它遵循MVC设计&#xff0c;并强调代码复用。Django有…...

编程新知 2025/7/15 10:00:19

vxe-table vue 表格复选框多选数据，实现快捷键 Shift 批量选择功能

vxe-table vue 表格复选框多选数据&#xff0c;实现快捷键 Shift 批量选择功能 查看官网&#xff1a;https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...

编程新知 2025/9/9 10:00:20

结构性-代理模式

动态代理主要是为了处理重复创建模板代码的场景。 使用示例 public interface MyInterface {String doSomething(); }public class MyInterfaceImpl implements MyInterface{Overridepublic String doSomething() {return "接口方法dosomething";} }public class M…...

编程新知 2025/9/10 13:26:05