当前位置： 首页 > news >正文

什么是DevOps

news 2026/2/7 21:05:23

文章目录

  • 一、概念
  • 二、地位
  • 三、目标
  • 四、要求
  • 五、具体手段

一、概念

是一组过程、方法与系统的统称，有助于打破开发、测试、运维、交付部门之间的壁垒，提高部门间的沟通协助能力。

二、地位

应成为公司的一种理念、文化、哲学。

三、目标

实现更加高效的部署、测试、交付，持续提高产品的迭代效率和可靠性，让开发写的代码"所写即所见（能够快速部署进行展现），所见即所得（建立完善的反馈机制，第一时间知道代码的质量）"

四、要求

1、在产品设计时，不仅要从开发角度考虑，还需从测试、运维、交付角度去综合考虑

2、最大程度减少人工干预，不断提高其自动化、智能化

3、支持多次提交代码，快速编译、部署、测试

五、具体手段

1、使用Git进行代码管理

2、使用持续集成工具(如Jenkins）进行编译打包，使用Docker构建镜像

3、用Jfrog管理制品，Harbor存放Docker镜像

5、使用K8S编排、管理容器

6、使用测试工具（如sonarQube、Selenium)进行质量把控、集成测试

7、使用持续部署工具（如Argo CD）进行版本更新

8、使用自动化运维工具(如Ansible）进行维护管理、客户交付

9、使用监控系统（如Prometheus）进行24小时不间断监控，并实现自动告警、通知、修复

10、搭建完备的日志系统（如ELK），让问题可追溯

相关文章：

什么是DevOps

文章目录 一、概念二、地位三、目标四、要求五、具体手段 一、概念 是一组过程、方法与系统的统称，有助于打破开发、测试、运维、交付部门之间的壁垒，提高部门间的沟通协助能力。 二、地位 应成为公司的一种理念、文化、哲学。 三、目标 实现更加高…...

编程日记 2023/9/29 19:29:12

力扣每日一题

605. 种花问题 - 力扣&#xff08;LeetCode&#xff09; 动态规划 class Solution { public:bool canPlaceFlowers(vector<int>& flowerbed, int n) {int m flowerbed.size();if(1 m)return !flowerbed[0] > n;else if(2 m)return ((!flowerbed[0] &&…...

编程日记 2023/9/29 19:27:08

测试OpenCvSharp库的模板匹配功能

微信公众号“Dotnet讲堂”的文章《c#实现模板匹配&#xff0c;并输出匹配坐标》&#xff08;参考文献1&#xff09;中介绍了采用OpenCVSharp库实现模板匹配功能&#xff0c;也即在目标图片中定位指定图片内容的示例&#xff0c;本文参照参考文献1-4&#xff0c;学习并测试OpenC…...

编程日记 2023/9/29 19:26:07

网络编程day04（网络属性函数、广播、组播、TCP并发）

今日任务 对于newfd的话&#xff0c;最好是另存然后传入给分支线程&#xff0c;避免父子线程操作同一个文件描述符 ------------在tcp多线程服务端---------- 如果使用全局变量&#xff0c;或者指针方式间接访问&#xff0c;会导致所有线程共用一份newfd和cin&#xff0c;那么…...

编程日记 2023/9/29 19:22:04

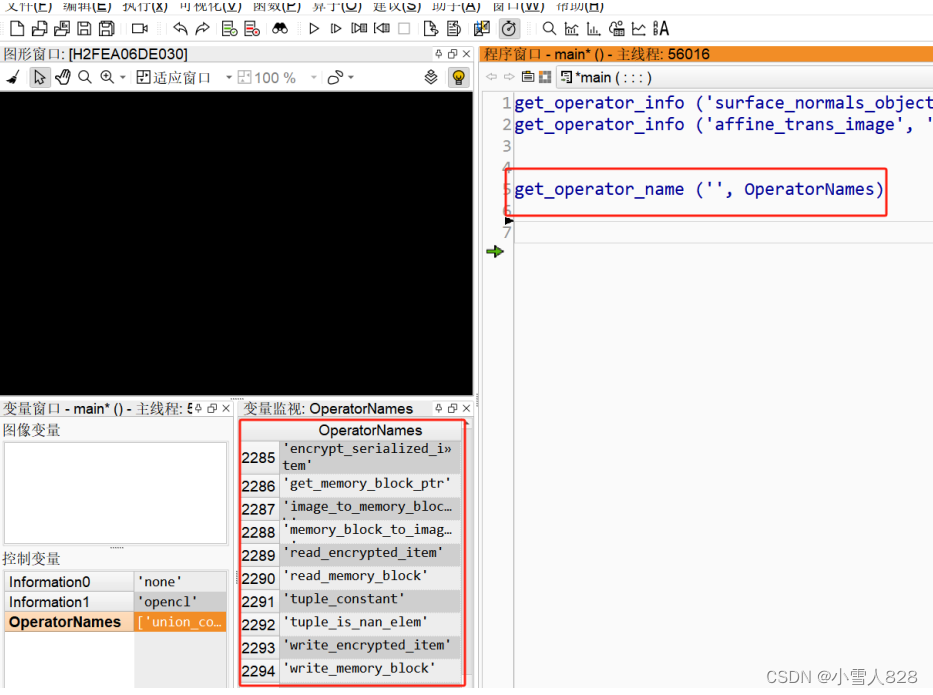
HALCON支持GPU加速的算子有哪些？

参考例程get_operator_info。 get_opencl_operators这里可以查看到所有支持gpu加速的算子。 支持的算子列表&#xff1a; crop_rectangle1&#xff0c;deviation_image&#xff0c;mean_image&#xff0c;points_harris&#xff0c;gray_opening_shape&#xff0c; gray_dilat…...

编程日记 2023/9/29 19:20:02

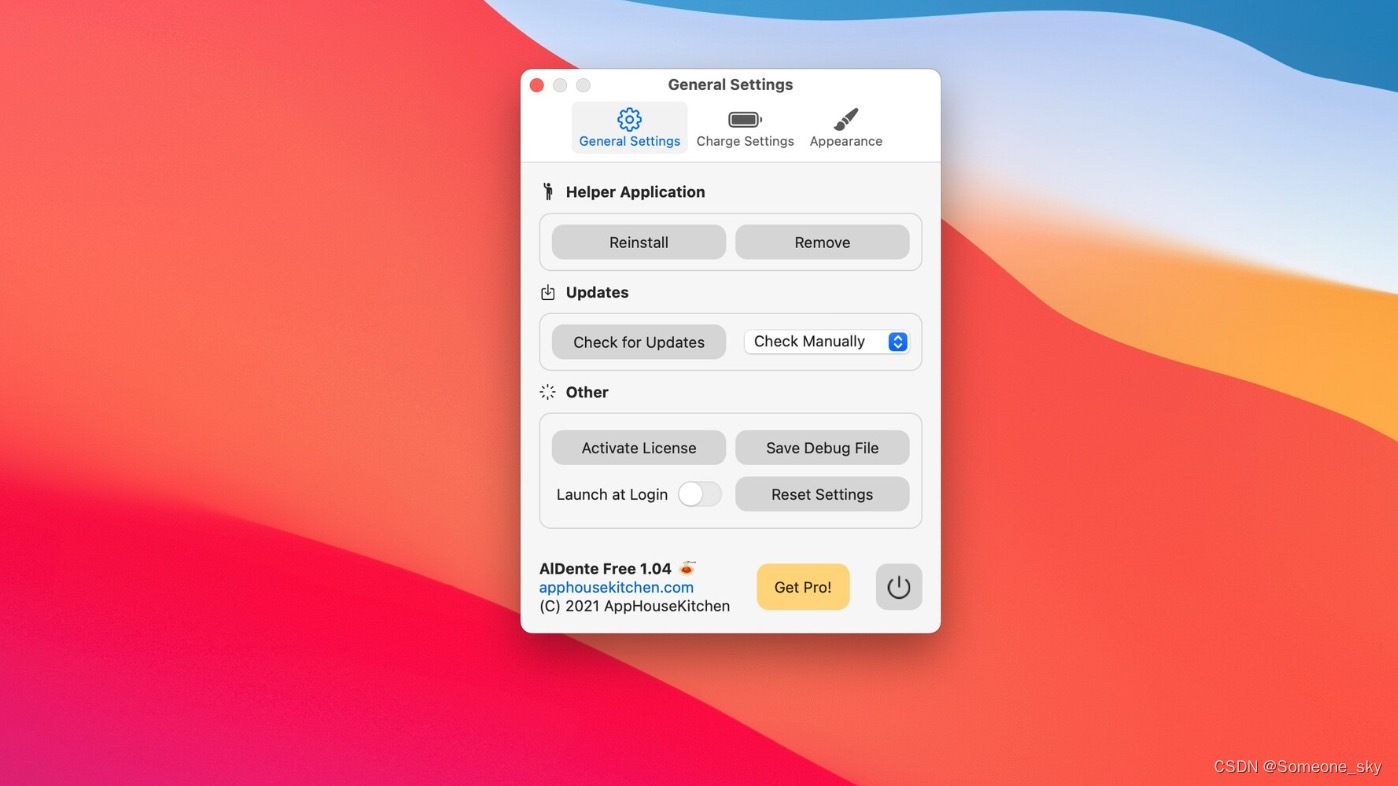
MacBook Pro 电池电量限制充电怎么设置AlDente Pro for Mac最大充电限制工具

通过充电电量限制工具可以更好的保护MacBook Pro的电池&#xff0c;通过 AlDente Pro 您可以设置电池的最大充电百分比设置为 20&#xff05; 至 100&#xff05;&#xff0c;然后&#xff0c;它将保持在所需的电池百分比&#xff0c;然后再次使用电源适配器进行充电。 AlDent…...

编程日记 2023/9/29 19:17:00

毕业设计选题之Java+springboot线上蔬菜销售与配送系统（源码+调试+开题+lw）

&#x1f495;&#x1f495;作者&#xff1a;计算机源码社 &#x1f495;&#x1f495;个人简介&#xff1a;本人七年开发经验&#xff0c;擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等&#xff0c;大家有这一块的问题可以一起交流&#xff01; &#x1f495;&…...

编程日记 2023/9/29 19:15:59

【Leetcode】162.寻找峰值

一、题目 1、题目描述 峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。 你可以假设 nums[-1] = nums[n] = -∞ 。 你必须实现时间复杂度为 O(log n…...

编程日记 2023/9/29 19:12:56

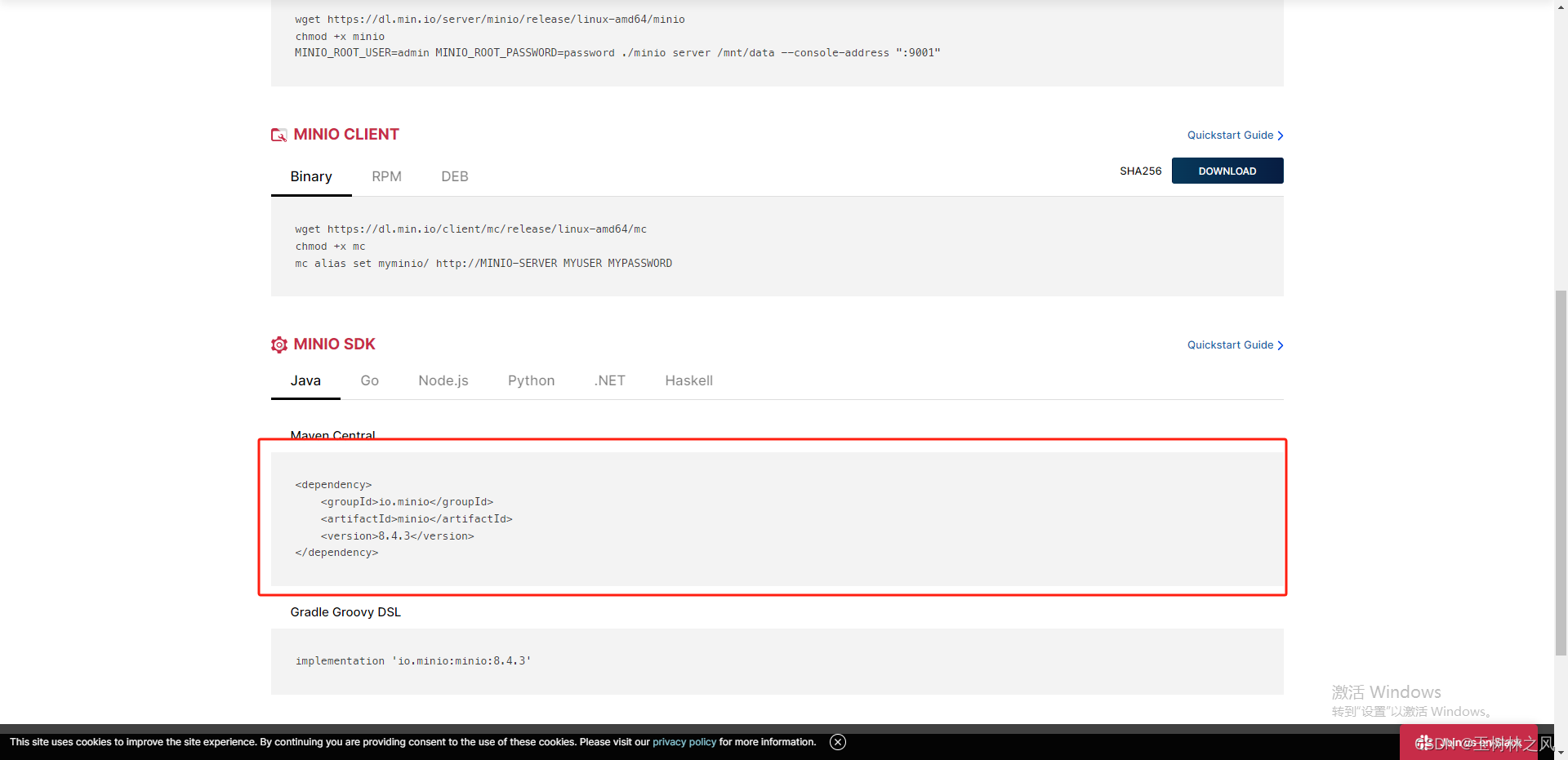
SpringBoot集成MinIO8.0

一、安装MinIO 中文官网地址&#xff1a;https://www.minio.org.cn/download.shtml 官网地址&#xff1a;https://min.io/download 官网有相应的安装命令&#xff0c;可查看 建议引用相应版本的依赖 二、集成SpringBoot 1.引入依赖 <dependency><groupId>io.…...

编程日记 2023/9/29 19:03:47

蓝桥等考Python组别五级007

第一部分：选择题 1、Python L5 （15分） 表达式“not a > 0”等价于下面哪个表达式？（ ） a < 0a == 0a <= 0a in 0正确答案：C 2、Python L5 （15分） 执行下面的程序，当用键盘输入10时，输出结果是（ ）。 n &...

编程日记 2023/9/29 19:02:46

【装机】通过快捷键设置BIOS从U盘启动

当要重装系统的时候,是否会遇到一个问题,进入bios的时候就开始凌乱了,因为不懂得怎么用bios设置u盘启动.不要着急,下面来一波小白装机教程 总的来讲&#xff0c;设置电脑从U盘启动一共有两种方法&#xff1a; 第一种&#xff1a;开机时候按快捷键&#xff0c;然后选择U盘启动第…...

编程日记 2023/9/29 18:59:44

关于操作系统与内核科普

关于操作系统与内核科普 一.什么是操作系统 操作系统是管理计算机硬件与软件资源的计算机程序。它为计算机硬件和软件提供了一种中间层。 操作系统是一种软件&#xff0c;主要目的有三种&#xff1a; 一.管理计算机资源&#xff0c;这些资源包括CPU&#xff0c;内存&#xff0…...

编程日记 2023/9/29 18:57:41

算法练习3——删除有序数组中的重复项

LeetCode 26 删除有序数组中的重复项 给你一个 非严格递增排列 的数组 nums &#xff0c;请你 原地 删除重复出现的元素&#xff0c;使每个元素 只出现一次 &#xff0c;返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums …...

编程日记 2023/9/29 18:55:39

《YOLOv5：从入门到实战》报错解决 专栏答疑

前言&#xff1a;Hello大家好&#xff0c;我是小哥谈。《YOLOv5&#xff1a;从入门到实战》专栏上线后&#xff0c;部分同学在学习过程中提出了一些问题&#xff0c;笔者相信这些问题其他同学也有可能遇到。为了让大家可以更好地学习本专栏内容&#xff0c;笔者特意推出了该篇专…...

编程日记 2023/9/29 18:52:37

[2023.09.25]:Rust编写基于web_sys的编辑器：输入光标再次定位的小结

前些天&#xff0c;写了探索Rust编写基于web_sys的WebAssembly编辑器&#xff1a;挑战输入光标定位的实践&#xff0c;经过后续的开发检验&#xff0c;我发现了一个问题&#xff0c;就是光标消失了。为了继续输入&#xff0c;用户需要再次使用鼠标点击。现在我已经弄清楚了导致…...

编程日记 2023/9/29 18:51:35

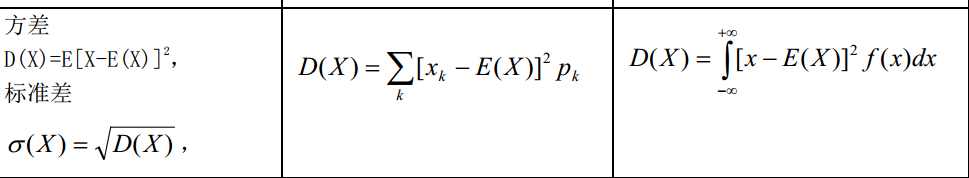
估计、偏差和方差

一、介绍 统计领域为我们提供了很多工具来实现机器学习目标&#xff0c;不仅可以解决训练集上的任务&#xff0c;还可以泛化。基本的概念&#xff0c;例如参数估计、偏差和方差&#xff0c;对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。 二、参数估计 参数估计 是统计学…...

编程日记 2023/9/29 18:50:33

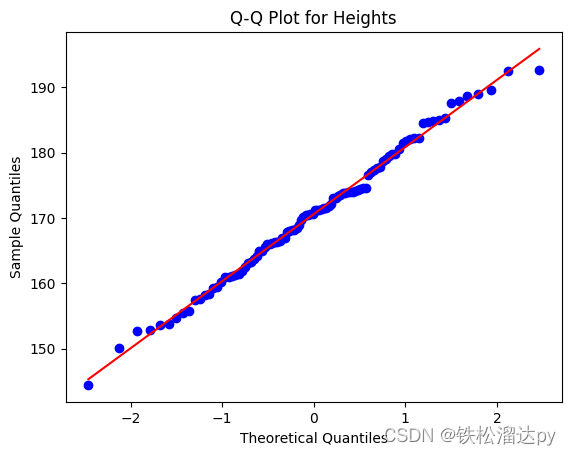
正态分布的概率密度函数|正态分布检验|Q-Q图

正态分布的概率密度函数&#xff08;Probability Density Function&#xff0c;简称PDF&#xff09;的函数取值是指在给定的正态分布参数&#xff08;均值 μ 和标准差 σ&#xff09;下&#xff0c;对于特定的随机变量取值 x&#xff0c;计算得到的概率密度值 f(x)。这个值表示…...

编程日记 2023/9/29 18:47:31

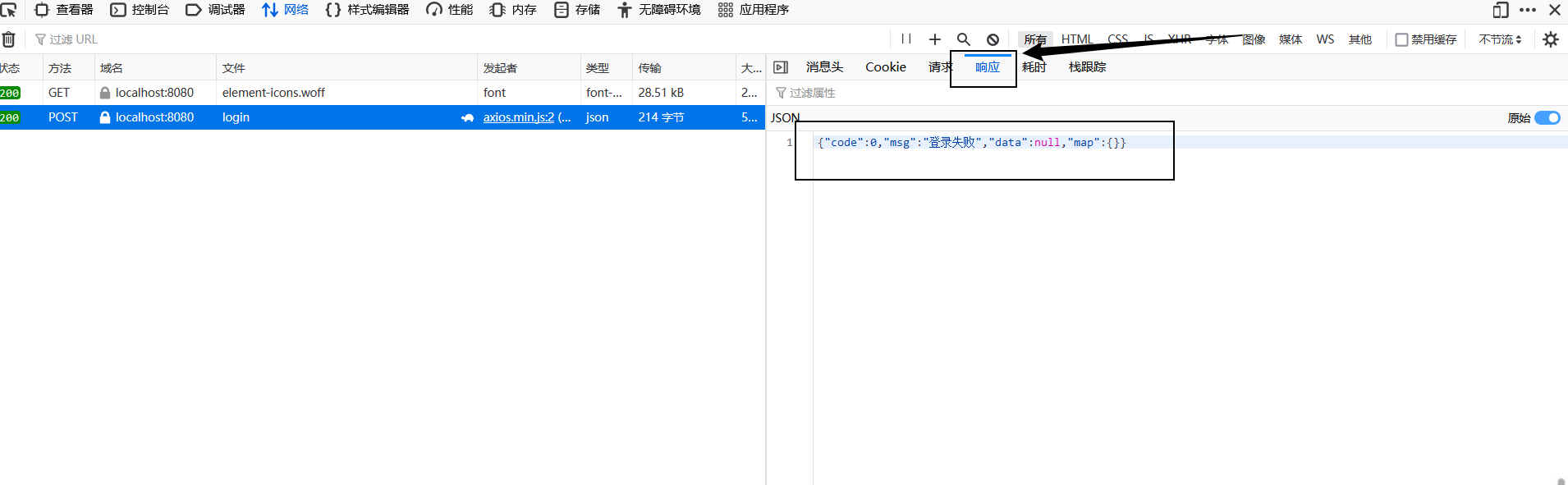
【接口测试】HTTP协议

一、HTTP 协议基础 HTTP 简介 HTTP 是一个客户端终端&#xff08;用户&#xff09;和服务器端&#xff08;网站&#xff09;请求和应答的标准&#xff08;TCP&#xff09;。通常是由客户端发起一个请求&#xff0c;创建一个到服务器的 TCP 连接&#xff0c;当服务器监听到客户…...

编程日记 2023/9/29 18:46:30

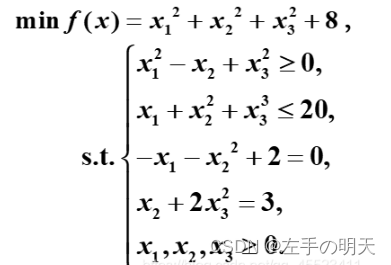
【重新定义matlab强大系列十四】基于问题求解有/无约束非线性优化

&#x1f517; 运行环境&#xff1a;Matlab &#x1f6a9; 撰写作者&#xff1a;左手の明天 &#x1f947; 精选专栏&#xff1a;《python》 &#x1f525; 推荐专栏&#xff1a;《算法研究》 #### 防伪水印——左手の明天 #### &#x1f497; 大家好&#x1f917;&#x1f91…...

编程日记 2023/9/29 18:45:28

MySQL 索引介绍和最佳实践

目录 一、前言二、索引类型1.1 主键索引&#xff08;PRIMARY KEY&#xff09;1.2 唯一索引&#xff08;UNIQUE&#xff09;1.3 普通索引&#xff08;NORMAL&#xff09;1.3.1 单列普通索引1.3.2 单列前缀普通索引1.3.3 多列普通索引1.3.4 多列前缀普通索引 1.4 空间索引&#x…...

编程日记 2023/9/29 18:42:25

【Oracle APEX开发小技巧12】

有如下需求&#xff1a; 有一个问题反馈页面&#xff0c;要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据&#xff0c;方便管理员及时处理反馈。 我的方法&#xff1a;直接将逻辑写在SQL中&#xff0c;这样可以直接在页面展示 完整代码&#xff1a; SELECTSF.FE…...

编程新知 2026/2/7 17:35:15

【力扣数据库知识手册笔记】索引

索引 索引的优缺点 优点1. 通过创建唯一性索引&#xff0c;可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度&#xff08;创建索引的主要原因&#xff09;。3. 可以加速表和表之间的连接&#xff0c;实现数据的参考完整性。4. 可以在查询过程中&#xff0c;…...

编程新知 2026/1/25 4:36:37

CMake基础：构建流程详解

目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

编程新知 2026/2/2 7:39:34

c++ 面试题(1)-----深度优先搜索（DFS）实现

操作系统&#xff1a;ubuntu22.04 IDE:Visual Studio Code 编程语言&#xff1a;C11 题目描述 地上有一个 m 行 n 列的方格&#xff0c;从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子&#xff0c;但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

编程新知 2026/1/10 10:16:16

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/29 18:30:30

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言 在数据驱动的背景下&#xff0c;知识图谱凭借其高效的信息组织能力&#xff0c;正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合&#xff0c;探讨知识图谱开发的实现细节&#xff0c;帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/17 21:39:04

什么是Ansible Jinja2

理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具&#xff0c;可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板&#xff0c;允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板&#xff0c;并通…...

编程新知 2026/2/6 1:00:25

大语言模型（LLM）中的KV缓存压缩与动态稀疏注意力机制设计

随着大语言模型&#xff08;LLM&#xff09;参数规模的增长&#xff0c;推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长&#xff0c;而KV缓存的内存消耗可能高达数十GB&#xff08;例如Llama2-7B处理100K token时需50GB内存&a…...

编程新知 2026/1/28 1:40:03

中医有效性探讨

文章目录 西医是如何发展到以生物化学为药理基础的现代医学&#xff1f;传统医学奠基期&#xff08;远古 - 17 世纪&#xff09;近代医学转型期&#xff08;17 世纪 - 19 世纪末&#xff09;​现代医学成熟期&#xff08;20世纪至今&#xff09; 中医的源远流长和一脉相承远古至…...

编程新知 2026/1/23 7:56:54

Spring是如何解决Bean的循环依赖：三级缓存机制

1、什么是 Bean 的循环依赖 在 Spring框架中，Bean 的循环依赖是指多个 Bean 之间‌互相持有对方引用‌，形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路，例如： 双向依赖：Bean A 依赖 Bean B，同时 Bean B 也依赖 Bean A（A↔B）。链条循环： Bean A → Bean…...

编程新知 2025/7/25 1:21:53