LeetCode 1049. 最后一块石头的重量 II
1049. 最后一块石头的重量 II - 力扣(LeetCode)
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40] 输出:5

【思路】尽量把这些石头分成重量总和近似相等的两堆。分成数值近似相等的两个集合,也就是这里边的两堆石头。尽量凑成,凑不成也没关系。凑不成的话那两堆石头相撞的话,所剩的重量它也一定是最小的。那此时这就是一个背包问题,每一个物品只能用一次,所以说这就是一个0-1背包。
本题和 LeetCode 416.分割等和子集几乎就是一样的, 唯一的区别就是在最后判断的时候,是有一点出入的。
- 在0-1背包中的dp[j]
dp[j] 背包容量j 最大价值dp[j]
最大重量dp[j]
dp[j] = max(dp[j],dp[j-weight[i]] + value[j]);
由于在本题中,价值和重量相等,
dp[j] = max(dp[j],dp[j-stones[i]] + stones[i]);
- 可以求出一堆石头的重量,也就是 dp[target];
- 也就可以求出另一堆石头的重量,也就是 sum - dp[target]
- 然后这两堆石头进行碰撞:(sum - dp[target]) - dp[target]
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int i=0;i<stones.size();i++) {sum += stones[i];}int target = sum / 2;vector<int> dp(target+1,0);for(int i=0;i<stones.size();i++) { // 遍历物品for(int j=target;j>=stones[i];j--) { // 遍历背包dp[j] = max(dp[j],dp[j-stones[i]] + stones[i]);}}return sum - dp[target] -dp[target];}
};// stones = [2,7,4,1,8,1]
// 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y// 2 7 4 1 8 1// 思路:尽量分成重量差不多的两堆,然后再进行相减
// 思考:那如何分成这样的两堆呢?// 1.dp[j]
// dp[j]中的j表示容量,那么最大容量(重量)是多少呢,就是所有石头的重量和// 2.确定target
// 2 + 7 + 4 + 1 + 8 + 1 = 23
// target = sum / 2 = 23/2 = 11;
// {2,7,1,1} {4,8}
// 11 - 10 = 1// ① dp[target];
// ② sum - dp[target]
// ③ (sum - dp[target]) - dp[target] // 3.动态递归方程
// dp[j] = max(dp[j],dp[j-stones[i]] + stones[i]);// 4.初始化dp
// dp[0] = 0
// 一维数组dp初始化为0
// vector<int> dp(target+1,0);// 5.遍历
// 先遍历物品,再从后往前遍历背包// 价值 重量
// 物品0 2 2
// 物品1 7 7
// 物品2 4 4
// 物品3 1 1
// 物品4 8 8
// 物品5 1 1// 0 1 2 3 4 5 6 7 8 9 10 11 背包重量j
// | | | | | | | | | | | |
// 0 0 0 0 0 0 0 0 0 0 0 0 初始化dp
// 0 0 2 2 2 2 2 2 2 2 2 2 (可挑选物品0)->产生最大价值
// 0 0 2 2 2 2 2 7 7 9 9 9 (可挑选物品0、物品1)->产生最大价值
// 0 0 2 2 4 4 6 7 7 9 9 11 (可挑选物品0、物品1、物品2)->产生最大价值
// 0 1 2 3 4 5 6 7 8 9 10 11 (可挑选物品0、物品1、物品2、物品3)->产生最大价值
// 0 1 2 3 4 5 6 7 8 9 10 11 (可挑选物品0、物品1、物品2、物品3、物品4)->产生最大价值
// 0 1 2 3 4 5 6 7 8 9 10 11 (可挑选物品0、物品1、物品2、物品3、物品4、物品5)->产生最大价值来自代码随想录的课堂截图

>>往期文章:
解决0-1背包问题(方案一):二维dp数组_呵呵哒( ̄▽ ̄)"的博客-CSDN博客
解决0-1背包问题(方案二):一维dp数组(滚动数组)_呵呵哒( ̄▽ ̄)"的博客-CSDN博客
相关文章:

LeetCode 1049. 最后一块石头的重量 II
1049. 最后一块石头的重量 II - 力扣(LeetCode) 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y&am…...

Golang中的类型转换介绍
Golang中存在4种类型转换,分别是:断言、显式、隐式、强制。下面我将一一介绍每种转换使用场景和方法 一、断言类型转换 主要是判断变量是否可以转换成某一类型。断言主要用于变量是interface{}类型(接口类型)的情况,…...

本人碰到的RN项目的坑
1.路径问题 路径不能含有中文 2.下载jar\aar包超时问题 手动下载:任意位置新建个文件夹,然后点击超时的jar包链接跳转到浏览器后下载到这个文件夹内,返回报错的地方找到报错的包名(com或者org开头的),然后去这个路径下找到对应的包名 C:\Users\22560\.gradle\caches\module…...

EcmaScript标准-导入与导出-js
ECMAScript是一种由Ecma国际(前身为欧洲计算机制造商协会,European Computer Manufacturers Association)通过ECMA-262标准化的脚本程序设计语言。这种语言在万维网上应用广泛,它往往被称为JavaScript或JScript,所以它…...

如何将matlab中的mat矩阵文件在python中读取出来
先安装hdf5storage这个包 pip3 install hdf5storage 然后在当前目录下放入要读取的mat文件 # 将matlab中的mat文件读取出来 import hdf5storagedata hdf5storage.loadmat(inputWeights.mat) print(data[inputWeights])...
)
解释C语言中 6.18f (浮点数常量后缀)
在C语言中,例如6.18f ,这是一个浮点数常量。 6.18 是一个浮点数,而后缀 f 表示该浮点数是单精度浮点数。 在C语言中,默认的浮点数常量类型是双精度浮点数,如果希望使用单精度浮点数,可以在常量后面加上 f…...

Pandas 2.1中的新改进和新功能
大家好,Pandas 2.1于2023年8月30日发布,跟随本文一起看看这个版本引入了哪些新内容,以及它如何帮助用户改进Pandas的工作负载,包含了一系列改进和一组新的弃用功能。 Pandas 2.1在Pandas 2.0中引入的PyArrow集成基础上进行了大量…...
关键字)
c#static(静态)关键字
在C#中,static关键字有多种用途,可以用于声明静态成员、静态类和静态方法。 静态成员:使用static关键字声明的成员属于类,而不是类的实例。静态成员在类第一次被使用之前就被初始化,且只有一个副本存在于内存中&#x…...
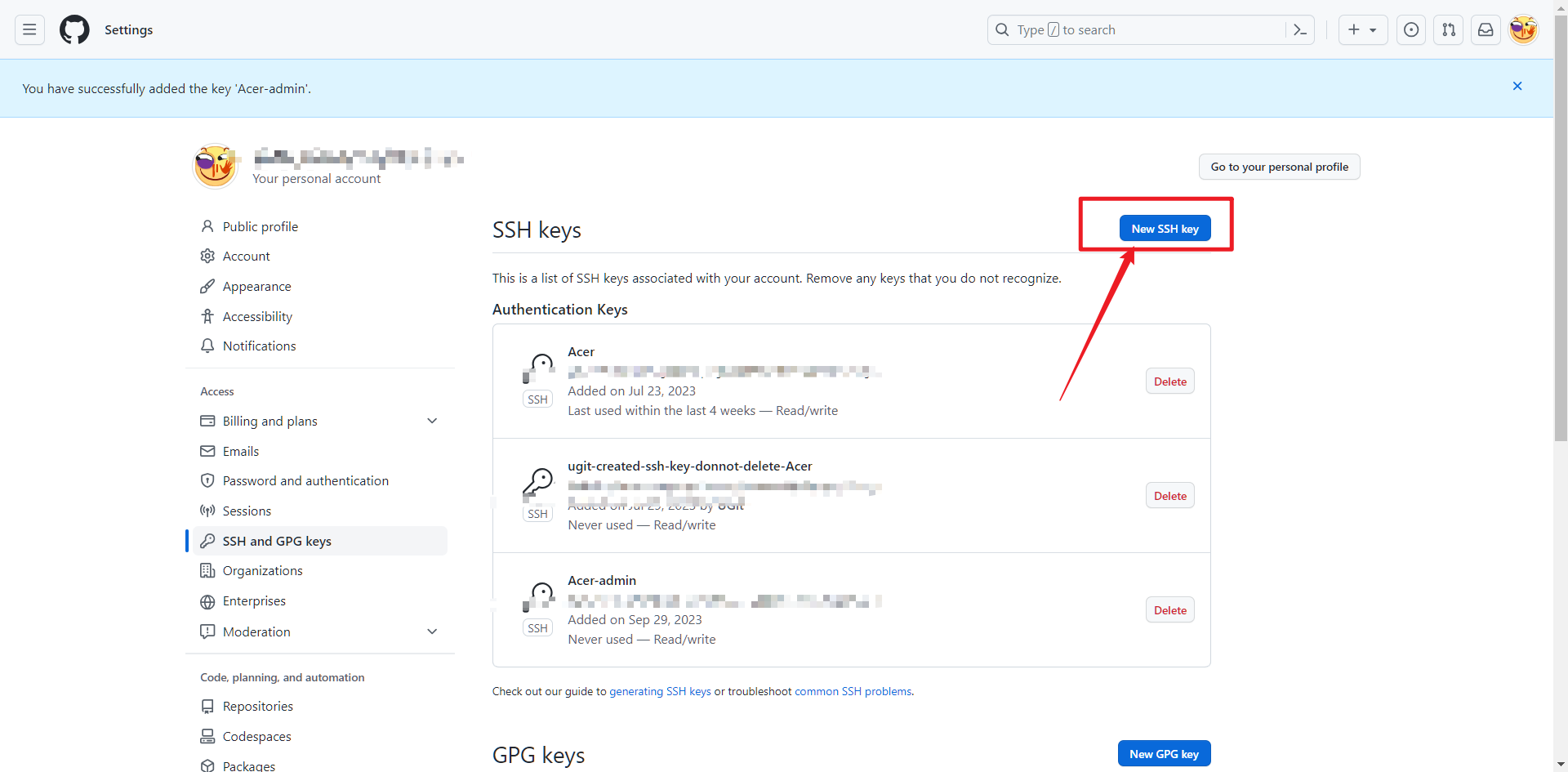
GitHub配置SSH key
GitHub配置SSH key Git配置信息并生成密钥 设置用户名和密码 设置用户名 git config --global user.name "用户名" 设置邮箱 git confir --global user.email "邮箱" 生成密钥 ssh-keygen -t rsa -C "邮箱" 查看密钥 到密钥所保存的位置 复…...

文件审计及文件完整性监控
什么是文件审核 对文件服务器中发生的所有事件的检查称为文件审核。这包括监视文件访问,其中包含谁访问了什么文件、何时以及从何处访问的详细信息;对访问最多和修改的文件的分析;成功和失败的文件访问尝试;等等。文件服务器审核过程的主要目标是跟踪在配置的服务器…...

华为智能企业远程办公安全解决方案(1)
华为智能企业远程办公安全解决方案(1) 课程地址方案背景需求分析企业远程办公业务概述企业远程办公安全风险分析企业远程办公环境搭建需求分析 方案设计组网架构设备选型方案亮点 课程地址 本方案相关课程资源已在华为O3社区发布,可按照以下…...

k8s中常用命令总结
文章目录 进入pod容器的命令pod中只有1个用户容器pod中只有2个(含)以上用户容器 yaml中的字段不清楚后面跟什么,通过explain来查看查看pod内指定容器的日志Pod内各个容器的服务端口不能相同资源对象的创建方式一方式二 查看pod的详细信息查看…...

Logistic map混沌掩盖信号
开学接触了一些有关混沌知识的学习,阅读量一些混沌通信的论文,对于混沌掩盖信号以确保加密通信有一定的兴趣。混沌的产生我选用的是logistic map映射产生混沌,主要就是一个递推公式: 对于这样一个式子,可以看出&#x…...
外包干了2个月,技术有明显退步...
先说一下自己的情况,本科生,18年通过校招进入广州某软件公司,干了接近3年的功能测试,今年国庆,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!可我已经在一个企业干了3年的功能测试&…...
顺序表和链表
顺序表和链表 一.线性表二.顺序表三.链表链表的分类单链表的实现双链表的实现 四.顺序表和链表的区别和联系 一.线性表 常见的线性表:顺序表、链表、栈、队列、字符串 线性表在逻辑上是线性结构,也就说是连续的一条直线,但是在物理结构上并不…...

k8s--架构基础--云控制器管理器
具体来说,云控制器管理器允许用户将集群与云服务提供商的 API 进行连接,以获取与云平台相关的信息和资源。通过这种连接,Kubernetes 可以利用云服务提供商的功能和特性,例如虚拟机、负载均衡器、对象存储等。与此同时,…...
OpenAI 更新 ChatGPT:支持图片和语音输入【附点评】
一、消息正文 9月25日消息,近日OpenAI宣布其对话AI系统ChatGPT进行升级,添加了语音输入和图像处理两个新功能。据OpenAI透露,这些新功能将在未来两周内面向ChatGPT Plus付费用户推出,免费用户也将很快可以使用这些新功能。这标志着ChatGPT继续朝着多模态交互的方向发展,为用户提…...
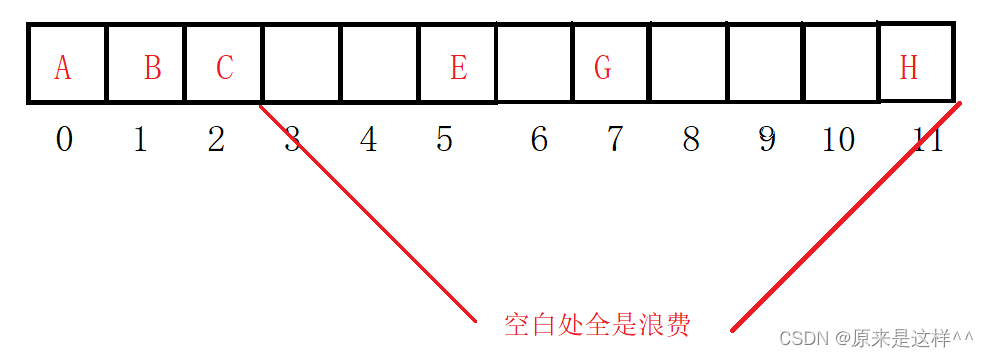
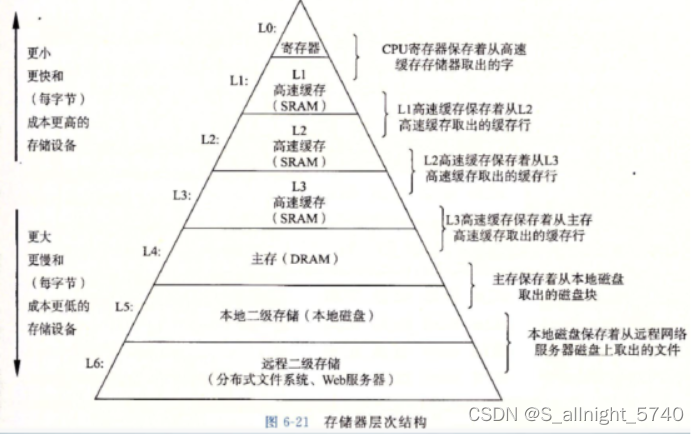
数据结构:堆的简单介绍
目录 堆的介绍:(PriorityQueue) 大根堆:根节点比左右孩子节点大 小根堆:根节点比左右孩子节点小 堆的存储结构: 为什么二叉树在逻辑上用满二叉树结构,而不是普通二叉树呢? 因为如果是普通二叉树会造成资源的浪费编辑 堆的介绍:(PriorityQueue) 堆又称优先级队列,何为优先…...
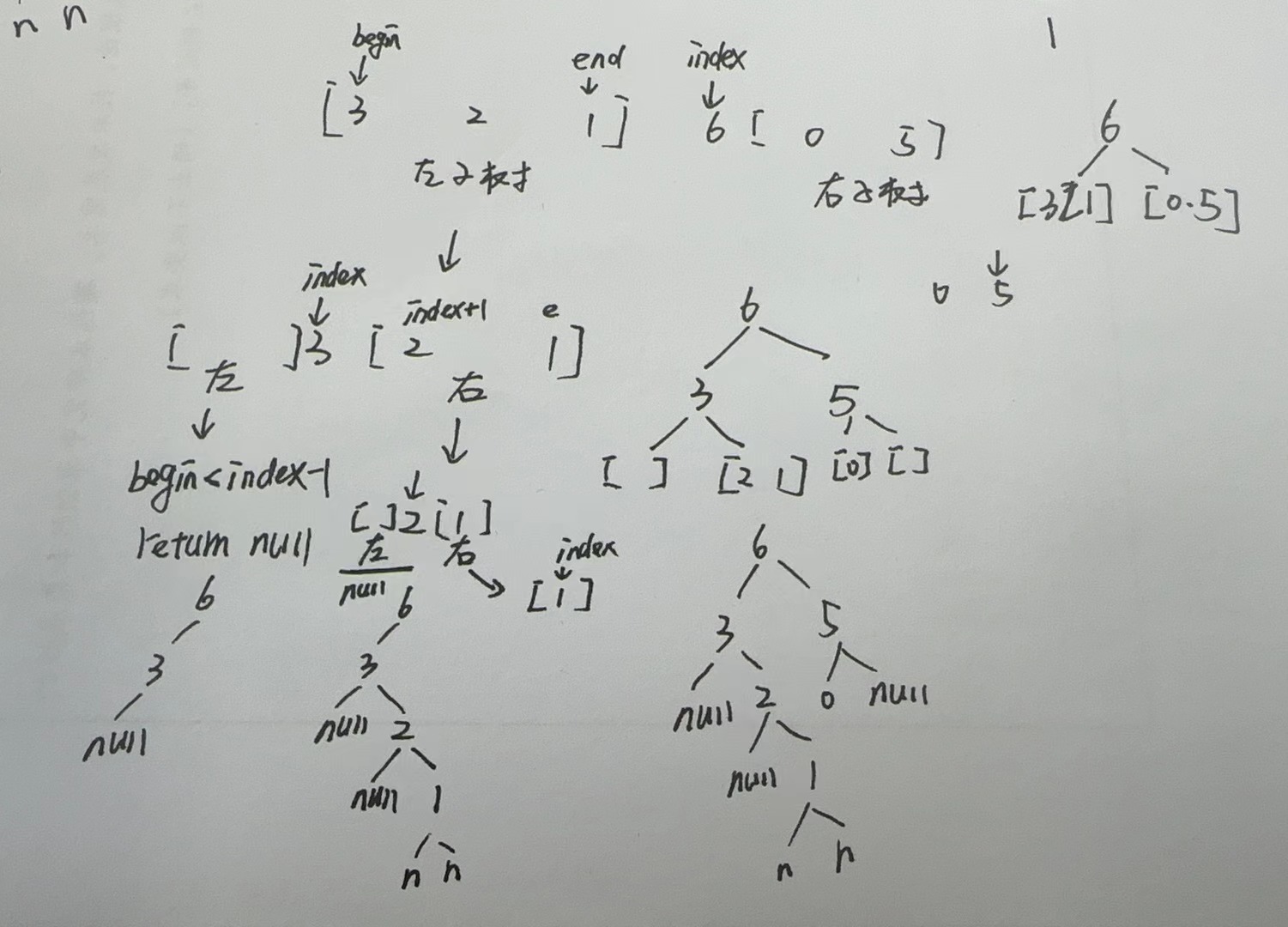
【LeetCode-中等题】654.最大二叉树
文章目录 题目方法一:递归 题目 方法一:递归 class Solution {int[] num null; public TreeNode constructMaximumBinaryTree(int[] nums) {num nums;return myTree(0,num.length-1);}public TreeNode myTree( int begin , int end){if(begin > end…...

基于微信小程序的刷题考试系统设计与实现(适用于各类考试类、答题类程序)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
