树莓集团又一力作,打造天府蜂巢成都直播产业园样板工程
树莓集团再次推出惊艳之作,以打造成都天府蜂巢直播产业园为目标。该基地将充分展现成都直播产业园的巨大潜力与无限魅力,成为一个真正的产业园样板工程。

强强联手 打造未来
成都天府蜂巢直播产业园位于成都科学城兴隆湖高新技术服务产业园内,是天府新区成都直管区的重要发展区域。占地面积广阔,环境优美。生态环伺,落实公园城市建设理念,便捷交通,城际城内交通通达四方。树莓集团与上市公司德商产投展望成都直播产业园的发展前景,决定强强联手打造直播领域数字经济IP,以双方优势与渠道资源,精心打造成都天府蜂巢直播产业园。树莓集团相信,未来将成都天府蜂巢直播产业园建设成一个产业链完整、功能齐全的综合性园区,必将成为直播产业的新引擎。

成熟配套 全维赋能
成都天府蜂巢直播产业园将提供全方位的支持与服务,为直播从业者提供先进的设施与设备,以及高效的运营管理体系。园区将配备先进的直播设备,包括高清摄像机、灯光和音响设备,以及网络加速器和云服务等先进技术。这些设施将帮助直播从业者提供更高质量的直播内容,并提升用户体验。

另外,成都天府蜂巢直播产业园还将提供专业培训和技术支持,帮助直播从业者提升技巧和能力。园区内将设立培训教室和实践工作室,引进优秀的直播导师和行业专家,为从业者提供全面的培训课程和指导。这将有助于打造一支专业化、创新性强的直播团队,推动直播产业的快速发展。

加强合作 促进发展
成都天府蜂巢直播产业园不仅仅是一个生产、学习的场所,更是一个创新的汇聚地。园区将举办各种直播行业的培训、论坛和研讨会等活动,邀请国内的行业精英和专家学者共同交流思想,分享经验。这将加强直播产业间的合作,促进产业的健康发展。

树莓集团致力于推动成都直播产业的发展,通过打造成都直播产业园,将直播产业带入一个新的高度。相信随着该园的建设与运营,成都直播产业园将迎来更广阔的发展空间,为入驻企业创造更多机遇和价值。树莓集团将继续投入资源和精力,为成都直播产业的蓬勃发展贡献力量。
相关文章:

树莓集团又一力作,打造天府蜂巢成都直播产业园样板工程
树莓集团再次推出惊艳之作,以打造成都天府蜂巢直播产业园为目标。该基地将充分展现成都直播产业园的巨大潜力与无限魅力,成为一个真正的产业园样板工程。 强强联手 打造未来 成都天府蜂巢直播产业园位于成都科学城兴隆湖高新技术服务产业园内࿰…...

ubuntu 软件包管理之二制作升级包
Deb 包(Debian 软件包)是一种用于在 Debian 及其衍生发行版(例如 Ubuntu)中分发和安装软件的标准包装格式。它们构成了 Debian Linux 发行版中的软件包管理系统的核心组成部分,旨在简化软件的分发、安装、更新和卸载流程。在本篇文章中,我们将深入探讨以下内容: Deb 包基…...
)
TCP/IP网络江湖——数据链路层的防御招式(数据链路层下篇:数据链路层的安全问题)
目录 引言 一、 数据链路层的隐私与保密 二、数据链路层的安全协议与加密...

ios项目安装hermes-engine太慢问题
问题说明 ios工程,在使用"pod install"安装依赖的时候,由于超时总是报错 $ pod install ... Installing hermes-engine (0.71.11)[!] Error installing hermes-engine [!] /usr/bin/curl -f -L -o /var/folders/4c/slcchpy55s53ysmz_1_q_gzw…...
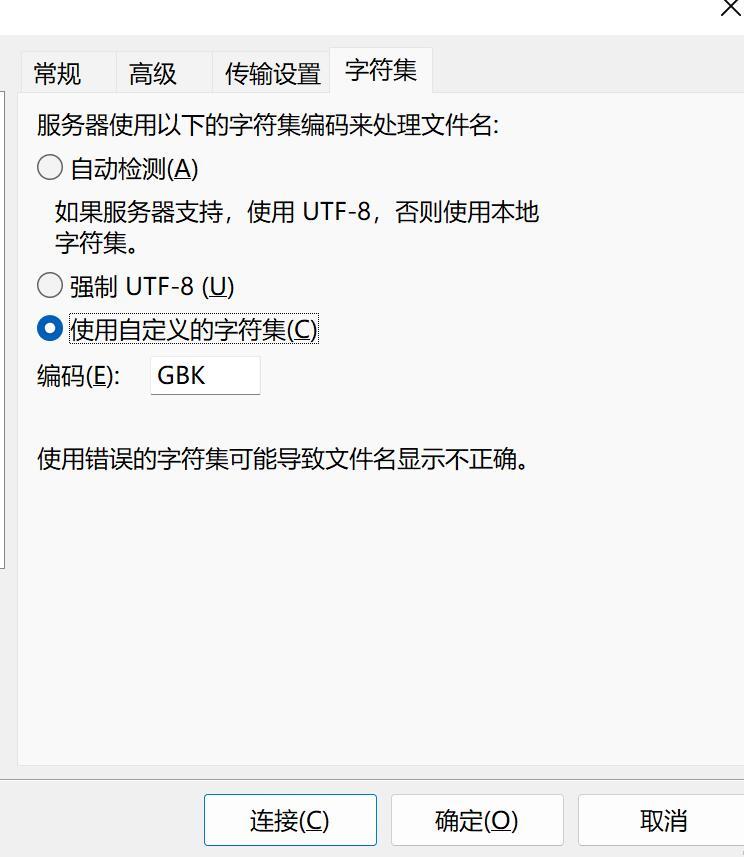
构建个人云存储:本地电脑搭建SFTP服务器,开启公网访问,轻松共享与管理个人文件!
本地电脑搭建SFTP服务器,并实现公网访问 文章目录 本地电脑搭建SFTP服务器,并实现公网访问1. 搭建SFTP服务器1.1 下载 freesshd 服务器软件1.3 启动SFTP服务1.4 添加用户1.5 保存所有配置 2. 安装SFTP客户端FileZilla测试2.1 配置一个本地SFTP站点2.2 内…...

springboot 下载文件为excel数据,中文自定义单元格宽度
/**2 * Description:表格自适应宽度(中文支持)3 * Author: 4 * param sheet sheet5 * param columnLength 列数6 */7 private static void setSizeColumn(HSSFSheet sheet, int columnLength) {8 for (int columnNum 0; columnNum < …...

机器学习 面试/笔试题
1. 生成模型 VS 判别模型 生成模型: 由数据学得联合概率分布函数 P ( X , Y ) P(X,Y) P(X,Y),求出条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)的预测模型。 朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型(LDA)、限制玻尔兹曼机…...

某企查ymg_ssr列表详情
js篇— 今天来看下某企查的列表详情–侵删 header发现这个参数 先断点一下 然后上一步 就到了这个地方 就开始扣一下这个js 三大段,先不解混淆了, 给a粘贴出来 ,去掉自执行 给结果稍微改一下 缺windows,开始补环境 直接上…...

使用YOLOv5的backbone网络识别图像天气 - P9
目录 环境步骤环境设置包引用声明一个全局的设备 数据准备收集数据集信息构建数据集在数据集中读取分类名称划分训练、测试数据集数据集划分批次 模型设计编写维持卷积前后图像大小不变的padding计算函数编写YOLOv5中使用的卷积模块编写YOLOv5中使用的Bottleneck模块编写YOLOv5…...

TikTok海外扩张:亚马逊的新对手崛起
随着社交媒体和电子商务的融合,TikTok正迅速崭露头角,成为亚马逊等传统电商巨头的潜在竞争对手。这一新兴平台的快速发展引发了广泛的关注,特别是在全球范围内。 在这篇文章中,我们将探讨TikTok海外扩张的战略,以及它…...
CSS详细基础(五)选择器的优先级
本节介绍选择器优先级,优先级决定了元素最终展示的样式~ 浏览器是通过判断CSS优先级,来决定到底哪些属性值是与元素最为相关的,从而作用到该元素上。CSS选择器的合理组成规则决定了优先级,我们也常常用选择器优先级来合理控制元素…...

LLM-TAP随笔——有监督微调【深度学习】【PyTorch】【LLM】
文章目录 5、 有监督微调5.1、提示学习&语境学习5.2、高效微调5.3、模型上下文窗口扩展5.4、指令数据构建5.5、开源指令数据集 5、 有监督微调 5.1、提示学习&语境学习 提示学习 完成预测的三个阶段:提示添加、答案搜索、答案映射 提示添加 “[X] 我感到…...
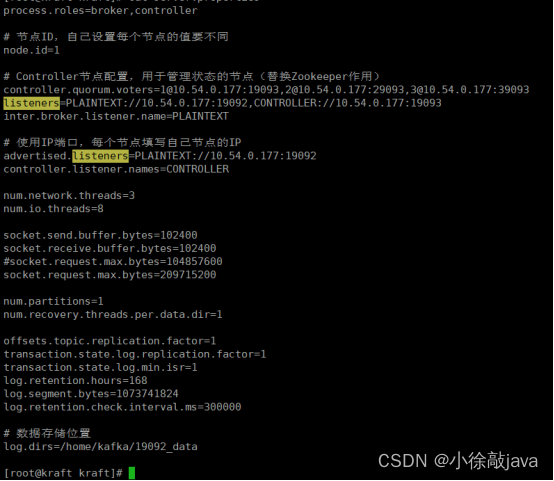
kafka伪集群部署,使用docker环境拷贝模式
线上启动容器的方式是复制容器的运行环境出来,然后进行运行脚本的形式 1:在home/kafka目录下创建如下目录 2:复制kafka1容器内的数据/bitnami/kafka/data,直接放在1992_data里面,同理,复制kafka2容器内的数据/bitnami/…...

工业交换机一般的价格是多少呢?
工业交换机是一种应用于工业领域的网络设备。它的性能和所有安全指标都比一般商业交换机更加稳定。所以,工业级交换机的价格相对于普通的交换机要稍稍昂贵一些。工业交换机一般的价格是多少呢?每个厂家的交换机价格是不是都一样呢? 首先&…...

QT使用前的知识
QT使用前的知识 常用的快捷键 源文件的内容解释 .pro文件的解释 头文件的解释 构建新的对象—组成对象树 槽函数 自定的信号和槽 槽函数的信号是一个重载函数时 电机按钮触发信号 调用无参数的信号 断开信号...

Unity制作旋转光束
Unity制作旋转光束 大家好,我是阿赵。 这是一个在很多游戏里面可能都看到过的效果,在传送门、魔法阵、角色等脚底下往上散发出一束拉丝形状的光,然后在不停的旋转。 这次来在Unity引擎里面做一下这种效果。 一、准备材料 需要准备的素材很简…...

考研王道强化阶段(二轮复习)“算法题”备考打卡表 记录
问题:做408真题_2010_42题,即王道书 2.2.3_大题_10 思路: 回头补 代码: int moveL(SqlList &L,SqlList &S,int p) {// 健壮性表达if( L.len 0 ){return 0;}// 调用另外一个顺序表存储pos前面的元素for( int i0;i<p;…...

UE4/5数字人MetaHuman通过已有动画进行修改
目录 通过已有动画修改动画 开始制作 创建一个关卡序列 将动画序列烘焙到控制绑定 打开我们自己创建的动画序列 之后便是烘焙出来 通过已有动画修改动画 首先架设我们已经有相关的MetaHuman的动画,但是这个动画因为是外部导入进来的,所以可能会出…...

在Mac M2本地注册GitLab runner
最近在搞公司的CI/CD,简单记录下部分过程 安装runner sudo curl --output /usr/local/bin/gitlab-runner "https://gitlab-runner-downloads.s3.amazonaws.com/latest/binaries/gitlab-runner-darwin-arm64" 创建runner 这个步骤需要在gitlab中进行&am…...

「大数据-2.2」使用命令操作HDFS文件系统
目录 一、HDFS文件系统基本信息 1. HDFS的路径表达形式 2.HDFS和Linux的根目录的区分 二、 使用命令操作HDFS文件系统 0. Hadoop的两套命令体系 1. 创建文件夹 2. 查看指定目录下内容 3. 上传文件到HDFS指定目录下 4. 查看HDFS文件内容 5. 下载HDFS文件 6. 拷贝HDFS文件 7.…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
