leetCode 123.买卖股票的最佳时机 III 动态规划 + 状态压缩
123. 买卖股票的最佳时机 III - 力扣(LeetCode)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1] 输出:0
>>思路和分析
这道题目相对leetCode 121.买卖股票的最佳时机 和 leetCode 122.买卖股票的最佳时机 II难了不少。关键在于至多买卖几次,意味着可以买卖一次,可以买卖两次,也可以不买卖。
>>动规五部曲
1.确定dp数组以及下标的含义
一天 一共有 5 个 状态 ,dp[i][j] 中 i 表示 第 i 天,j 为[0 - 4] 五个状态,dp[i][j]表示第 i 天状态 j所剩最大现金
- 0.没有操作(其实也可以不设置这个状态)
- 1.第一次持有股票
- 2.第一次不持有股票
- 3.第二次持有股票
- 4.第二次不持有股票
"持有" : 不代表就是当天"买入"!可能昨天就买入了,今天保持有的状态
2.确定递推公式
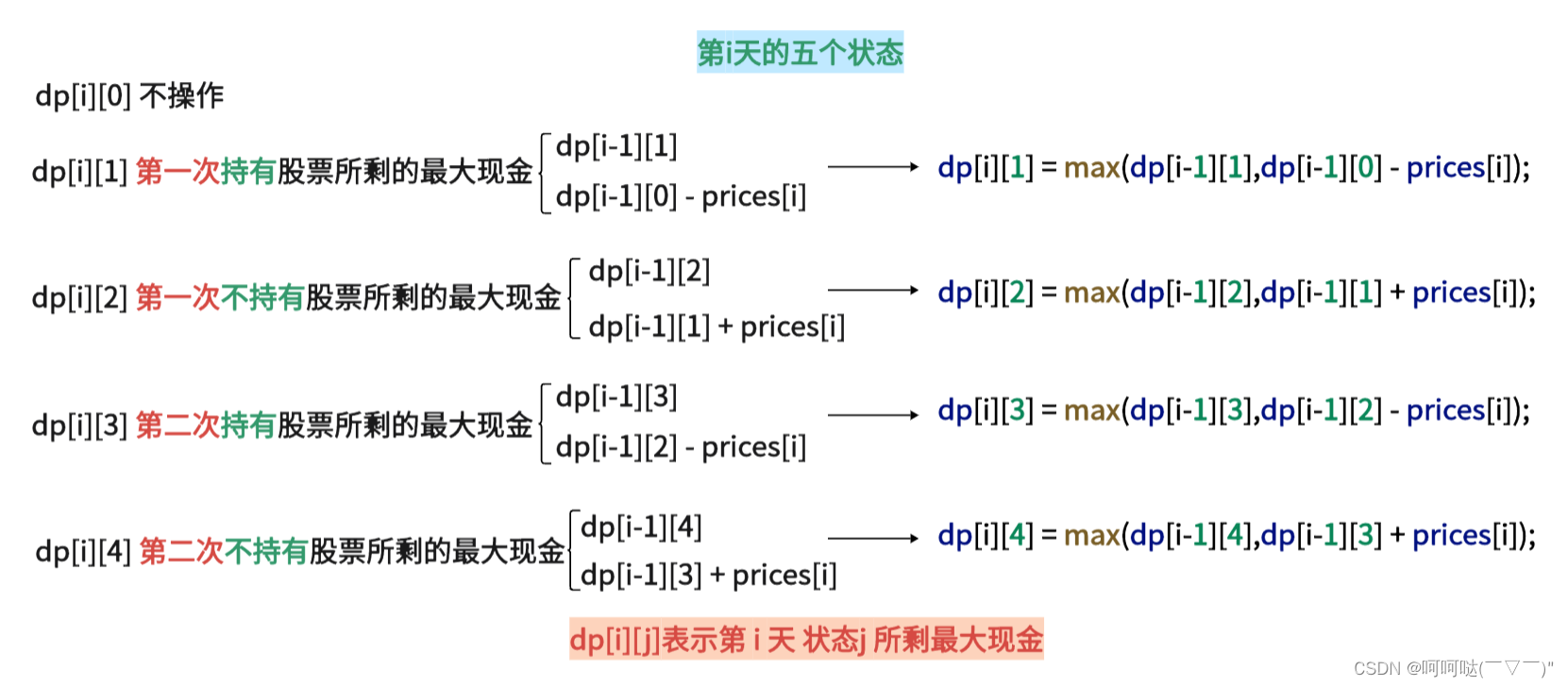
3.dp数组初始化
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
dp[0][3] = -prices[0];
dp[0][4] = 0;4.确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值
5.举例推导dp数组
以输入[1,2,3,4,5]为例
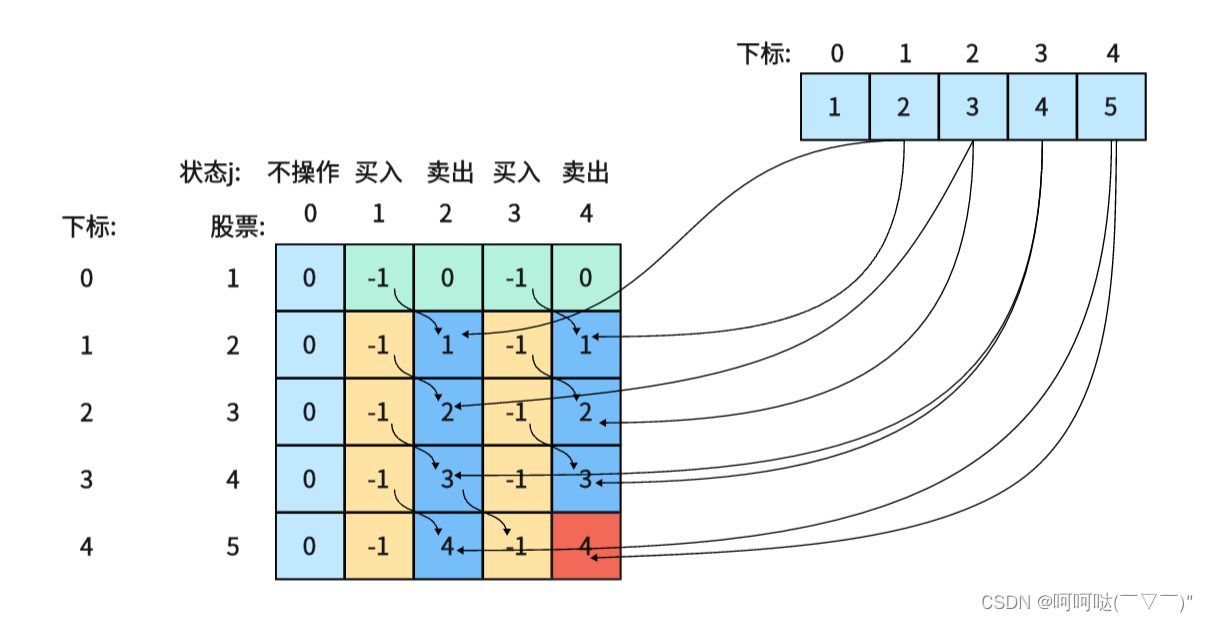
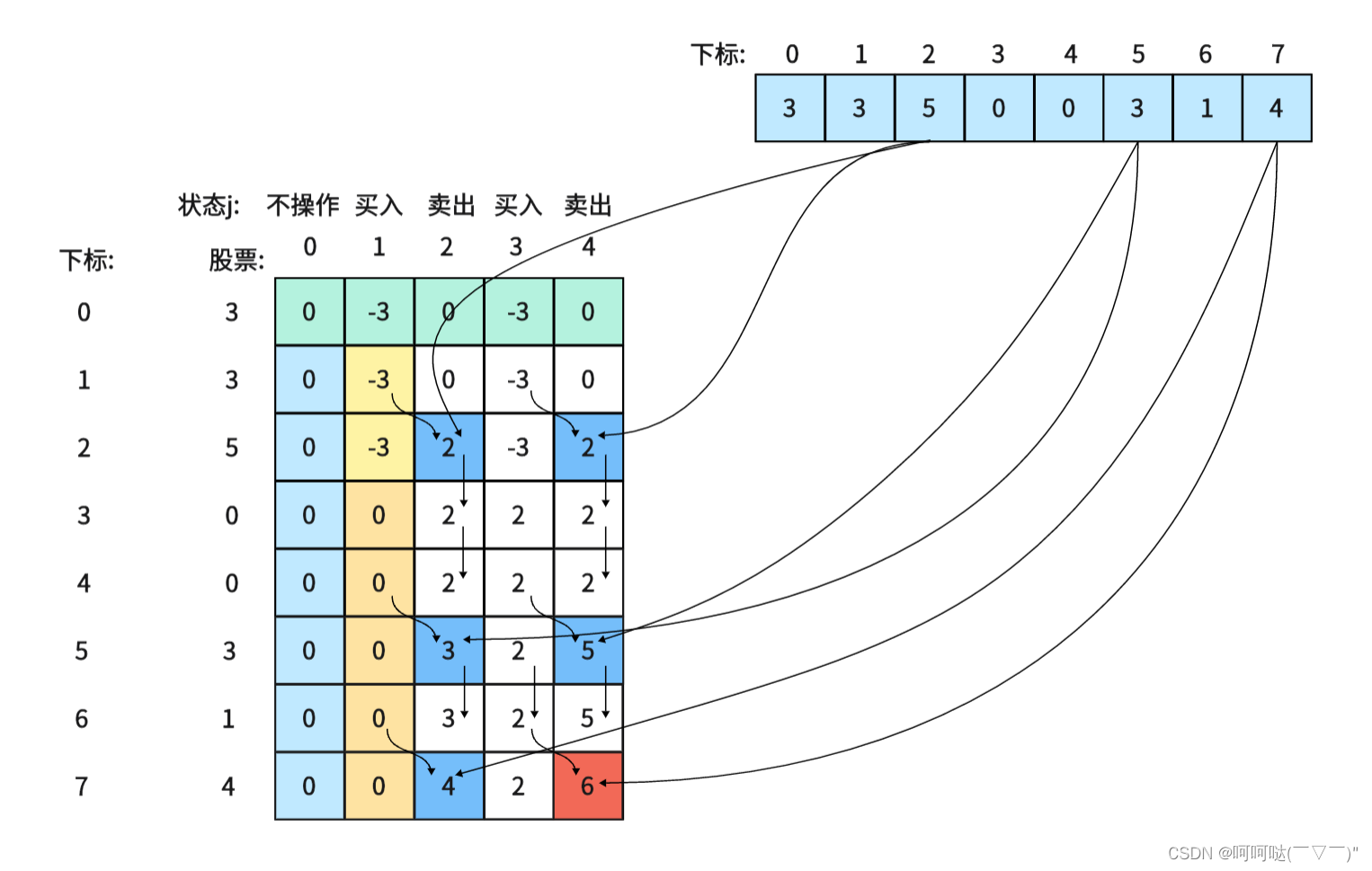
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();if (len == 0) return 0;vector<vector<int>> dp(len, vector<int>(5, 0));dp[0][1] = -prices[0];dp[0][3] = -prices[0];for (int i = 1; i < len; i++) {// dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[len - 1][4];}
};其实可以不设置,‘0. 没有操作’ 这个状态,因为没有操作,手上的现金自然就是0, 正如在 leetCode 121.买卖股票的最佳时机和 leetCode 122.买卖股票的最佳时机 II也没有设置这一状态是一样的。
- 时间复杂度:O(n)
- 空间复杂度:O(n × 4)
>>状态压缩
摘取自代码随想录代码随想录 (programmercarl.com):
- dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1],即保持买入股票的状态,那么 dp[2] = max(dp[2], dp[1] + prices[i]);中dp[1] + prices[i] 就是今天卖出。
- 如果dp[1]取dp[0] - prices[i],今天买入股票,那么dp[2] = max(dp[2], dp[1] + prices[i]);中的dp[1] + prices[i]相当于是今天再卖出股票,一买一卖收益为0,对所得现金没有影响。相当于今天买入股票又卖出股票,等于没有操作,保持昨天卖出股票的状态了。
// 状态压缩
class Solution {
public:int maxProfit(vector<int>& prices) { if(prices.size() == 0) return 0; int len = prices.size();vector<int> dp(5,0);dp[1] = -prices[0];dp[3] = -prices[0];for(int i=1;i<len;i++) {dp[1] = max(dp[1],dp[0] - prices[i]);dp[2] = max(dp[2],dp[1] + prices[i]);dp[3] = max(dp[3],dp[2] - prices[i]);dp[4] = max(dp[4],dp[3] + prices[i]);}return dp[4];}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
参考和推荐文章、视频
代码随想录 (programmercarl.com)
动态规划,股票至多买卖两次,怎么求? | LeetCode:123.买卖股票最佳时机III_哔哩哔哩_bilibili
来自代码随想录课堂截图:

相关文章:

leetCode 123.买卖股票的最佳时机 III 动态规划 + 状态压缩
123. 买卖股票的最佳时机 III - 力扣(LeetCode) 给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意:你不能同时参与多笔交易࿰…...

JavaScript计算两个时间相差多少个小时的封装函数
js中计算两个时间相差小时数 在JavaScript中,你可以使用Date对象来处理日期和时间。下面是一个函数,它接受两个时间字符串作为参数,并返回两者之间的时间差(以小时为单位): function calculateHours(time…...
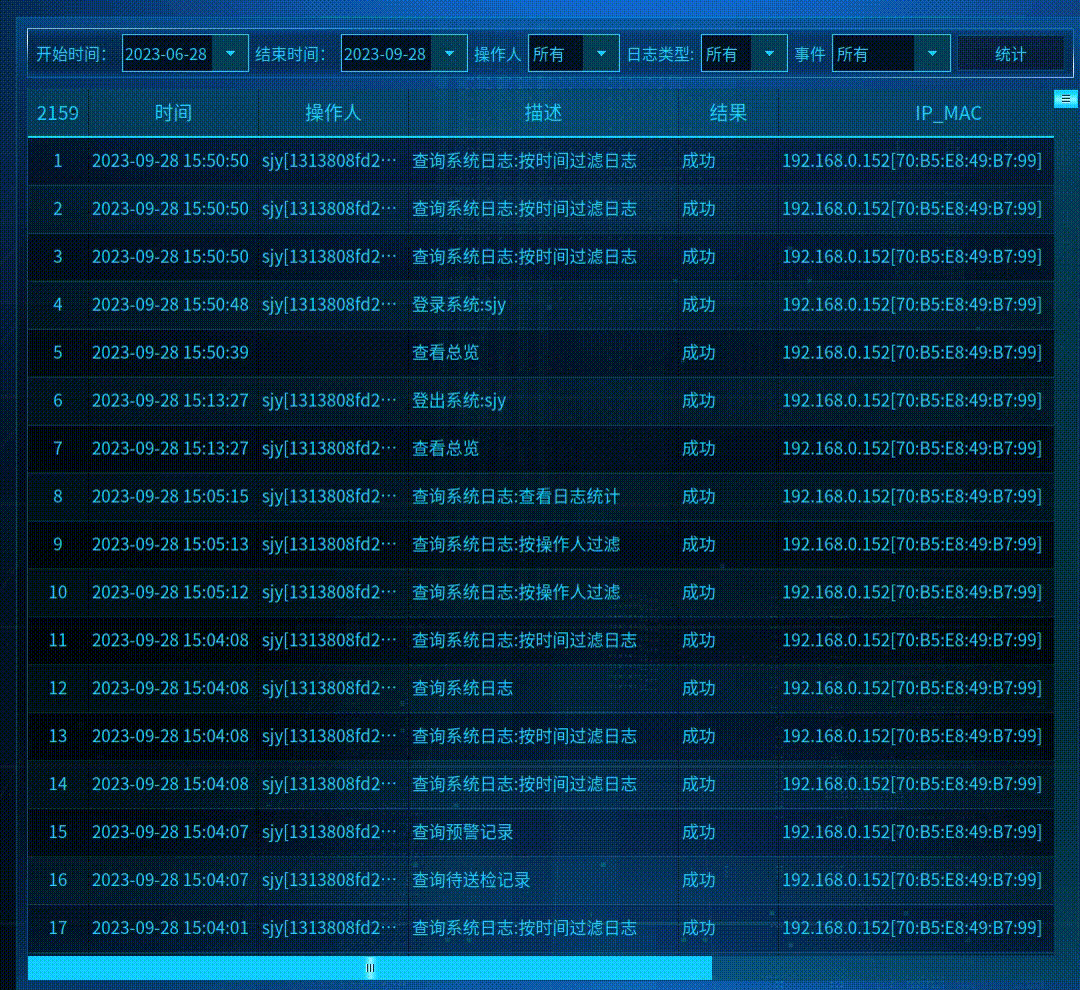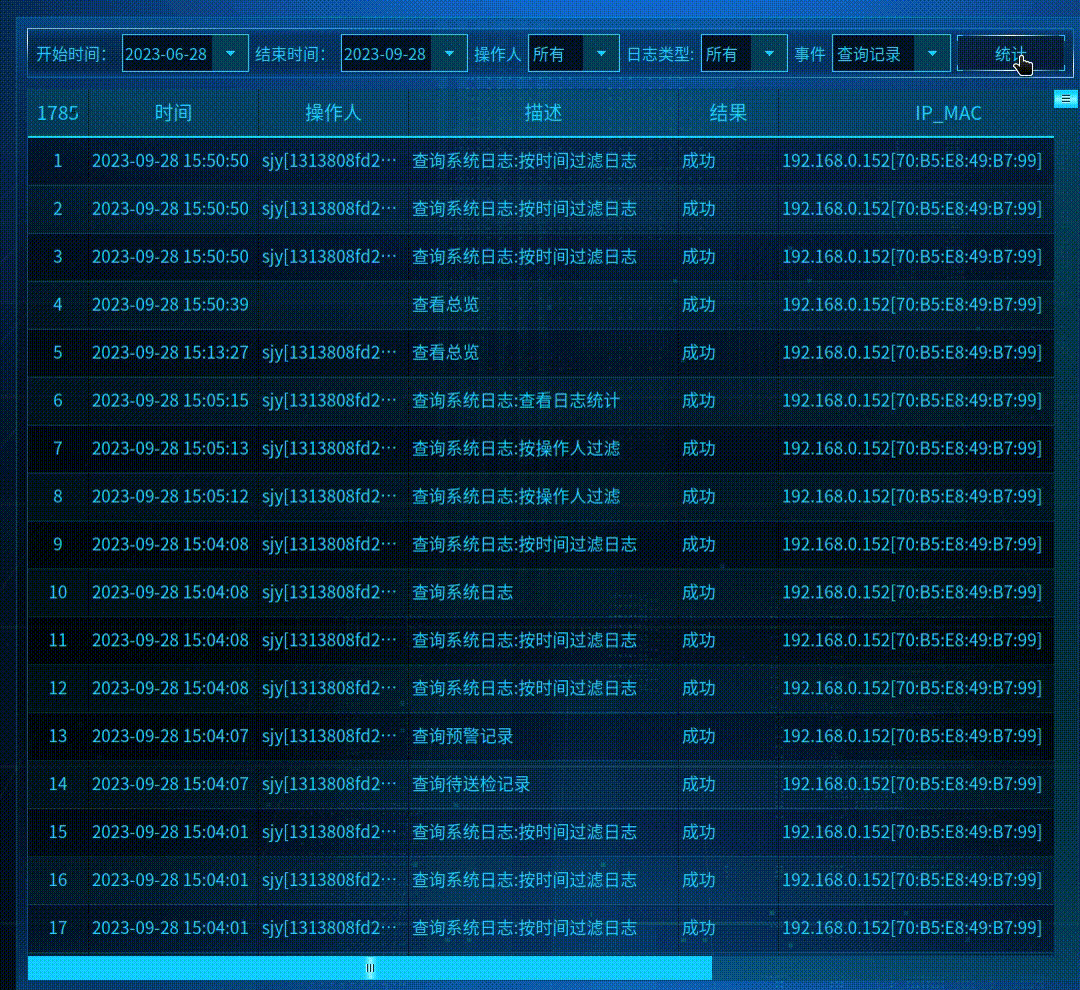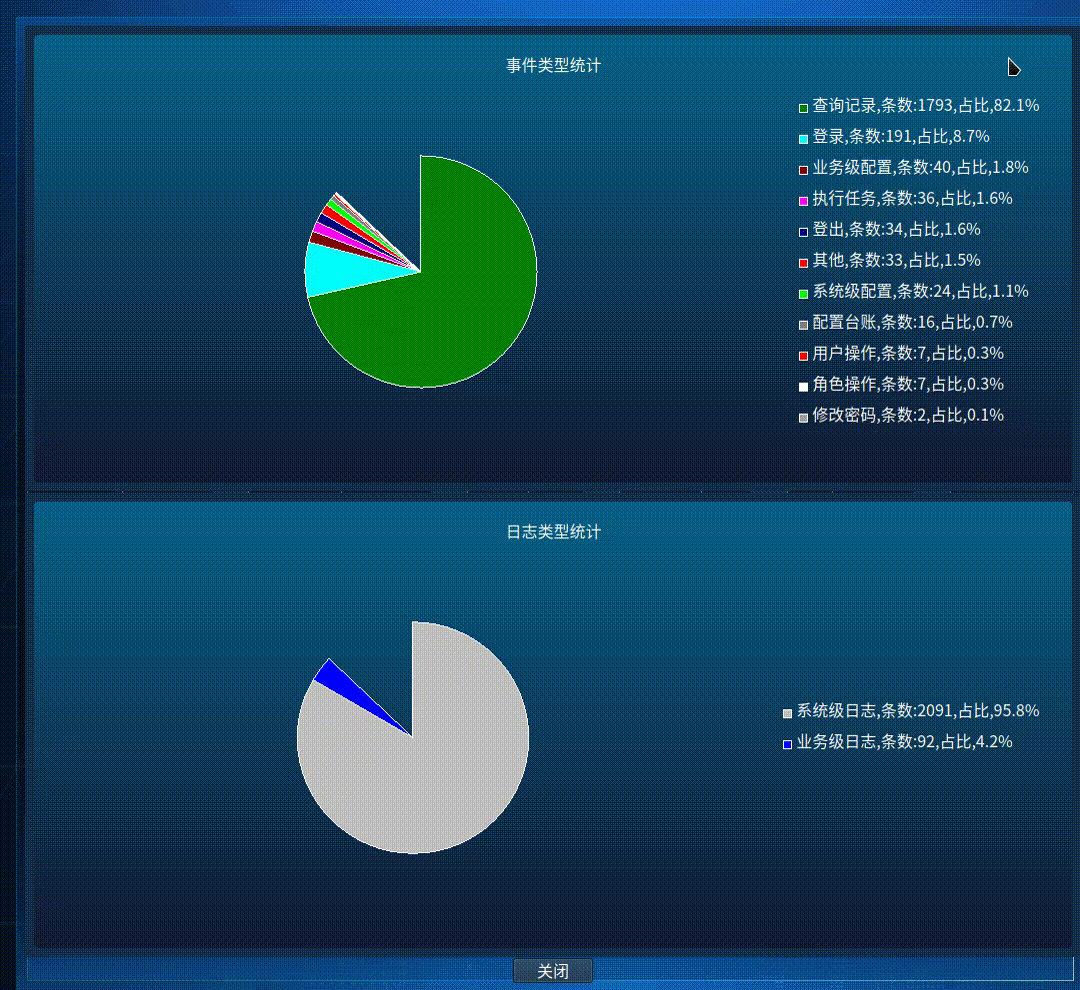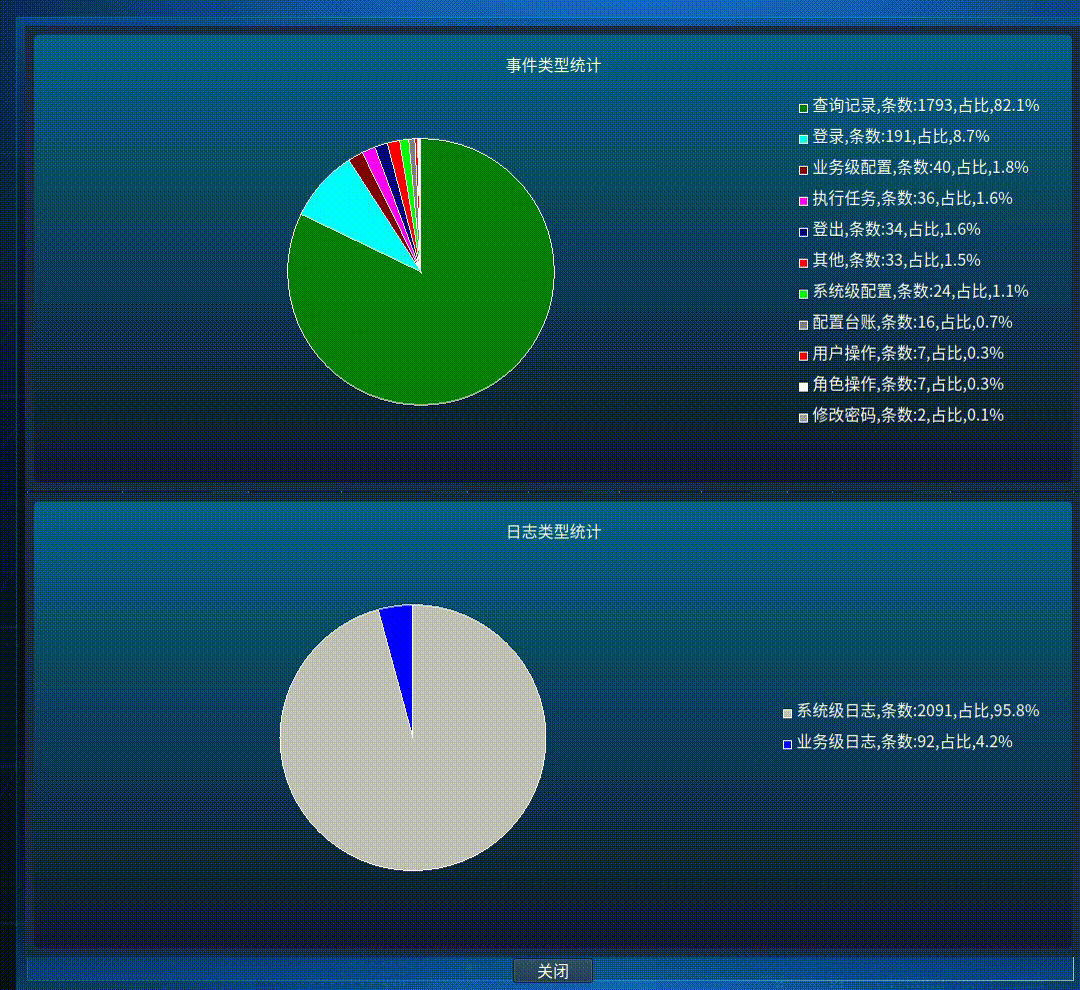
Qt 画自定义饼图统计的例子
先给出结果图,这个例子是将各种事件分类然后统计的其比例,然后画饼图显示出来 这个是我仿照官方给的例子,让后自己理解后,修改的,要生成饼图,需要QT的 charts 支持,安装QT 没有选择这个的&#…...
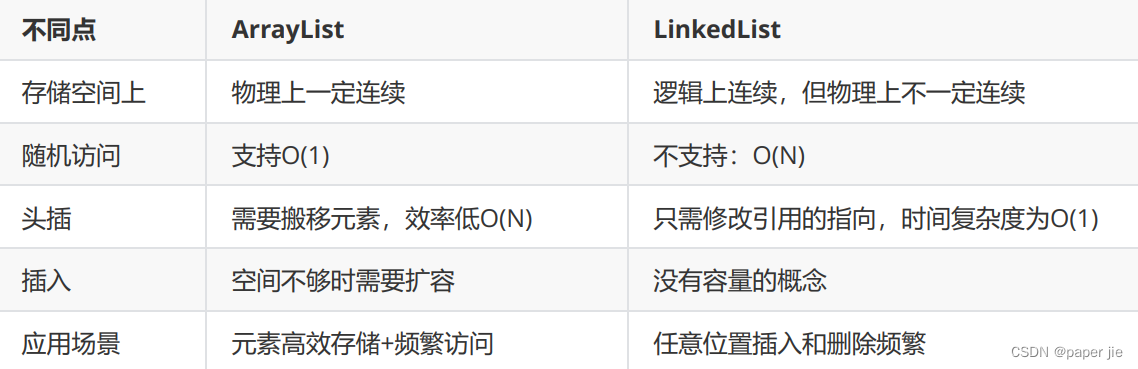
【数据结构】链表与LinkedList
作者主页:paper jie 的博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《JAVA数据结构》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精…...

Flink RoaringBitmap去重
1、RoaringBitmap的依赖 <!-- 去重大哥--> <dependency><groupId>org.roaringbitmap</groupId><artifactId>RoaringBitmap</artifactId><version>0.9.21</version> </dependency> 2、Demo去重 package com.gwm.driver…...
Elasticsearch—(MacOs)
1⃣️环境准备 准备 Java 环境:终端输入 java -version 命令来确认版本是否符合 Elasticsearch 要求下载并解压 Elasticsearch:前往(https://www.elastic.co/downloads/elasticsearch)选择适合你的 Mac 系统的 Elasticsearch 版本…...

插入排序与希尔排序
个人主页:Lei宝啊 愿所有美好如期而遇 前言: 这两个排序在思路上有些相似,所以有人觉得插入排序和希尔排序差别不大,事实上,他们之间的差别不小,插入排序只是希尔排序的最后一步。 目录 前言:…...
C# OpenCvSharp 基于直线检测的文本图像倾斜校正
效果 项目 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using OpenCvSharp;namespace OpenCvSharp_基于直线检测的文…...

“智慧时代的引领者:探索人工智能的无限可能性“
目录 一.背景 二.应用 2.1金融领域 2.2医疗领域 2.3教育领域 三.发展 四.总结: 一.背景 人工智能(Artificial Intelligence,简称AI),是指通过计算机程序模拟人类智能的一种技术。它是计算机科学、工程学、语言学、哲学等多…...
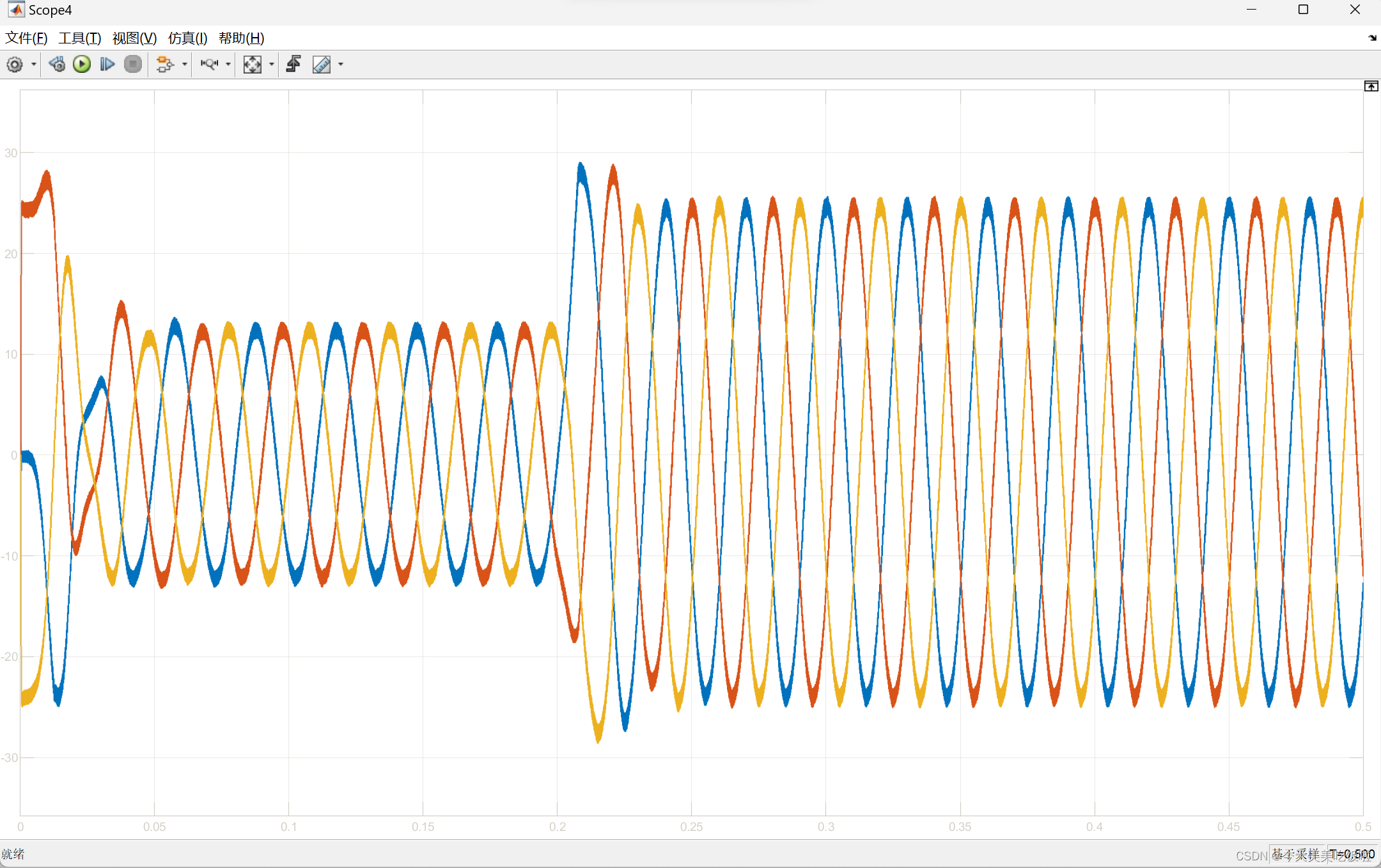
PMSM——转子位置估算基于QPLL
文章目录 前言仿真模型观测器速度观测位置观测转矩波形电流波形 前言 今后是电机控制方向的研究生的啦,期待有同行互相交流。 仿真模型 观测器 速度观测 位置观测 转矩波形 电流波形...

Android Studio之Gradle和Gradle插件的区别
解释的很详细 Android Studio之Gradle和Gradle插件的区别...
DataExcel控件读取和保存excel xlsx 格式文件
需要引用NPOI库 https://github.com/dotnetcore/NPOI 调用Read 函数将excel读取到dataexcel控件 调用Save 函数将dataexcel控件文件保存为excel文件 using NPOI.HSSF.UserModel; using NPOI.HSSF.Util; using NPOI.SS.UserModel; using NPOI.SS.Util; using System; using …...

【JavaEE】CAS(Compare And Swap)操作
文章目录 什么是 CASCAS 的应用如何使用 CAS 操作实现自旋锁CAS 的 ABA 问题CAS 相关面试题 什么是 CAS CAS(Compare and Swap)是一种原子操作,用于在无锁情况下保证数据一致性的问题。它包含三个操作数——内存位置、预期原值及更新值。在执…...
)
第三章:最新版零基础学习 PYTHON 教程(第三节 - Python 运算符—Python 中的关系运算符)
关系运算符用于比较值。它根据条件返回 True 或 False。这些运算符也称为比较运算符。 操作员描述 句法> 大于:如果左操作数大于右操作数,则为 Truex > y...
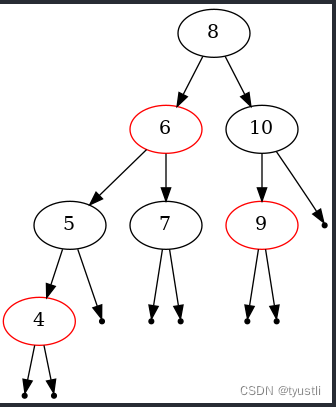
【GDB】使用 GDB 自动画红黑树
阅读本文前需要的基础知识 用 python 扩展 gdb python 绘制 graphviz 使用 GDB 画红黑树 前面几节中介绍了 gdb 的 python 扩展,参考 用 python 扩展 gdb 并且 python 有 graphviz 模块,那么可以用 gdb 调用 python,在 python 中使用 grap…...

使用Vue3+elementPlus的Tree组件实现一个拖拽文件夹管理
文章目录 1、前言2、分析3、实现4、踩坑4.1、拖拽辅助线的坑4.2、数据的坑4.3、限制拖拽4.4、样式调整 1、前言 最近在做一个文件夹管理的功能,要实现一个树状的文件夹面板。里面包含两种元素,文件夹以及文件。交互要求如下: 创建、删除&am…...
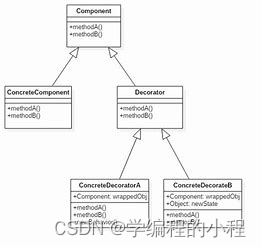
小谈设计模式(7)—装饰模式
小谈设计模式(7)—装饰模式 专栏介绍专栏地址专栏介绍 装饰模式装饰模式角色Component(抽象组件)ConcreteComponent(具体组件)Decorator(抽象装饰器)ConcreteDecorator(具…...

nginx 多层代理 + k8s ingress 后端服务获取客户真实ip 配置
1.nginx http 七层代理 修改命令空间: namespace: nginx-ingress : configmap:nginx-configuration kubectl get cm nginx-configuration -n ingress-nginx -o yaml添加如上配置 compute-full-forwarded-for: “true” forwarded-for-header: X-Forwa…...

6种最常用的3D点云语义分割AI模型对比
由于增强现实/虚拟现实的发展及其在计算机视觉、自动驾驶和机器人领域的广泛应用,点云学习最近引起了人们的关注。 深度学习已成功用于解决 2D 视觉问题,然而,由于其处理面临独特的挑战,深度学习技术在点云上的使用仍处于起步阶段…...
-获取UI中选择对象的handle值)
UG NX二次开发(C#)-获取UI中选择对象的handle值
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、设计一个简单的UI界面3、创建工程项目4、测试结果1、前言 我在哔哩哔哩的视频中看到有人问我如何获取UI选择对象的Handle,本来想把Tag、Taggedobject、Handle三者的关系讲一下,然后看…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
