【蓝桥杯集训·每日一题】AcWing 2058. 笨拙的手指
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 哈希表
- 秦九韶算法
一、题目
1、原题链接
2058. 笨拙的手指
2、题目描述
奶牛贝茜正在学习如何在不同进制之间转换数字。
但是她总是犯错误,因为她无法轻易的用两个前蹄握住笔。
每当贝茜将数字转换为一个新的进制并写下结果时,她总是将其中的某一位数字写错。
例如,如果她将数字 14 转换为二进制数,那么正确的结果应为 1110,但她可能会写下 0110 或 1111 。
贝茜不会额外添加或删除数字,但是可能会由于写错数字的原因,写下包含前导 0 的数字。
给定贝茜将数字 N 转换为二进制数字以及三进制数字的结果,请 确定 N 的正确初始值(十进制表示)。
输入格式
第一行包含 N 的二进制表示,其中一位是错误的。
第二行包含 N 的三进制表示,其中一位是错误的。
输出格式
输出正确的 N 的值。
数据范围
0≤N≤109,且存在唯一解。
输入样例:
1010 212输出样例:
14样例解释
14 在二进制下的正确表示为 1110,在三进制下的正确表示为 112。
二、解题报告
1、思路分析
思路来源:y总视频讲解
y总yyds
(1)将数N的二进制表示下可能写错的每种情况的十进制下的数值存入哈希表中。
(2)将数N的三进制表示下的每种写错的情况的十进制下的数值在哈希表中进行查找,如果该数值出现过,则该数就是N的十进制表示,输出即可。
2、时间复杂度
时间复杂度为O(n)
3、代码详解
使用STL中unordered_set
#include <iostream>
#include <string>
#include <unordered_set>
using namespace std;
//使用秦九韶算法,将y进制下的数x转化为十进制
int ten(string x,int y){int ans=0;for(int i=0;i<x.size();i++){ans=ans*y+x[i]-'0';}return ans;
}
int main(){string n,m;cin>>n>>m;unordered_set<int> s;for(int i=0;i<n.size();i++){string t=n;t[i]^=1; //改变第i位数,0变1,1变0if(t[0]=='0'&&t.size()>1) continue; //如果数字存在前导0,则不合法,直接跳过s.insert(ten(t,2)); //将写错后的数字在十进制下的数值放入哈希表}for(int i=0;i<m.size();i++){for(int j=0;j<3;j++){ //枚举第i位数字可能的写错情况,然后再在哈希表中查找该数的十进制下数值是否出现过if(m[i]-'0'!=j){ string tmp=m;tmp[i]=j+'0';if(tmp[0]=='0'&&tmp.size()>1) continue; //同上if(s.count(ten(tmp,3))){ //如果该数的十进制的值在哈希表存在过,直接输出,该数就是答案cout<<ten(tmp,3);}}}}return 0;
}
手写哈希表
#include <iostream>
#include <string>
#include <cstring>
using namespace std;
const int N=103;
int h[N];
//哈希表开放寻址法,如果x存在,返回x的位置,否则返回x应该插入的位置
int find(int x){int t=(x%N+N)%N;while(h[t]!=-1&&h[t]!=x){t++;if(t==N) t=0;}return t;
}
//使用秦九韶算法,将y进制下的数x转化为十进制
int ten(string x,int y){int ans=0;for(int i=0;i<x.size();i++){ans=ans*y+x[i]-'0';}return ans;
}int main(){string n,m;cin>>n>>m;memset(h,-1,sizeof h);for(int i=0;i<n.size();i++){string t=n;t[i]^=1; //改变第i位数,0变1,1变0if(t[0]=='0'&&t.size()>1) continue; //如果数字存在前导0,则不合法,直接跳过h[find(ten(t,2))]=ten(t,2); //将写错后的数字在十进制下的数值放入哈希表}for(int i=0;i<m.size();i++){for(int j=0;j<3;j++){ //枚举第i位数字可能的写错情况,然后再在哈希表中查找该数的十进制下数值是否出现过if(m[i]-'0'!=j){ string tmp=m;tmp[i]=j+'0';if(tmp[0]=='0'&&tmp.size()>1) continue; //同上if(h[find(ten(tmp,3))]!=-1){ //如果该数的十进制的值在哈希表存在过,直接输出,该数就是答案cout<<ten(tmp,3);}}}}return 0;
}
三、知识风暴
哈希表
- 哈希表的增删改查的时间复杂度为O(1)。
- C++中STL的
unordered_set和unordered_map底层就是使用哈希结构实现的。秦九韶算法
- 参考百度百科
秦九韶算法是一种多项式的简化算法。
具体做法是将多项式
改写为:
先计算内层的数值然后依次由内向外进行拓展。- 针对本题我们可以使用其来进行计算不同进制转十进制的结果。
例如:求二进制1010的十进制
二进制1010转换为10进制的算式可以写成1x23+0x22+1x21+0x20,类比上述多项式,2即为多项式中的x,二进制的每位数字则是多项式的系数,而我们在本题中二进制数是按字符串(记为s)读入的,所以将其每位数字记为s[i]。根据上述算法可知,我们最终算的每层均是s[i]*x+s[i+1],而在计算下一层时,上一层的结果更新成了下一层x前面的系数,所以我们将上一层的结果记录到临时变量ans中,然后按照公式s[i]*x+s[i+1]依次向外扩展,直到遍历完所有数字,ans就是多项式的值,也就是我们要求的十进制的数值。所以据此我们可以总结出计算本题将
x进制转换为十进制数值的代码int ans=0; //ans存储每层的结果,最终ans的值为最外层的值,也就是多项式的值 for(int i=0;i<s.size();i++){ans=ans*x+s[i]-'0'; //i可以理解为层数,第0层只有第一个数字,而最后一层就是整个多项式的值 }
相关文章:
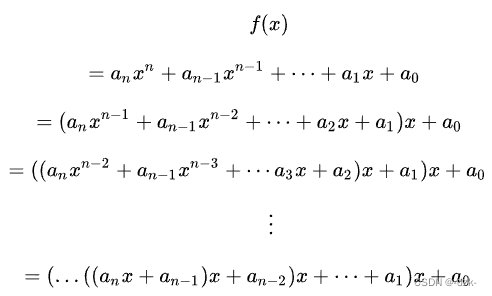
【蓝桥杯集训·每日一题】AcWing 2058. 笨拙的手指
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴哈希表秦九韶算法一、题目 1、原题链接 2058. 笨拙的手指 2、题目描述 奶牛贝茜正在学习如何在不同进制之间转换数字。 但是她总是犯错误,因为她无法轻易的用两…...

运维排查篇 | Linux 连接跟踪表满了怎么处理
nf_conntrack (在老版本的 Linux 内核中叫 ip_conntrack )是一个内核模块,用于跟踪一个网络连接的状态 一旦内核 netfilter 模块 conntrack 相关参数配置不合理,导致 nf_conntrack table full ,就会出现丢包、连接无法建立的问题 这个问题其…...
docker网络基
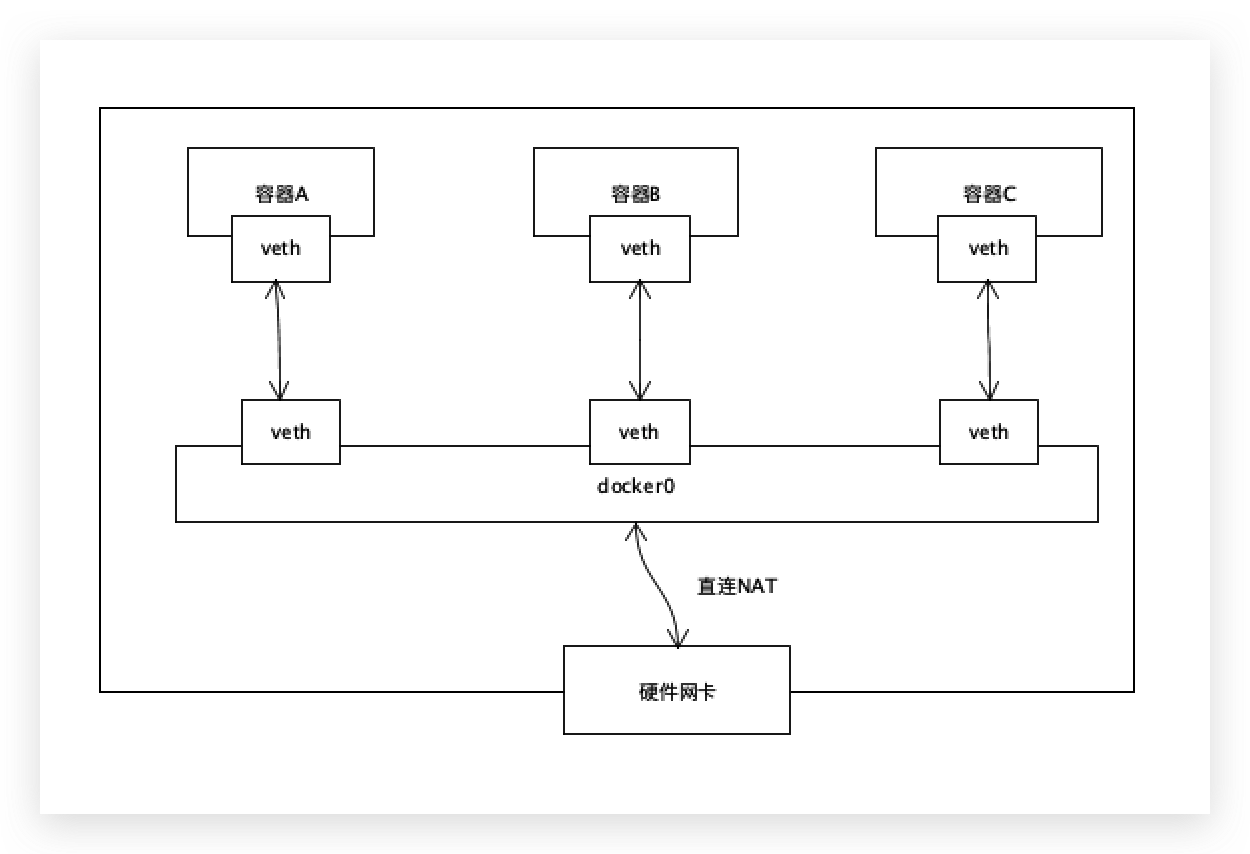
本文简单介绍下,容器之间的网络访问、容器与宿主机之间的网络访问、宿主机上有哪些网络接口。lolocal的简写,本地回环地址,127.0.0.1,它代表本地虚拟设备接口,默认被看作是永远不会宕掉的接口eth0ethernet的简写&#…...

C++:谈谈单例模式的多种实现形式
文章目录实现 1:静态成员实现 2:atexit 懒汉模式实现 3:原子变量 懒汉模式实现4:atexit 饿汉模式* 实现5:magic static单例模式:保证一个类仅有一个实例,并提供一个该实例的全局访问点。 稳…...
【Spring Cloud Alibaba】007-Nacos 配置*
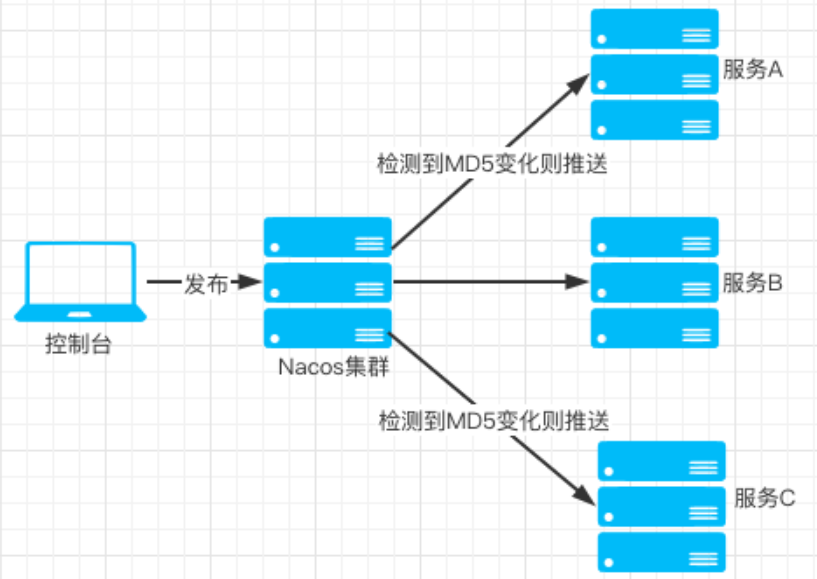
【Spring Cloud Alibaba】007-Nacos 配置* 文章目录【Spring Cloud Alibaba】007-Nacos 配置*一、概述1、概述2、对比 spring cloud config二、基本使用1、在管理界面新建配置2、启动权限3、 搭建 nacos-config 服务第一步:引入依赖第二步:修改 yaml 配置…...
《安富莱嵌入式周报》第304期:开源硬件耳机设计,AI单片机STM32N6已确定为M55内核,另外还有新品STM32H5, H50X, H7R, H7S发布
往期周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 更新一期视频教程: 第6期ThreadX视频教程:图文并茂吃透RTOS运行机制,任务管理&…...

vuex篇
1.简介(1)vuexVuex 是一个专为 Vue.js 应用程序开发的状态管理模式 库vuex是为vue.js开发的状态管理模式、组件状态集中管理(2)单页面数据流状态发生变化, 视图就重新渲染state发生变化时, 导致view视图发生改变, 视图通过操作action行为, 又会使得state状态发生变化(3)使用场…...

嵌入式开发:在嵌入式应用程序中混合C和C++
许多嵌入式应用程序仍使用c语言编写,但越来越多的嵌入式开发人员现在使用C语言编写程序。某些应用程序甚至共享这两种语言。这有意义吗?C是嵌入式应用中最常用的编程语言。多年来,人们一直期待着向C过渡,但过渡速度相当缓慢。但是࿰…...
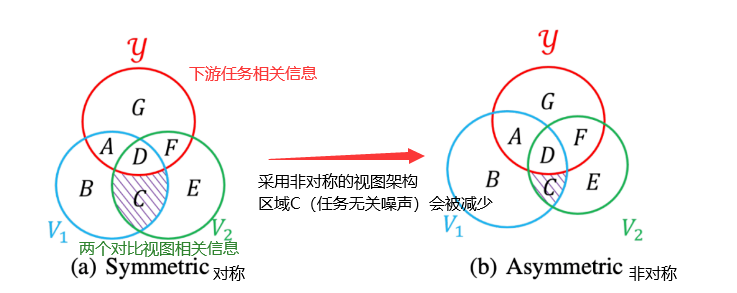
【2023/图对比/增强】MA-GCL: Model Augmentation Tricks for Graph Contrastive Learning
如果觉得我的分享有一定帮助,欢迎关注我的微信公众号 “码农的科研笔记”,了解更多我的算法和代码学习总结记录。或者点击链接扫码关注【2023/图对比/增强】MA-GCL: Model Augmentation Tricks for Graph Contrastive Learning 【2023/图对比/增强】MA-…...
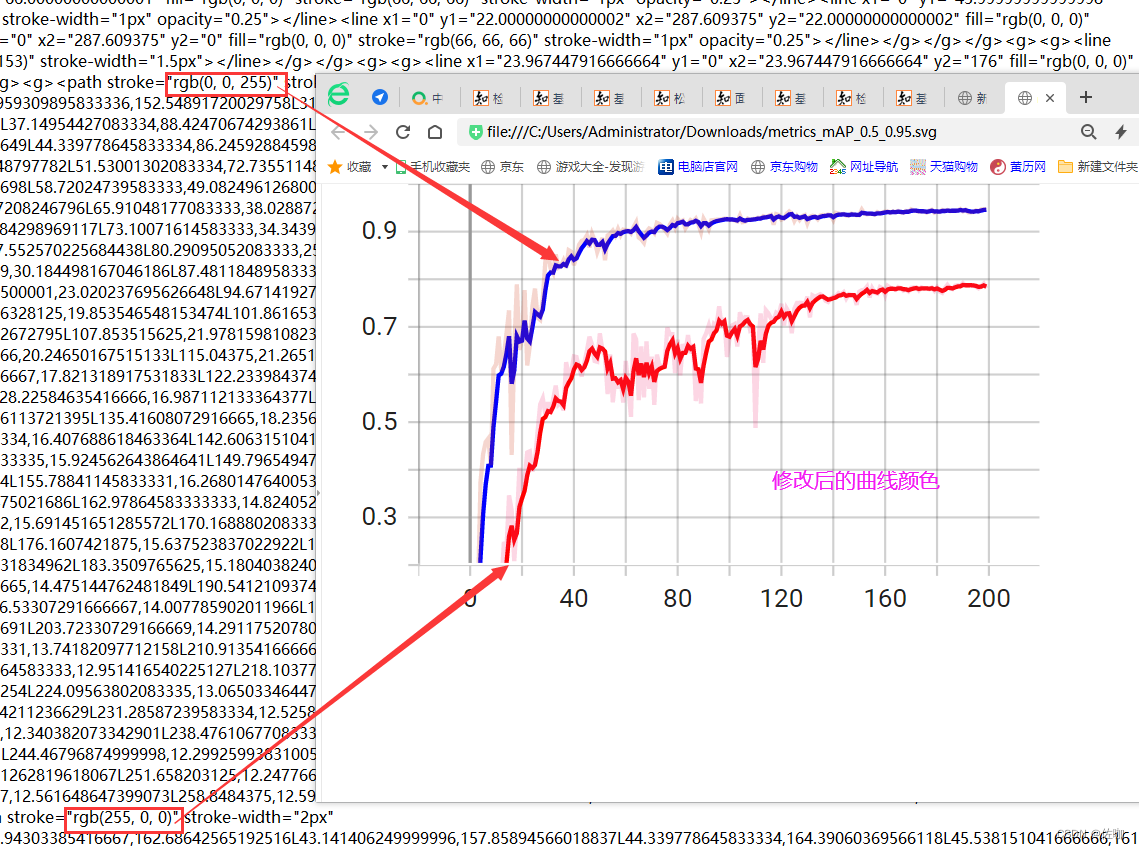
TensorBoard自定义修改单条及多条曲线颜色
在深度学习可视化训练过程中,曲线颜色是随机的,想要将好看的曲线颜色图放到论文中,就得自定义曲线颜色,具体方法见下文。 目录一、下载svg文件二、修改svg文件三、修改后曲线颜色对比四、总结一、下载svg文件 在TensorBoard界面中…...
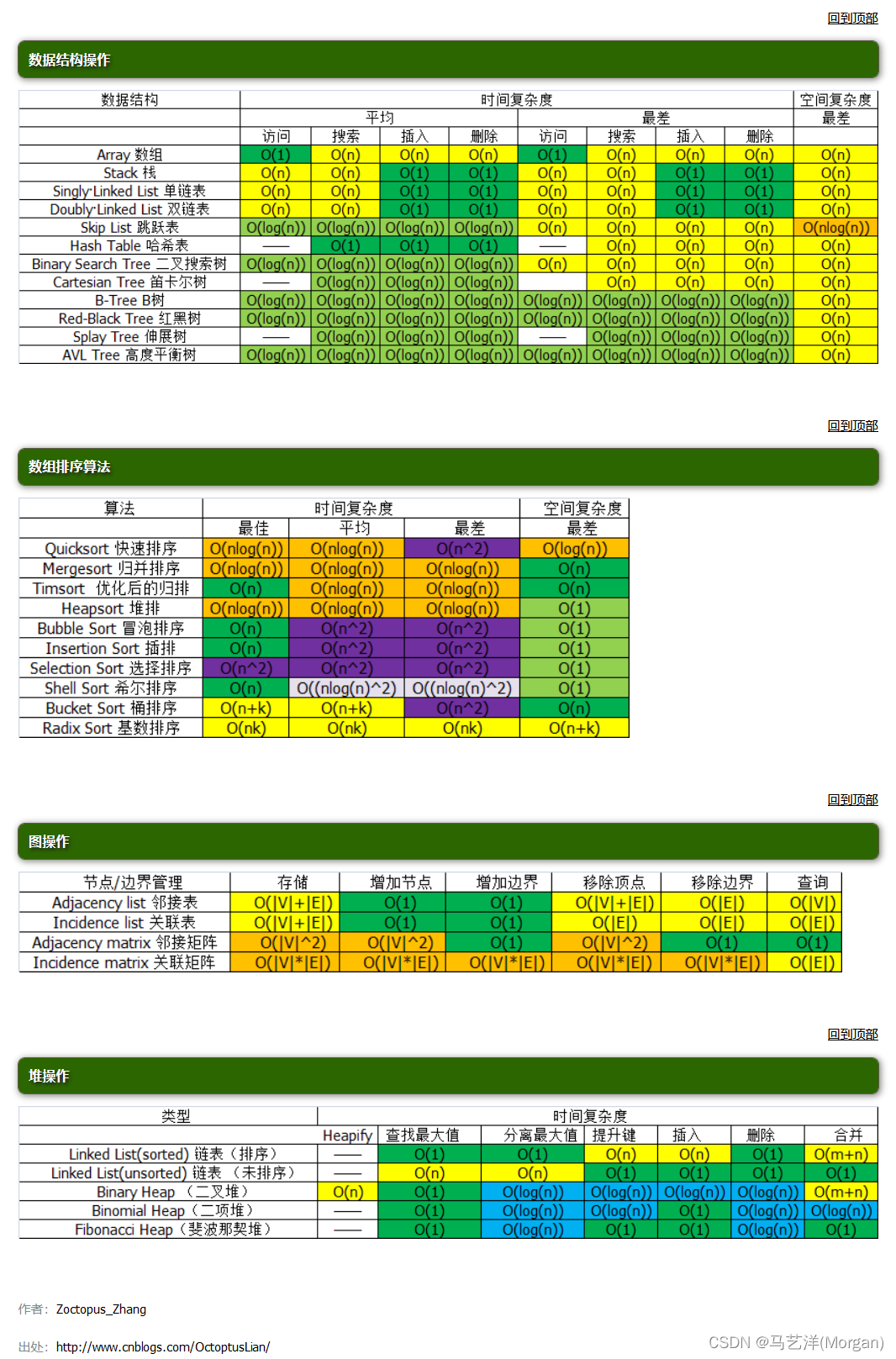
时间和空间复杂度
文章目录 前言 一、算法效率 1.如何评判算法效率? 2.算法的复杂度 二、时间复杂度 1.时间复杂度的定义 2. 大O的渐进表示法 三、空间复杂度 总结 前言 本文章讲解时间与空间复杂度 提示:以下是本篇文章正文内容,下面案例可供参考 一、算法…...

关于Linux下调试
关于Linux下调试 无论是内核(操作系统)还是应用程序,都存在需要调试的情况。 所谓工欲善其事,必先利其器。一个好的称手的工具,对于快速分析问题、定位问题,提高效率,非常有帮助。 除了工具&a…...

理解TP、FP、TN、FN
概念定义 按照常用的术语,将两个类分别称为正类 (positive) 和 负类 (negative)。使用数学表示: 1表示正类 , -1 表示负类。 正类通常是少数类,即样本较少的类(例如有缺陷的零件) 负类通常是多数类&#x…...
软考中级有用吗
当然有用了! 软考“简历”:计算机软件资格考试在全国范围内已经实施了二十多年,近十年来,考试规模持续增长,截止目前,累计报考人数约有五百万人。该考试由于其权威性和严肃性,得到了社会各界及用人单位的广泛认同&…...

计算机网络之IP协议(详解
网络层主管地址管理与路由选择。而IP协议就是网络层中一个非常重要的协议。它的作用就是在复杂的网络环境中确定一个合适的路径。IP协议头格式4位版本号(version) 指定IP协议的版本,目前只有两个版本:IP v4和IP v6.对于IP v4来说,这个值就是4…...

Kubernetes之探针probe
deployment只保证pod的状态为running。如果pod状态是running,但是里面丢失了文件,导致用户不能访问数据,则deployment是不管用的,此时就需要probe来检测pod是否正常工作。 probe是定义在容器里的,可以理解为容器里加的…...
高性能低功耗4口高速USB2.0 HUB NS1.1S 兼容FE1.1
NS1.1S是一款高性能、低功耗4口高速 USB2.0 HUB 控制器,上行端口兼容高速 480MHz和全速12MHz两种模式,4个下行端口兼容高速480MHz、全速12MHz、低速1.5MHz三种模式。 NS1.1S采用状态机单事务处理架构,而非单片机架构,多个事务缓冲…...

通过VS Code轻松连接树莓派
如果您正在使用树莓派作为开发平台,那么通过远程连接VS Code到树莓派是非常方便的一种方法。这样,您可以在Windows或macOS等计算机上开发和测试代码,而不必在树莓派上进行。 以下是通过VS Code远程连接到树莓派的步骤: 1.安装Re…...

图纸等敏感文件数据外发时 如何确保效率和安全性?
很多企业随着业务的发展,需要频繁的与外部供应商、合作伙伴之间进行数据的交换和使用。尤其是制造型企业,可能每天都要与几十、上百家供应商及合作伙伴进行产品数据交换。目前,大多数企业已经在内部实施了PDM/PLM系统,实现了对组织…...
)
2023年CDGA考试-第4章-数据架构(含答案)
2023年CDGA考试-第4章-数据架构(含答案) 单选题 1.请从下列选项中选择不属于数据架构师职责的选项 A.确保数据架构和企业战略及业务架构一致 B.提供数据和组件的标准业务词汇 C.设计企业数据模型 D.整合企业数据架构蓝图 答案 C 2.请从下列选项中选择不属于企业数据架构…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...