D1.Chopping Carrots (Easy Version)【数学,二分,暴力,思维】
链接
理论基础
已知正整数a,v,求证m=⌊av⌋是满足⌊am⌋⩾v的最大的m,其中x是正整数已知正整数a,v,求证m=\lfloor \frac {a}{v} \rfloor是满足\lfloor \frac {a}{m} \rfloor \geqslant v的最大的m,其中x是正整数已知正整数a,v,求证m=⌊va⌋是满足⌊ma⌋⩾v的最大的m,其中x是正整数
先证不等号成立根据整除的定义可以得到先证不等号成立根据整除的定义可以得到先证不等号成立根据整除的定义可以得到
a=vm+r(0⩽r<v)a=vm+r(0\leqslant r<v)a=vm+r(0⩽r<v)
⌊av⌋=m\lfloor \frac {a}{v} \rfloor=m⌊va⌋=m
⌊am⌋=⌊vm+rm⌋=v+⌊rm⌋⩾v\lfloor \frac {a}{m} \rfloor=\lfloor \frac {vm+r}{m} \rfloor=v+\lfloor \frac {r}{m} \rfloor \geqslant v⌊ma⌋=⌊mvm+r⌋=v+⌊mr⌋⩾v
再证这个m是满足不等式的最大的m,是m的极限值,用反证法再证这个m是满足不等式的最大的m,是m的极限值,用反证法再证这个m是满足不等式的最大的m,是m的极限值,用反证法
如果存在这样的数使得不等式成立,只需证m+1使得这样的不等式成立如果存在这样的数使得不等式成立,只需证m+1使得这样的不等式成立如果存在这样的数使得不等式成立,只需证m+1使得这样的不等式成立
⌊am+1⌋=⌊vm+rm+1⌋=⌊v(m+1)+r−vm+1⌋=v+⌊r−vm+1⌋\lfloor \frac {a}{m+1} \rfloor=\lfloor \frac {vm+r}{m+1} \rfloor=\lfloor \frac {v(m+1)+r-v}{m+1} \rfloor=v+\lfloor \frac {r-v}{m+1} \rfloor⌊m+1a⌋=⌊m+1vm+r⌋=⌊m+1v(m+1)+r−v⌋=v+⌊m+1r−v⌋
其中r−v是负数,根据高斯函数的定义,⌊r−vm+1⌋⩽−1其中r-v是负数,根据高斯函数的定义,\lfloor \frac {r-v}{m+1} \rfloor \leqslant-1其中r−v是负数,根据高斯函数的定义,⌊m+1r−v⌋⩽−1
∴⌊am+1⌋<v\therefore \lfloor \frac {a}{m+1} \rfloor <v∴⌊m+1a⌋<v
故不存在更大的m了故不存在更大的m了故不存在更大的m了
分析
这道题,由于数值比较小,我们考虑枚举下限0~a[0],虽然有些数值不一定取到但是没有关系,因为,如果真的没有任何一个数能够取到的话,只要改变数值的大小就可以使得某一个数取到,这样差值就会变小,刚刚的非法的答案就不会有影响。对于某个下限,我们枚举最大的p使得不等式成立,也就是让整除结果尽可能接近v使得差值最小。因为差值最小是零,所有我们可以枚举所有的下限,尽管可能有些数是取不到的但是这些下限必然是不少最终的 答案,所有没有关系。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (p << 1)
#define rs (p << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 3005;
int a[N];
void solve() {int n, k;cin >> n >> k;for (int i = 1; i <= n; i++) cin >> a[i];int ans = inf;for (int i = 0; i <= a[1]; i++) {int maxn = 0;for (int j = 1; j <= n; j++) {int x = min(k, (i ? (a[j] / i) : k));//居然不考虑零也是可以的,我也是很迷惑的,如果真的想不到这个东西其实也是可以用二分的maxn = max(maxn, a[j] / x);}ans = min(ans, maxn - i);}cout << ans << '\n';
}
int main(){ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) solve();return 0;
}
相关文章:
【数学,二分,暴力,思维】)
D1.Chopping Carrots (Easy Version)【数学,二分,暴力,思维】
链接 理论基础 已知正整数a,v,求证m⌊av⌋是满足⌊am⌋⩾v的最大的m,其中x是正整数已知正整数a,v,求证m\lfloor \frac {a}{v} \rfloor是满足\lfloor \frac {a}{m} \rfloor \geqslant v的最大的m,其中x是正整数已知正整数a,v,求证m⌊va⌋是满足⌊ma⌋…...

【Maven】(二)使用 Maven 创建并运行项目、聊聊 POM 中的坐标与版本号的规则
文章目录1.前言2.hello-world2.1.Archetype 创建2.2.使用 IDE 创建2.3.Maven的目录结构3.pom的基本组成3.1.Maven坐标的概念与规则3.2.版本号规则2.3.打包成可运行的JAR4.结语1.前言 本系列文章记录了从0开始到实战系统了解 Maven 的过程,Maven 系列历史文章&#…...
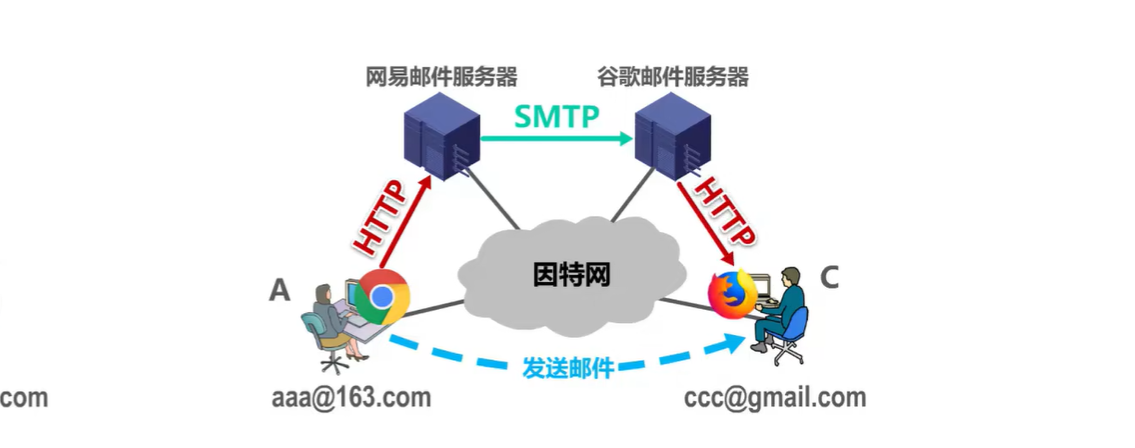
(考研湖科大教书匠计算机网络)第六章应用层-第六节:电子邮件
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:电子邮件(1)概述(2)举例二:简单邮件传送协议SMTP(1)SMTP基本工作…...

一、初识TypeScript、什么是类型系统
初识TypeScript、什么是类型系统 快速上手TypeScript 安装方式: > npm install -g typescriptTypeScript是JavaScript类型的超集,包含JS的所有语法,它可以编译成纯JavaScript。 意味着,纯js代码可以在.ts后缀名文件中编译 …...
)
一文了解什么是字节对齐(超详细)
什么是字节对齐 1.空类 class A {}对空类做sizeof()计算时应当等于1 2.带虚函数的类 如果有一个类,包含两个32位整型的数据成员,一个普通成员函数,还有一个virtual虚函数,在32位机器上,这个…...
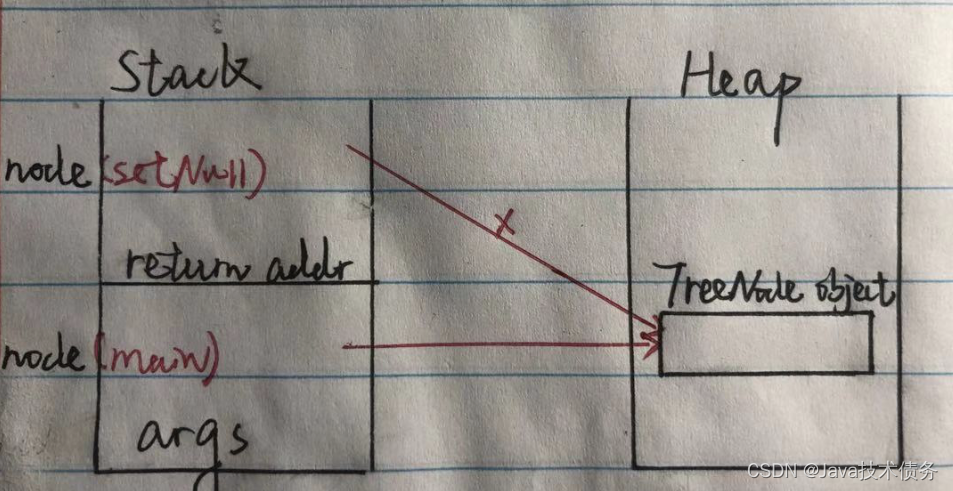
Java无法通过形参设置为null改变实参
文章目录问题描述问题例子问题分析问题描述 在实际业务开发过程中,我们会把实参传递给形参,在方法体内对引用对象进行构建或者修改,从而改变实参,因为对形参对象属性修改时,实参对象也会随着改变,详情请看&…...

GEE:样本点选择教程
本文记录了在GEE平台上标记样本的技巧和代码脚本,样本点可以用来做土地利用分类、植被提取、水藻提取、冰川提取、农作物提取等应用中。可以应用到的方法包括随机森林(RF)分类,支持矢量机(SVM)分类…...

3.知识图谱相关学习资料汇总,提供系统化的知识图谱学习路径。一份详细的指南,补全你知识的漏洞
目录 理论及论文图谱及数据集工具及服务白皮书及报告机构及人物视频课程专栏合集评测竞赛项目案例推广技术文章1. 整体概念架构 随着知识图谱的发展,与之相关的概念也越来越多,在阅读论文时先准确的把握该论文所要解决问题处于的层级或者位置对于更好的理解论文也比较有帮助…...
TypeScript学习笔记(一)编译环境、数据类型、函数类型、联合类型
文章目录编译环境基本类型函数类型函数重载联合类型和函数重载编译环境 TypeScript最终会被编译成JavaScript来运行,所以我们需要搭建对应的环境。 首先我们要全局安装typescript # 安装命令 npm install typescript -g # 查看版本 tsc --version⭐️ 方式一&…...

为什么要移除数据库物理外键?
在最早接触数据库的时候,会接触数据库三范式,在表和表之间有关系的时候,需要使用外键添加约束 外键的好处: 1、由数据库自身保证数据一致性,完整性,更可靠,因为程序很难100%保证数据…...

Linux 计划任务讲解
目录 计划任务 一次性计划任务 长期性计划任务 计划任务 管理员可以编辑自己的和普通用户的计划任务 普通用户只可以编辑自己的计划任务 计划任务根据执行方式分为一次性计划任务、长期性计划任务 一次性计划任务 此计划只执行一次,执行后或就不会再执行了 通…...

Qt智能指针模板类的使用方式和区别总结
问题描述: 前面有篇文章,写了我建议在函数中new一个指针的时候最好使用QPointer模板类,这样就可以不用后面再加detele pointer的清除操作。当时觉得用QPointer的原因主要是QScopedPointer和QSharedPointer这两个类写起来太长了,费劲。所以觉得QPointer挺好的。 不过,看到…...
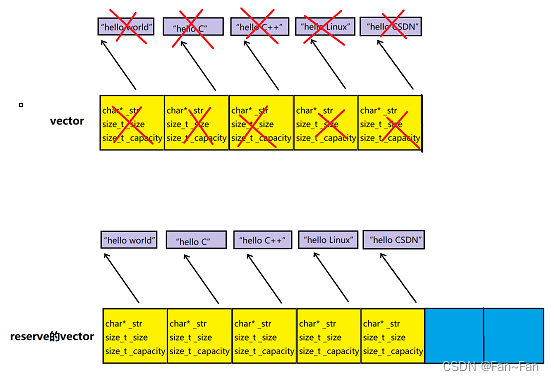
【STL】模拟实现vector
目录 1、基本成员变量 2、默认成员函数 构造函数 析构函数 拷贝构造函数 赋值运算符重载函数 3、容器访问相关函数接口 operator [ ]运算符重载 迭代器 范围for 4、vector容量和大小相关函数 size和capacity reserve扩容 resize swap交换数据 empty 5、修…...
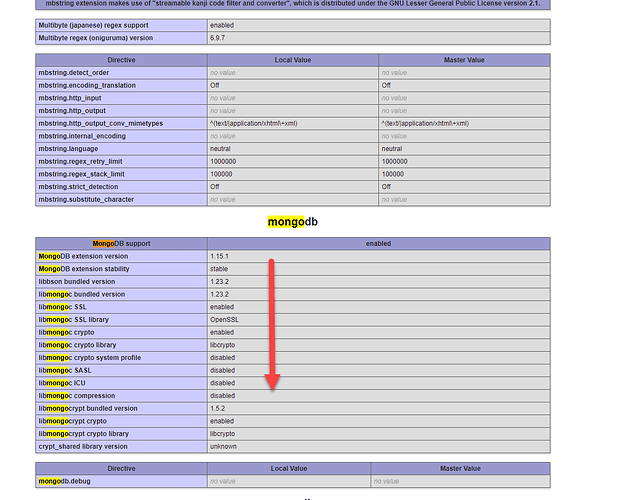
Window 的 PHP XAMPP 安装 mongodb 的扩展
需要安装的扩展为:extensionphp_mongodb.dll根据官方的指引:PHP: Installing the MongoDB PHP Driver on Windows - Manual 1需要到 GitHub 上下载扩展,然后进行安装。这里的版本选择有些讲究。首先1.51 是 mongoDB 的驱动版本号,…...

Codeforces Round #849 (Div. 4)(E~G)
A~D比较简单就不写了,哎嘿E. Negatives and Positives给出一个数组a,可以对数组进行若干次操作,每次操作可以将相邻的两个数换为它们的相反数,求进行若干次操作之后能得到数组和的最大值是多少。思路:最大的肯定是把负…...

网易云音乐财报解读:收入大增亏损收窄,“云村”草长莺飞
独家版权时代结束后,在线音乐产业进入了新的发展阶段,各家音乐平台经营状况备受关注。 2月23日,网易云音乐公布了2022年全年财务业绩。财报显示,网易云音乐2022年全年收入为90亿元,较2021年同比增长28.5%。 值得一提的…...

MariaDB-10.8.6安装+主从搭建
【系统版本】CentOS 7.x Linux version 3.10.0-1062.18.1.el7.x86_64【检查系统是否安装过Mysql|mariadb】【查看是否安装Mysql|mariadb】#搜索mysql rpm -qa|grep mysql #搜索mariadb rpm -qa|grep mariadb #搜索MariaDB rpm -qa|grep MariaDB #如果安装过Mysql|mariadb&#…...
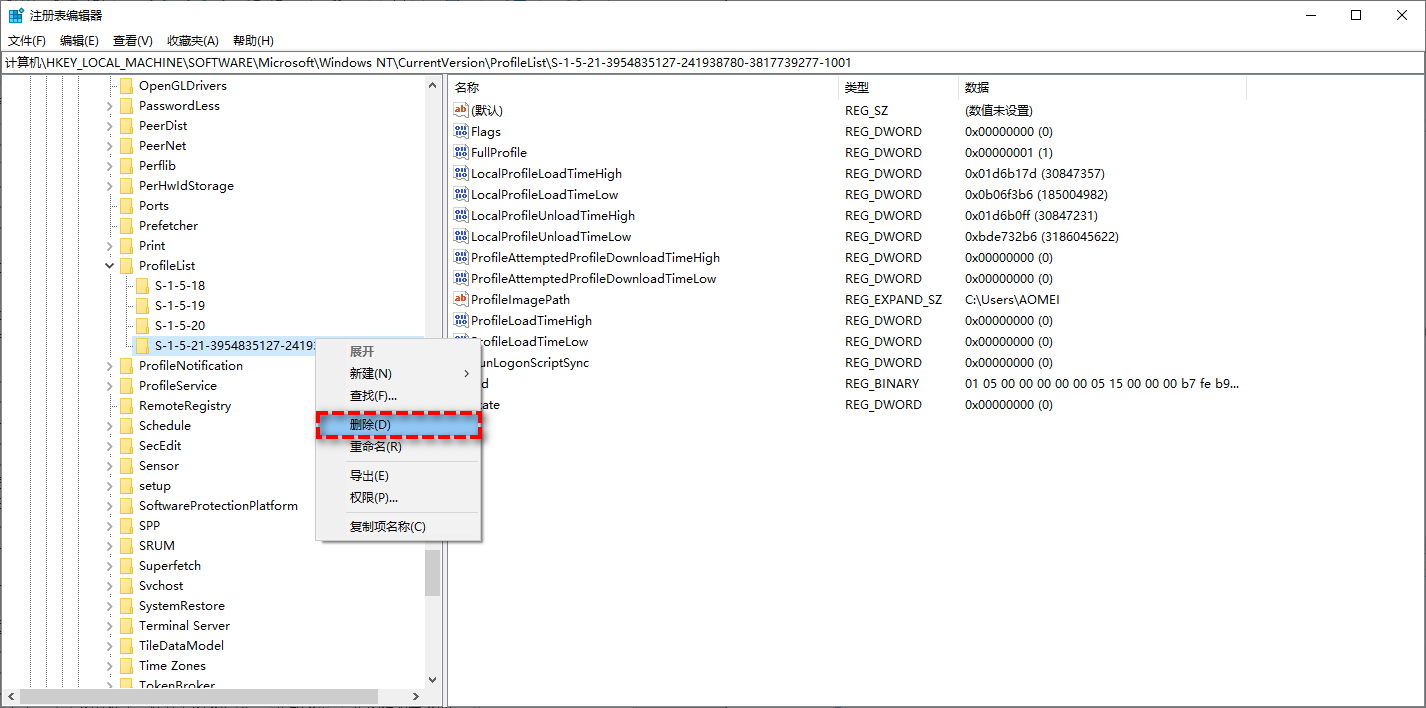
Win11系统user profile service服务登录失败解决方法
Win11系统user profile service服务登录失败解决方法分享。有用户在使用电脑的时候遇到了一些问题,系统的user profile service服务无法登录了。出现这个问题可能是系统文件损坏,或者中了病毒。接下来我们一起来看看如何解决这个问题的操作方法分享吧。 …...
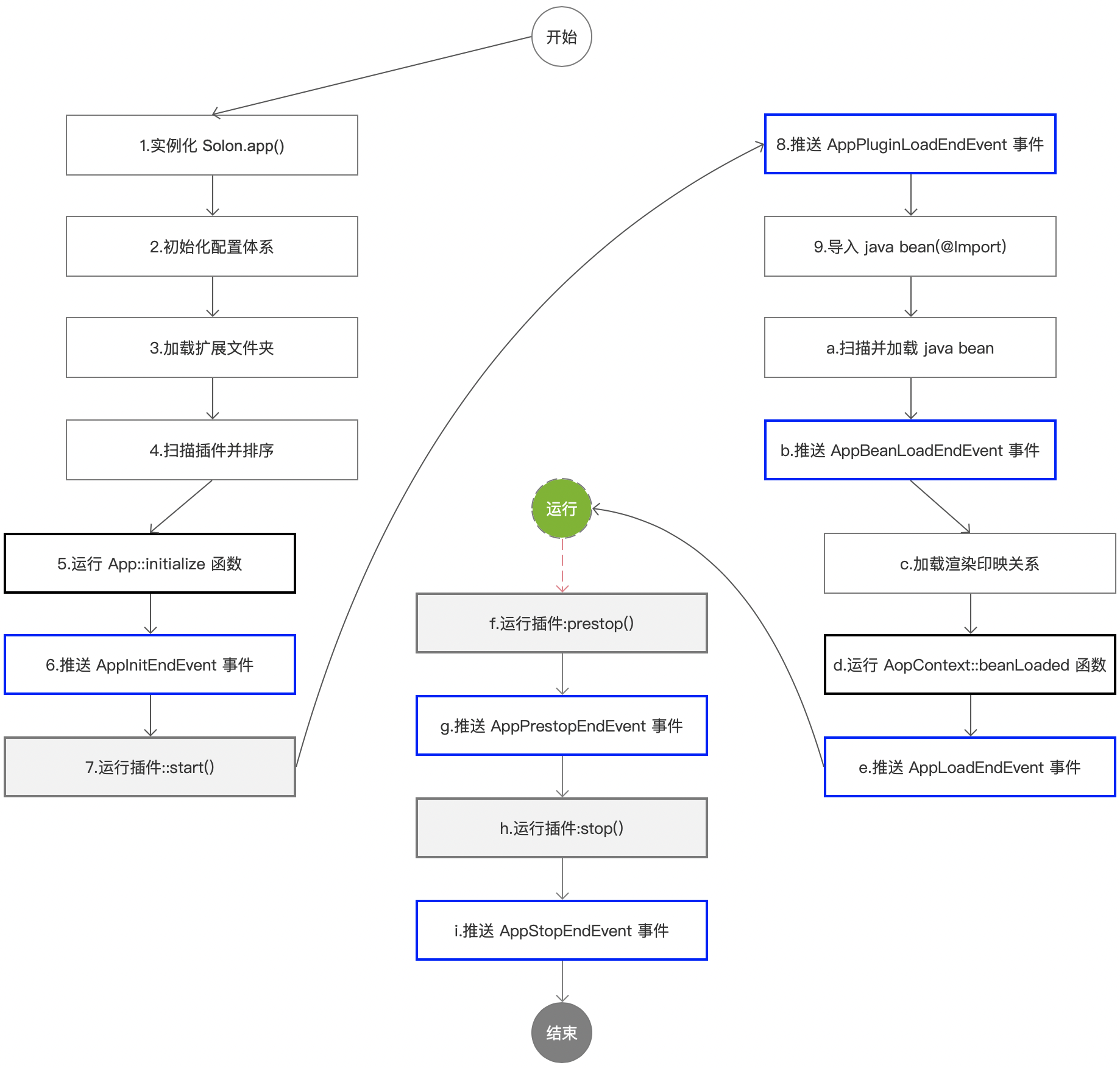
Solon2 之基础:四、应用启动过程与完整生命周期
串行的处理过程(含六个事件扩展点 两个函数扩展点),代码直接、没有什么模式。易明 提醒: 启动过程完成后,项目才能正常运行(启动过程中,不能把线程卡死了)AppBeanLoadEndEvent 之前…...
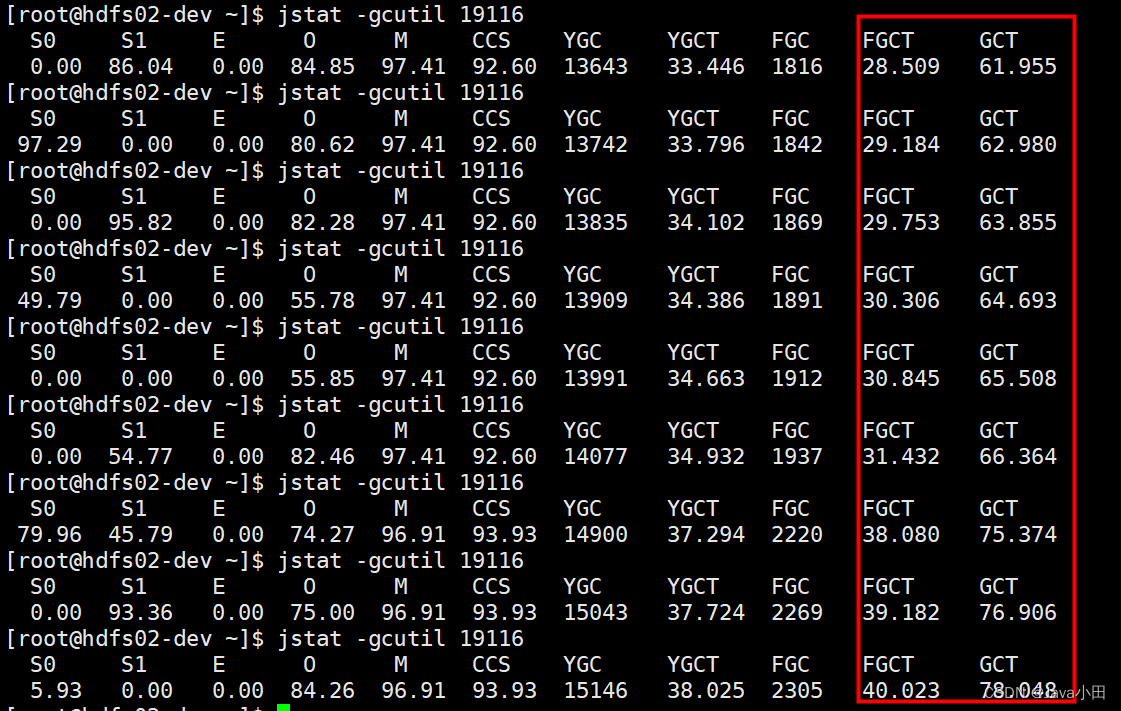
Java性能分析
0、问题代码: 代码问题其实很明显,但是这里主要是为了练习如何使用工具进行分析 所以最好先不要看代码,假装不知道程序逻辑,而是先通过工具去分析,再结合分析数据去看代码,从而推出问题点在哪 import jav…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
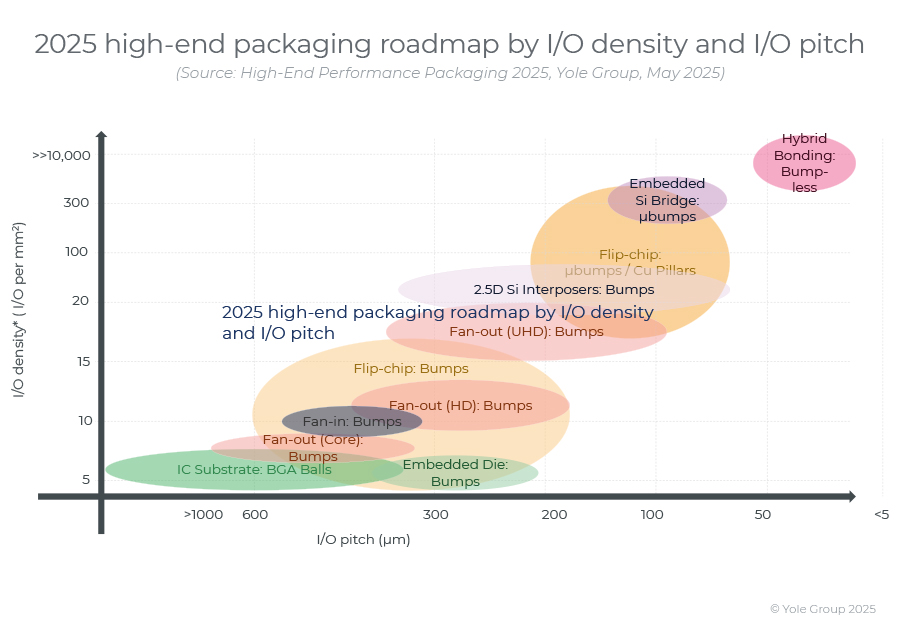
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
