幂级数和幂级数的和函数有什么关系?
幂级数和幂级数的和函数有什么关系?
本文例子引用自:80_1幂级数运算,逐项积分、求导【小元老师】高等数学,考研数学
求幂级数 ∑ n = 1 ∞ 1 n x n \sum\limits_{n=1}^{\infty}\frac{1}{n}x^n n=1∑∞n1xn 的和函数
(1)求收敛半径,由于是不缺项级数所以可以使用 lim n → ∞ ∣ a n + 1 a n ∣ = ρ \lim\limits_{n\rightarrow\infty}|\frac{a_{n+1}}{a_n}|=\rho n→∞lim∣anan+1∣=ρ,若是缺项级数则只能使用 lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ = ρ ∣ ϕ ( x ) ∣ < 1 \lim\limits_{n\rightarrow\infty}|\frac{u_{n+1}(x)}{u_n(x)}|=\rho|\phi(x)|\lt 1 n→∞lim∣un(x)un+1(x)∣=ρ∣ϕ(x)∣<1,当然不缺项级数也可使用后者。
ρ = lim n → ∞ ∣ a n + 1 a n ∣ = lim n → ∞ ∣ 1 n + 1 1 n ∣ = 1 \rho=\lim\limits_{n\rightarrow\infty}|\frac{a_{n+1}}{a_n}|=\lim\limits_{n\rightarrow\infty}|\frac{\frac{1}{n+1}}{\frac{1}{n}}|=1 ρ=n→∞lim∣anan+1∣=n→∞lim∣n1n+11∣=1
(2)判断端点处的敛散性
当 x = − 1 x=-1 x=−1 时, ∑ n = 1 ∞ ( − 1 ) n 1 n \sum\limits_{n=1}^{\infty}(-1)^n\frac{1}{n} n=1∑∞(−1)nn1, u n = 1 n → 0 u_n=\frac{1}{n}\rightarrow0 un=n1→0 且 u n = 1 n u_n=\frac{1}{n} un=n1递减,级数收敛(利用交错级数的莱布尼茨定理判别)
当 x = 1 x=1 x=1 时, ∑ n = 1 ∞ 1 n \sum\limits_{n=1}^{\infty}\frac{1}{n} n=1∑∞n1, p = 1 p=1 p=1,级数发散(利用p级数判别)
(3)综上,该级数收敛域 [ − 1 , 1 ) [-1,1) [−1,1)
(4)求收敛域中幂级数的和函数(在收敛域中幂级数等于其和函数,超过收敛域二者不等)
s ( x ) = ∑ n = 1 ∞ 1 n x n = x + 1 2 x 2 + 1 3 x 3 + ⋯ + 1 n x n + ⋯ s(x)=\sum\limits_{n=1}^{\infty}\frac{1}{n}x^n=x+\frac{1}{2}x^2+\frac{1}{3}x^3+\cdots+\frac{1}{n}x^n+\cdots s(x)=n=1∑∞n1xn=x+21x2+31x3+⋯+n1xn+⋯
逐项求导
s ′ ( x ) = ( ∑ n = 1 ∞ 1 n x n ) ′ = 1 + x + x 2 + ⋯ + 1 n x n − 1 + ⋯ = 1 1 − x s'(x)=\big(\sum\limits_{n=1}^{\infty}\frac{1}{n}x^n\big)'=1+x+x^2+\cdots+\frac{1}{n}x^{n-1}+\cdots=\frac{1}{1-x} s′(x)=(n=1∑∞n1xn)′=1+x+x2+⋯+n1xn−1+⋯=1−x1
左右两端同时积分(右侧逐项积分)
s ( x ) = s ( 0 ) + ∫ 0 x s ′ ( t ) d t = 0 + ∫ 0 x 1 1 − t d t = − ln ( 1 − x ) s(x)=s(0)+\int_0^xs'(t)dt=0+\int_0^x\frac{1}{1-t}dt=-\ln(1-x) s(x)=s(0)+∫0xs′(t)dt=0+∫0x1−t1dt=−ln(1−x)
上式为什么还有 s ( 0 ) s(0) s(0)?
∫ 0 x s ′ ( t ) d t = s ( x ) ∣ 0 x = s ( x ) − s ( 0 ) s ( x ) = s ( 0 ) + ∫ 0 x s ′ ( t ) d t \int_0^xs'(t)dt=s(x)|_0^x=s(x)-s(0)\\ ~\\ s(x)=s(0)+\int_0^xs'(t)dt ∫0xs′(t)dt=s(x)∣0x=s(x)−s(0) s(x)=s(0)+∫0xs′(t)dt
最终收敛域上幂级数的和函数为:
s ( x ) = − ln ( 1 − x ) , x ∈ [ − 1 , 1 ) s(x)=-\ln(1-x),x\in[-1,1) s(x)=−ln(1−x),x∈[−1,1)
我们为什么要兜圈子先对级数求导(或积分)然后再进行积分(或求导)呢?
主要想利用等比级数,因为其和函数容易求得,而逐项求导和积分的目的是将所给幂级数变换为等比级数,随后利用等比级数求出所给幂级数的和函数

我们在图像中看看到底幂级数和幂级数的和函数有什么关系?
下图中幂级数的图像为绿色曲线,其实不是真正的图像,因为 n n n为无穷大,笔者这里 n n n只取到了9,仅做示意。下图中红色曲线为幂级数和函数的图像,我们可以发现在收敛域中幂级数等于其和函数,超过收敛域二者是不等的

相关文章:

幂级数和幂级数的和函数有什么关系?
幂级数和幂级数的和函数有什么关系? 本文例子引用自:80_1幂级数运算,逐项积分、求导【小元老师】高等数学,考研数学 求幂级数 ∑ n 1 ∞ 1 n x n \sum\limits_{n1}^{\infty}\frac{1}{n}x^n n1∑∞n1xn 的和函数 ÿ…...

Git多账号管理通过ssh 公钥的方式,git,gitlab,gitee
按照目前国内访问git,如果不科学上网,我们很大可能访问会超时。基于这个,所以我现在的git 配置已经增加到了3个了 一个公司gitlab,一个git,一个gitee. 以下基于这个环境,我们来说明下如何创建配置ssh公钥。…...

在nodejs常见的不良做法及其优化解决方案
在nodejs常见的不良做法及其优化解决方案 当涉及到在express和nodejs中开发应用程序时。遵循最佳实践对于确保项目的健壮性、可维护性和安全性至关重要。 在本文中,我们将探索开发人员经常遇到的几种常见的错误做法,并通过代码示例研究优化的最佳做法&…...

关于layui upload上传组件上传文件无反应的问题
最近使用layui upload组件时,碰到了上传文件无反应的问题,感到非常困惑。 因为使用layui upload组件不是一次两次了,之前每次都可以,这次使用同样的配方,同样的姿势,为什么就不行了呢? 照例先…...

容器网络之Flannel
第一个问题位置变化,往往是通过一个称为注册中心的地方统一管理的,这个是应用自己做的。当一个应用启动的时候,将自己所在环境的 IP 地址和端口,注册到注册中心指挥部,这样其他的应用请求它的时候,到指挥…...
:如何进行乳腺癌检测?)
SVM(下):如何进行乳腺癌检测?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

嵌入式Linux应用开发-第十五章具体单板的按键驱动程序
嵌入式Linux应用开发-第十五章具体单板的按键驱动程序 第十五章 具体单板的按键驱动程序(查询方式)15.1 GPIO操作回顾15.2 AM335X的按键驱动程序(查询方式)15.2.1 先看原理图确定引脚及操作方法15.2.2 再看芯片手册确定寄存器及操作方法15.2.3 编程15.2.3.1 程序框架15.2.3.2 硬…...
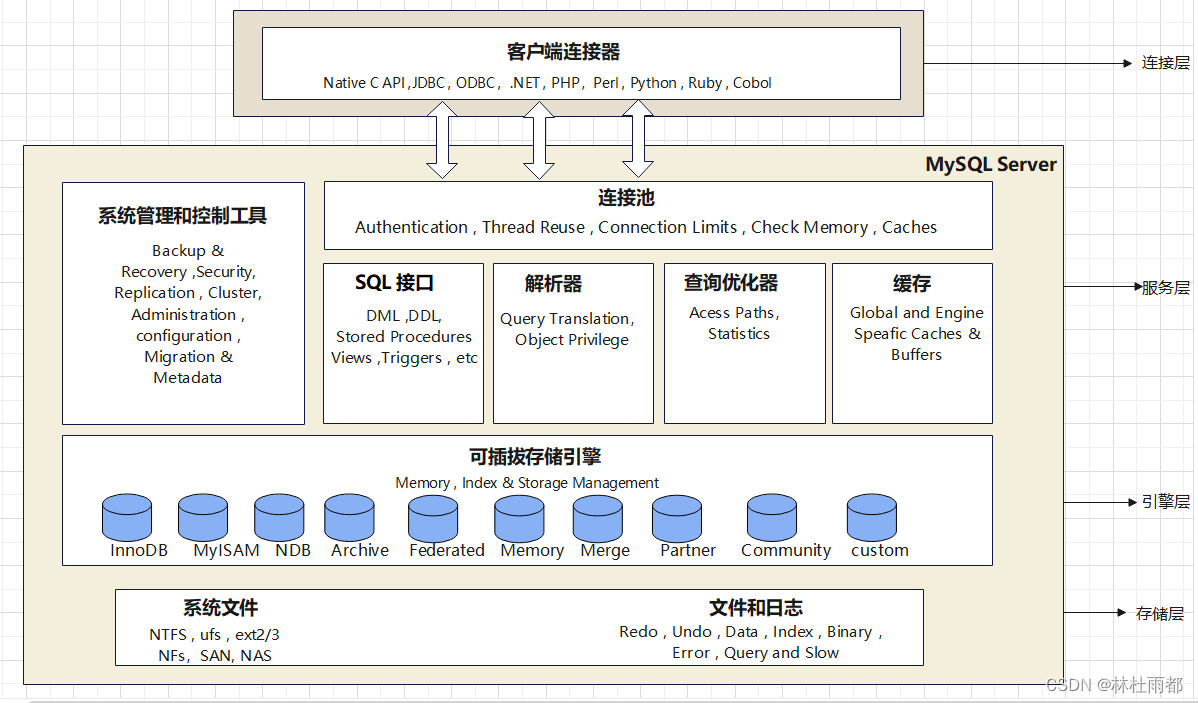
MySQL体系结构和四层架构介绍
MySQL体系结构图如下: 四层介绍 1. 连接层: 它的主要功能是处理客户端与MySQL服务器之间的连接(比如Java应用程序通过JDBC连接MySQL)。当客户端应用程序连接到MySQL服务器时,连接层对用户进行身份验证、建立安全连接并管理会话状态。它还处理…...

【产品运营】如何做好B端产品规划
产品规划是基于当下掌握的多维度信息,为追求特定目的,而制定的产品资源投入计划。 产品规划是基于当下掌握的多维度信息(客户需求、市场趋势、竞争对手、竞争策略等),为追求特定目的(商业增长、客户满意等&…...

ruoyi-启动
1 springboot 版本 git 地址 ruoyi-vue-pro: 🔥 官方推荐 🔥 RuoYi-Vue 全新 Pro 版本,优化重构所有功能。基于 Spring Boot MyBatis Plus Vue & Element 实现的后台管理系统 微信小程序,支持 RBAC 动态权限、数据权限…...
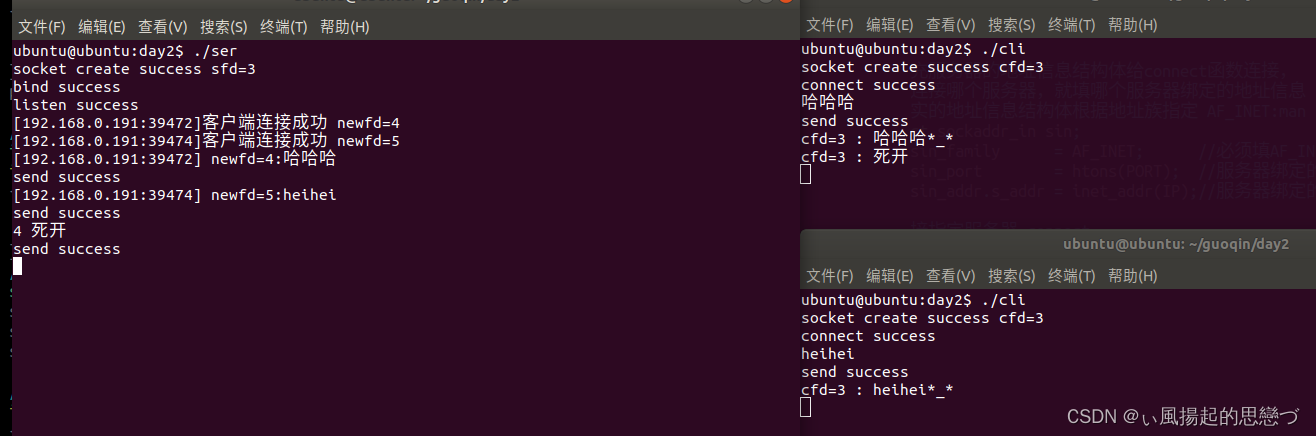
select完成服务器并发
服务器 #include <myhead.h>#define PORT 4399 //端口号 #define IP "192.168.0.191"//IP地址//键盘输入事件 int keybord_events(fd_set readfds); //客户端交互事件 int cliRcvSnd_events(int , struct sockaddr_in*, fd_set *, int *); //客户端连接事件 …...
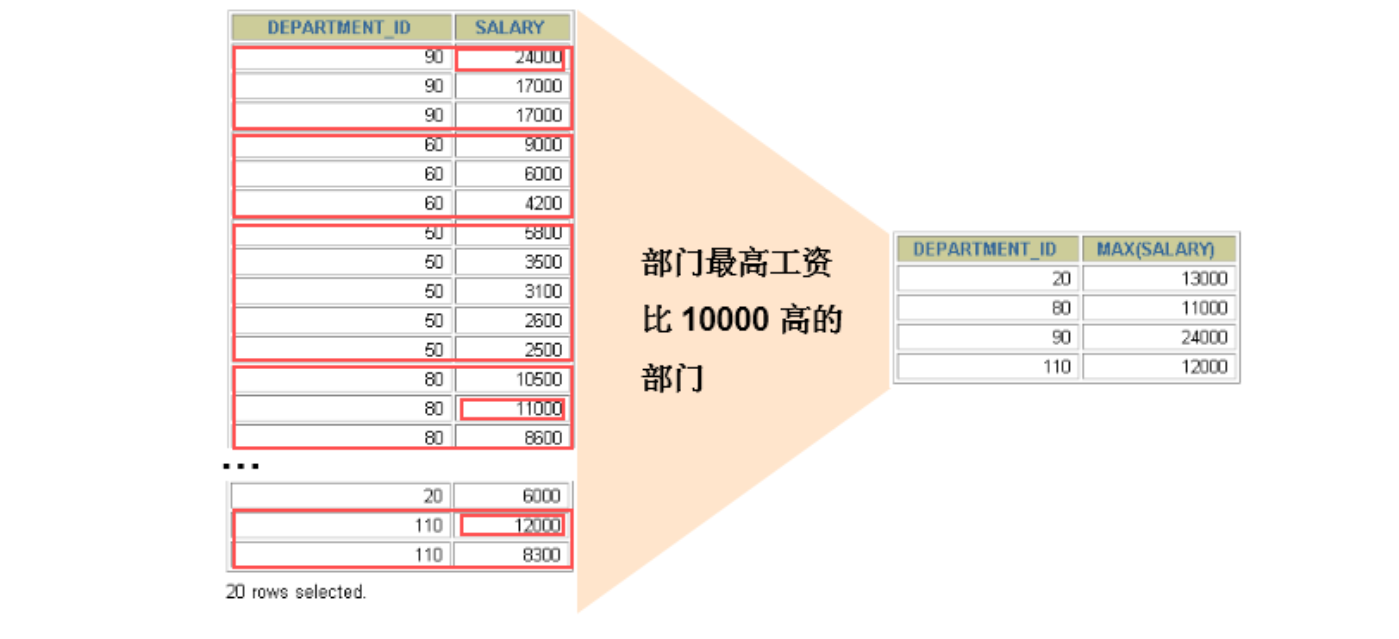
初级篇—第四章聚合函数
文章目录 聚合函数介绍聚合函数介绍COUNT函数AVG和SUM函数MIN和MAX函数 GROUP BY语法基本使用使用多个列分组WITH ROLLUP HAVING基本使用WHERE和HAVING的对比开发中的选择 SELECT的执行过程查询的结构SQL 的执行原理 练习流程函数 聚合函数介绍 聚合函数作用于一组数据&#x…...
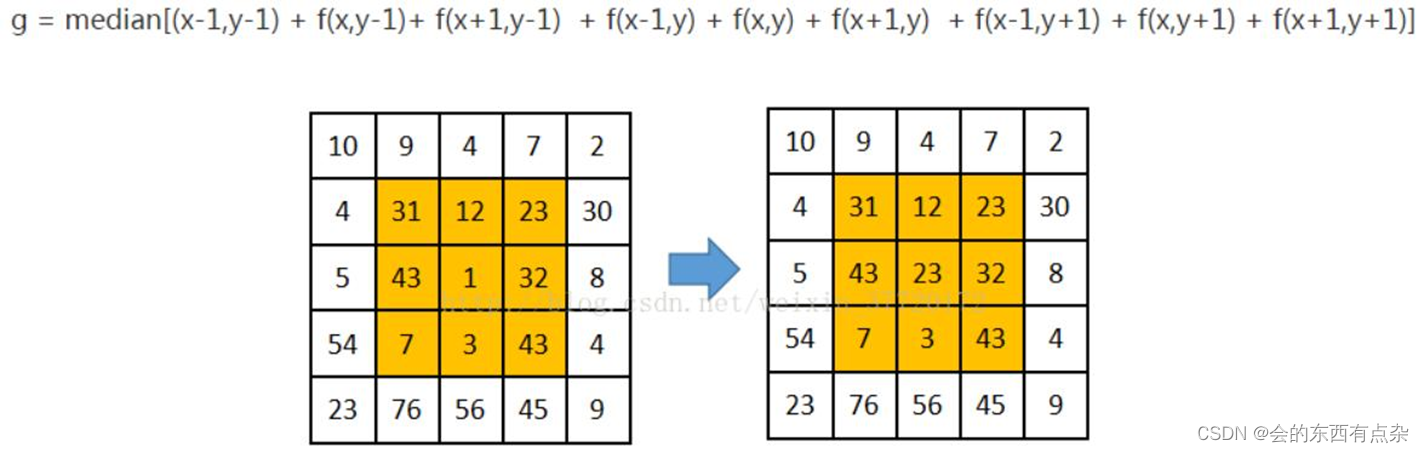
计算机图像处理-中值滤波
非线性滤波 非线性滤波是利用原始图像跟模版之间的一种逻辑关系得到结果,常用的非线性滤波方法有中值滤波和高斯双边滤波,分别对应cv2.medianBlur(src, ksize)方法和cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])方法。 …...

Golang中的包和模块设计
Go,也被称为Golang,是一种静态类型、编译型语言,因其简洁性和对并发编程的强大支持而受到开发者们的喜爱。Go编程的一个关键方面是其包和模块系统,它允许创建可重用、可维护和高效的代码。本博客文章将深入探讨在Go中设计包和模块…...
web:[极客大挑战 2019]Upload
题目 页面显示为一个上传,猜测上传一句话木马文件 先查看源代码看一下有没有有用的信息,说明要先上传图片,先尝试上传含有一句话木马的图片 构造payload <?php eval($_POST[123]);?> 上传后页面显示为,不能包含<&…...
ICMP差错包
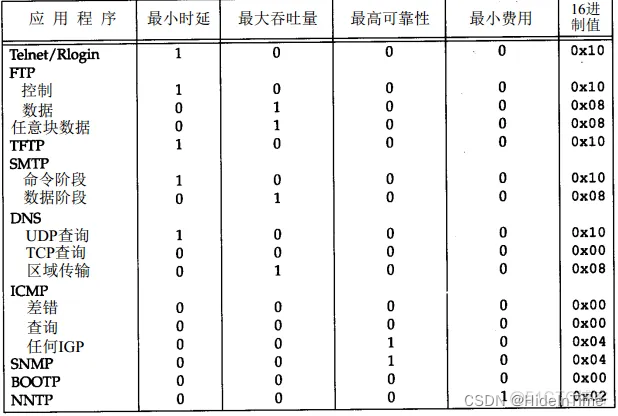
ICMP报文分类 Type Code 描述 查询/差错 0-Echo响应 0 Echo响应报文 查询 3-目的不可达 0 目标网络不可达报文 差错 1 目标主机不可达报文 差错 2 目标协议不可达报文 差错 3 目标端口不可达报文 差错 4 要求分段并设置DF flag标志报文 差错 5 源路由…...
算法基础课第二部分
算法基础课 第四讲 数学知识AcWing1381. 阶乘(同余,因式分解) 质数AcWing 866. 质数的判定---试除法AcWing 868. 质数的判定---埃氏筛AcWing867. 分解质因数---试除法AcWing 197. 阶乘---分解质因数---埃式筛 约数AcWing 869. 求约数---试除法AcWing 870. 约数个数-…...

【数据结构】外部排序、多路平衡归并与败者树、置换-选择排序(生成初始归并段)、最佳归并树算法
目录 1、外部排序 1.1 基本概念 1.2 方法 2、多路平衡归并与败者树 2.1 K路平衡归并 2.2 败者树 3、置换-选择排序(生成初始归并段)编辑 4、最佳归并树 4.1 理论基础编辑 4.2 构造方法 编辑 5、各种排序算法的性质 1、外部排序 1.1 基本概…...

抽象工厂模式 创建性模式之五
在看这篇文章之前,请先看看“简单工厂模式”和“工厂方法模式”这两篇博文,会更有助于理解。我们现在已经知道,简单工厂模式就是用一个简单工厂去创建多个产品,工厂方法模式是每一个具体的工厂只生产一个具体的产品,然…...

servlet如何获取PUT和DELETE请求的参数
1. servlet为何不能获取PUT和DELETE请求的参数 Servlet的规范是POST的数据需要转给request.getParameter*()方法,没有规定PUT和DELETE请求也这么做 The Servlet spec requires form data to be available for HTTP POST but not for HTTP PUT or PATCH requests. T…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
