【仔细理解】计算机视觉基础1——特征提取之Harris角点
Harris角点是图像特征提取中最基本的方法,本篇内容将详细分析Harris角点的定义、计算方法、特点。
一、Harris角点定义

在图像中,若以正方形的小像素窗口为基本单位,按照上图可以将它们划分三种类型如下:
- 平坦区域:在任何方向上移动窗口,窗口内容变化都不大
- 边缘:在某一方向上移动窗口,窗口内容变化较大(如图中上下移动基本不变,而左右移动时窗口内容变化较大)
- 角点:在任何方向上移动窗口,窗口内容变化都很大
从人类角度直观理解,图像的关键特征点应该是那些与周围图像存在明显差异的点。
(以灰度图为例,其实就是该点的灰度值与周围点差别较大,那么就可以通过计算其与周围点的灰度差值,即导数来判断)。
以像素窗口为基本单位时,我们将这些与周围图像差异较大的小窗口称为角点,用它们就可以代表图像中具有辨别性的、关键特征区域。
二、Harris角点计算方法
1. 计算窗口内容差异情况
角点是指与周围存在较大内容差异的像素窗口,那么我们首先要给出小窗口与周围窗口的差异情况的计算方法,在方向(u,v)上移动称之为窗口响应值E(u,v)

E(u,v)=∑x,yw(x,y)[I(x+u,y+v)−I(x,y)]2E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
- 红色小窗口为原始窗口用I(x,y)表示,绿色为移动后的窗口I(x+u,y+v),其中(u,v)其实便代表了移动的方向。
- w(x,y)代表了原始窗口中不同像素点的权重
- 公式含义即为将移动前后每个像素的灰度值差求平方,并根据各像素点权重求和作为两个窗口的内容差异E(u,v)
2.窗口内容差异E =》由矩阵M决定
为了更方便的计算窗口在移动前后的响应值,我们将E(u,v)的公式进行一系列的数学变换,首先是做二元泰勒展开:

展开式前两项为0,最后一项可以通过矩阵的形式表示为:
E(u,v)≈[uv]M[uv]E(u,v) ≈ \begin{bmatrix} u&v\end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix}E(u,v)≈[uv]M[uv]
M=∑x,yw(x,y)[Ix2IxIyIxIyIy2]M=\sum_{x,y}w(x,y)\begin{bmatrix}I_{x}^2&I_xI_y\\ I_xI_y&I_{y}^2\end{bmatrix}M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]
根据公式我们发现,E(u,v)的取值即窗口在不同方向(u,v)移动后的相对差异情况关键取决于矩阵M,即不用关心方向(u,v),而是通过矩阵M就可以判断是否为角点(IxI_xIx代表在x方向上的梯度)
3.窗口内容差异E =》由矩阵M决定 =》由特征值λ决定
通过矩阵M判断角点可以进一步简化为通过矩阵M的特征值λ来判断。
当M可以变化为对角矩阵时(不能对角化的情况稍后说明),E(u,v)最终结果为u2λ1+v2λ2u^{2}λ_{1}+v^{2}λ_{2}u2λ1+v2λ2,假设取值为常数c(取1),即有:

E(u,v)=[uv][λ100λ2][uv]=u2λ1+v2λ2E(u,v)=\begin{bmatrix} u&v\end{bmatrix} \begin{bmatrix}λ_{1}&0\\0&λ_{2}\end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}=u^{2}λ_{1}+v^{2}λ_{2}E(u,v)=[uv][λ100λ2][uv]=u2λ1+v2λ2
u2λ1+v2λ2=1\frac{u^2}{λ_{1}}+\frac{v^2}{λ_{2}}=1λ1u2+λ2v2=1
该方程的几何表示为椭圆如下:

- 即当在以长短轴为方向的坐标系上,椭圆边界线上为移动后具有相同响应值E(u,v)的点;
- 即当要让窗口移动后具有相同响应值(内容差异),沿短轴方向移动最短距离,沿长轴移动需要的距离最长——代表短轴是梯度变化最快的方向,长轴是梯度变化最慢方向
若二阶矩矩阵M不能直接对角化时,我们可以将其转为以下形式:
M=R−1[λ100λ2]RM=R^{-1} \begin{bmatrix}λ_1&0\\0&λ_2 \end{bmatrix}RM=R−1[λ100λ2]R
其中R为旋转矩阵,即此时几何表示为发生了旋转的椭圆,而长短轴依然代表梯度变化最慢和最快的方向:

因此,根据角点的定义可知——任何方向上都有较大梯度变化 =》椭圆的长短轴都要短 =》特征值λ1λ_{1}λ1、λ2λ_{2}λ2都要大

- 当λ1λ_{1}λ1、λ2λ_{2}λ2都大,在任何方向梯度都大、E增加的快,即为角点
- 当λ1λ_{1}λ1、λ2λ_{2}λ2其中一个远比另一个大,则说明在最快方向变化特快、同时有一个方向几乎不变,这是边缘区域
- 当λ1λ_{1}λ1、λ2λ_{2}λ2都很小,在任何方向梯度逗笑、E变化的慢,即为平坦区域
4.窗口内容差异E =》由矩阵M决定 =》由特征值λ决定 =》由计算R决定
R由特征值λ1λ_{1}λ1、λ2λ_{2}λ2计算得到,公式为:
R=Det(M)−α∗Trace(M)2=λ1λ2−α(λ1+λ2)2R=Det(M)-α*Trace(M)^2=λ_{1}λ_{2}-α(λ_{1}+λ_{2})^2R=Det(M)−α∗Trace(M)2=λ1λ2−α(λ1+λ2)2
可知当λ1λ_{1}λ1、λ2λ_{2}λ2分别处于3中所说的三种状态时,对应R有:

- 当λ1λ_{1}λ1、λ2λ_{2}λ2都大,R>0,即为角点
- 当λ1λ_{1}λ1、λ2λ_{2}λ2其中一个远比另一个大,R<0,这是边缘区域
- 当λ1λ_{1}λ1、λ2λ_{2}λ2都很小,R接近0,即为平坦区域
三、Harris角点的特点

上图为使用Harris角点检测获取的关键点。
对于理想的图像特征点,应该可以抵抗光照、旋转、平移、尺度等变化,即具有不变性(Invariance)或协变性(Covariance)
- 不变性(Invariance):变换后原特征点仍能被检测出来、且位置不变;
- 协变性(Covariance):变换后原特征点仍能被检测出来,但位置可能发生变化
3.1 优点
针对Harris角点来说,能够抵抗光照、旋转、平移变换(该部分图片来自知乎@饭饭):

光照:光照变换会使得区域像素灰度值整体提高或降低
- 当增量或这减量相同(灰度平移)时,对基于像素间灰度差值(梯度)的角点判断方法不影响,已经被检测出来的角点能够保持不变性。
- 当相比原来灰度成倍增加或减少(尺度平移),阈值不变时可能导致检测角点的数量增加或减少,但同时被检测出的相同角点位置不变

旋转:当发生旋转时,相当于二阶矩矩阵对应几何椭圆旋转(即梯度变化最快最慢的方向发生变化),但特征值不变,角点本身只有位置可能发生了变化,即具有协变性
平移:与旋转类似,角点位置发生变化,具有协变性,但梯度变化最快最慢方向不变
3.2 缺点
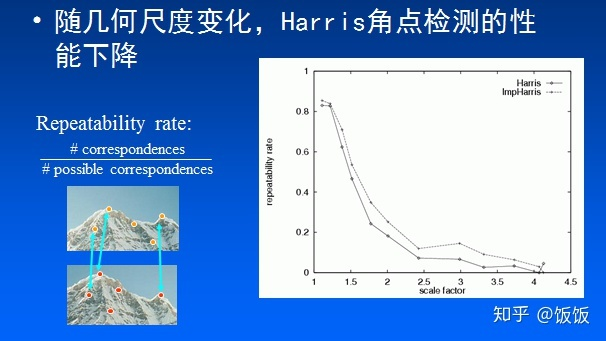
Harris角点并不具有尺度不变性,当图像尺度缩小时,原来的角点区域可能被判断为边缘、甚至进一步平坦区域;反之尺度放大时也会导致原角点找不到对应角点的情况出现;为了在此基础上保持尺度不变性,可以使用后续的SIFT特征检测方法。
相关文章:

【仔细理解】计算机视觉基础1——特征提取之Harris角点
Harris角点是图像特征提取中最基本的方法,本篇内容将详细分析Harris角点的定义、计算方法、特点。 一、Harris角点定义 在图像中,若以正方形的小像素窗口为基本单位,按照上图可以将它们划分三种类型如下: 平坦区域:在任…...
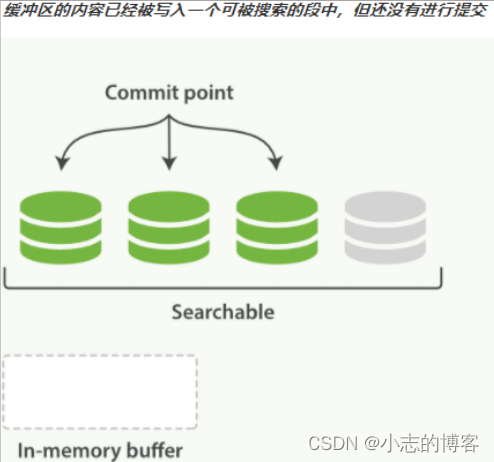
Elasticsearch7.8.0版本进阶——近实时搜索
目录一、近实时搜索的概述1.1、按段(per-segment)搜索1.2、更轻量的方式搜索二、为什么Elasticsearch是 近 实时搜索三、如何解决索引了一个文档然后却没有搜到四、哪种情况不需要每秒刷新4.1、使用 Elasticsearch 索引大量的日志文件4.2、使用 Elastics…...
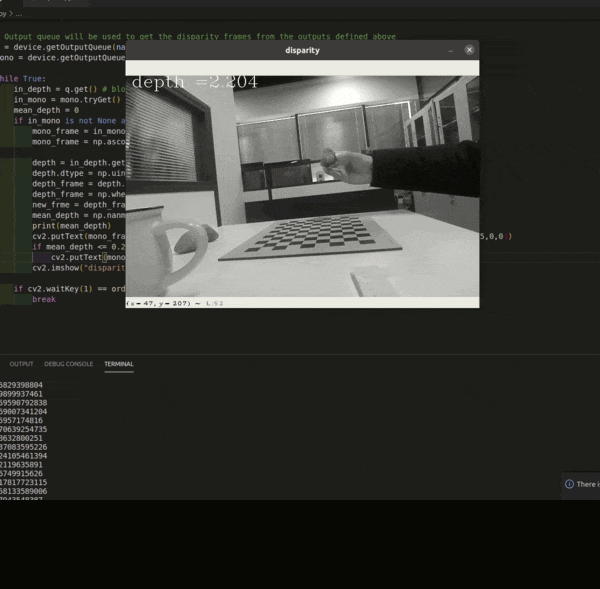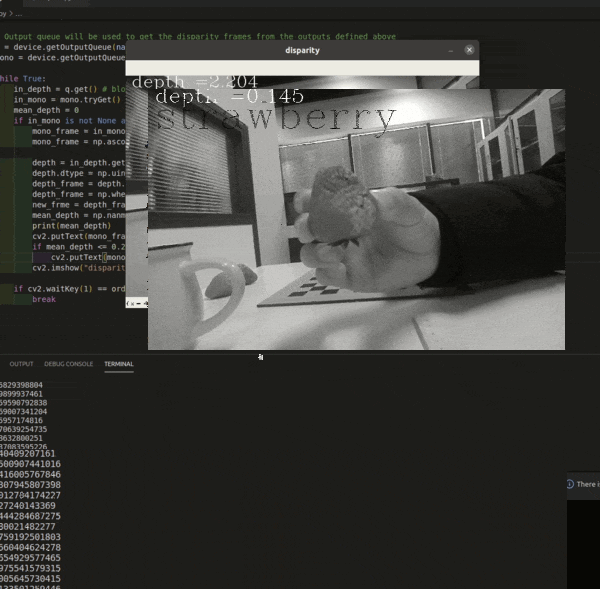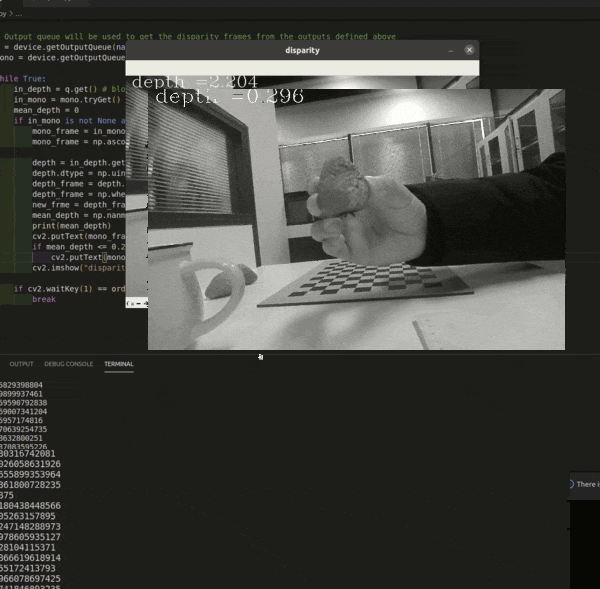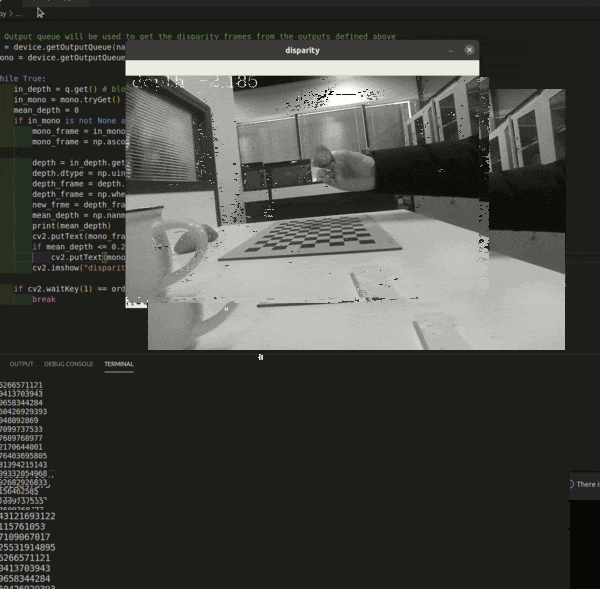
OAK相机深度流探测草莓距离
编辑:OAK中国 首发:oakchina.cn 喜欢的话,请多多👍⭐️✍ 内容可能会不定期更新,官网内容都是最新的,请查看首发地址链接。 ▌前言 Hello,大家好,这里是OAK中国,我是助手…...
的相关知识及指令)
文件共享服务器(CIFS)的相关知识及指令
文件共享服务器(CIFS) 微软开发的 共享服务器概述 通过网络提供文件共享拂去,提供文件下载和上传服务(类似于FTP服务器) 创建共享 通过本地登录时,仅受NTFS权限的控制通过网络访问时,受共享…...

springcloud-2service consumer
创建使用会员微服务模块-service consumer思路分析/图解创建Moduel(member-service-consumer-80) & 完成配置new Module->member-service-consumer-80->finish检查父子项目的pom是否添加相应的对应module和parent本项目的pom.xml可以参考provider的,并删掉…...
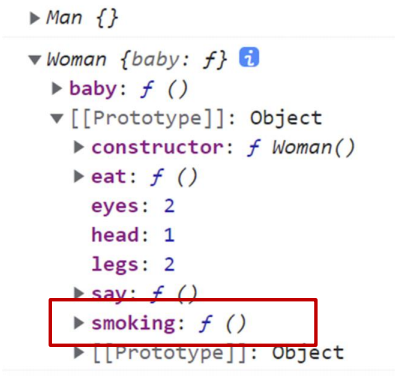
JavaScript 进阶--charater3
文章目录前言一、编程思想1.1 面向过程介绍1.2 面向对象编程 (oop)对比二、构造函数三、原型3.1原型3.2 constructor 属性3.3 对象原型3.4 原型继承3.5 原型链总结前言 🆑学习目标 理解面向对象思想,掌握函数原型对象运用面向对象封装继承特点…...

Solon2 之基础:三、启动参数说明
启动参数,在应用启动后会被静态化(为了内部更高效的利用)。比如,想通过体外扩展加载配置,是不能改掉它们的。 1、启动参数 启动参数对应的应用配置描述–envsolon.env环境(可用于内部配置切换)…...

引入防关联浏览器以防止数据盗窃
目前,互联网已成为我们生活中不可缺少的且不断发展的一部分。因此,互联网变得更加复杂和多样化,每天都有新的技术、服务和应用推出。在这个不断变化的环境中,虚拟浏览器最近作为一种革命性的新方式出现在互联网上。 简而言之&…...
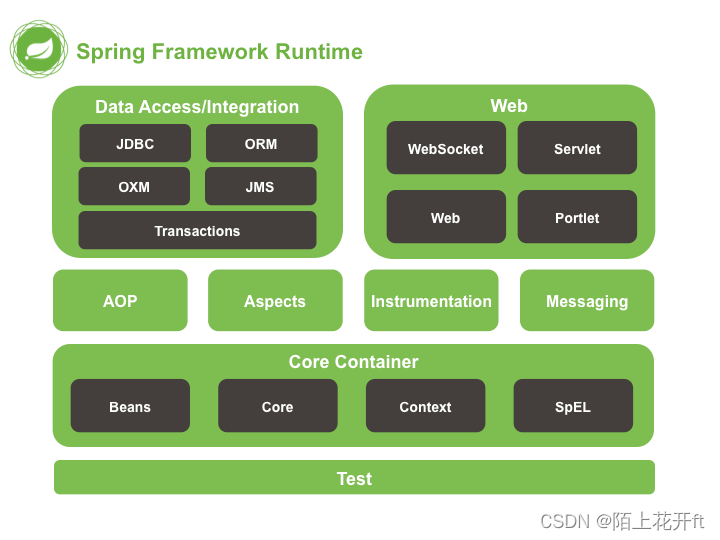
Spring的一些知识点
什么是Spring? Spring是一种轻量级的开发框架,旨在提高开发人员的开发效率以及系统的可维护性。 Spring的核心模块 Spring Core是基础模块,可以说Spring的其他功能都要依赖于该类库,主要提供IOC的依赖注入功能; Spri…...
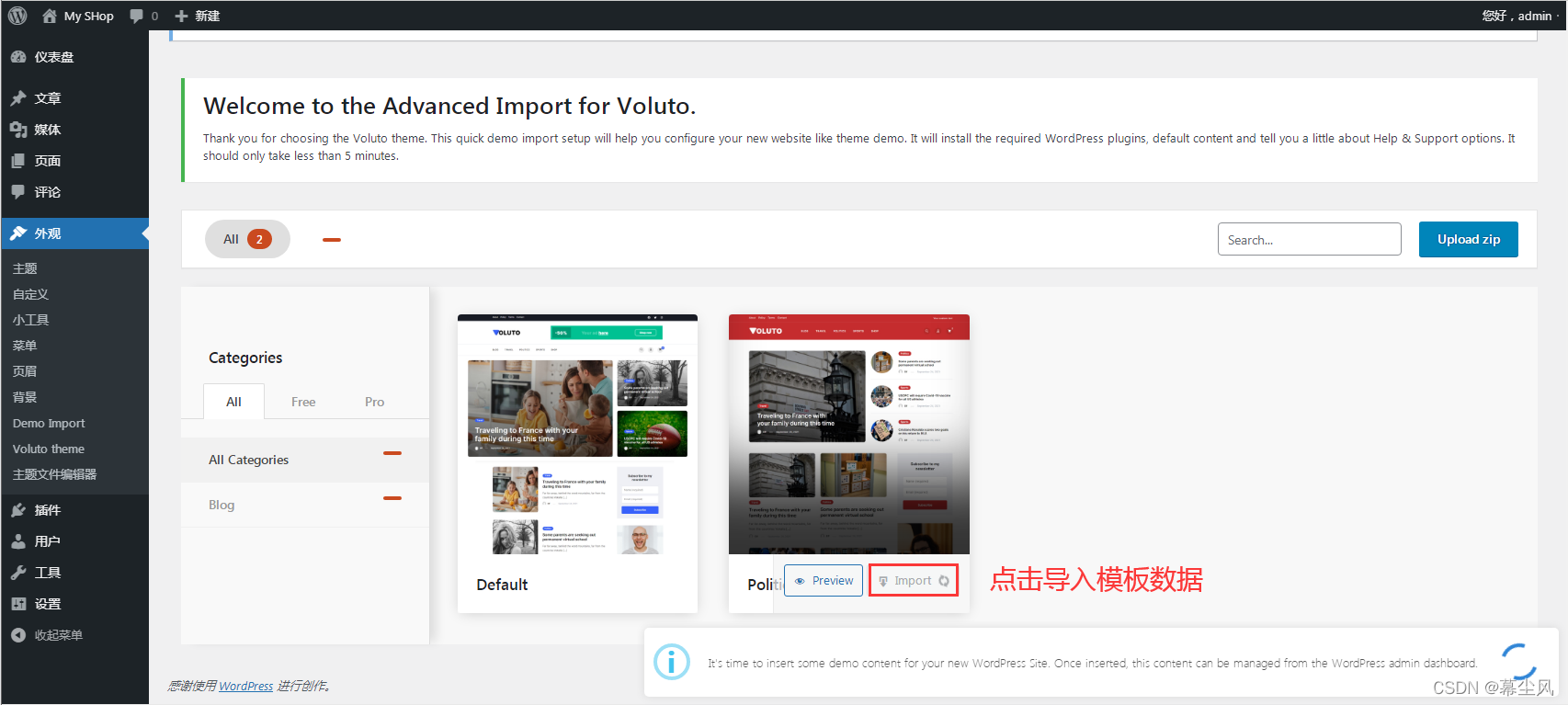
使用WordPress快速搭建外贸网站教程
一、下载安装 1、首先前往官方下载wordPress框架,下载地址:Download | WordPress.org 2、把下载好的安装包上传到我们的服务器,解压 3、我使用的搭建环境是宝塔Linux CentOS 7.9(Apache2.4mysql5.6php7.4)…...

在 vue 或 react 项目中使用 mockjs 搭建 mock server
有时候,在公司里一些项目开发前,后端接口没那么快给到前端时,前端可以先跟后端约定好各个接口的请求路径、请求参数以及返回数据格式,先整理出一份接口文档,这样前端可以通过mockjs参考接口文档,自己先模拟…...

【十一届蓝桥杯】
ans 0for i in range(1,2021):ans (str(i).count(2))print(ans)第二个def check(s):return s 2020matrix []s input()while 1 not in s:matrix.append(list(s))s input()n,m len(matrix),len(matrix[0])ans 0for i in range(n):for j in range(m):if i 3 < n and c…...
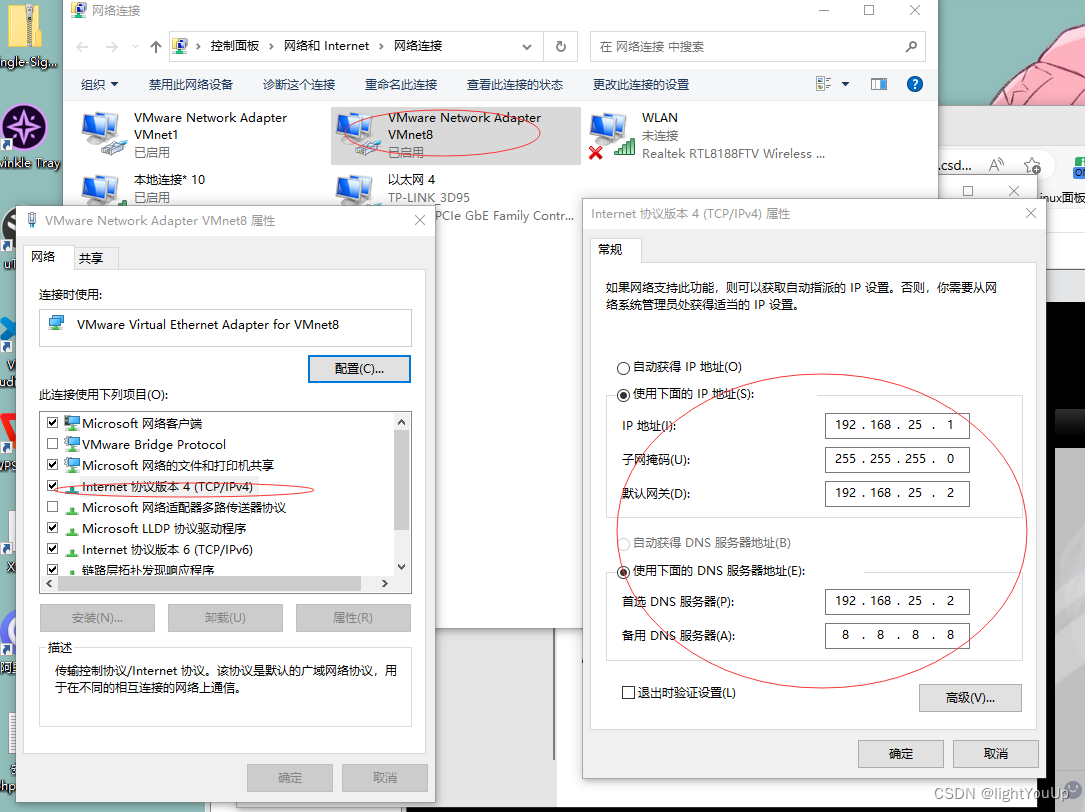
vm 网络配置
点击NAT设置,配置本台虚拟机ip(注意网关要在同一个网段),配置对应端口 然后添加映射端口: 然后选择网络适配器 选择vm8网卡 配置网卡静态ip #查看网卡 ip addr #修改网卡配置 cd /etc/sysconfig/network-scripts…...
)
2023年CDGA考试-第11章-数据仓库和商务智能(含答案)
2023年CDGA考试-第11章-数据仓库和商务智能(含答案) 单选题 1.商务智能是在构建好数据仓库以后,支撑业务决策 风险管理等更高层面的分析,以下描述不符合的是: A.提供数据查询、分析和报表等珈能 B.通过收集。整合 分析和探索数据来支持决策 C.对数据进行可视化 D.从数据中…...

从0-1搭建流媒体系统之live555 安装、运行、转发、拉流
流媒体开发系列文章 文章目录 流媒体开发系列文章前言一、环境准备?二、安装编译过程三、vscode调试代码四、代码分析总结前言 目前、比较有名的流媒体服务器有ZLMediaKit、srs、live555、eadydarwin等。因为srs是单线程服务、对于多核服务器的支持需要通过部署多个服务来充分…...
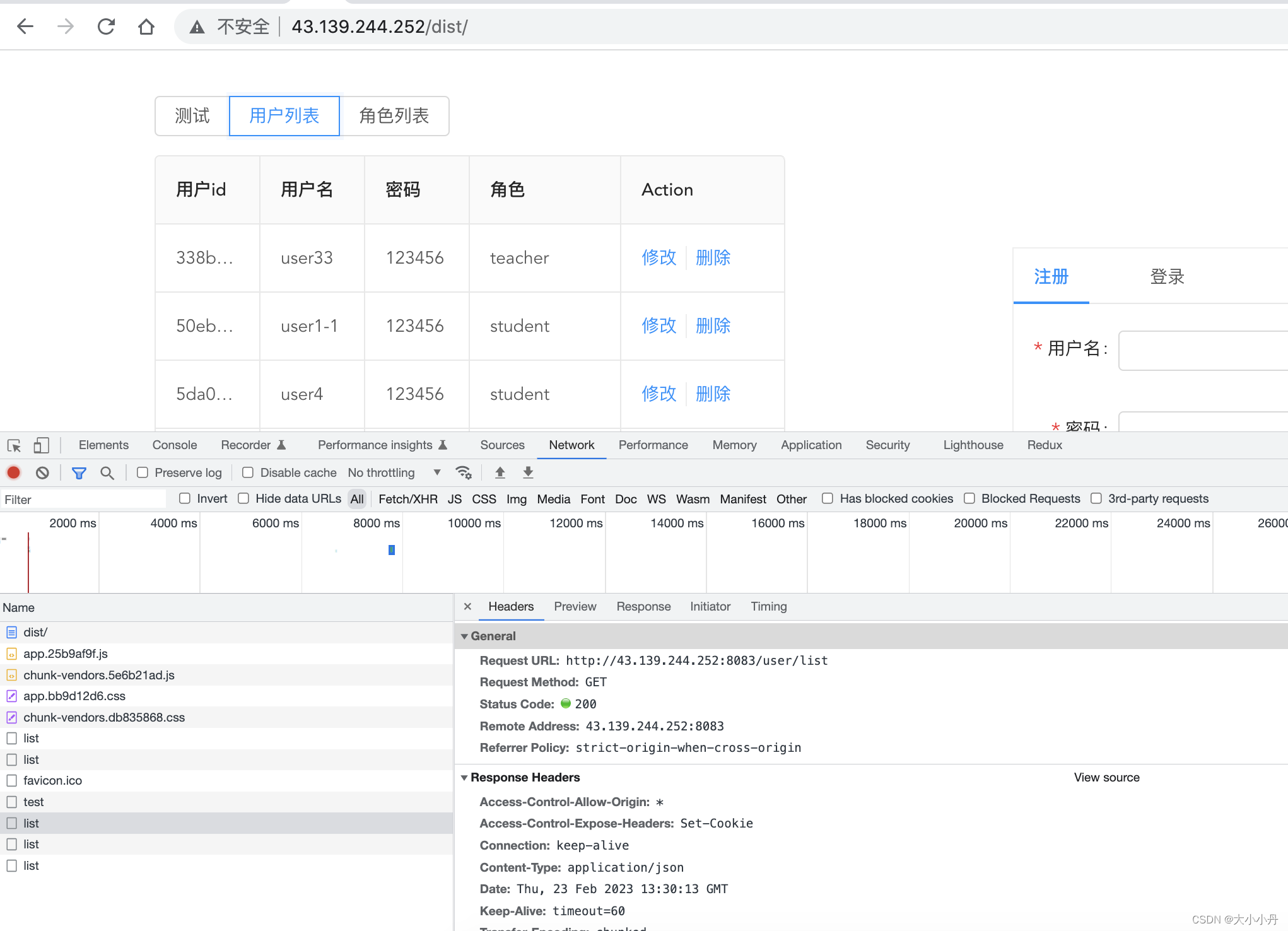
搭建个人博客保姆级教程(二)
文章目录一. Springboot项目打包成jar包二. mySql部署三. UI 项目部署一. Springboot项目打包成jar包 使用IDEA进行打包,当然也有其他部署方式,如使用maven进行打包,可自行查询资料。 1.打开项目,右击项目选中Open Module Settin…...

数字图像处理与Python实现-Pillow图像处理
Pillow图像处理 文章目录 Pillow图像处理1、Pillow介绍2、 Pillow 中的Image模块和Image类2.1 读取图像2.2 图像大小调整2.3 图像保存2.4 图像旋转2.5 图像储存模式与转换3、图像滤波处理3.1 使用卷积核进行滤波3.2 图像模糊、锐化和平滑3.3 边缘检测、边缘增强和浮雕效果3.4 图…...

HMM隐马尔可夫模型 | 关键原理+面试知识点
😄 HMM之前跟人生导师:李航学习过,这里结合自己的理解,精简一波HMM,总结一下面试中高频出现的要点。 文章目录 1、何为HMM?2、HMM三要素:3、HMM两大强假设4、HMM三个基本问题 :5、HMM中涉及的算法6、HMM缺点7、面试高频题7.1、HMM中为何引入维特比算法作为预测算法?…...

【Leedcode】数据结构中链表必备的面试题(第三期)
【Leedcode】数据结构中链表必备的面试题(第三期) 文章目录【Leedcode】数据结构中链表必备的面试题(第三期)一、第一题1.题目2.思路3.源代码二、第二题1.题目2.思路(1)第一种情况:偶数个链表(2)第二种情况:…...
【数学,二分,暴力,思维】)
D1.Chopping Carrots (Easy Version)【数学,二分,暴力,思维】
链接 理论基础 已知正整数a,v,求证m⌊av⌋是满足⌊am⌋⩾v的最大的m,其中x是正整数已知正整数a,v,求证m\lfloor \frac {a}{v} \rfloor是满足\lfloor \frac {a}{m} \rfloor \geqslant v的最大的m,其中x是正整数已知正整数a,v,求证m⌊va⌋是满足⌊ma⌋…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
