博弈论——伯特兰德寡头模型(Bertrand Model)
伯特兰德寡头模型(Bertrand Model)
0 引言
在前面几篇文章中,我们介绍了古诺模型(Cournot duopoly model)和斯塔克尔伯格模型(Stackelberg model)
博弈论——连续产量古诺模型(Cournot duopoly model)
博弈论——斯塔克尔伯格模型(Stackelberg model)
这两个模型都是把厂商的产量作为竞争手段,是一种产量竞争模型,也就是说博弈方的决策变量都是产量,而伯特兰德模型是价格竞争模型。
同时我们也介绍了反应函数法:得益是策略多元连续函数的博弈,都可以求每个博弈方的反应函数,解出各博弈方反应函数的交点就是纳什均衡。这种用反应函数求纳什均衡的方法,称为“反应函数法”。我们也分别用反应函数对古诺模型和斯塔克尔伯格模型进行了求解。
在这篇文章中,我们将继续推进反应函数法的使用,利用该方法来求解伯特兰德模型。
1 伯特兰德寡头模型
1.1 模型建立
在伯特兰德价格博弈模型中,两寡头生产有一定差别的产品。产品差别指在品牌、质量和包装等方面有所不同的同类产品,有很强的替代性,但又不是完全可替代。最后,仍强调两个厂商是同时决策的。假设厂商1生产产品1,厂商2生产产品2。
产品价格:P1、P2分别为厂商1、厂商2的产品价格;
潜在市场规模:a1、a2分别为产品1、产品2的潜在市场规模;
生产成本:假设两个厂商无固定成本,边际生产成本分别为c1和c2;
价格弹性:b1、b2为产品1、产品2的价格弹性;
产品的替代系数:d1、d2为两个产品的替代系数。
根据上述参数设置,我们得到了以下的模型:
假设当厂商1和厂商2价格分别为P1和 P2时,各自的需求函数为:
q 1 = q 1 ( P 1 , P 2 ) = a 1 − b 1 P 1 + d 1 P 2 q_1=q_1 (P_1,P_2 )=a_1-b_1 P_1+d_1 P_2 q1=q1(P1,P2)=a1−b1P1+d1P2
q 2 = q 2 ( P 1 , P 2 ) = a 2 − b 2 P 2 + d 2 P 1 q_2=q_2 (P_1,P_2 )=a_2-b_2 P_2+d_2 P_1 q2=q2(P1,P2)=a2−b2P2+d2P1
在该博弈中,两博弈方的决策变量为产品价格,因此各自的策略空间为 s 1 = [ 0 , P 1 m a x ] s_1=[0,P_{1max}] s1=[0,P1max]和 s 2 = [ 0 , P 2 m a x ] s_2=[0,P_{2max}] s2=[0,P2max],其中 P 1 m a x P_{1max} P1max和 P 2 m a x P_{2max} P2max是厂商1和厂商2还能卖出产品的最高价格。两博弈方的得益是各自的利润,即销售收益减去成本,它们都是双方价格的函数为:
π 1 = π 1 ( P 1 , P 2 ) = P 1 q 1 − c 1 q 1 = ( P 1 − c 1 ) ( a 1 − b 1 P 1 + d 1 P 2 ) π_1=π_1 (P_1,P_2 )=P_1 q_1-c_1 q_1=(P_1-c_1)(a_1-b_1 P_1+d_1 P_2) π1=π1(P1,P2)=P1q1−c1q1=(P1−c1)(a1−b1P1+d1P2)
π 2 = π 2 ( P 1 , P 2 ) = P 2 q 2 − c 2 q 2 = ( P 2 − c 2 ) ( a 2 − b 2 P 2 + d 2 P 1 ) π_2=π_2 (P_1,P_2 )=P_2 q_2-c_2 q_2=(P_2-c_2)(a_2-b_2 P_2+d_2 P_1) π2=π2(P1,P2)=P2q2−c2q2=(P2−c2)(a2−b2P2+d2P1)
1.2 模型求解
我们用反应函数法分析这个博弈。对上述得益函数求偏导,并且偏导为0时存在最大值:
∂ π 1 ∂ P 1 = − 2 b 1 P 1 + c 1 b 1 + a 1 + d 1 P 2 \frac{∂π_1}{∂P_1}=-2b_1 P_1+c_1 b_1+a_1+d_1 P_2 ∂P1∂π1=−2b1P1+c1b1+a1+d1P2
∂ π 2 ∂ P 2 = − 2 b 2 P 2 + c 2 b 2 + a 2 + d 2 P 1 \frac{∂π_2}{∂P_2}=-2b_2 P_2+c_2 b_2+a_2+d_2 P_1 ∂P2∂π2=−2b2P2+c2b2+a2+d2P1
令 ∂ π 1 ∂ P 1 = 0 \frac{∂π_1}{∂P_1}=0 ∂P1∂π1=0, ∂ π 2 ∂ P 2 = 0 \frac{∂π_2}{∂P_2}=0 ∂P2∂π2=0得到两个厂商的反应函数为:
P 1 = R 1 ( P 2 ) = 1 2 b 1 ( c 1 b 1 + a 1 + d 1 P 2 ) P_1=R_1 (P_2 )=\frac{1}{2b_1} (c_1 b_1+a_1+d_1 P_2) P1=R1(P2)=2b11(c1b1+a1+d1P2)
P 2 = R 2 ( P 1 ) = 1 2 b 2 ( c 2 b 2 + a 2 + d 2 P 1 ) P_2=R_2 (P_1 )=\frac{1}{2b_2}(c_2 b_2+a_2+d_2 P_1) P2=R2(P1)=2b21(c2b2+a2+d2P1)
回顾一下我们在反应函数文章中的介绍,该博弈的纳什均衡是两条反应函数对应图像的交点 ( P 1 ∗ , P 2 ∗ ) (P_1^*,P_2^*) (P1∗,P2∗),并且这个交点需要满足:
P 1 ∗ = 1 2 b 1 ( c 1 b 1 + a 1 + d 1 P 2 ∗ ) P_1^*=\frac{1}{2b_1} (c_1 b_1+a_1+d_1 P_2^*) P1∗=2b11(c1b1+a1+d1P2∗)
P 2 ∗ = 1 2 b 2 ( c 2 b 2 + a 2 + d 2 P 1 ∗ ) P_2^*=\frac{1}{2b_2}(c_2 b_2+a_2+d_2 P_1^*) P2∗=2b21(c2b2+a2+d2P1∗)
解上述的二元一次方程组,得:
P 1 ∗ = d 1 ( a 2 + b 2 c 2 ) + 2 b 2 ( a 1 + c 1 b 1 ) 4 b 1 b 2 − d 1 d 2 P_1^*=\frac{d_1 (a_2+b_2 c_2 )+2b_2 (a_1+c_1 b_1)}{4b_1 b_2-d_1 d_2} P1∗=4b1b2−d1d2d1(a2+b2c2)+2b2(a1+c1b1)
P 2 ∗ = d 2 ( a 1 + c 1 b 1 ) + 2 b 1 ( a 2 + b 2 c 2 ) 4 b 1 b 2 − d 1 d 2 P_2^*=\frac{d_2 (a_1+c_1 b_1 )+2b_1 (a_2+b_2 c_2)}{4b_1 b_2-d_1 d_2} P2∗=4b1b2−d1d2d2(a1+c1b1)+2b1(a2+b2c2)
则 ( P 1 ∗ , P 2 ∗ ) (P_1^*,P_2^*) (P1∗,P2∗)为该博弈的唯一纳什均衡。将 P 1 ∗ 、 P 2 ∗ P_1^*、P_2^* P1∗、P2∗代入得益函数中,可以求得两个厂商的均衡得益,这里我就不再赘述了,有兴趣的读者可以自行代入计算。
谢老师的书中,对该模型的各参数做了具体假设: a 1 = a 2 = 28 , b 1 = b 2 = 1 , d 1 = d 2 = 0.5 , c 1 = c 2 = 2 a_1=a_2=28,b_1=b_2=1,d_1=d_2=0.5,c_1=c_2=2 a1=a2=28,b1=b2=1,d1=d2=0.5,c1=c2=2,则可以解得 P 1 ∗ = P 2 ∗ = 20 , u 1 ∗ = u 2 ∗ = 324 P_1^*=P_2^*=20,u_1^*=u_2^*=324 P1∗=P2∗=20,u1∗=u2∗=324。
2 总结
更一般的伯特兰德模型可以有n个寡头,产品也可以是无差别的。产品无差别时,可以考虑消费者对价格的敏感性问题。因为如果所有消费者对价格都非常敏感,则生产无差别产品的厂商中价格高的一方完全卖不出去,价格差别不可能存在。多寡头伯特兰德模型的分析是两寡头模型的简单推广,只需求出每个厂商对其他各个厂商价格的反应函数,解出它们的交点即可。
相关文章:
)
博弈论——伯特兰德寡头模型(Bertrand Model)
伯特兰德寡头模型(Bertrand Model) 0 引言 在前面几篇文章中,我们介绍了古诺模型(Cournot duopoly model)和斯塔克尔伯格模型(Stackelberg model) 博弈论——连续产量古诺模型(Cournot duopoly model) 博弈论——斯塔克尔伯格模型(Stackelberg model) 这两个模型…...

第一百六十回 SliverPadding组件
文章目录 概念介绍使用方法示例代码 我们在上一章回中介绍了SliverAppBar组件相关的内容,本章回中将介绍 SliverPadding组件.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在本章回中介绍的SliverPadding组件类似Pading组件,它主要用…...
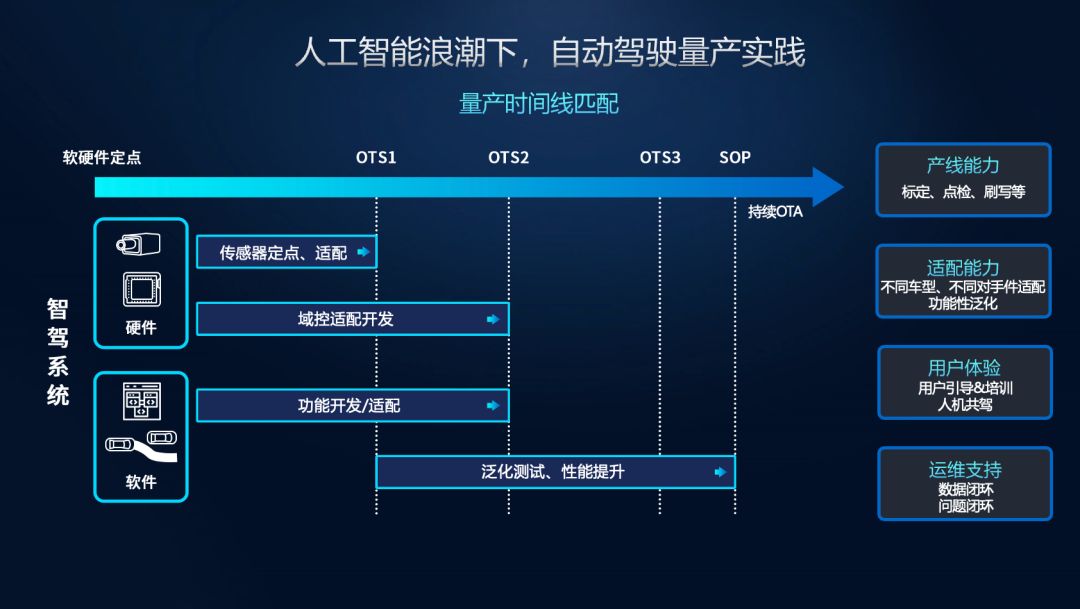
Mapfree智驾方案,怎样实现成本可控?
整理|睿思 编辑|祥威 编者注:本文是HiEV出品的系列直播「智驾地图之变」第二期问答环节内容整理。 元戎启行副总裁刘轩与连线嘉宾奥维咨询董事合伙人张君毅、北汽研究总院智能网联中心专业总师林大洋、主持嘉宾周琳展开深度交流,并进行了答疑。 本期元…...
javascript: Bubble Sort
// Sorting Algorithms int JavaScript /** * file Sort.js * 1. Bubble Sort冒泡排序法 */ function BubbleSort(arry, nszie) {var i, j, temp;var swapped;for (i 0; i < nszie - 1; i){swapped false;for (j 0; j < nszie - i - 1; j){if (arry[j] > arry[j …...

DM数据库根据rowid删除重复的记录
oracle中rowid的用法-CSDN博客 delete from stu a where rowid not in (select max(b.rowid) from stu b where a.nob.no and a.name b.name and a.sex b.sex); //这里max使用min也可以...

【AI视野·今日Robot 机器人论文速览 第四十期】Mon, 25 Sep 2023
AI视野今日CS.Robotics 机器人学论文速览 Mon, 25 Sep 2023 Totally 36 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚CloudGripper, 一套云化的机器抓取人数据采集系统,包含了32个机械臂的集群。(from KTH Royal Institute of Te…...
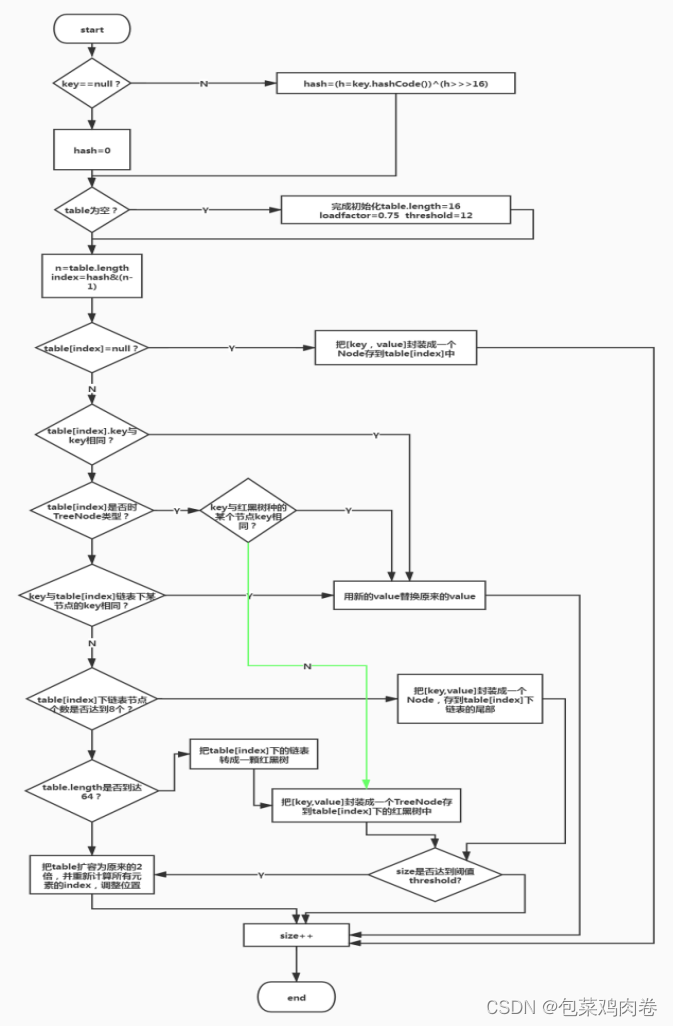
HashMap底层源码,数据结构
HashMap的底层结构在jdk1.7中由数组链表实现,在jdk1.8中由数组链表红黑树实现,以数组链表的结构为例。 JDK1.8之前Put方法: JDK1.8之后Put方法: HashMap基于哈希表的Map接口实现,是以key-value存储形式存在,…...

计算机等级考试—信息安全三级真题八
一、单选题...
番外6:下载+安装+配置Linux
#########配置Linux---后续 step08: 点击编辑虚拟机设置,选择下载好的映像文件.iso进行挂载; step09: 点击编辑虚拟机选项,选择UEFI启动模式并点击确定; step10: 点击开启虚拟机,选择Install rhel ; 备注&…...
方法和他的属性)
javascript验证表单字段有效性,使用checkValidity()方法和他的属性
<script type"text/javascript">function LoginCheckValidity(){var txt"";var rmb1document.getElementById("rmb1");if(rmb1.checkValidity()false){if(rmb1.validitionMessageundefined){txt"输入金额有误,金额10-200之间";}…...
pdf怎么调整大小kb?pdf文件过大这样压缩
在日常的工作和生活中,我们常常会遇到需要调整PDF文件大小的问题。有时候,我们需要将大型的PDF文件上传到某些平台,但平台的限制让我们不得不压缩文件的大小。那么,如何有效地调整PDF文件的大小呢? 一、使用嗨格式压缩…...

vue3中的watch
在Vue3中,watch中的参数可以分为两部分,即要监听的响应式数据以及回调函数。 语法格式如下: watch(要监听的响应式数据, 回调函数)除了以上的两个还有其他的参数 immediate:是否在初始化时立即执行一次回调函数,默认…...
开绕组电机零序Bakc EMF-based无感控制以及正交锁相环inverse Park-based
前言 最近看论文遇到了基于反Park变换的锁相环,用于从开绕组永磁同步电机零序电压信号中提取转子速度与位置信息,实现无感控制。在此记录 基于零序Back EMF的转子估算 开绕组电机的零序反电动势 e 0 − 3 ω e ψ 0 s i n 3 θ e e_0-3\omega_e\psi_…...
番外5:下载+安装+配置Linux
任务前期工作: 01. 电脑已安装好VMware Workstation软件; 02.提前下载好Rhel-8.iso映像文件(文件较大一般在9.4GB,建议采用迅雷下载),本人使用的以下版本(地址ed2k://|file|rhel-8.4-x86_64-dvd…...

新手--安装好Quartus II13.0(带modelsim集成包)并用Quartus II搭建一个工程
前言 今天是国庆节,我们正式来学习Quartus II13.0软件的安装与使用。学习verilog与学习C语言都是学习一门语言,那么学习一门语言,光看理论不敲代码绝对是学习不好的。要用verilog语言敲代码,就要像C语言那样搭建起语言的编译环境&…...

python监控软件内存、cpu和GDI
目录 前言代码 前言 最近做软件测试需要监控软件内存、cpu和GDI对象数,用psutil库可以很方便的实现监控内存和CPU,但是GDI好像还不行,最后来的win32api来调用的Windows API接口来实现GDI监控的,在此做个记录。 代码 import psu…...

wordpress搭建自己的博客详细过程以及踩坑
WordPress作为一款开源的内容管理系统(CMS),具有诸多优势。首先,它的易用性使得即使对于没有编程经验的用户来说也能轻松上手,通过直观的用户界面和友好的管理工具,用户可以方便地创建、编辑和发布内容。其…...

在jupyter中更改、增加内核
今天在配置llama2的环境,在学院实验室的服务器上面用jupyter,怎么都不会增加内核。今天说一下怎么把创建好的conda环境增加到jupyter列表中。 例如我有个环境叫做llama2,很简单只要两步。 第一步先激活conda环境。 conda activate llama2第…...
Redis代码实践总结(二)
使用 CLI 探索 Redis 外部程序使用 TCP 套接字和 Redis 特定协议与 Redis 进行通信。该协议在不同编程语言的 Redis 客户端库中实现。然而,为了使使用 Redis 进行黑客攻击变得更简单,Redis 提供了一个命令行实用程序,可用于向 Redis 发送命令…...
读取一张图片各种颜色占比
提问之初 <small> 读取一张图片各种颜色占比 /storage/emulated/0/Pictures/Screenshots/Screenshot_20230725_195440.jpg有趣优雅热情沉着的代码与注释/每行每行 from PIL import Image # 导入PIL大法,这是处理图像的必备神器# 图片路径,此处为…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
