排序算法之【希尔排序】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

前言
希尔排序,作为一种高效的排序算法,更是在排序算法这个舞台上展现出了自己独特的魅力,听这个名字就感觉这个排序不简单,本篇文章我将带领大家深入了解希尔排序。
1. 排序算法
在数据世界中,排序算法是一种强大的工具,能够将混乱无序的数据变得井然有序,排序算法有很多种,最常见也是最常用的排序算法有8种,本期的主角是希尔排序。
1.1插入排序
希尔排序属于插入排序的一种,在理解希尔排序之前,我们需要先来了解一下插入排序的初阶——直接插入排序
1.1.1 直接插入排序
直接插入排序的原理非常好理解,举个例子:我们在完扑克牌时都会对牌的大小进行排序(也就是组成顺子)。

这就利用了直接直接插入排序,7和10比较,7小,7再和5比较,比5大,所以7就插入到10的前边。
直接插入排序,是一种简单直观的排序算法,它的基本思想是将一个待排序的元素插入到已经排好序的元素序列中的适当位置,从而得到一个新的、个数加一的有序序列。具体步骤如下:
- 将待排序序列第一个元素视为已排序序列,将其作为比较的基准。
- 从第二个元素开始,依次将每个元素插入到已排序序列中的适当位置。
- 每次插入一个元素时,都将该元素与已排序序列中的元素进行比较,找到合适的位置插入。
- 插入时,将已排序序列中比待插入元素大的元素向后移动一位,为待插入元素腾出位置。
- 重复步骤3和步骤4,直到将所有元素插入到已排序序列中。
过程如下图:
理解了基本原理,我们来进行代码实现,在写排序算法时我们可以先写一趟的逻辑。我们需要记录开始比较的位置,还要记录开始位置的后一个数据,例如当end=0时,我们需要记录end的后一个位置数据,从end开始一次向前移动并比较大小。如果tmp小于end位置的数据,那么,end位置的数据就向后移动一个位置。在这个过程中end要不断减减。具体代码如下:
int end = ;int tmp = arr[end + 1];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];}else{break;}end--;}arr[end + 1] = tmp;//找到比tmp大的数据后跳出循环插入到end的后边
}这也仅仅是一个数据插入的过程,接下来我们要搞定这个数组所有的元素。我们可以利用一个for循环,观察动图我们可以发现,end是逐个向后的。但我们需要考虑越界的问题,i要小于n-1,结束位置在最后的前一个位置。完整代码如下:
void InsertSort(int* arr,int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];}else{break;}end--;}arr[end + 1] = tmp;}
}1.1.2 希尔排序
由来
通过上述的插入排序过程我们可以发现,插入排序的时间复杂度不低,在局部有序的情况下,插入排序很优。但存在最坏的情况,就是逆序。逆序的情况下,它的时间复杂度不亚于冒泡排序。
为了防止出现较坏的情况,有位叫希尔的大佬对插入排序进行了优化,就是在插入排序之前进行预排序。所以希尔排序的过程就可分为两部分:
- 预排序
- 插入排序
过程
希尔排序(Shell Sort),也称为缩小增量排序,是插入排序的一种改进算法。它通过将待排序序列分割成若干子序列来进行排序,最终将整个序列排序。
希尔排序的基本思想是先将待排序序列按照一定的增量进行分组,对每个子序列进行插入排序,然后逐步缩小增量,再次进行分组和插入排序,直到增量为1,完成最后一次插入排序,整个序列就变成有序的。
预排序
上边说到按照增量进行分组,不好理解,我们可以理解为步数(gap),当gap为1的时候就是插入排序,gap为1就是相邻数据依次比较进行插入。当gap > 1时都是预排序,目的是让数组更接近于有序。
例如gap等于4,那进行比较时就是对相邻间隔为4的数据进行调整位置插入。如下图:
gap越小,数据就越接近有序。
1.1.3 希尔排序的实现
理解了预排序的原理,我们可以先来写一下预排序。
for (int i = 0; i < n - gap; i+=gap)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;
}这段代码看着是否很熟悉,当gap为1时,这段代码就是直接插入排序。这个是从第一个数据开始,将数组中距离为gap数据进行调整。
那么接下来还要从第二个数据开始,将距离为gap的数据进行调整。所以这里我们可以加一个循环,确保每个数据都能被调整。
for (int i = 0; i < gap; i++)
{for (int i = 0; i < n - gap; i+=gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;}
}这里我们可以优化一下,我们这样写:
for (int i = 0; i < n - gap; i++)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;
}大多数看到的书中都是这样写的,或许在之前学习中,很多同学不懂for循环这里为什么这样写。起初的逻辑是,调整完一组后,再调整下一组。那我们可不可以同时调整所有组?
我们先调整第一个数据和它距离为gap的数据,不急着将整组数据调整完,接着开始从第二个数据开始与它距离为gap的数据进行调整……
理解了这里,我们继续,上述的过程是在gap不变的情况下进行的,预排序的过程是不断的改变gap的值来进行预排序。gap越小预排序后数据越接近有序。
void ShellSort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;}}
}我们可以先令gap等于n(数组的数据个数),然后使用while循环判断gap是否大于1,当gap > 1时都是预排序,进入while循环之后,gap就整除2。到这里希尔排序就实现了。任何一个大于2的数除2最后都等于1,除到最后gap等于2时进入while循环,先执行gap=gap/2,最后一次执行时就刚好是插入排序。
当然gap也不一定就除2,在一些书中也有这样的写法:gap=gap/3+1,除3是因为有人觉得gap/2进行预排序的次数太多了,但gap/3并不能保证除到最后,所以就有了这种写法:gap=gap/3+1。
2. 复杂度
了解了直接插入排序和希尔排序,那我们就来说一说它的复杂度问题,它们的空间复杂度都为O(1),重点就在它们的时间复杂度。
2.1 直接插入排序
直接插入排序的时间复杂度好说,假设有n个数据,第一次从第一个数据开始,最多比较1次,第二次从第二个数据开始,最多比较2次,第三个最多比较3次……
那么它的执行次数T=1+2+3+4+……+n-1,等差数列求和,T=(n-1+1)*n/2(首项加尾项乘以项数除以2)所以它的时间复杂度最差达到O(N^2)。
2.2 希尔排序
希尔排序的时间复杂度计算非常复杂,它的时间复杂度和gap有关。
当gap很大时,例如gap=n/3。整个数组逆序那么就有n/3组数据,每组数据最多比较3(1+2)次。
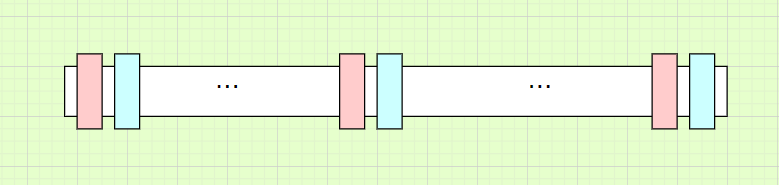
合计比较:n/3*3=n。
当gap等于n/9时,整个数组逆序,就会有n/9组数据,每组有9个数据,每组最多比较(1+2+3+4+5+6+7+8)次
合计比较:n/9*36=4n。
当gap很小时,如gap等于1时,就只有1组数据进行调整排序,此时的数据已经非常接近有序了,再进行调整,最差会比较n次,估算一下,合计:n
由此可以看出:希尔排序的性能图形为一个曲线函数。
希尔排序时间复杂度计算分析,以上内容为了解
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在很多书中给出的希尔排序的时间复杂度都不固定。在实际测试效果时,众多答案中,最符合的是O(N^1.3)。从这里就可以看出,希尔排序它非常的不稳。
总结
本篇文章主要介绍了希尔排序,希尔排序的时间复杂度与增量序列的选择有关,它是一种不稳定的排序算法,适用于中等规模的数据排序。希望本文对你有所帮助,最后,感谢阅读!
相关文章:

排序算法之【希尔排序】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...
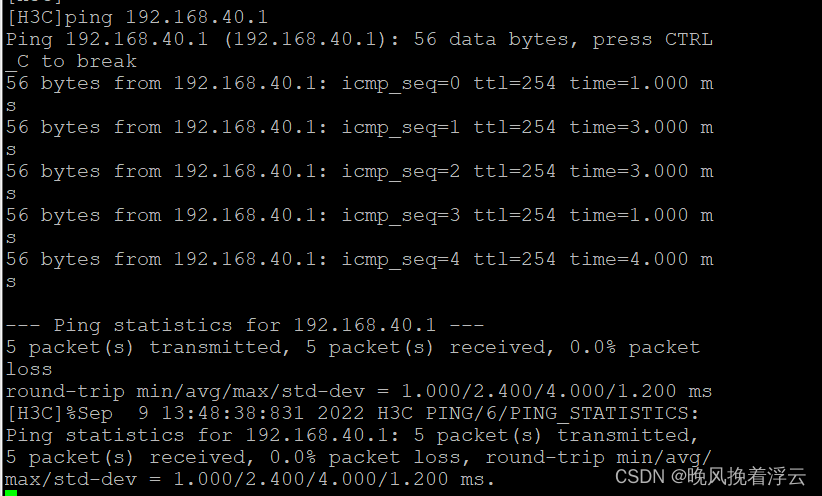
防火墙基础之H3C防火墙分支与分支之间双向地址转换
分支与分支之间双向地址转换 原理概述: 防火墙(英语:Firewall)技术是通过有机结合各类用于安全管理与筛选的软件和硬件设备,帮助计算机网络于其内、外网之间构建一道相对隔绝的保护屏障,以保护用户资…...
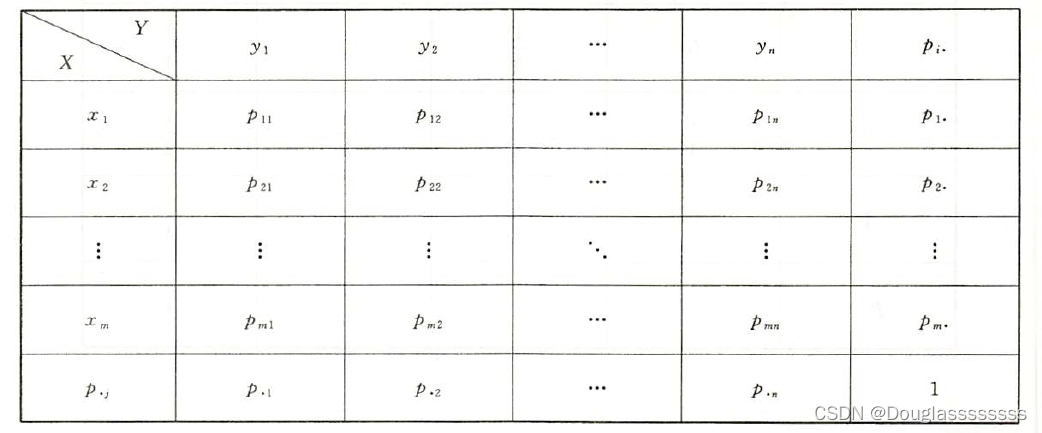
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(1,二维连续型和离散型随机变量基本概念与性质)
文章目录 引言一、二维随机变量及分布1.1 基本概念1.2 联合分布函数的性质 二、二维离散型随机变量及分布三、多维连续型随机变量及分布3.1 基本概念3.2 二维连续型随机变量的性质 写在最后 引言 隔了好长时间没看概率论了,上一篇文章还是 8.29 ,快一个…...

cesium 雷达扫描 (波纹线性雷达扫描效果)
cesium 雷达扫描 (波纹线性雷达扫描效果) 1、实现方法 使用ellipse方法加载圆型,修改ellipse中material方法来实现效果 2、示例代码 2.1 <!DOCTYPE html> <html lang="en"><head>&l...

SLAM从入门到精通(tf的使用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 在ros的机器人学习过程中,有一件事情是肯定少不了的。那就是坐标系的转换。其实这也很容易理解。假设有一个机器人,它有一个…...
python代码混淆与代码打包
0x00 背景 自己写的项目,又想保护源码,自己做个混淆是最方便的了。 0x01 实践 这里使用开源工具 GitHub - astrand/pyobfuscate: pyobfuscate,虽然git上才500多star,但是很好用。它的使用场景是混淆单个py文件。很多事物有开始就…...
)
Codeforces Round 899 (Div. 2)
Dashboard - Codeforces Round 899 (Div. 2) - Codeforces A. Increasing Sequence 由于a与b不相等,但b必须算出最小故可以从最小开始(1),故如果b a就将其值,使其改变即可,其余由于b1 < b2 < b3..…...

【 SuperPoint 】图像特征提取上的对比实验
1. SIFT,SuperPoint 都具有提取图片特征点,并且输出特征描述子的特性,本篇文章从特征点的提取数量,特征点的正确匹配数量来探索一下二者的优劣。 SuperPoint提取到的特征点数量要少一些,可以理解,我想原因大…...
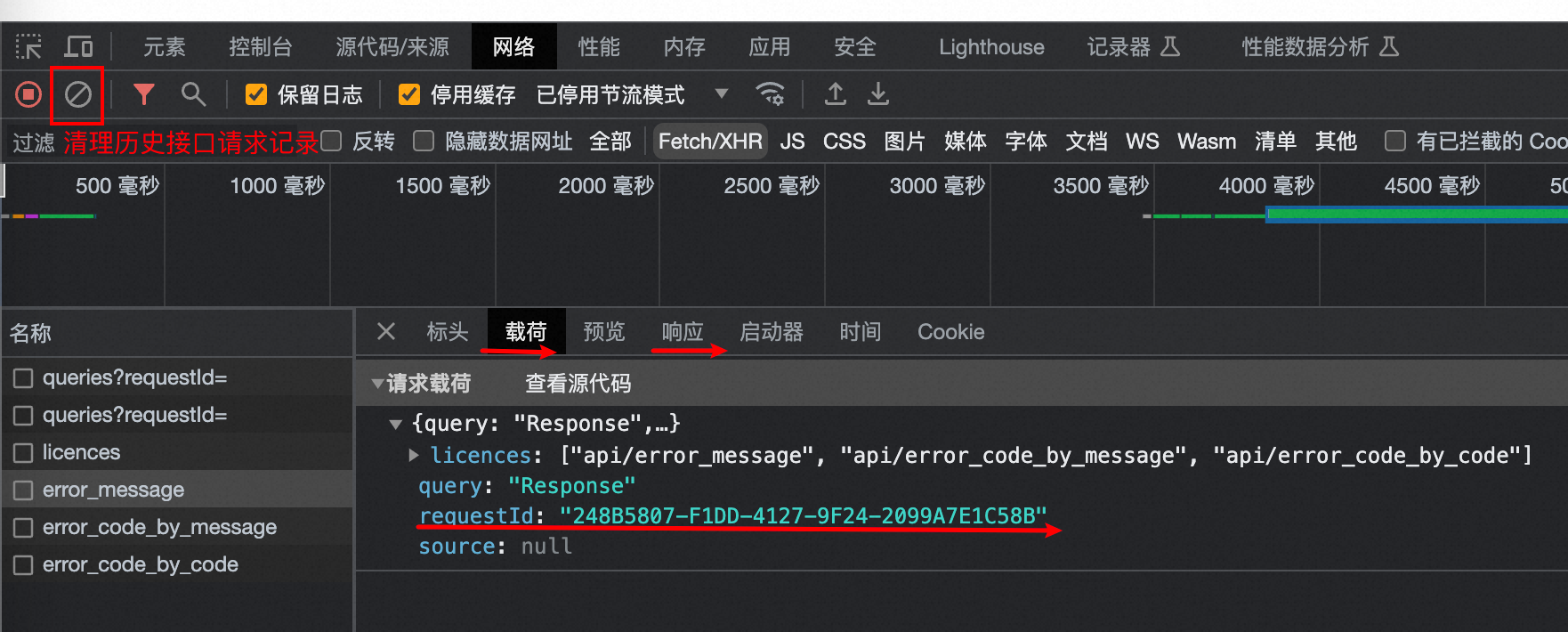
Chrome获取RequestId
Chrome获取RequestId 参考:https://help.aliyun.com/zh/redis/how-do-i-obtain-the-id-of-a-request 在浏览器页面按下F12键,打开开发者工具页面; 在开发者工具页面,单击Network(网络); 在playload(载荷)窗口中找到目…...

cesium 雷达扫描 (线行扩散效果)
cesium 雷达扫描 (线行扩散效果) 1、实现方法 使用ellipse方法加载圆型,修改ellipse中material方法来实现效果 2、示例代码 2.1、 <!DOCTYPE html> <html lang="en"><head><<...
【React】React组件生命周期以及触发顺序(部分与vue做比较)
最近在学习React,发现其中的生命周期跟Vue有一些共同点,但也有比较明显的区别,并且执行顺序也值得讨论一下,于是总结了一些资料在这里,作为学习记录。 v17.0.1后生命周期图片 初始化阶段 由ReactDOM.render()触发 —…...

【C++】多线程的学习笔记——白话文版(bushi
目录 为什么要使用多线程 例子 代码 结果 首先要先学的库——thread库 thread的简介 thread的具体使用方法 基本变量的定义 注意(小重点) join函数的解读(重点) detach函数的解读 注意 关于vector和thread是联合使用 …...
图像处理: ImageKit.NET 3.0.10704 Crack
关于 ImageKit.NET3 100% 原生 .NET 图像处理组件。 ImageKit.NET 可让您快速轻松地向 .NET 应用程序添加图像处理功能。从 TWAIN 扫描仪和数码相机检索图像;加载和保存多种格式的图像文件;对图像应用图像滤镜和变换;在显示屏、平移窗口或缩略…...
K8S内容分发网络之集群,nginx,负载均衡,防火墙
K8S内容分发网络之集群,nginx,负载均衡,防火墙 一、Kubernetes 区域可采用 Kubeadm 方式进行安装。1.所有节点,关闭防火墙规则,关闭selinux,关闭swap交换2.修改主机名3.所有节点修改hosts文件4.调整内核参数…...
不愧是疑问解决神器!你强任你强
不愧是疑问解决神器!你强任你强👍👍👍 在过去,我习惯用这种方式来阅读书籍或文章:先快速浏览一遍,然后再进行复读,并最终总结所学的知识点。然而,长期以来,我…...
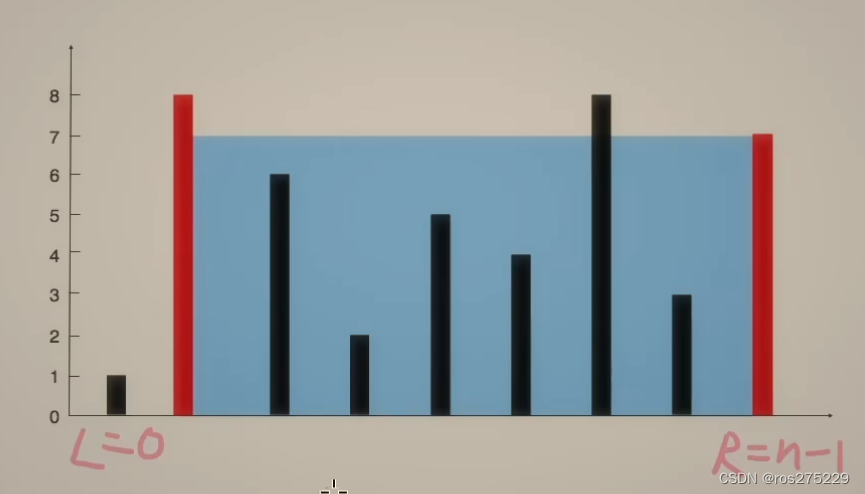
盛最多水的容器 接雨水【基础算法精讲 02】
盛雨水最多的容器 链接 : 11 盛最多水的容器 思路 : 双指针 : 1.对于两条确定的边界,l和r,取中间的线m与r组成容器,如果m的高度>l的高度,那么整个容器的长度会减小,如果低于l的高度,那么不仅高度可…...
之—— 主题的functions.php)
WordPress主题开发( 十二)之—— 主题的functions.php
WordPress主题开发( 十)之—— 主题的functions.php 介绍使用functions.php vs. 插件创建和使用functions.php在functions.php中的常见用途1. 使用WordPress钩子2. 启用WordPress功能3. 定义可重用的函数4. 添加自动Feed链接5. 自定义导航菜单6. 文本域加…...

代码的工厂模式
概念: 代码的工厂模式是一种设计模式,用于创建对象实例而无需直接调用构造函数。它提供了一种更加灵活和可维护的方式来创建对象,尤其是在需要根据不同情况创建不同类型的对象时非常有用。工厂模式隐藏了对象的创建细节,使代码更…...
UE5.1编辑器拓展【一、脚本化资产行为,通知,弹窗,高效复制多个同样的资产】
目录 插件制作 添加新的类:AssetActionUtility 添加新的模块:EditorScriptingUtilities 路径了解 添加debug的头文件 代码【debug.h】内涵注释: 写函数 .h文件 .cpp文件 插件制作 首先第一步是做一个插件:…...

mac openssl 版本到底怎么回事 已解决
在mac 安装node多版本的时候,有可能把原有的 openssl1.1 版本 直接要再一次升级了,无奈的 php环境 编译器是 openssl 1.1 还是 3.0 ,今天来个底朝天的找问题。 brew search openssl 有安装 三个版本。 但是错误提示 是第二个版本。 brew …...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
