BI神器Power Query(25)-- 使用PQ实现表格多列转换(1/3)
实例需求:原始表格包含多列属性数据,现在需要将不同属性分列展示在不同的行中,att1、att3、att5为一组,att2、att3、att6为另一组,数据如下所示。
更新表格数据
原始数据表:
| Col1 | Col2 | Att1 | Att2 | Att3 | Att4 | Att5 | Att6 |
|---|---|---|---|---|---|---|---|
| AAA | DDD | X | O | alpha | delta | 100 | 400 |
| BBB | EEE | Y | P | beta | vega | 200 | 500 |
结果数据表:
| Col1 | Col2 | cn1 | cn3 | cn3 |
|---|---|---|---|---|
| AAA | DDD | X | alpha | 100 |
| AAA | DDD | O | delta | 400 |
| BBB | EEE | Y | beta | 200 |
| BBB | EEE | P | vega | 500 |
示例代码:
letSource = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],add_index = Table.AddIndexColumn(Source, "Index", 1, 1, Int64.Type),tab1 = Table.RemoveColumns(add_index,{"Att2", "Att4", "Att6"}),rename_tab1 = Table.RenameColumns(tab1,{{"Att1", "cn1"}, {"Att3", "cn2"}, {"Att5", "cn3"}}),tab2 = Table.RemoveColumns(add_index,{"Att1", "Att3", "Att5"}),rename_tab2 = Table.RenameColumns(tab2,{{"Att2", "cn1"}, {"Att4", "cn2"}, {"Att6", "cn3"}}),combine_tab = Table.Combine({rename_tab1, rename_tab2}),sort_row = Table.Sort(combine_tab,{{"Index", Order.Ascending}}),output = Table.RemoveColumns(sort_row,{"Index"})
inoutput
代码解析:
第2行代码加载源表格,表格名称为Table1。
第3行代码添加索引列,用于确保输出结果表的数据顺序于原始表保持一致。
第4行代码移除多余列,保留部分属性列。
第5行代码重命名属性列名称。
第6~7行代码功能类似,用于提取第二组属性。
第8行代码合并两个子表。
第9行代码按索引列排序。
第1行代码移除索引列。
第12行代码输出最终结果表。
转换结果如下图所示。

部分代码也可以简化为如下,但是处理逻辑与上面代码相同,上述代码分步处理更容易理解。
letSource = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],add_index = Table.AddIndexColumn(Source, "Index", 1, 1, Int64.Type),combine_tab = Table.Combine({Table.RenameColumns(add_index[[Col1],[Col2],[Att1],[Att3],[Att5],[Index]],{{"Att1","cn1"},{"Att3","cn2"},{"Att5","cn3"}}),Table.RenameColumns(add_index[[Col1],[Col2],[Att2],[Att4],[Att6],[Index]],{{"Att2","cn1"},{"Att4","cn2"},{"Att6","cn3"}})}),sort_row = Table.Sort(combine_tab,{{"Index", Order.Ascending}}),output = Table.RemoveColumns(sort_row,{"Index"})
inoutput总结:
Power Query提供了丰富的表处理功能,可以方便地实现表格列的转换需求。
相关文章:

BI神器Power Query(25)-- 使用PQ实现表格多列转换(1/3)
实例需求:原始表格包含多列属性数据,现在需要将不同属性分列展示在不同的行中,att1、att3、att5为一组,att2、att3、att6为另一组,数据如下所示。 更新表格数据 原始数据表: Col1Col2Att1Att2Att3Att4Att5Att6AAADD…...
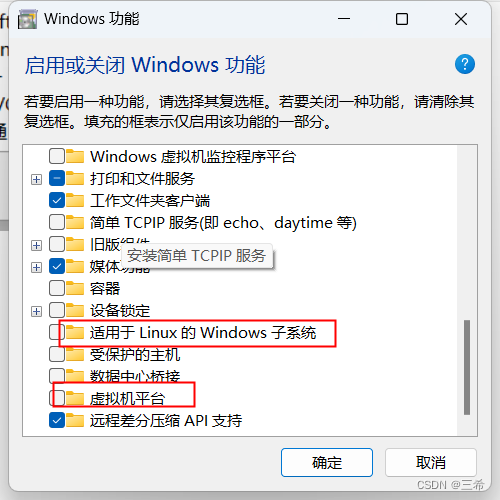
windows系统一键开启和关闭虚拟化
说明 跟虚拟化相关的三个程序 一键开启脚本 REM 开启 Hyper-V 服务 pushd "%~dp0"dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum >hyper-v.txtfor /f %%i in (findstr /i . hyper-v.txt 2^>nul) do dism /online /norestart /add-package:"%Sy…...

NSSCTF做题(5)
[NSSCTF 2022 Spring Recruit]babyphp 代码审计 if(isset($_POST[a])&&!preg_match(/[0-9]/,$_POST[a])&&intval($_POST[a])){ if(isset($_POST[b1])&&$_POST[b2]){ if($_POST[b1]!$_POST[b2]&&md5($_POST[b1])md5($_POST[b2])){…...

java基础题——二维数组的基本应用
1.设计程序按照各个学生的 Java 成绩进行排序 ( 降序 ) 2.设计程序,根据学生总成绩进行排序(降序排列),并输出学生姓名、每门课程的名称和该学生的成绩、该学生的总成绩 public static void main(String[] args) {String[] names {"安琪拉",…...

Leetcode 2119.反转两次的数字
反转 一个整数意味着倒置它的所有位。 例如,反转 2021 得到 1202 。反转 12300 得到 321 ,不保留前导零 。 给你一个整数 num ,反转 num 得到 reversed1 ,接着反转 reversed1 得到 reversed2 。如果 reversed2 等于 num &#x…...

BI神器Power Query(27)-- 使用PQ实现表格多列转换(3/3)
实例需求:原始表格包含多列属性数据,现在需要将不同属性分列展示在不同的行中,att1、att3、att5为一组,att2、att3、att6为另一组,数据如下所示。 更新表格数据 原始数据表: Col1Col2Att1Att2Att3Att4Att5Att6AAADD…...
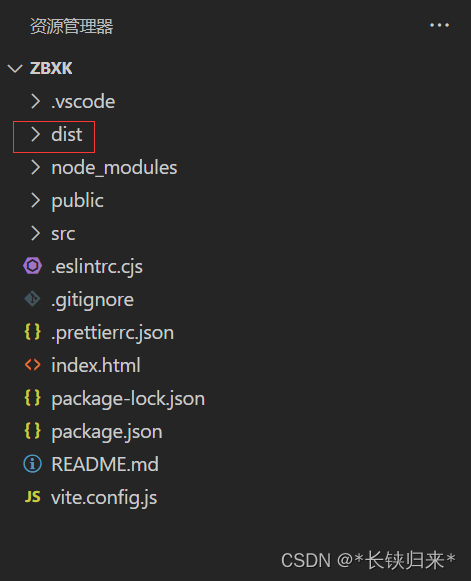
VUE3照本宣科——认识VUE3
VUE3照本宣科——认识VUE3 前言一、命令创建项目1.中文官网2.菜鸟教程 二、VUE3项目目录结构1.public2.src(1)assets(2)components 3. .eslintrc.cjs4. .gitignore5. .prettierrc.json6.index.html7.package.json8.README.md9.vit…...

《计算机视觉中的多视图几何》笔记(12)
12 Structure Computation 本章讲述如何在已知基本矩阵 F F F和两幅图像中若干对对应点 x ↔ x ′ x \leftrightarrow x x↔x′的情况下计算三维空间点 X X X的位置。 文章目录 12 Structure Computation12.1 Problem statement12.2 Linear triangulation methods12.3 Geomet…...

TFT LCD刷新原理及LCD时序参数总结(LCD时序,写的挺好)
cd工作原理目前不了解,日后会在博客中添加这一部分的内容。 1.LCD工作原理[1] 我对LCD的工作原理也仅仅处在了解的地步,下面基于NXP公司对LCD工作原理介绍的ppt来学习一下。 LCD(liquid crystal display,液晶显示屏) 是由液晶段阵列组成,当…...

基于Java的电影院购票系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

Linux基础指令(六)
目录 前言1. man 指令2. date 指令3. cal 指令4. bc 指令5. uname 指令结语: 前言 欢迎各位伙伴来到学习 Linux 指令的 第六天!!! 在上一篇文章 Linux基本指令(五) 中,我们通过一段故事线,带大家感性的了…...

Anderson-Darling正态性检验【重要统计工具】
Anderson-Darling正态性检验是一种用于确定数据集是否服从正态分布(也称为高斯分布或钟形曲线分布)的统计方法。它基于Anderson和Darling于1954年提出的检验统计量。该检验的基本原理和用途如下: 基本原理: 零假设(Nu…...
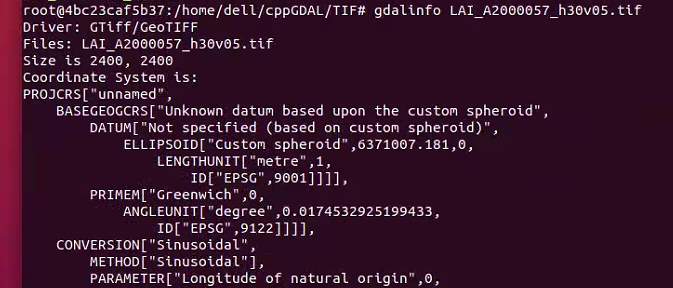
Ubuntu基于Docker快速配置GDAL的Python、C++环境
本文介绍在Linux的Ubuntu操作系统中,基于Docker快速配置Python、C等不同编程语言均可用的地理数据处理库GDAL的方法。 首先,我们访问GDAL库的Docker镜像官方网站(https://github.com/OSGeo/gdal/tree/master/docker)。其中&#x…...

<C++> 哈希表模拟实现STL_unordered_set/map
哈希表模板参数的控制 首先需要明确的是,unordered_set是K模型的容器,而unordered_map是KV模型的容器。 要想只用一份哈希表代码同时封装出K模型和KV模型的容器,我们必定要对哈希表的模板参数进行控制。 为了与原哈希表的模板参数进行区分…...

【数据结构与算法】通过双向链表和HashMap实现LRU缓存 详解
这个双向链表采用的是有伪头节点和伪尾节点的 与上一篇文章中单链表的实现不同,区别于在实例化这个链表时就初始化了的伪头节点和伪尾节点,并相互指向,在第一次添加节点时,不需要再考虑空指针指向问题了。 /*** 通过链表与HashMa…...
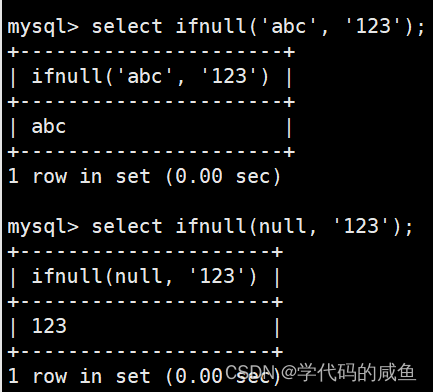
MySQL的内置函数
文章目录 1. 聚合函数2. group by子句的使用3. 日期函数4. 字符串函5. 数学函数6. 其它函数 1. 聚合函数 COUNT([DISTINCT] expr) 返回查询到的数据的数量 用SELECT COUNT(*) FROM students或者SELECT COUNT(1) FROM students也能查询总个数。 统计本次考试的数学成绩分数去…...

数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
)
Lilliefors正态性检验(一种非参数统计方法)
Lilliefors检验(也称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法,它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数…...
)
【云原生】配置Kubernetes CronJob自动备份MySQL数据库(单机版)
文章目录 每天自动备份数据库MySQL【云原生】配置Kubernetes CronJob自动备份Clickhouse数据库 每天自动备份数据库 MySQL 引用镜像:databack/mysql-backup,使用文档:https://hub.docker.com/r/databack/mysql-backup 测试、开发环境:每天0点40分执行全库备份操作,备份文…...
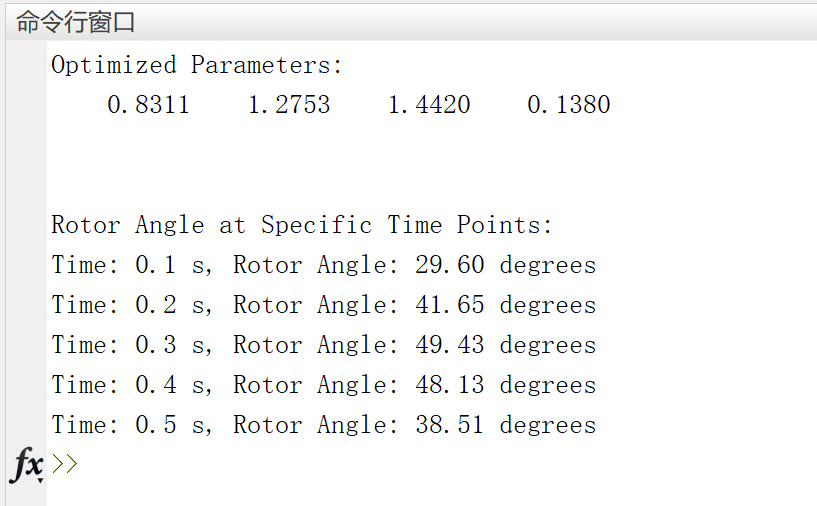
基于PSO算法的功率角摆动曲线优化研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
