Spring的注解开发-注解原理解析-xml方式/注解方式组件扫描
目录
Spring注解的解析原理
xml配置组件扫描
注解方式配置组件扫描
原理图
yysy,没有搞太明白,真的复杂,欢迎大佬留言解惑
Spring注解的解析原理
- 使用@Component等注解配置完毕后,要配置组件扫描才能使注解生效
-
xml配置组件扫描
-
<context:component-scan base-package="com.example"/> - 在往期文章中:Spring整合第三方框架_保持敬畏的博客-CSDN博客 ,我们了解同一标签中不同命名空间对应不同的解析器,对于上述中component-scan命名空间对应的解析器

-
ContextNamespaceHandler类

-
ComponentScanBeanDefinitionParser类
-
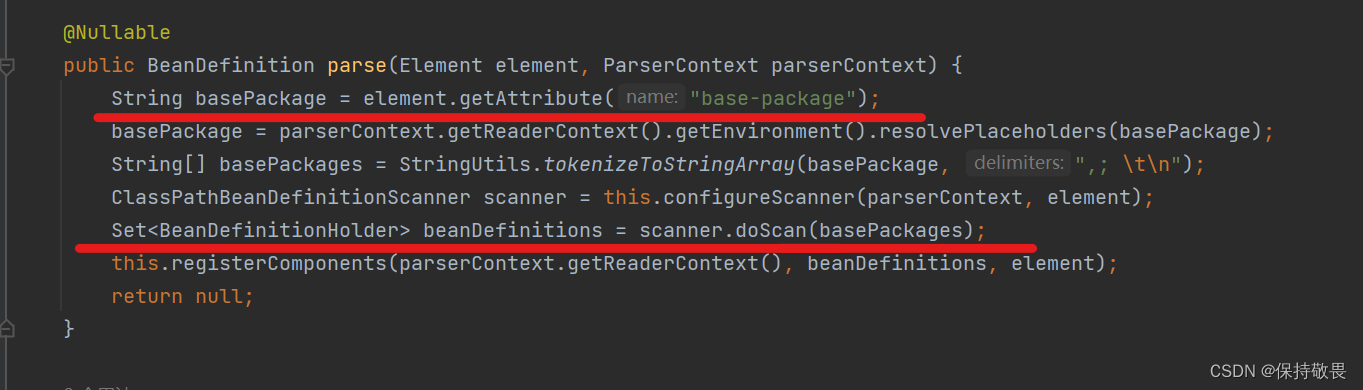
- doScan方法
- 在该方法中,对于添加了@Component注解及其衍生注解的类,为其创建BeanDefinition对象放入到BeanDefinitionMap中,然后就是经历SpringBean的生命周期,最后存入单例池中,被Spring容器管理。xml配置组件扫描该方法没有使用后处理器
-
-
-
注解方式配置组件扫描
-
@ComponentScan({"com.example"}) public class SpringConfig {} -
这中情况源码太复杂了,翻不下去了,大概是将BeanDefinitionRegisterPostProcessor注入到容器当中,再调用其中的doScan方法进行BeanDefinition注册。
-
-
原理图
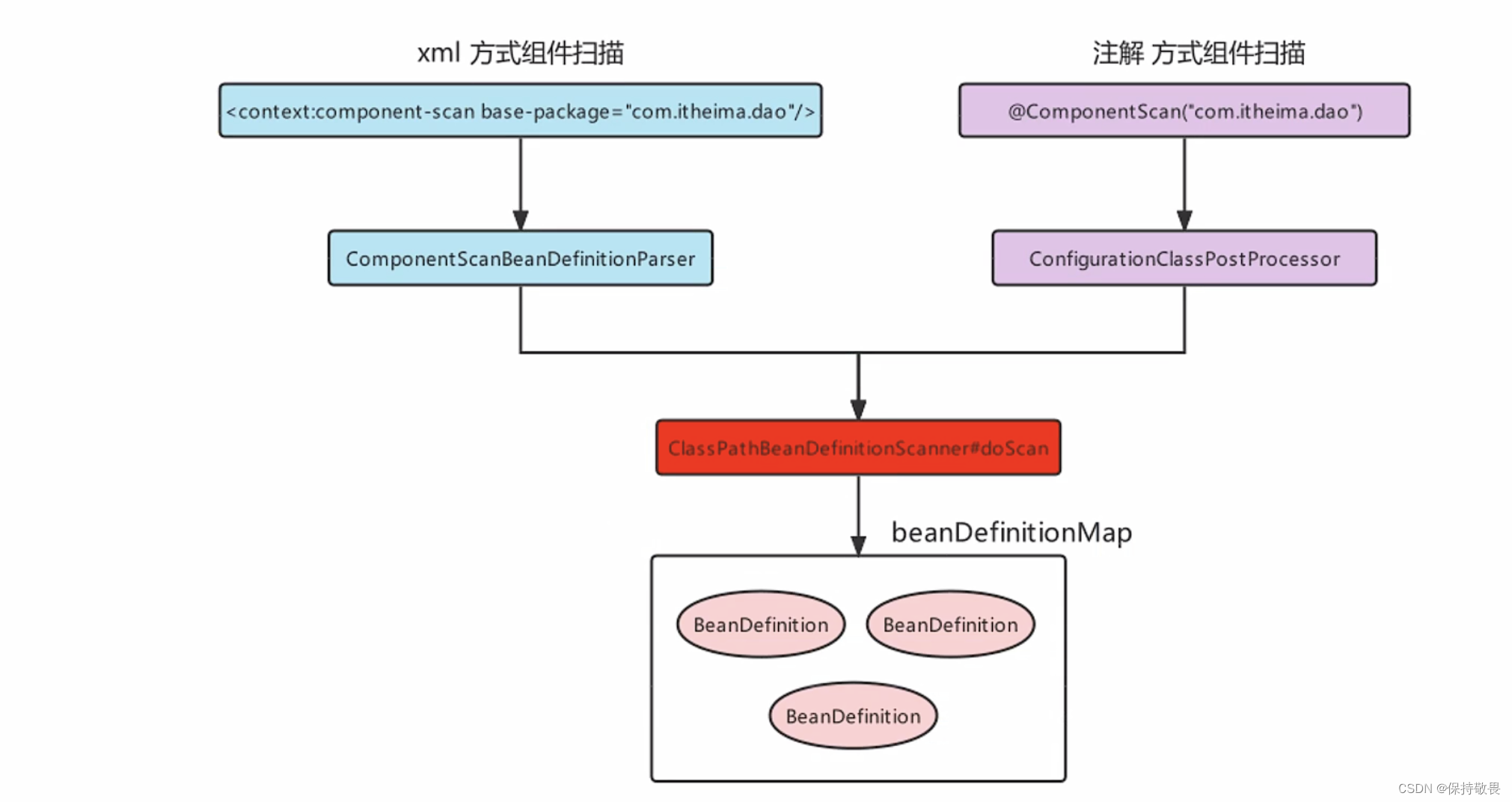
- xml方式:通过自定义标签的方式,通过ComponentScanBeanDefinitionParser解析最终通过调用Scanner的doScan方法进行beanDefiniton注册
- 注解方式:通过ConfigurationClassPostProcessor最终内部调用Scanner的doScan方法进行beanDefiniton注册
- 两种方式入口不同,但是最终核心代码解析component时代码是一样的。
-
yysy,没有搞太明白,真的复杂,欢迎大佬留言解惑
-
相关文章:

Spring的注解开发-注解原理解析-xml方式/注解方式组件扫描
目录 Spring注解的解析原理 xml配置组件扫描 注解方式配置组件扫描 原理图 yysy,没有搞太明白,真的复杂,欢迎大佬留言解惑 Spring注解的解析原理 使用Component等注解配置完毕后,要配置组件扫描才能使注解生效 xml配置组件扫…...
导出视频里的字幕
导出视频里的字幕 如何利用剪映快速提取并导出视频里的字幕 https://jingyan.baidu.com/article/c35dbcb0881b6fc817fcbcd2.html 如何快速提取视频中的字幕?给大家介绍一种简单高效又免费的提取方法。需要利用到“剪映”,以下是具体的操作步骤和指引&a…...

【KingbaseES】银河麒麟V10 ARM64架构_安装人大金仓数据库KingbaseES_V8R6(CentOS8)
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,Java基础学习,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的…...

【Vue】Vuex详解,一文读懂并使用Vuex
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《ELement》。🎯🎯 …...

第三章 C程序设计
常量与变量 常量:整型常量:如1000 实型常量:十进制小数 字符常量:?! 变量:变量必须先定义,后使用。 标识符:一个对象的名字。 浮点型数据 浮点型数据是用来表示具…...

QB/T 2703-2020 汽车装饰用皮革检测
汽车装饰用皮革主要用于坐垫皮革,座椅套皮革,靠垫套皮革,方向盘皮革和其他装饰用皮革,比如仪表盘等,其物理和环保性能非常重要,对人体的健康能起到很大的影响。 QB/T 5754-2022水性/无溶剂聚氨酯复合人造革…...

使用正则表达式批量修改函数
贪心匹配,替换中的$1代表括号中的第一组。 使用[\s\S\r]代表所有字符,同时加个问号代表不贪心匹配:...
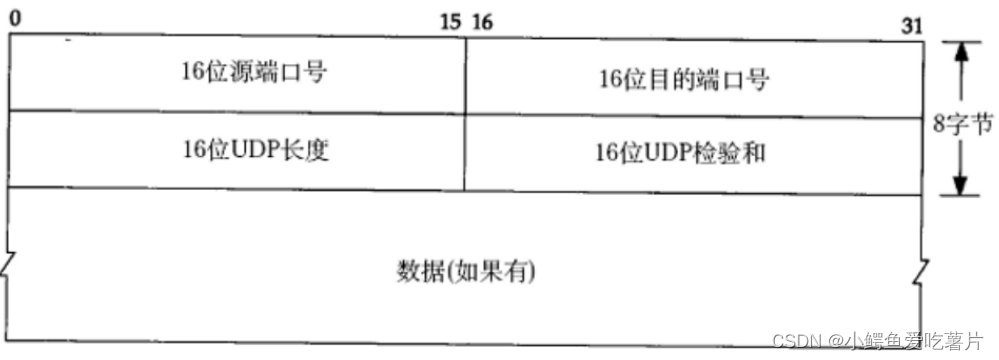
【网络协议】UDP
UDP协议与TCP协议都是传输层协议,应用层把数据拷贝到传输层,后续动作由下层自行决定。 UDP协议端格式 16位 UDP 长度 , 表示整个数据报 (UDP 首部 UDP 数据 ) 的最大长度 ;(也就是65535字节) 如果校验和出错 , 就会直接丢弃 ; …...
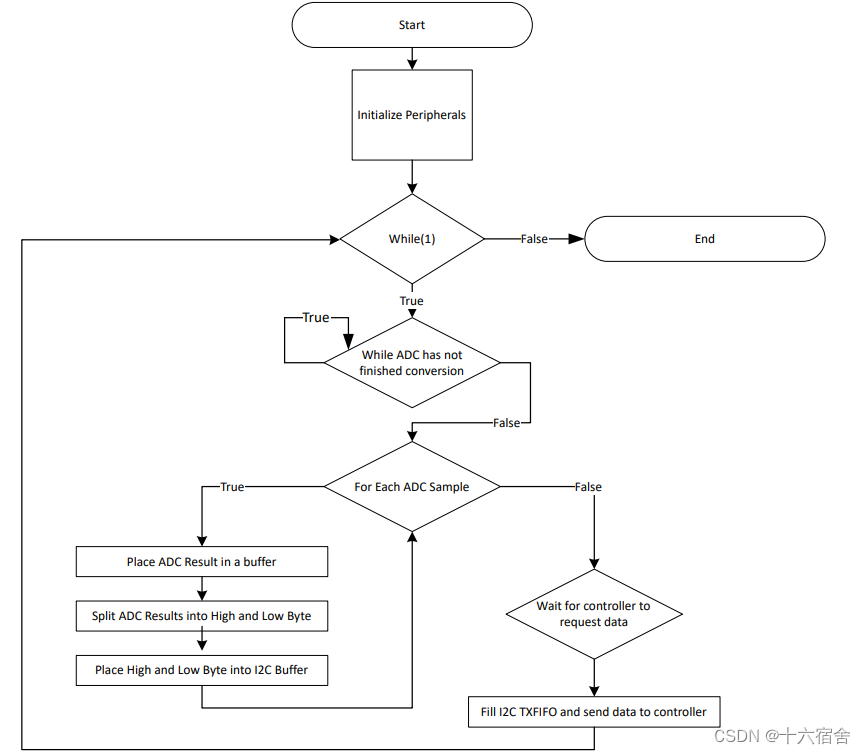
雷达编程实战之提高探测速度
有效帧频率作为雷达一个非常核心的指标,它代表了雷达探测识别的速度,速度越快,后级各项智能驾驶功能就能得到更快、更有效的判断。本篇文章首先从硬件的角度,提供了一种合理利用片上资源提高探测识别速度的常用方法,然…...

pyspark常用功能记录
前言 pyspark中很多常用的功能,过段时间没有使用就容易忘记,需要去网上搜索,这里总结一下,省的以后还去去搜,供自己以后参考。 withColumn def hot_func(info_str):if info_str:eturn "1"return "0&…...
Spring面试题学习: 单例Bean是单例模式吗?
单例Bean是单例模式吗 学习背景答案扩展知识单例模式Spring BeanJava Bean单例Bean 个人评价我的回答 学习背景 想换工作. 学习记录, 算是一个输出. 答案 通常来说, 单例模式是指在一个JVM中, 一个类只能构造出一个对象. 有很多方法来实现单例模式, 比如饿汉模式. 但是我们通…...
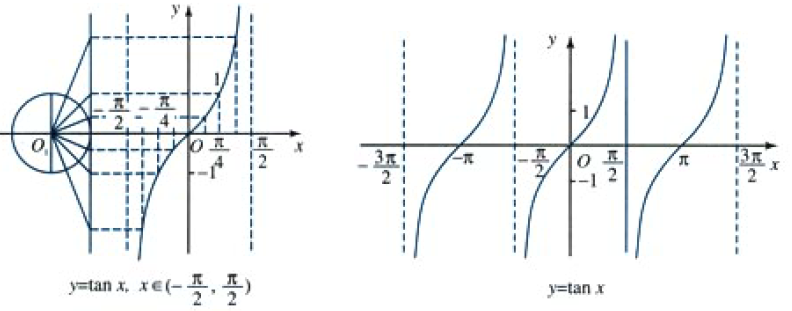
EM@常用三角函数图象性质(中学部分)
文章目录 abstract正弦函数正弦型函数转动相关概念旋转角速度转动周期转动频率初相小结 余弦函数的图象与性质性质 正切函数的图象和性质由已知三角函数值求角任意角范围内反三角函数(限定范围内)反正弦反余弦反正切 abstract 讨论 sin , cos , tan \sin,\cos,\tan s…...
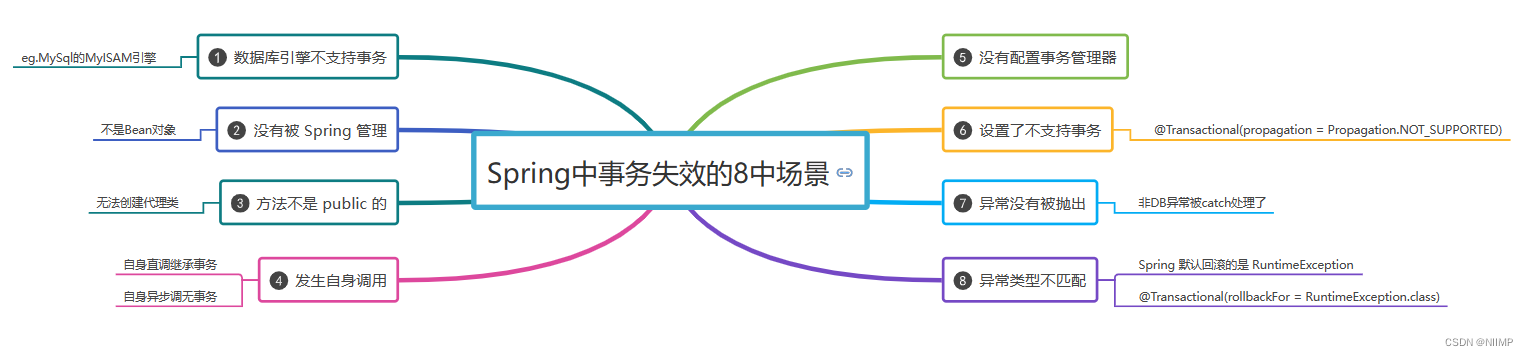
一文拿捏Spring事务之、ACID、隔离级别、失效场景
1.🌟Spring事务 1.编程式事务 事务管理代码嵌入嵌入到业务代码中,来控制事务的提交和回滚,例如TransactionManager 2.声明式事务 使用aop对方法前后进行拦截,然后在目标方法开始之前创建或者加入一个事务,执行完目…...
input输入表头保存excel文件
input输入表头 input输入表头 (input内除了/,空格 回车 标点符号等 全部作为单元格分隔符)保存/storage/emulated/0/代码文件/ 没有就创建文件名命名方法:编号. 库 时间戳嗨!听说你有个需求,想根据用户输入…...

DataBinding双向绑定简介
一、简介 在Vue中使用的是MVVM架构。通过ViewModel可以实现M层和V层数据的双向绑定。Model层的数据发生变化后,会自动更新View层UI。UI层数据发生变化(用户输入),可以驱动Model层的数据发生变化,借助于Vue框架中的View…...
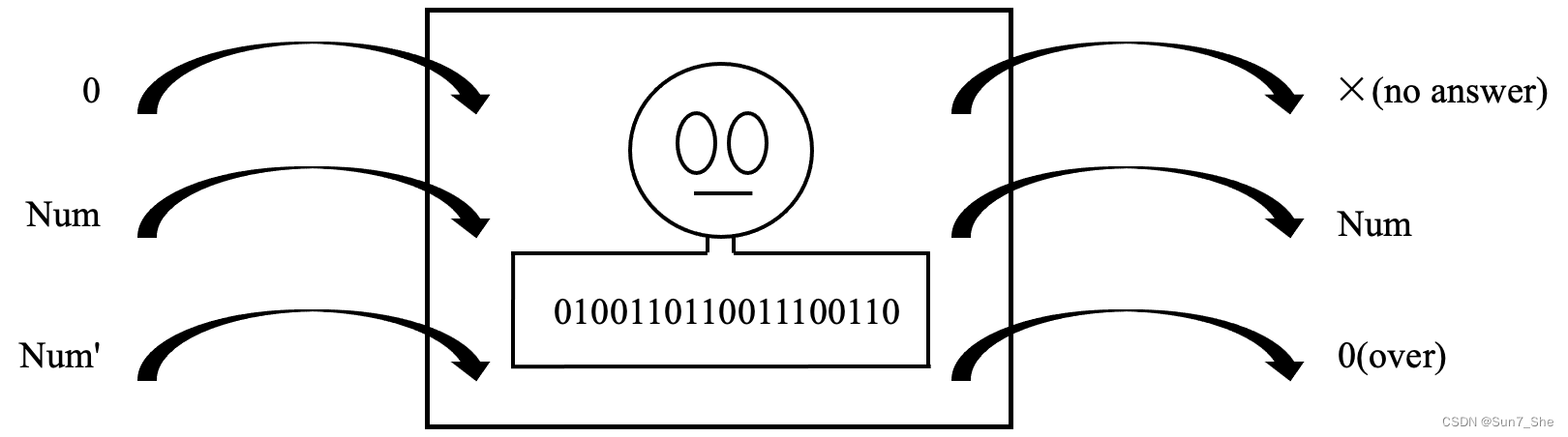
Is This The Intelligent Model(这是智能模型吗)
Is This The Intelligent Model 这是智能模型吗 Ruoqi Sun Academy of Military Science Defense Innovation Institute, Beijing, 100091, China E-mail: ruoqisun7163.com The exposed models are called artificial intelligent models[1-3]. These models rely on knowled…...

MySQL事务:特性、使用、并发事务问题和隔离级别
什么是事务? 在数据库中,事务是一组SQL操作,它们被视为一个单一的工作单元。事务必须同时成功或失败,以确保数据库的一致性。事务通常遵循ACID属性,即原子性(Atomicity)、一致性(Co…...

FFmpeg日志系统、文件与目录、操作目录
目录 FFmpeg日志系统 FFmpeg文件与目录操作 FFmpeg文件的删除与重命名 FFmpeg操作目录及list的实现 操作目录重要函数 操作目录重要结构体 FFmpeg日志系统 下面看一个简单的 demo。 #include <stdio.h> #include <libavutil/log.h>int main(int argc,char* …...

好奇喵 | Surface Web ---> Deep Web ---> Dark Web
前言 我们可能听说过深网(deep Web)、暗网(dark Web)等名词,有些时候可能会认为它们是一个东西,其实不然,两者的区别还是比较大的。 什么是deep web? 深网是网络的一部分,与之相对应的是表层网络(surface …...
三、thymeleaf基本语法
3.1、基本语法 3.1.1变量表达式:${...} 变量表达式用于在页面中输出指定的内容,此内容可以是变量,可以是集合的元素,也可以是对象的属性。主要用于填充标签的属性值,标签内的文本,以及页面中js变量的值等…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

