EM@常用三角函数图象性质(中学部分)
文章目录
- abstract
- 正弦函数
- 正弦型函数
- 转动相关概念
- 旋转角速度
- 转动周期
- 转动频率
- 初相
- 小结
- 余弦函数的图象与性质
- 性质
- 正切函数的图象和性质
- 由已知三角函数值求角
- 任意角范围内
- 反三角函数(限定范围内)
- 反正弦
- 反余弦
- 反正切
abstract
- 讨论 sin , cos , tan \sin,\cos,\tan sin,cos,tan的图象性质,这些性质可以借助单位圆分析
- y = cos x y=\cos{x} y=cosx:余弦曲线
- y = sin x y=\sin{x} y=sinx:正弦曲线
- y = tan x y=\tan{x} y=tanx:正切曲线
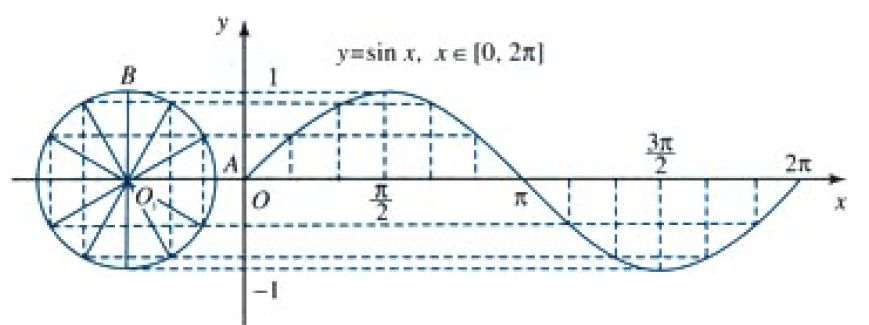 | 正弦线和正弦曲线 |
|---|---|
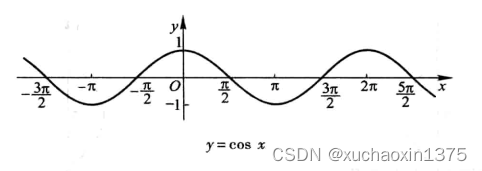 | 余弦曲线 |
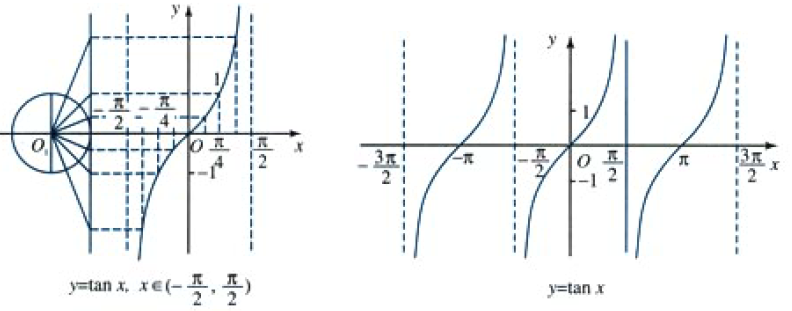 | 正切线和正切曲线 |
正弦函数
- y = sin x y=\sin{x} y=sinx, x ∈ R x\in\mathbb{R} x∈R是正弦函数,其中自变量 x x x是弧度值
- 定义域: R \mathbb{R} R
- 值域: [ − 1 , 1 ] [-1,1] [−1,1]
- 当 x = − π 2 + 2 k π x=-\frac{\pi}{2}+2k\pi x=−2π+2kπ, k ∈ Z k\in\mathbb{Z} k∈Z时取得最小值 − 1 -1 −1
- 当 x = π 2 + 2 k π x=\frac{\pi}{2}+2k\pi x=2π+2kπ, k ∈ Z k\in\mathbb{Z} k∈Z时取得最大值1
- 有界性: ∣ sin x ∣ ⩽ 1 |\sin{x}|\leqslant{1} ∣sinx∣⩽1
- 奇偶性:奇函数
- 周期性:最小正周期为 2 π 2\pi 2π
- 单调性: [ − π 2 + 2 k π , π 2 + 2 k π ] [-\frac{\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi] [−2π+2kπ,2π+2kπ]为递增区间; [ π 2 + 2 k π , 3 π 2 + 2 k π ] [\frac{\pi}{2}+2k\pi,\frac{3\pi}{2}+2k\pi] [2π+2kπ,23π+2kπ]为递减区间; k ∈ Z k\in\mathbb{Z} k∈Z
- 正弦函数刻画的是弧度 x x x对应的正弦值 sin x \sin{x} sinx
正弦型函数
- y = A sin ( ω x + ϕ ) y=A\sin(\omega{x}+\phi) y=Asin(ωx+ϕ),称为正弦型函数
- 相比于正弦函数 y = sin x y=\sin{x} y=sinx, y = A sin ( ω x + ϕ ) y=A\sin(\omega{x}+\phi) y=Asin(ωx+ϕ)增加了两个影响函数的参数 A , ω , ϕ A,\omega,\phi A,ω,ϕ(它们不是变量,而都是常数)
- 这个函数在物理应用中很常见,具有明显的物理意义
- 正弦型函数和仍可以用圆周运动来描述:
- 设直角坐标系中某点 P ( x , y ) P(x,y) P(x,y)绕着原点 O O O以半径为 R R R的圆轨迹作角速度为 ω \omega ω rad/s的圆周运动
- 设旋转前 P P P的位置为 P 0 P_0 P0,且 O P OP OP是 ϕ \phi ϕ的终边
- 经过 t t t秒后,点 P P P来到了新位置,且 O P OP OP是 ϕ + ω t \phi+\omega{t} ϕ+ωt的终边
- 容易算得 P P P的坐标 ( x , y ) (x,y) (x,y)关于时间 t t t的函数关系
- x = R cos ( ω t + ϕ ) x=R\cos(\omega{t}+\phi) x=Rcos(ωt+ϕ)
- y = R sin ( ω t + ϕ ) y=R\sin(\omega{t}+\phi) y=Rsin(ωt+ϕ)
- 推导方式如下:
- 在直角坐标系 x O y xOy xOy上,令角 ϕ \phi ϕ的顶点为 O O O坐标原点重合, ϕ \phi ϕ的始边与 x x x轴正半轴重合
- 并以 O O O为圆心构造单位圆, ϕ \phi ϕ与单位圆的交点的坐标为 E ( cos ϕ , sin ϕ ) E(\cos\phi,\sin{\phi}) E(cosϕ,sinϕ)
- 而 P 0 P_0 P0也是 ϕ \phi ϕ终边上的点,且 O P 0 = R OP_0=R OP0=R;则 P 0 P_0 P0的坐标 ( P 0 x , P 0 y ) (P_{0x},P_{0y}) (P0x,P0y)是 E E E的坐标 ( sin α , cos α ) (\sin\alpha,\cos\alpha) (sinα,cosα)的 R R R倍: P 0 x = R cos ϕ P_{0x}=R\cos\phi P0x=Rcosϕ, P 0 y = R sin ϕ P_{0y}=R\sin\phi P0y=Rsinϕ
- 对于终边 ω t + ϕ \omega{t}+\phi ωt+ϕ上的 P P P点坐标为 ( R cos ( ω t + ϕ ) , R sin ( ω t + ϕ ) ) (R\cos(\omega{t}+\phi),R\sin(\omega{t}+\phi)) (Rcos(ωt+ϕ),Rsin(ωt+ϕ))
- 这就得到了正弦型函数 y = A sin ( ω x + ϕ ) y=A\sin(\omega{x}+\phi) y=Asin(ωx+ϕ)
转动相关概念
旋转角速度
- 坐标系内的点 P ( x , y ) P(x,y) P(x,y)绕点 O O O在单位时间内旋转过的角的弧度数 ω \omega ω
转动周期
-
y = R sin ( ω t + ϕ ) y=R\sin(\omega{t}+\phi) y=Rsin(ωt+ϕ)中,点 P P P旋转一周所需要的时间为 T = 2 π ω T=\frac{2\pi}{\omega} T=ω2π,这个时间也称为转动周期
- 令 α = ω t + ϕ \alpha=\omega{t}+\phi α=ωt+ϕ,设函数 y y y的最小正周期为 T 0 T_0 T0,则 y ( t + T 0 ) y(t+T_0) y(t+T0)= y ( t ) y(t) y(t)
- 即 R sin ( ω ( t + T 0 ) + ϕ ) R\sin(\omega{(t+T_0)}+\phi) Rsin(ω(t+T0)+ϕ)= R sin ( ω t + ϕ ) R\sin(\omega{t}+\phi) Rsin(ωt+ϕ),即 sin ( ( ω t + ϕ ) + ω T 0 ) \sin((\omega{t}+\phi)+\omega T_0) sin((ωt+ϕ)+ωT0)= sin ( ω t + ϕ ) \sin(\omega{t}+\phi) sin(ωt+ϕ)
- 所以 sin ( α + T 0 ) = sin ( α ) \sin(\alpha+T_0)=\sin(\alpha) sin(α+T0)=sin(α)
- sin α \sin\alpha sinα的周期为 2 π 2\pi 2π,那么 ω T 0 \omega{T_0} ωT0= 2 π 2\pi 2π,所以 T 0 = 2 π ω T_{0}=\frac{2\pi}{\omega} T0=ω2π
-
此外,还可以从坐标的伸缩角度来得到转动周期计算公式
-
例: sin ( k x ) \sin(kx) sin(kx), k = 1 , 2 , 3 , ⋯ , n k=1,2,3,\cdots,n k=1,2,3,⋯,n时,在 [ 0 , 2 π ] [0,2\pi] [0,2π]内取得最大值1的极值点(满足 k x = π 2 kx=\frac{\pi}{2} kx=2π)分别是: π 2 \frac{\pi}{2} 2π, π 4 \frac{\pi}{4} 4π, π 6 \frac{\pi}{6} 6π, ⋯ \cdots ⋯, π 2 n \frac{\pi}{2n} 2nπ
转动频率
- 一秒内,点 P P P旋转的周数 f = 1 T f=\frac{1}{T} f=T1= ω 2 π \frac{\omega}{2\pi} 2πω,称为转动的频率
初相
- 角 ϕ \phi ϕ也叫做初相
小结
- 转动周期(转动频率)只和 ω \omega ω相关,而与 ϕ \phi ϕ无关
- ω \omega ω越大,在一定区间内曲线波动的次数就越多,反之越少
余弦函数的图象与性质
- 我们可以通过诱导公式 y = sin ( π 2 + x ) y=\sin(\frac{\pi}{2}+x) y=sin(2π+x)= cos x \cos{x} cosx得知, y = cos x y=\cos{x} y=cosx的图象和 sin ( π 2 + x ) \sin(\frac{\pi}{2}+x) sin(2π+x)的图象相同
- 所以可以通过研究正弦型函数来研究余弦函数(正弦函数向左平移2个单位就可以得到余弦函数的图象)
- 此外,余弦型函数 y = A cos ( ω x + ϕ ) y=A\cos(\omega{x}+\phi) y=Acos(ωx+ϕ)可以转换为 y = A sin ( ω x + ϕ + π 2 ) y=A\sin(\omega{x}+\phi+\frac{\pi}{2}) y=Asin(ωx+ϕ+2π)
性质
- 定义域和值域和周期同正弦函数
- 当且仅当 x = π + 2 k π x=\pi+2k\pi x=π+2kπ, k ∈ Z k\in\mathbb{Z} k∈Z时,取得最小值 − 1 -1 −1
- 当且仅当 x = 2 k π x=2k\pi x=2kπ, k ∈ Z k\in\mathbb{Z} k∈Z时,余弦函数取值得最大值1
- 奇偶性:偶函数
- 单调性: [ 2 k π , π + 2 k π ] [2k\pi,\pi+2k\pi] [2kπ,π+2kπ], k ∈ Z k\in\mathbb{Z} k∈Z时函数单调递减; [ π + 2 k π , 2 π + 2 k π ] [\pi+2k\pi,2\pi+2k\pi] [π+2kπ,2π+2kπ], k ∈ Z k\in\mathbb{Z} k∈Z函数单调递增
正切函数的图象和性质
- 定义域: { x ∣ x ≠ k π + π 2 , k ∈ Z } \set{x|x\neq{k\pi+\frac{\pi}{2}},k\in\mathbb{Z}} {x∣x=kπ+2π,k∈Z},
- 值域: R \mathbb{R} R
- 在区间 ( − π 2 , π 2 ) (-\frac{\pi}{2},\frac{\pi}{2}) (−2π,2π)内,当 x < π 2 x<\frac{\pi}{2} x<2π且无限接近 π 2 \frac{\pi}{2} 2π时, tan x \tan{x} tanx趋于无限大,记为 tan x → + ∞ \tan{x}\to{+\infin} tanx→+∞
- 另一侧有 x → − π 2 x\to{-\frac{\pi}{2}} x→−2π时 tan x → − ∞ \tan{x}\to{-\infin} tanx→−∞
- 周期: π \pi π
- 由 tan ( π + x ) \tan(\pi+x) tan(π+x)= tan x \tan{x} tanx,所以 π \pi π是 tan x \tan{x} tanx的一个周期
- 并且结合单位圆中的正弦线,容易说明最小正周期为 π \pi π
- 奇偶性:奇函数
- 单调性: ( − π 2 + k π , π 2 + k π ) (-\frac{\pi}{2}+k\pi,\frac{\pi}{2}+k\pi) (−2π+kπ,2π+kπ), k ∈ Z k\in\mathbb{Z} k∈Z区间内函数单调增加
由已知三角函数值求角
任意角范围内
- 通常可以用单位圆来求解具有给定三角函数值对应的弧度角
- 例如:已知 sin x = 2 2 \sin{x}=\frac{\sqrt{2}}{2} sinx=22,求
- x x x的可能取值
- x ∈ [ − π 2 , π 2 ] x\in[-\frac{\pi}{2},\frac{\pi}{2}] x∈[−2π,2π]条件下 x x x的取值
- 解:
- 由单位圆可知, π 4 + 2 k π \frac{\pi}{4}+2k\pi 4π+2kπ, ( π − π 4 ) + 2 k π (\pi-\frac{\pi}{4})+2k\pi (π−4π)+2kπ, ( k ∈ Z ) (k\in\mathbb{Z}) (k∈Z)都满足 sin x = 2 2 \sin{x}=\frac{\sqrt{2}}{2} sinx=22,
- 用集合表示为: { x ∣ x = 2 k π + π 4 ( k ∈ Z ) } \set{x|x=2k\pi+\frac{\pi}{4}(k\in{\mathbb{Z}})} {x∣x=2kπ+4π(k∈Z)} ⋃ \bigcup ⋃ { x ∣ x = 2 k π + 3 π 4 ( k ∈ Z ) } \set{x|x=2k\pi+\frac{3\pi}{4}(k\in\mathbb{Z})} {x∣x=2kπ+43π(k∈Z)}
- 若 x ∈ [ − π 2 , π 2 ] x\in[-\frac{\pi}{2},\frac{\pi}{2}] x∈[−2π,2π],由单位圆可知, x = π 4 x=\frac{\pi}{4} x=4π
- 由单位圆可知, π 4 + 2 k π \frac{\pi}{4}+2k\pi 4π+2kπ, ( π − π 4 ) + 2 k π (\pi-\frac{\pi}{4})+2k\pi (π−4π)+2kπ, ( k ∈ Z ) (k\in\mathbb{Z}) (k∈Z)都满足 sin x = 2 2 \sin{x}=\frac{\sqrt{2}}{2} sinx=22,
反三角函数(限定范围内)
- 已知三角函数值求角的过程的所建立的函数称为反三角函数
- 由于单射函数才有反函数,反三角函数根据限定三角函数内的一段单调区间定义出来
反正弦
- 一般地,对于正弦函数 y = sin x y=\sin{x} y=sinx,若已知函数值为 y ( y ∈ [ − 1 , 1 ] ) y(y\in[-1,1]) y(y∈[−1,1]),那么 [ − π 2 , π 2 ] [-\frac{\pi}{2},\frac{\pi}{2}] [−2π,2π]上由唯一的 x x x值和它对应,记为 x = arcsin y x=\arcsin{y} x=arcsiny,(其中 − 1 ⩽ y ⩽ 1 -1\leqslant{y}\leqslant{1} −1⩽y⩽1, − π 2 ⩽ x ⩽ π 2 -\frac{\pi}{2}\leqslant{x}\leqslant{\frac{\pi}{2}} −2π⩽x⩽2π)
- 例如: sin x = 1 2 \sin{x}=\frac{1}{2} sinx=21, x ∈ [ − π 2 , π 2 ] x\in[-\frac{\pi}{2},\frac{\pi}{2}] x∈[−2π,2π],求 x x x的问题可以表示为 arcsin 1 2 \arcsin{\frac{1}{2}} arcsin21
反余弦
- 在区间 [ 0 , π ] [0,\pi] [0,π]上符合条件 cos x = y \cos{x}=y cosx=y, ( y ∈ [ − 1 , 1 ] ) (y\in[-1,1]) (y∈[−1,1])的求角 x x x,记为 x = arccos y x=\arccos{y} x=arccosy
- 例
- arccos 1 2 = π 3 \arccos{\frac{1}{2}}=\frac{\pi}{3} arccos21=3π
- 已知 cos x = − 2 2 \cos{x}=-\frac{\sqrt{2}}{2} cosx=−22,且 x ∈ [ 0 , 2 π ] x\in[0,2\pi] x∈[0,2π],求 x x x的取值集合
- 由单位圆可知,解集为 { 3 π 4 , 5 π 4 } \set{\frac{3\pi}{4},\frac{5\pi}{4}} {43π,45π}
- 用反余弦函数表示: { arccos ( − 2 2 ) , π + arccos 2 2 } \set{\arccos{(-\frac{\sqrt{2}}{2})},\pi+\arccos\frac{\sqrt{2}}{2}} {arccos(−22),π+arccos22}
反正切
- 一般地,若 tan x = y ( y ∈ R ) \tan{x}=y(y\in\mathbb{R}) tanx=y(y∈R),且 x ∈ ( − π 2 , π 2 ) x\in(-\frac{\pi}{2},\frac{\pi}{2}) x∈(−2π,2π),那么对每一个正切值 y y y,在开区间 ( − π 2 , π 2 ) (-\frac{\pi}{2},\frac{\pi}{2}) (−2π,2π)内,有且只有一个角 x x x满足 tan x = y \tan{x}=y tanx=y,记为 x = arctan y x=\arctan{y} x=arctany, x ∈ ( − π 2 , π 2 ) x\in(-\frac{\pi}{2},\frac{\pi}{2}) x∈(−2π,2π)
- 例如 arctan 3 3 \arctan{\frac{\sqrt{3}}{3}} arctan33= π 6 \frac{\pi}{6} 6π
相关文章:

EM@常用三角函数图象性质(中学部分)
文章目录 abstract正弦函数正弦型函数转动相关概念旋转角速度转动周期转动频率初相小结 余弦函数的图象与性质性质 正切函数的图象和性质由已知三角函数值求角任意角范围内反三角函数(限定范围内)反正弦反余弦反正切 abstract 讨论 sin , cos , tan \sin,\cos,\tan s…...
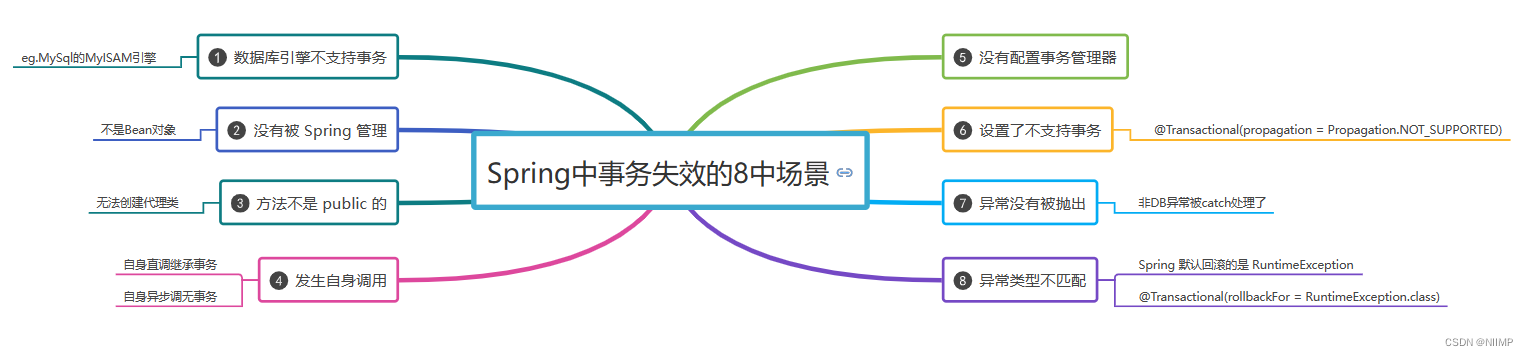
一文拿捏Spring事务之、ACID、隔离级别、失效场景
1.🌟Spring事务 1.编程式事务 事务管理代码嵌入嵌入到业务代码中,来控制事务的提交和回滚,例如TransactionManager 2.声明式事务 使用aop对方法前后进行拦截,然后在目标方法开始之前创建或者加入一个事务,执行完目…...
input输入表头保存excel文件
input输入表头 input输入表头 (input内除了/,空格 回车 标点符号等 全部作为单元格分隔符)保存/storage/emulated/0/代码文件/ 没有就创建文件名命名方法:编号. 库 时间戳嗨!听说你有个需求,想根据用户输入…...

DataBinding双向绑定简介
一、简介 在Vue中使用的是MVVM架构。通过ViewModel可以实现M层和V层数据的双向绑定。Model层的数据发生变化后,会自动更新View层UI。UI层数据发生变化(用户输入),可以驱动Model层的数据发生变化,借助于Vue框架中的View…...
Is This The Intelligent Model(这是智能模型吗)
Is This The Intelligent Model 这是智能模型吗 Ruoqi Sun Academy of Military Science Defense Innovation Institute, Beijing, 100091, China E-mail: ruoqisun7163.com The exposed models are called artificial intelligent models[1-3]. These models rely on knowled…...

MySQL事务:特性、使用、并发事务问题和隔离级别
什么是事务? 在数据库中,事务是一组SQL操作,它们被视为一个单一的工作单元。事务必须同时成功或失败,以确保数据库的一致性。事务通常遵循ACID属性,即原子性(Atomicity)、一致性(Co…...

FFmpeg日志系统、文件与目录、操作目录
目录 FFmpeg日志系统 FFmpeg文件与目录操作 FFmpeg文件的删除与重命名 FFmpeg操作目录及list的实现 操作目录重要函数 操作目录重要结构体 FFmpeg日志系统 下面看一个简单的 demo。 #include <stdio.h> #include <libavutil/log.h>int main(int argc,char* …...

好奇喵 | Surface Web ---> Deep Web ---> Dark Web
前言 我们可能听说过深网(deep Web)、暗网(dark Web)等名词,有些时候可能会认为它们是一个东西,其实不然,两者的区别还是比较大的。 什么是deep web? 深网是网络的一部分,与之相对应的是表层网络(surface …...
三、thymeleaf基本语法
3.1、基本语法 3.1.1变量表达式:${...} 变量表达式用于在页面中输出指定的内容,此内容可以是变量,可以是集合的元素,也可以是对象的属性。主要用于填充标签的属性值,标签内的文本,以及页面中js变量的值等…...

创建一个新的IDEA插件项目
启动IntelliJ IDEA并按照以下步骤创建新的插件项目: 打开IntelliJ IDEA并单击“Create New Project”(创建新项目)。 在左侧菜单栏中选择“IntelliJ Platform Plugin”(IntelliJ平台插件)。 在右侧窗格中,…...

Doris数据库BE——冷热数据方案
新的冷热数据方案是在整合了存算分离模型的基础上建立的,其核心思路是:DORIS本地存储作为热数据的载体,而外部集群(HDFS、S3等)作为冷数据的载体。数据在导入的过程中,先作为热数据存在,存储于B…...
Python无废话-办公自动化Excel格式美化
设置字体 在使用openpyxl 处理excel 设置格式,需要导入Font类,设置Font初始化参数,常见参数如下: 关键字参数 数据类型 描述 name 字符串 字体名称,如Calibri或Times New Roman size 整型 大小点数 bold …...

竞赛 机器视觉的试卷批改系统 - opencv python 视觉识别
文章目录 0 简介1 项目背景2 项目目的3 系统设计3.1 目标对象3.2 系统架构3.3 软件设计方案 4 图像预处理4.1 灰度二值化4.2 形态学处理4.3 算式提取4.4 倾斜校正4.5 字符分割 5 字符识别5.1 支持向量机原理5.2 基于SVM的字符识别5.3 SVM算法实现 6 算法测试7 系统实现8 最后 0…...
)
Django 数据库迁移(Django-04)
一 数据库迁移 数据库迁移是一种数据库管理技术,它用于在应用程序的开发过程中,根据模型(Model)的变化自动更新数据库结构,以保持数据库与代码模型的一致性。数据库迁移的主要目的是确保数据库与应用程序的模型定义同…...

Redis相关概念
1. 什么是Redis?它主要用来什么的? Redis,英文全称是Remote Dictionary Server(远程字典服务),是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提…...
Scala第十八章节
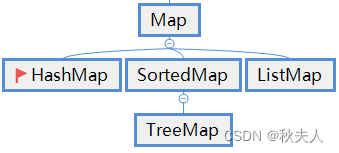
Scala第十八章节 scala总目录 文档资料下载 章节目标 掌握Iterable集合相关内容.掌握Seq集合相关内容.掌握Set集合相关内容.掌握Map集合相关内容.掌握统计字符个数案例. 1. Iterable 1.1 概述 Iterable代表一个可以迭代的集合, 它继承了Traversable特质, 同时也是其他集合…...

JAVA学习(4)-全网最详细~
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
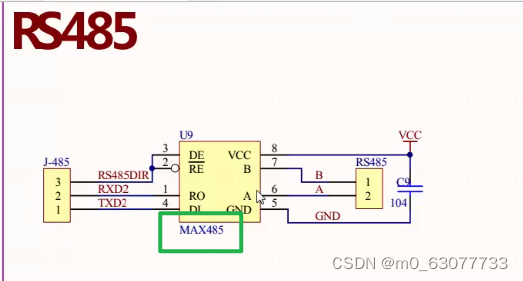
【单片机】12-串口通信和RS485
1.通信有关的常见概念 区分:串口,COM口,UART,USART_usart和串口区别-CSDN博客 串口、COM口、UART口, TTL、RS-232、RS-485区别详解-CSDN博客 1.什么是通信 (1)人和人之间的通信:说话ÿ…...

一步步教你使用GDB调试程序:从入门到精通的全面指南
文章目录 Step1:安装GDB1.1、包管理器安装1.2、下载源码编译安装 Step2:编译程序时添加调试信息Step3:GDB启动、退出、查看代码Step4:GDB断点操作Step5:GDB调试操作5.1 单步调试5.2 多进程调试 调试是软件开发中非常重…...
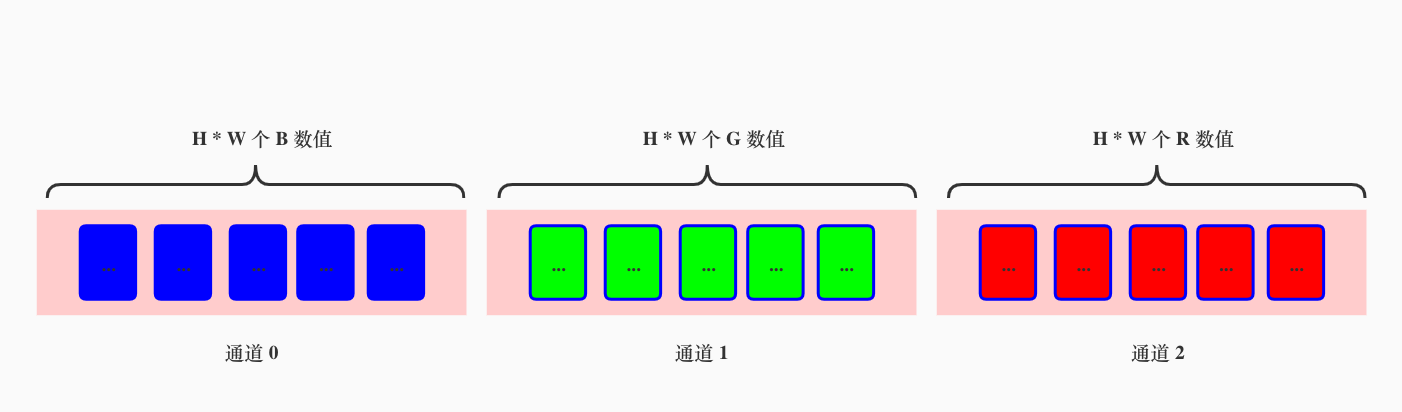
OpenCV读取图像时按照BGR的顺序HWC排列,PyTorch按照RGB的顺序CHW排列
OpenCV读取RGB图像 在OpenCV中,读取的图片默认是HWC格式,即按照高度、宽度和通道数的顺序排列图像尺寸的格式。我们看最后一个维度是C,因此最小颗粒度是C。 例如,一张形状为2562563的RGB图像,在OpenCV中读取后的格式…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
