深入剖析红黑树:优雅地平衡二叉搜索树

目录
- 一.红黑树的概念
- 二.插入操作
- 三.与AVL树的比较
一.红黑树的概念
在之前的学习中,我们了解了二叉搜索平衡树,AVL树通过控制每个结点中的平衡因子的绝对值不超过1,实现了一个高性能的树。而相较于AVL的高度平衡,红黑树觉得AVL为了平衡也付出了代价(插入和删除时进行了多次旋转),所以红黑树在控制平衡上面没有这么严格,只是要求,最长路径不超过最短路径的二倍。那红黑树又是如何控制实现的呢?接下来了解一下红黑树的性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的(任何路径上没有连续两个红结点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也称为NIL结点)
二.插入操作
在我们了解红黑树的性质后,就需要分析相关代码看他如何实现的。首先我们看红黑树结点的定义:
因为map和set的底层使用红黑树实现了,为了之后方便,这里红黑树用了两个模板参数。
#include <iostream>using namespace std;enum Colour
{RED, BLACK
};template<class K,class V>
class RBTreeNode
{
public:RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};
结点定义中与AVL树差距不大,只是多了个用枚举定义的参数,用来指定是红结点还是黑结点。接下来讲解重点的插入操作:
首先因为红黑树也是二叉搜索树,所以要满足二叉搜索树的基本性质,再者是我们插入的结点的颜色先置为什么能让后面的调整更方便呢。如果黑色需要在后面依据性质4调整,插入红色的话依据性质3调整。明显是4更为复杂,所以我们插入颜色为红色。
bool Insert(const pair<K, V>& kv)
{if(_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;///开始调整颜色///开始调整颜色_root->_col = BLACK;return true;
}
上段代码是不涉及调整颜色,只保证二叉搜索树性质。下面开始分类讨论研究如何调整颜色。
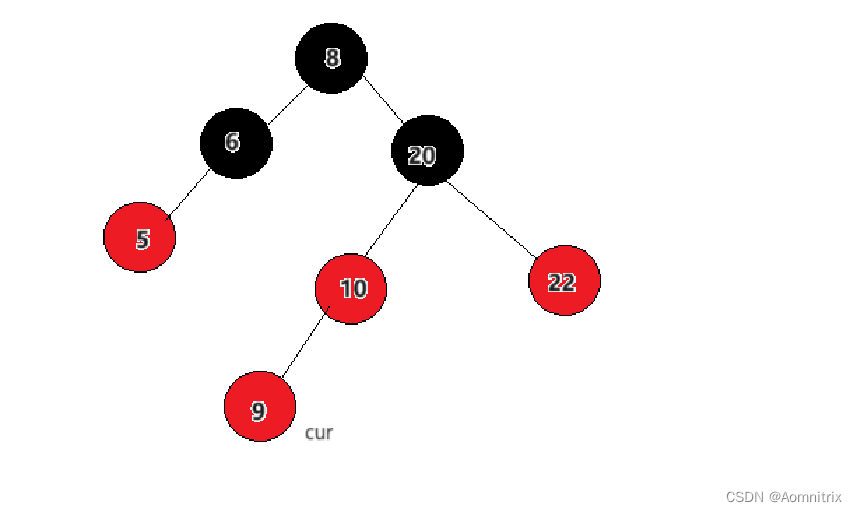
如上图所示,插入的cur结点是红色,这时出现了连续的两个红结点,所以就要进行调整。如果parent结点是黑色则不需要调整。我们把10结点和20结点称为parent和grandfather结点,22为uncle结点。
1.当uncle结点为红色时,变色然后继续向上调整
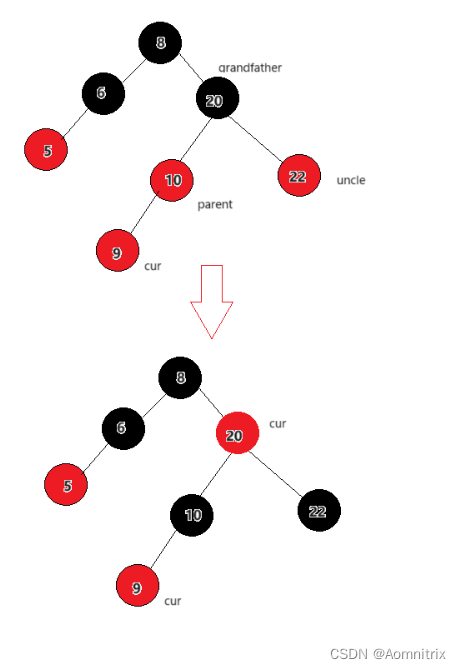
2.当uncle结点不存在时或者为黑时的处理方式相同:
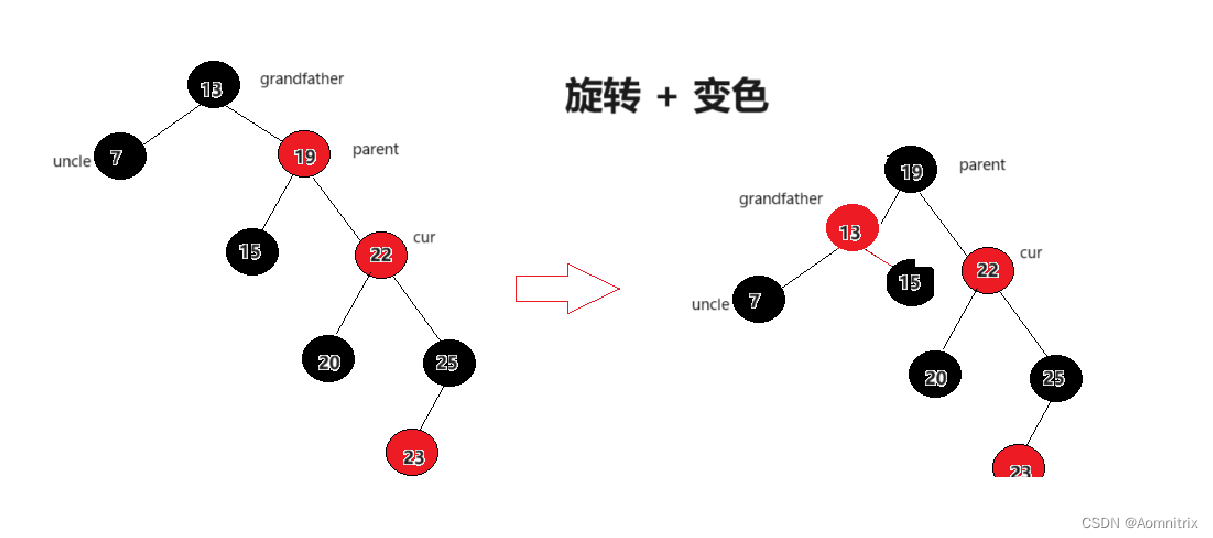
完整代码如下:
bool Insert(const pair<K, V>& kv){if(_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else // 叔叔不存在或者为黑都是旋转+变色{if (cur == parent->_left){RevoR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RevoL(parent);RevoR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}}}else{Node* uncle = grandfather->_left;//叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else // 叔叔不存在或者为黑都是旋转+变色{if (cur == parent->_left){RevoR(parent);RevoL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}else{RevoL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true;}void RevoL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;//无论curleft是否为空都要执行这一步if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RevoR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright){curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (_root == parent)//等价于 ppnode == nullptr{_root = cur;cur->_parent = nullptr;}else{cur->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}}}
三.与AVL树的比较
红黑树和AVL树的插入效率O(logN),只是红黑树不像AVL追求如此平衡,所以旋转次数会少,并且实现也较简单。所以在实践中大都使用红黑树。之后我们还是使用红黑树模拟实现map和set。
相关文章:

深入剖析红黑树:优雅地平衡二叉搜索树
目录 一.红黑树的概念二.插入操作三.与AVL树的比较 一.红黑树的概念 在之前的学习中,我们了解了二叉搜索平衡树,AVL树通过控制每个结点中的平衡因子的绝对值不超过1,实现了一个高性能的树。而相较于AVL的高度平衡,红黑树觉得AVL为…...
C10K问题:高并发模型设计
一、循环服务器模型 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <errno.h> #include <unistd.h> #include <signal.h> #include <sys/types.h> #include <sys/socket.h> //*******// #include &l…...

哈希/散列--哈希表[思想到结构][==修订版==]
文章目录 1.何为哈希?1.1百度搜索1.2自身理解1.3哈希方法/散列方法1.4哈希冲突/哈希碰撞1.5如何解决?哈希函数的设计 2.闭散列和开散列2.1闭散列/开放定址法2.2开散列/链地址法/开链法1.概念2.容量问题3.字符串问题4.开散列性能测试5.开散列与闭散列比较 3.代码实现[配备详细…...

成都建筑模板批发市场在哪?
成都作为中国西南地区的重要城市,建筑业蓬勃发展,建筑模板作为建筑施工的重要材料之一,在成都也有着广泛的需求。如果您正在寻找成都的建筑模板批发市场,广西贵港市能强优品木业有限公司是一家值得关注的供应商。广西贵港市能强优…...

亨元模式 结构型模式之六
1.定义 享元模式是一种结构型设计模式, 它允许你在消耗少量内存的情况下支持大量对象。 2.滑滑梯问题 在说明亨元模式之前,我们先看看关于滑滑梯的程序设计。小区的楼下只有三个滑滑梯,但是想玩的小朋友却非常多。怎么设计计滑滑梯资源的管理…...

面试题: Spring中Bean的实例化和Bean的初始化有什么区别?
Spring中Bean的实例化和Bean的初始化有什么区别? 背景答案扩展知识什么是实例化什么是初始化 个人评价我的回答 背景 想换工作, 看了图灵周瑜老师的视频想记录一下, 算是学习结果的一个输出. 答案 Spring 在创建一个Bean对象时, 会先创建出一个Java对象, 会通过反射来执行…...

阻塞队列,生产者消费者模型
目标: 1. 认识与使用阻塞队列 2. 认识与实现消费者模型 目录 阻塞队列的特点 生产者消费者模型 生产者消费者模型的优点 阻塞队列实现该模型 阻塞队列的特点 1. 线程安全 2. 带有阻塞特性 (1)如果队列为空,继续出队列&a…...

【RCRL充放电时间相关计算】
一. 基础知识 L、C元件称为“惯性元件”,即电感中的电流、电容器两端的电压,都有一定的“电惯性”,不能突然变化。充放电时间,不光与L、C的容量有关,还与充/放电电路中的电阻R有关。RC电路的时间常数:τRC…...

C++ primer plus--输入、输出和文件
17 输入、输出和文件 17.1 C 输入和输出概述 C 把输入和输出看做字节流。输入时,程序从输入流中抽取字节;输出时,程序将字节插到输出流中。 缓冲区是内存中的临时存储区域,是程序与文件或其他 I/O 设备之间的桥梁。 17.2 使用…...

案例题--Web应用考点
案例题--Web应用考点 负载均衡技术微服务XML和JSON无状态和有状态真题 在选择题中没有考察过web的相关知识,主要就是在案例分析题中考察 负载均衡技术 应用层负载均衡技术 传输层负载均衡技术 就近的找到距离最近的服务器,并进行分发 使用户就近获取…...

MySQL的SQL 优化:提升数据库性能
1. 插入操作优化 1.1 使用多值插入 通常情况下,插入大量数据时,使用多值插入语句比逐行插入更高效。例如,将多个数据行打包成一个 INSERT 语句: INSERT INTO users (name, email) VALUES (Alice, aliceexample.com), (Bob, bob…...
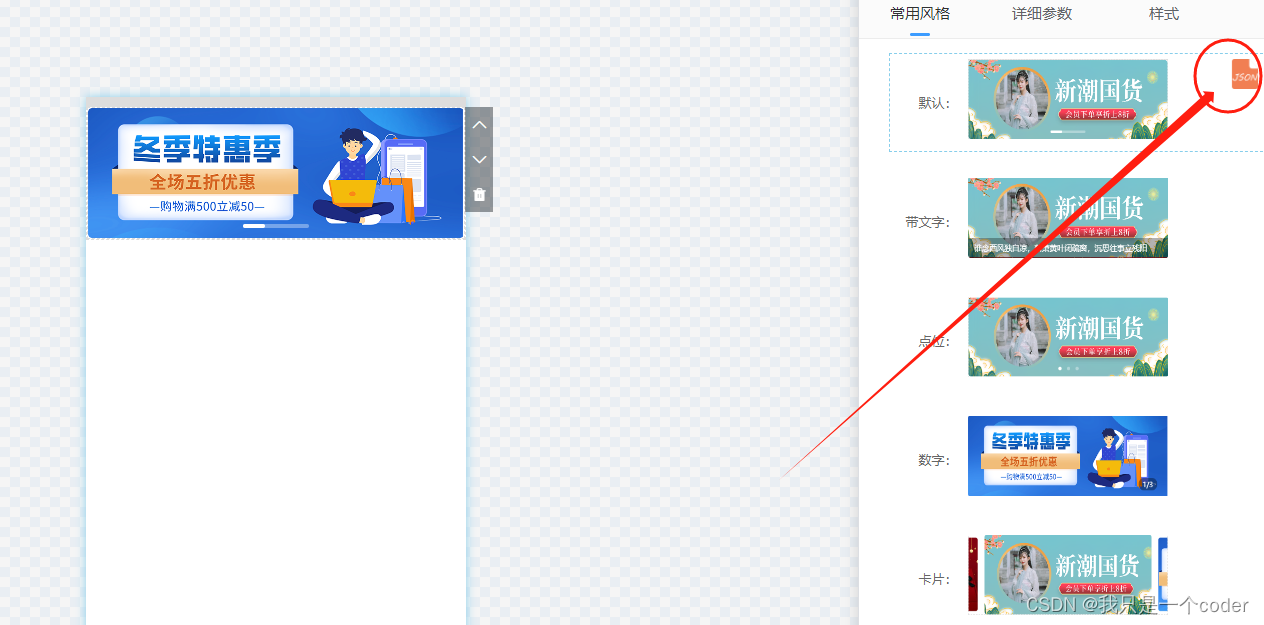
【匠心打造】从0打造uniapp 可视化拖拽设计 c_o 第十篇
一、click one for uniapp置顶: 全部免费开源 (你商业用途也没关系,不过可以告诉我公司名或者项目名,放在官网上好看点。哈哈-_-) 二、写在之前 距离上一篇更新已经大约4个月了,公司的事情,自己的一些琐事一直没时间…...

BIT-5-操作符详解(C语言初阶学习)
1. 各种操作符的介绍。 2. 表达式求值 1. 操作符分类: 算术操作符 移位操作符 位操作符 赋值操作符 单目操作符 关系操作符 逻辑操作符 条件操作符 逗号表达式 下标引用、函数调用和结构成员 2. 算术操作符 - * / % 除了 % 操作符…...
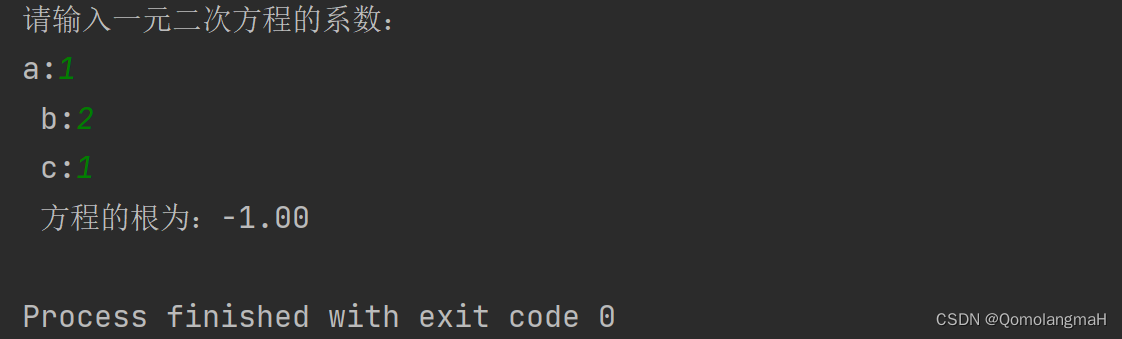
【重拾C语言】三、分支程序设计(双分支和单分支程序设计、逻辑判断、多分支程序设计、枚举类型表示;典型例题:判断闰年和求一元二次方程根)
目录 前言 三、分支程序设计 3.1 判断成绩是否及格——双分支程序设计 3.2 成绩加上获奖信息—单分支程序设计 3.3 逻辑判断——布尔类型 3.4 获奖分等级——多分支程序设计 3.5 表示汽车种类——枚举类型 3.6 例题 3.6.1 例题——判断某个年份是否闰年 3.6.2 例题—…...

Shiro应用到Web Application
一、权限基础 a) 认证(你是谁?) 判断你(被认证者)是谁的过程。通常被认证者提供用户名和密码。 常见的认证包含如下几种: 匿名认证:允许访问资源,不做任何类型的安全检查。表单认证:访问资源之前,需要提…...

【POST请求-腾讯翻译君-爬虫案例】
原因:尝试多个在线翻译平台,由于返回数据存在加密原因(暂时不会解密),最总找到 ”腾讯翻译君“ 完成爬虫案例POST请求测试 案例测试网址 腾讯翻译 :https://fanyi.qq.com/ import requests import jsoncla…...

多卡片效果悬停效果
效果展示 页面结构 从页面的结构上看,在默认状态下毛玻璃卡片是有层次感的效果叠加在一起,并且鼠标悬停在卡片区域后,卡片整齐排列。 CSS3 知识点 transform 属性的 rotate 值运用content 属性的 attr 值运用 实现页面整体布局 <div …...
首饰饰品经营商城小程序的作用是什么
首饰如耳钉、戒指、手镯等除了高价值产品外,还有很多低价产品,市场需求客户众多,在实际经营中,商家们也会面临一些痛点。 私域话题越来越多加之线上线下同行竞争、流量匮乏等,更对商家选择自建商城经营平台。 通过【…...

华为OD机试真题【服务器能耗统计】
1、题目描述 【服务器能耗统计】 服务器有三种运行状态:空载、单任务、多任务,每个时间片的能耗的分别为1、3、4; 每个任务由起始时间片和结束时间片定义运行时间; 如果一个时间片只有一个任务需要执行,则服务器处于单任务状志; 如果一个时间片有多个任务需要执行,则服务器处于…...
)
ubuntu按下del却出现空格(命令行下键盘错乱)
问题: 有一天远程我的ubuntu 20.04,发现为何按 del 会产生空格后移的效果,up键也会重叠显示,首先感觉是这个远程软件有问题,于是又换了xshell,发现还是不行,只能打开积灰已久的笔记本࿰…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
