约束优化算法(optimtool.constrain)
import optimtool as oo
from optimtool.base import np, sp, plt
pip install optimtool>=2.4.2
约束优化算法(optimtool.constrain)
import optimtool.constrain as oc
oc.[方法名].[函数名]([目标函数], [参数表], [等式约束表], [不等式约数表], [初始迭代点])
import optimtool.constrain as oc
f, x1, x2 = sp.symbols("f x1 x2")
f = (x1 - 2)**2 + (x2 - 1)**2
c1 = x1 - x2 - 1
c2 = 0.25*x1**2 - x2 - 1
等式约束(equal)
oc.equal.[函数名]([目标函数], [参数表], [等式约束表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| penalty_quadratice(funcs: FuncArray, args: FuncArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=10, p: float=2, epsk: float=1e-4, epsilon: float=1e-4, k: int=0) -> OutputType | 增加二次罚项 |
| lagrange_augmentede(funcs: FuncArray, args: ArgArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, lamk: float=6, sigma: float=10, p: float=2, etak: float=1e-4, epsilon: float=1e-6, k: int=0) -> OutputType | 增广拉格朗日乘子法 |
oc.equal.penalty_quadratice(f, (x1, x2), c1, (1, 0.5), verbose=True)
(1, 0.5) 1.25 0
[2. 1.] 4.930380657631324e-32 1
(1.9999999999999998, 1.0) 4.930380657631324e-32 2
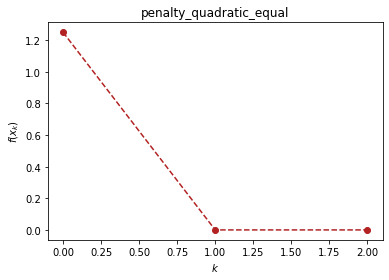
((1.9999999999999998, 1.0), 2)
不等式约束(unequal)
oc.unequal.[函数名]([目标函数], [参数表], [不等式约束表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| penalty_quadraticu(funcs: FuncArray, args: ArgArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=10, p: float=0.4, epsk: float=1e-4, epsilon: float=1e-10, k: int=0) -> OutputType | 增加二次罚项 |
| lagrange_augmentedu(funcs: FuncArray, args: ArgArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, muk: float=10, sigma: float=8, alpha: float=0.2, beta: float=0.7, p: float=2, eta: float=1e-1, epsilon: float=1e-4, k: int=0) -> OutputType | 增广拉格朗日乘子法 |
oc.unequal.lagrange_augmentedu(f, (x1, x2), c2, (1.5, 0.5), verbose=True)
(1.5, 0.5) 0.5 0
(1.5, 0.5) 0.5 1
[2. 1.] 0.0 2
(2.0, 1.0) 0.0 3
(2.0, 1.0) 0.0 4
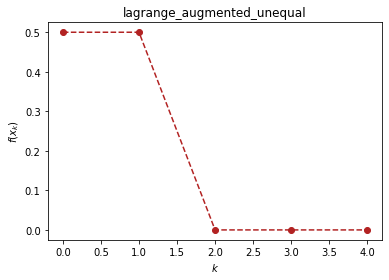
((2.0, 1.0), 4)
混合等式约束(mixequal)
oc.mixequal.[函数名]([目标函数], [参数表], [等式约束表], [不等式约束表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| penalty_quadraticm(funcs: FuncArray, args: ArgArray, cons_equal: FuncArray, cons_unequal: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=10, p: float=0.6, epsk: float=1e-6, epsilon: float=1e-10, k: int=0) -> OutputType | 增加二次罚项 |
| penalty_L1(funcs: FuncArray, args: ArgArray, cons_equal: FuncArray, cons_unequal: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=1, p: float=0.6, epsk: float=1e-6, epsilon: float=1e-10, k: int=0) -> OutputType | L1精确罚函数法 |
| lagrange_augmentedm(funcs: FuncArray, args: ArgArray, cons_equal: FuncArray, cons_unequal: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, lamk: float=6, muk: float=10, sigma: float=8, alpha: float=0.5, beta: float=0.7, p: float=2, eta: float=1e-3, epsilon: float=1e-4, k: int=0) -> OutputType | 增广拉格朗日乘子法 |
oc.mixequal.penalty_L1(f, (x1, x2), c1, c2, (1.5, 0.5), verbose=True)
(1.5, 0.5) 0.5 0
[2.5 0.5] 0.5 1
[1.47826087 1.6 ] 0.6322117202268434 2
[2.18 0.82] 0.06480000000000004 3
[1.892 1.108] 0.023328000000000043 4
[2.0648 0.9352] 0.008398079999999992 5
[1.96112 1.03888] 0.003023308800000004 6
[2.023328 0.976672] 0.001088391167999991 7
[1.9860032 1.0139968] 0.00039182082047999555 8
[2.00839808 0.99160192] 0.000141055495372801 9
[1.99496115 1.00503885] 5.0779978334209926e-05 10
[2.00302331 0.99697669] 1.8280792200315036e-05 11
[1.99818601 1.00181399] 6.581085192114058e-06 12
[2.00108839 0.99891161] 2.369190669160674e-06 13
[1.99934697 1.00065303] 8.529086408979587e-07 14
[2.00039182 0.99960818] 3.0704711072324775e-07 15
[1.99976491 1.00023509] 1.105369598604005e-07 16
[2.00014106 0.99985894] 3.9793305549762975e-08 17
(2.000141055495373, 0.9998589445046272) 3.9793305549762975e-08 18
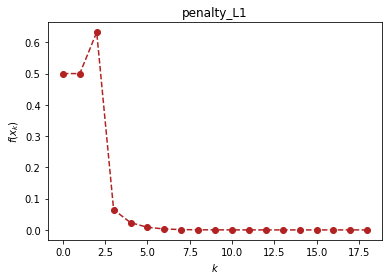
((2.000141055495373, 0.9998589445046272), 18)
相关文章:

约束优化算法(optimtool.constrain)
import optimtool as oo from optimtool.base import np, sp, pltpip install optimtool>2.4.2约束优化算法(optimtool.constrain) import optimtool.constrain as oc oc.[方法名].[函数名]([目标函数], [参数表], [等式约束表], [不等式约数表], [初…...
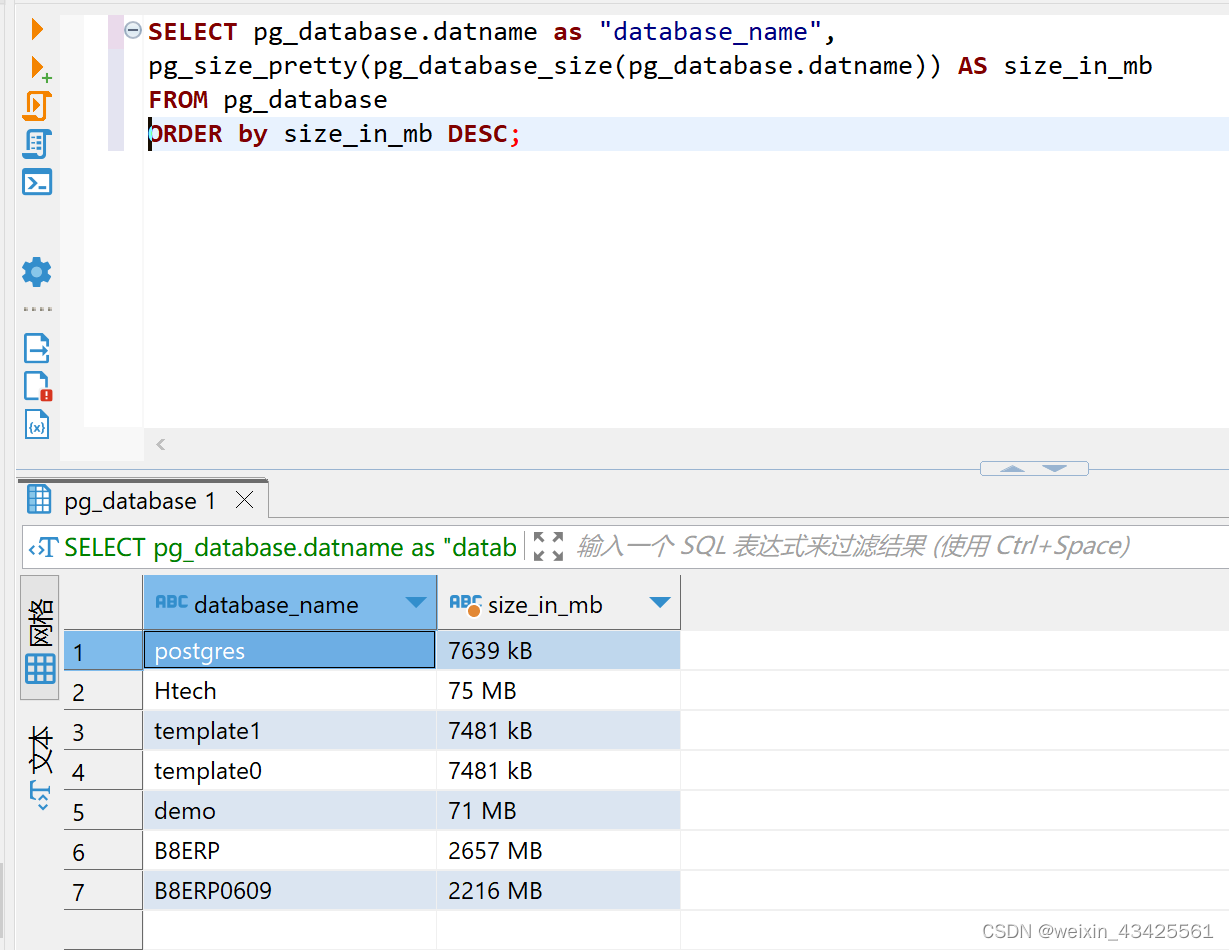
如何查看postgresql中的数据库大小?
你可以使用以下命令来查看PostgreSQL数据库的大小: SELECT pg_database.datname as "database_name", pg_size_pretty(pg_database_size(pg_database.datname)) AS size_in_mb FROM pg_database ORDER by size_in_mb DESC;这将返回一个表格࿰…...

使用python-opencv检测图片中的人像
最简单的方法进行图片中的人像检测 使用python-opencv配合yolov3模型进行图片中的人像检测 1、安装python-opencv、numpy pip install opencv-python pip install numpy 2、下载yolo模型文件和配置文件: 下载地址: https://download.csdn.net/down…...

项目进展(三)-电机驱动起来了,发现了很多关键点,也遇到了一些低级错误,
一、前言 昨天电机没有驱动起来,头发掉一堆,不过今天,终于终于终于把电机驱动起来了!!!!,特别开心,哈哈哈哈,后续继续努力完善!!&…...
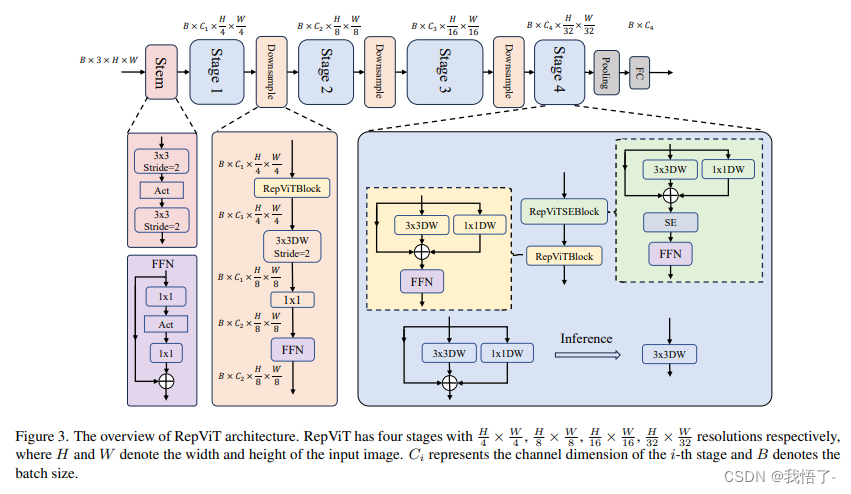
目标检测算法改进系列之Backbone替换为RepViT
RepViT简介 轻量级模型研究一直是计算机视觉任务中的一个焦点,其目标是在降低计算成本的同时达到优秀的性能。轻量级模型与资源受限的移动设备尤其相关,使得视觉模型的边缘部署成为可能。在过去十年中,研究人员主要关注轻量级卷积神经网络&a…...

学习 Kubernetes的难点和安排
Kubernetes 技术栈的特点可以用四个字来概括,那就是“新、广、杂、深”: 1.“新”是指 Kubernetes 用到的基本上都是比较前沿、陌生的技术,而且版本升级很快,经常变来变去。 2.“广”是指 Kubernetes 涉及的应用领域很多、覆盖面非…...

【MATLAB源码-第42期】基于matlab的人民币面额识别系统(GUI)。
操作环境: MATLAB 2022a 1、算法描述 基于 MATLAB 的人民币面额识别系统设计可以分为以下步骤: 1. 数据收集与预处理 数据收集: 收集不同面额的人民币照片,如 1 元、5 元、10 元、20 元、50 元和 100 元。确保在不同环境、不…...
【软件测试】软件测试的基础概念
一、一个优秀的测试人员需要具备的素质 技能方面: 优秀的测试用例设计能力:测试用例设计能力是指,无论对于什么类型的测试,都能够设计出高效的发现缺陷,保证产品质量的优秀测试用例。这就需要我们掌握设计测试用例的方…...
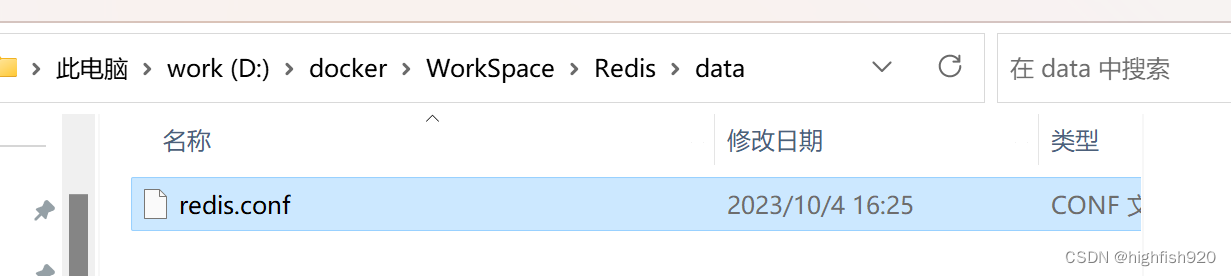
Docker-mysql,redis安装
安装MySQL 下载MySQL镜像 终端运行命令 docker pull mysql:8.0.29镜像下载完成后,需要配置持久化数据到本地 这是mysql的配置文件和存储数据用的目录 切换到终端,输入命令,第一次启动MySQL容器 docker run --restartalways --name mysq…...

五种I/O模型
目录 1、阻塞IO模型2、非阻塞IO模型3、IO多路复用模型4、信号驱动IO模型5、异步IO模型总结 blockingIO - 阻塞IOnonblockingIO - 非阻塞IOIOmultiplexing - IO多路复用signaldrivenIO - 信号驱动IOasynchronousIO - 异步IO 5种模型的前4种模型为同步IO,只有异步IO模…...

用nativescript开发ios程序常用命令?
NativeScript是一个用于跨平台移动应用程序开发的开源框架,允许您使用JavaScript或TypeScript构建原生iOS和Android应用程序。以下是一些常用的NativeScript命令,用于开发iOS应用程序: 1、创建新NativeScript项目: tns create m…...
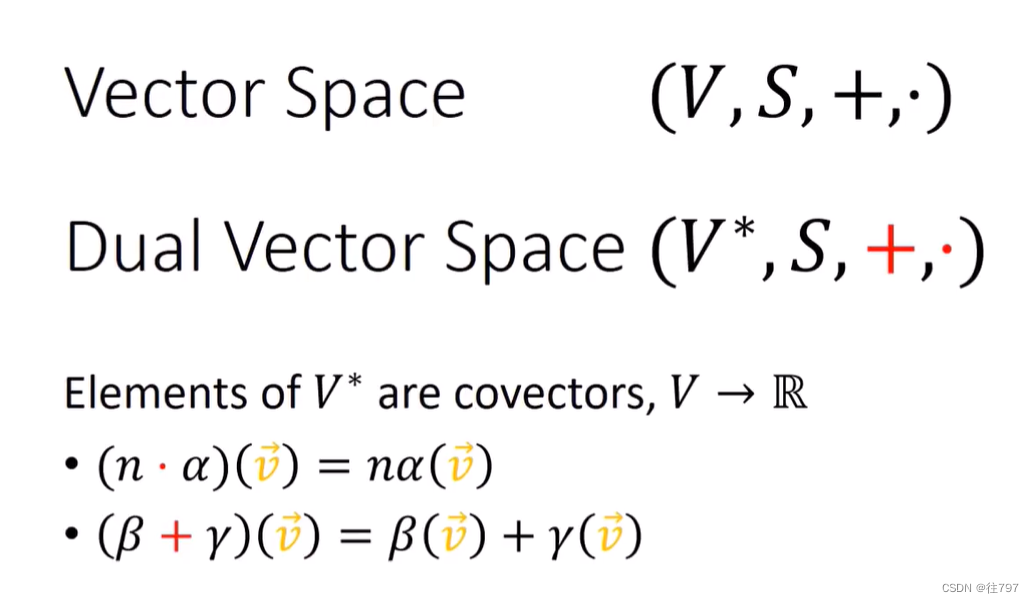
6.Tensors For Beginners-What are Convector
Covectors (协向量) What‘s a covector Covectors are “basically” Row Vectors 在一定程度上,可认为 协向量 基本上就像 行向量。 但不能简单地认为 这就是列向量进行转置! 行向量 和 列向量 是根本不同类型的对象。 …...
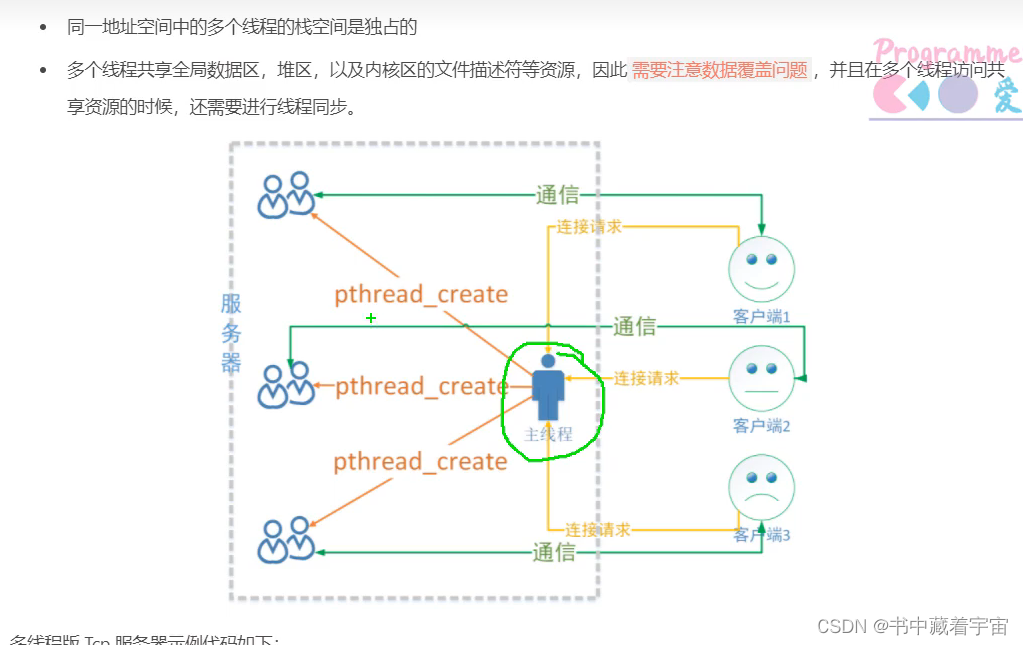
Linux多线程网络通信
思路:主线程(只有一个)建立连接,就创建子线程。子线程开始通信。 共享资源:全局数据区,堆区,内核区描述符。 线程同步不同步需要取决于线程对共享资源区的数据的操作,如果是只读就不…...

矩阵的c++实现(2)
上一次我们了解了矩阵的运算和如何使用矩阵解决斐波那契数列,这一次我们多看看例题,了解什么情况下用矩阵比较合适。 先看例题 1.洛谷P1939 【模板】矩阵加速(数列) 模板题应该很简单。 补:1<n<10^9 10^9肯定…...

RPC 框架之Thrift入门(一)
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
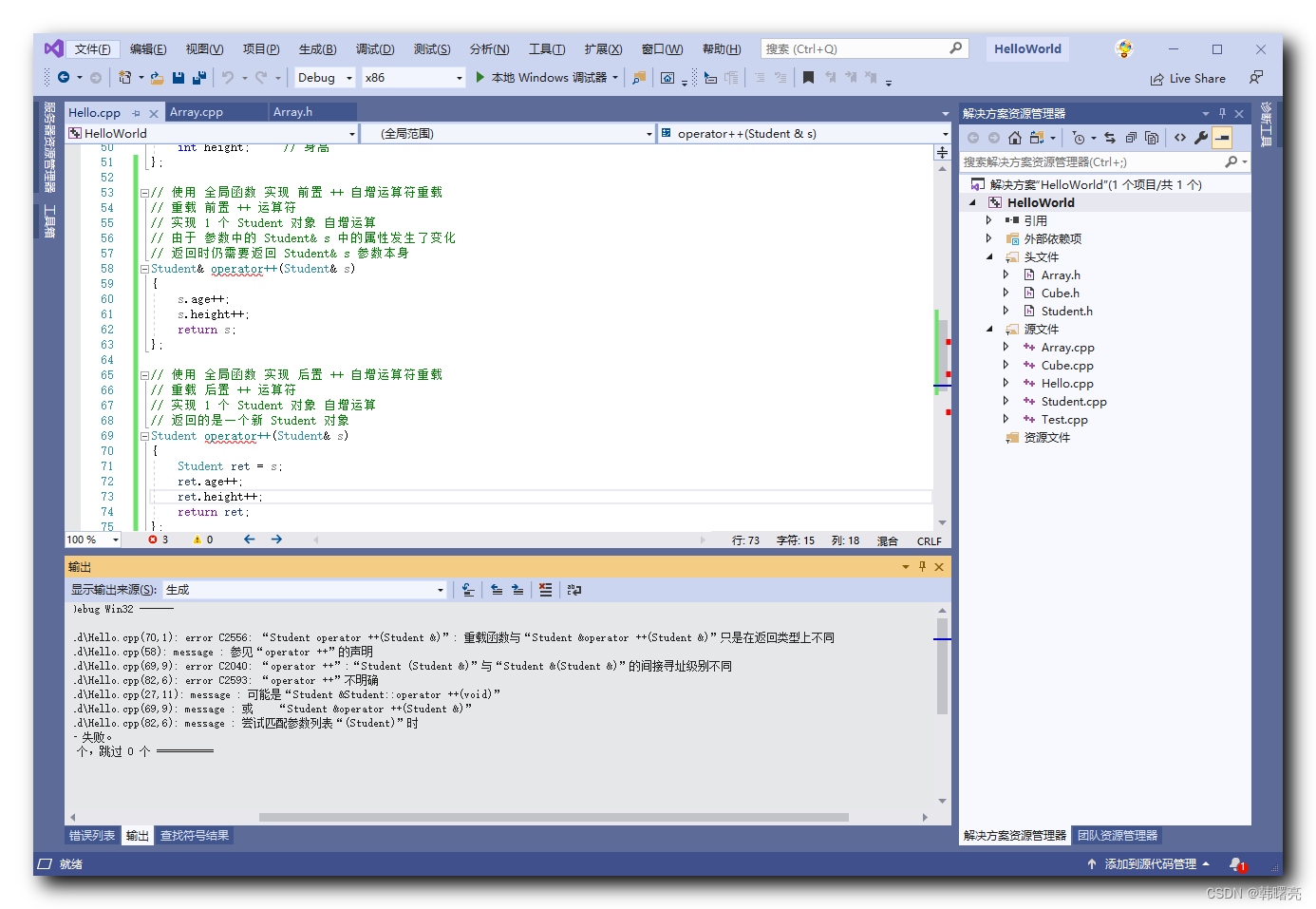
【C++】运算符重载 ⑥ ( 一元运算符重载 | 后置运算符重载 | 前置运算符重载 与 后置运算符重载 的区别 | 后置运算符重载添加 int 占位参数 )
文章目录 一、后置运算符重载1、前置运算符重载 与 后置运算符重载 的区别2、后置运算符重载添加 int 占位参数 上 2 2 2 篇博客 【C】运算符重载 ④ ( 一元运算符重载 | 使用 全局函数 实现 前置 自增运算符重载 | 使用 全局函数 实现 前置 - - 自减运算符重载 )【C】运算符…...

538. 把二叉搜索树转换为累加树
题目描述 给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束…...

java8日期时间工具类
【README】 1)本文总结了java8中日期时间常用工具方法;包括: 日期时间对象格式化为字符串;日期时间字符串解析为日期时间对象;日期时间对象转换; 转换过程中,需要注意的是: Instan…...

算法-动态规划/trie树-单词拆分
算法-动态规划/trie树-单词拆分 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/word-break/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 动态规划 2.1 解题思路 dp[i]表示[0, i)字符串可否构建那么dp[i]可构建的条件是&…...

React框架核心原理
一、整体架构 三大核心库与对应的组件 history -> react-router -> react-router-dom react-router 可视为react-router-dom 的核心,里面封装了<Router>,<Route>,<Switch>等核心组件,实现了从路由的改变到组件的更新…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
