经典算法-----汉诺塔问题
前言
今天我们学习一个老经典的问题-----汉诺塔问题,可能在学习编程之前我们就听说过这个问题,那这里我们如何去通过编程的方式去解决这么一个问题呢?下面接着看。

汉诺塔问题
问题描述
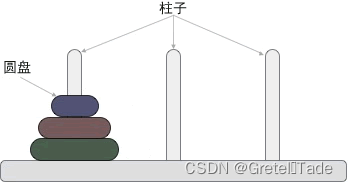
这里是引用汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上,移动过程中必须遵守以下规则:
每次只能移动柱子最顶端的一个圆盘;
每个柱子上,小圆盘永远要位于大圆盘之上;
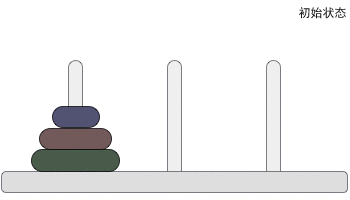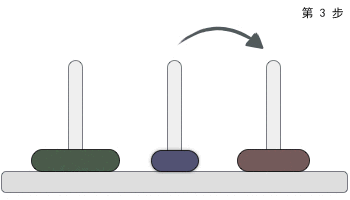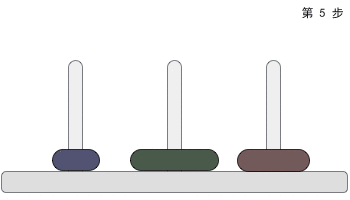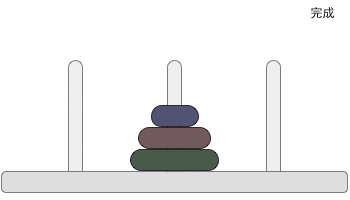
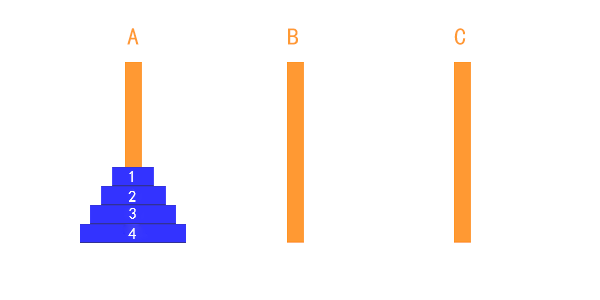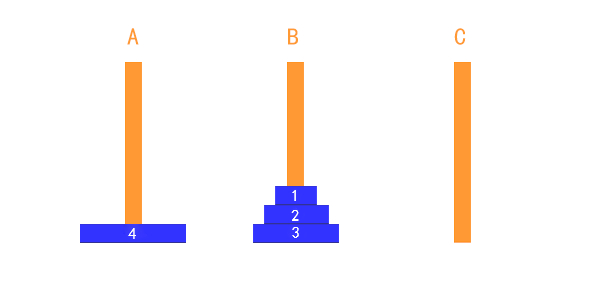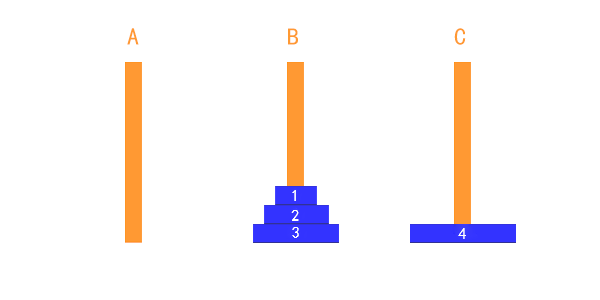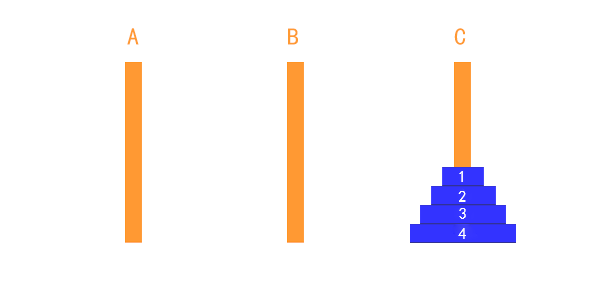
下面展示一个三个的汉诺塔解决过程,如下图所示:
其他情况:
解决思路(分治算法)
看上面这几个图,我们是否发现这么一个特点,要想把A柱子(起始柱)上的汉诺塔转移到C柱子(目标柱)上,而且还要满足汉诺塔的基本条件,那就把第三个柱子作为辅助柱(B柱),假设A柱子上有n个汉诺塔,这时候先把A柱子除了最下面的一层,其余的全部汉诺塔先放到B柱子上面,然后再把A柱子最下面的汉诺塔放到C柱子上,然后把B柱子上面的汉诺塔重新放回给A柱子当中(这个过程,C柱作为辅助柱子,B是起始柱,A是目标柱),这个过程就完成了一次放置,此时A柱子上面就剩下n-1个汉诺塔,再次重复以上的过程,最后就完成了汉诺塔的转移。
汉诺塔问题中,3 个圆盘至少需要移动 7 次,移动 n 的圆盘至少需要操作 2^n-1 次。
在汉诺塔问题中,当圆盘个数不大于 3 时,多数人都可以轻松想到移动方案,随着圆盘数量的增多,汉诺塔问题会越来越难。也就是说,圆盘的个数直接决定了汉诺塔问题的难度,解决这样的问题可以尝试用分治算法,将移动多个圆盘的问题分解成多个移动少量圆盘的小问题,这些小问题很容易解决,从而可以找到整个问题的解决方案。
代码实现(C语言)
#include<stdio.h>//打印移动的过程
void move(char x, char y) {printf("%c--->%c\n", x, y);
}//递归移动
void generate(int n,char a, char b, char c) {if (n == 0)return; //如果移动完成了就返回,开始递归运算//第一个过程,先把A柱子上的前n-1个汉诺塔移到B柱子上,再把最底下的那个汉诺塔移动到C上//此时a是起始柱子,c是目标柱,b是辅助柱 a--->cgenerate(n - 1, a, c, b);move(a, c);//第二个过程,当第一个过程完成了之后,就要把B柱子上的n-1个汉诺塔移回A柱子,这就是整体一个分支过程//此时b是起始柱,a是目标柱,c是辅助柱 b--->agenerate(n - 1, b, a, c);
}int main() {int n;printf("输入汉诺塔个数:");scanf("%d", &n);generate(n, 'A', 'B', 'C');
}
运行结果如下:

好了,以上就是本期的全部内容了,这个汉诺塔是不是很有意思呢?你学会了吗?
分享一张壁纸:
相关文章:

经典算法-----汉诺塔问题
前言 今天我们学习一个老经典的问题-----汉诺塔问题,可能在学习编程之前我们就听说过这个问题,那这里我们如何去通过编程的方式去解决这么一个问题呢?下面接着看。 汉诺塔问题 问题描述 这里是引用汉诺塔问题源自印度一个古老的传说&#x…...
博客之站项目测试报告
项目背景项目功能测试计划Bug总结升级自动化测试正常登录流程 项目背景 1:博客之站系统是采用前后端分离的方式来实现;使用MySQL、Redis数据库储存相关数据;同时部署到云服务器上。 2:包含注册页、登录页、博客列表页、个人列表页…...

k8s晋级之管理容器的计算资源
概述 在 Kubernetes 中创建工作负载时,您可以为 Pod 中的每一个容器指定其所需要的内存(RAM)大小和 CPU 数量。如果这些信息被指定了,Kubernetes 调度器可以更好的决定将 Pod 调度到哪一个节点。对于容器来说,其所需要…...

计算机竞赛 深度学习火车票识别系统
文章目录 0 前言1 课题意义课题难点: 2 实现方法2.1 图像预处理2.2 字符分割2.3 字符识别部分实现代码 3 实现效果4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 图像识别 火车票识别系统 该项目较为新颖,适…...
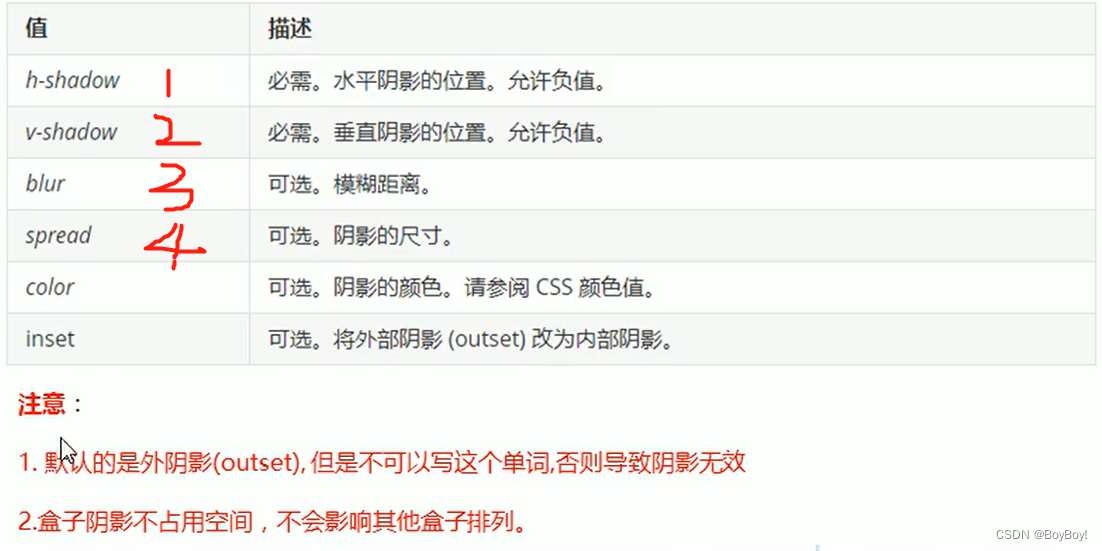
盒子阴影和网页布局
盒子阴影 box-shadow: 10px 10px 10px 4px rgba(0,0,0,.3);//最后一个是透明度 传统网页布局的三种方式 标准流 就是按照规定好的默认方式排列 1.块级元素:div、hr、p、h1~h2、ul、ol、dl、form、table 行内元素会按照书顺序,从左到右顺序排列&#…...

Ph.D,一个Permanent head Damage的群体
一个群体 Permanent head Damage 的博士生群体 Permanent head Damage Ph.D 博士生一年级的同学们,不要担忧或高兴得太早,抱歉你们还没有经历Qualification——预备考试,你们暂且不能被称为博士,只能称自己是要努力成为博士预备…...
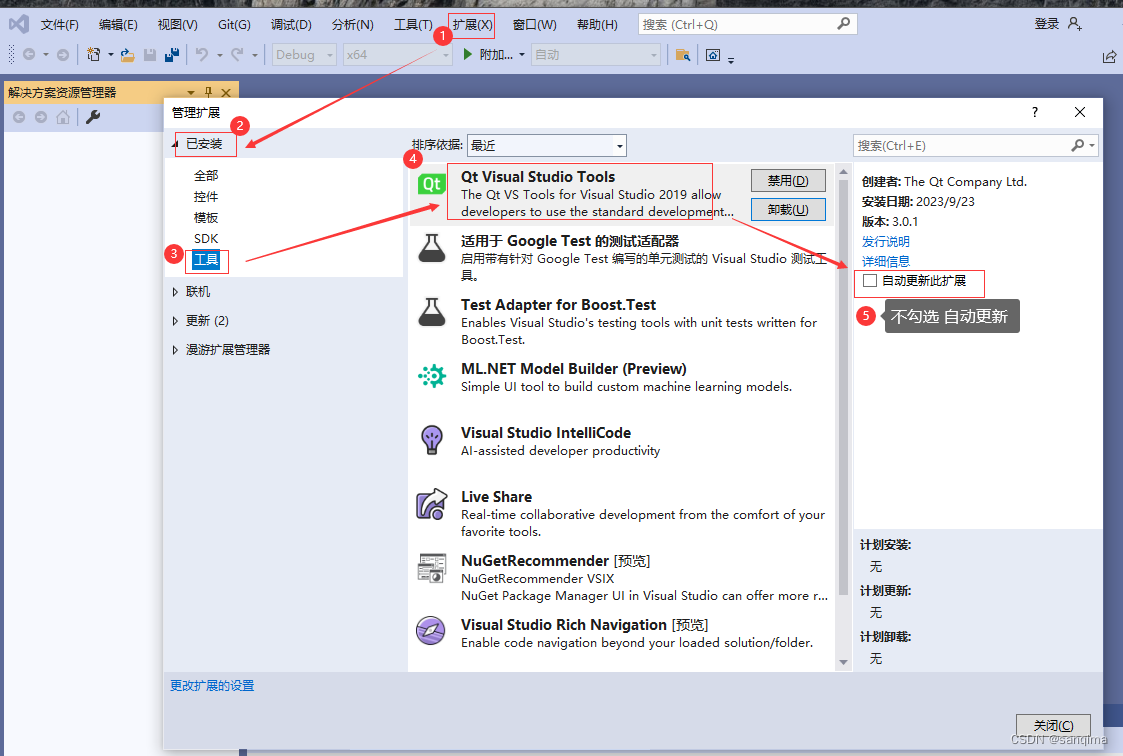
visual studio禁用qt-vsaddin插件更新
visual studio里qt-vsaddin插件默认是自动更新的,由于qt-vsaddin插件新版本的操作方式与老版本相差较大,且新版本不稳定,容易出Bug,所以需要禁用其自动更新,步骤如下: 点击VS2019菜单栏上的【扩展】–…...
Docker通过Dockerfile创建Redis、Nginx--详细过程
创建Nginx镜像 我们先创建一个目录,在目录里创建Dockerfile [rootdocker-3 ~]# mkdir mynginx [rootdocker-3 ~]# cd mynginx [rootdocker-3 ~]# vim Dockerfile Dockerfile的内容 FROM daocloud.io/library/centos:7 RUN buildDepsreadline-devel pcre-devel o…...

关于使用 uniapp Vue3 开发分享页面 语法糖 setup 开发获取ref踩坑
上代码 前端代码 <!-- 分享弹出 --> <uni-popup ref"share" type"share" safeArea backgroundColor"#fff"><uni-popup-share></uni-popup-share> </uni-popup>处理函数 import {onNavigationBarButtonTap} from…...
Springboot+vue的时间管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
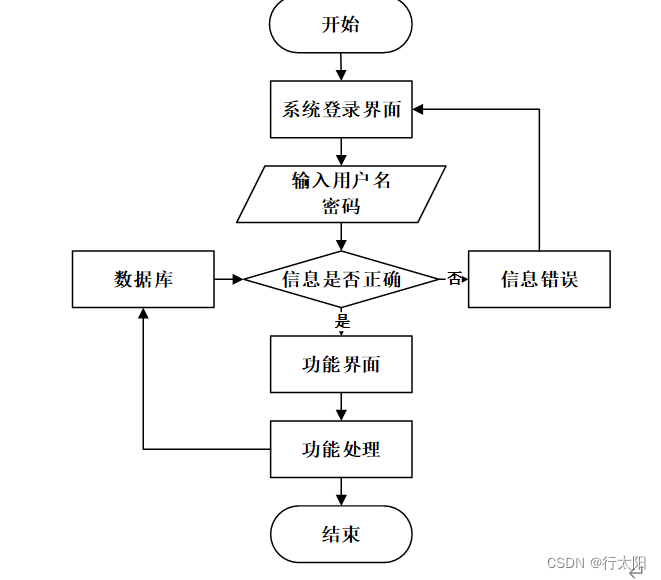
演示视频: Springbootvue的时间管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 本文设计了一个基于Springbootvue的前后端分离的时间管理系统,采用M(model࿰…...
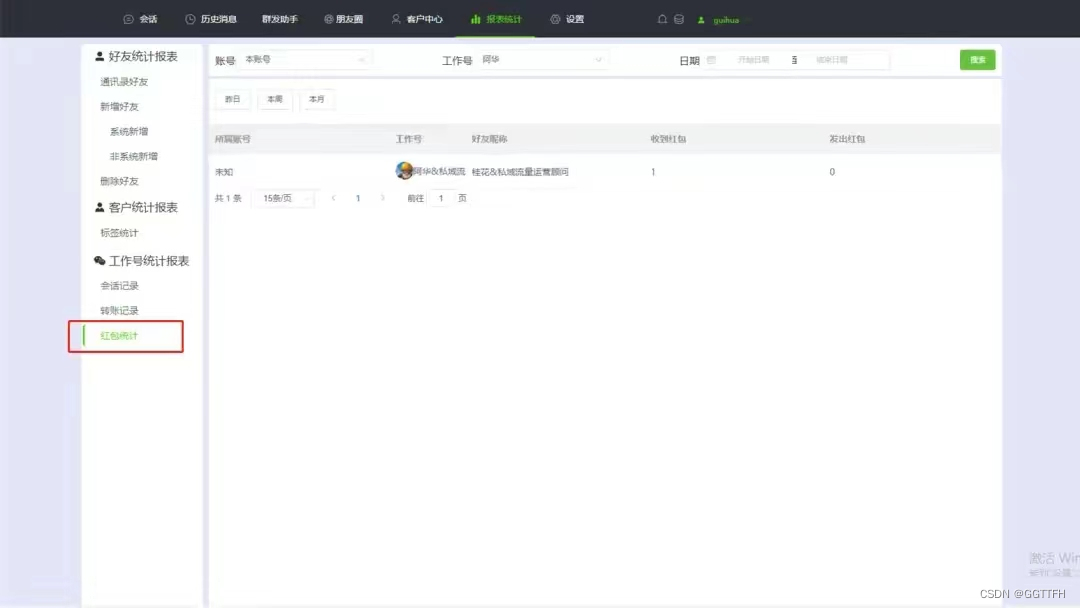
企业如何实时监管员工聊天转账行为
你还在担心员工飞单、私单吗? 你还在担心员工辱骂删除客户吗? 你还在担心员工离职会带走公司客户吗? 你还在担心员工工作不认真,工作量无法统计吗? 。。。。。。。。 在当今互联网时代,企业微信的应用已…...
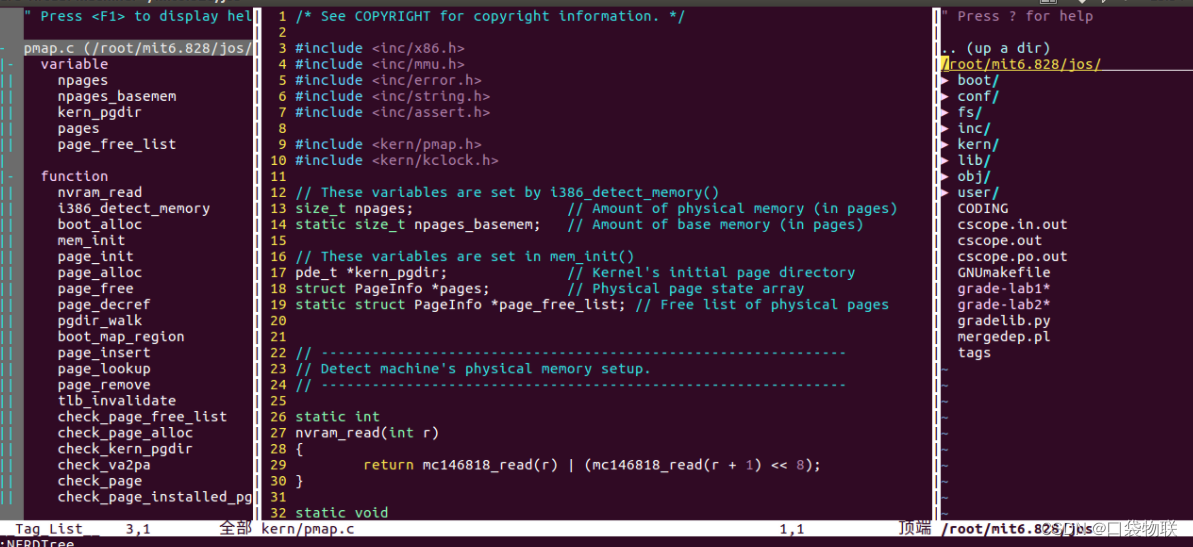
2.2.3.1vim + ctags + cscope + taglist
在window下,我们一般用Source Insight来查看代码而在linux下,使用vim来查看代码,vim是一个简单的文本浏览/编辑器,它可以通过插件的形式,搭建一个完全的类Source Insight环境,通过快捷键的形式,快速查看、定位变量/函数,本文就是基于vim,通过ctags+cscope+taglist+Ner…...

JAVA面经整理(4)
一)Volitaile关键字的作用: 1)保证多线程环境下共享变量的可见性,对于一个线程对于一个共享表变量的修改,其他线程可以立即看到修改之后的共享变量的值 2)可以增加内存屏障来放置多个指令之间的重排序 volatile的使用:常常用于一写多读的情况下ÿ…...

Python3数据科学包系列(一):数据分析实战
Python3中类的高级语法及实战 Python3(基础|高级)语法实战(|多线程|多进程|线程池|进程池技术)|多线程安全问题解决方案 Python3数据科学包系列(一):数据分析实战 Python3数据科学包系列(二):数据分析实战 认识下数据科学中数据处理基础包: (1)NumPy 俗话说: 要学会跑需先…...

【LittleXi】【MIT6.S081-2020Fall】Lab: locks
【MIT6.S081-2020Fall】Lab: locks 【MIT6.S081-2020Fall】Lab: locks内存分配实验内存分配实验准备实验目的1. 举一个例子说明修改前的**kernel/kalloc.c**中如果没有锁会导致哪些进程间竞争(races)问题2. 说明修改前的kernel/kalloc.c中锁竞争contention问题及其后果3. 解释a…...
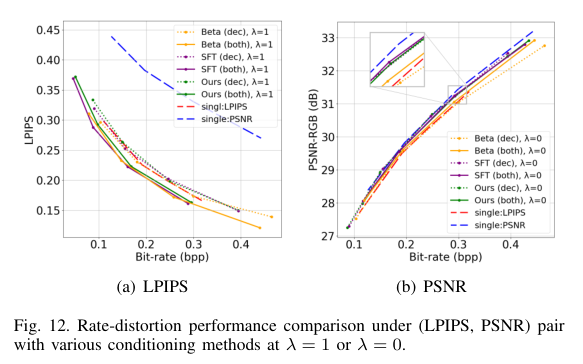
图像压缩:Transformer-based Image Compression with Variable Image Quality Objectives
论文作者:Chia-Hao Kao,Yi-Hsin Chen,Cheng Chien,Wei-Chen Chiu,Wen-Hsiao Peng 作者单位:National Yang Ming Chiao Tung University 论文链接:http://arxiv.org/abs/2309.12717v1 内容简介: 1)方向:…...

C++ 类和对象篇(四) 构造函数
目录 一、概念 1. 构造函数是什么? 2. 为什么C要引入构造函数? 3. 怎么用构造函数? 3.1 创建构造函数 3.2 调用构造函数 二、构造函数的特性 三、构造函数对成员变量初始化 0. 对构造函数和成员变量分类 1. 带参构造函数对成员变量初始化 2. …...

Swing程序设计(5)绝对布局,流布局
文章目录 前言一、布局管理器二、介绍 1.绝对布局2.流布局总结 前言 Swing窗体中,每一个组件都有大小和具体的位置。而在容器中摆放各种组件时,很难判断其组件的具体位置和大小。即一个完整的界面中,往往有多个组件,那么如何将这…...

linux基础知识之文件系统 df/du/fsck/dump2fs
du du [选项][目录或者文件名] -a 显示每个子文件等磁盘占用量,默认只统计子目录的磁盘占用量 -h 使用习惯单位显示磁盘占用量,如KB,MB或者GB -s 统计总占用量,不列出子目录和文件占用量 面向文件 du -a 16 ./.DS_Store 8 ./requi…...
华为云云耀云服务器L实例评测|Elasticsearch的Docker版本的安装和参数设置 端口开放和浏览器访问
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到各种问题,在解决问题的过程中学到不少和运维相关的知识。 本篇博客介绍Elasticsearch的Docker版本的安装和参数设置,端口开放和浏览器访问。 其他相关的华为云云…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
