离散无记忆与有记忆信源的序列熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
文章目录
- 离散无记忆信源的序列熵
- 信源的序列熵
- 离散有记忆信源的序列熵
- 平稳有记忆N次扩展源的熵
离散无记忆信源的序列熵

马尔可夫信源的特点:无后效性。
发出单个符号的信源
- 指信源每次只发出一个符号代表一个消息;
发出符号序列的信源
- 指信源每次发出一组含二个以上符号的符号序列代表一个消息。
当信源无记忆时:
p(Xˉ=xi)=p(xi1,xi2,⋯,xiL)=p(xi1)p(xi2)p(xi3)⋯p(xiL)=∏l=1Lp(xil)\begin{aligned} p(\bar{X}&\left.=x_{i}\right)=p\left(x_{i_{1}}, x_{i_{2}}, \cdots, x_{i_{L}}\right) =p\left(x_{i_{1}}\right) p\left(x_{i_{2}}\right) p\left(x_{i_{3}}\right) \cdots p\left(x_{i_{L}}\right)=\prod_{l=1}^{L} p\left(x_{i_{l}}\right) \end{aligned} p(Xˉ=xi)=p(xi1,xi2,⋯,xiL)=p(xi1)p(xi2)p(xi3)⋯p(xiL)=l=1∏Lp(xil)
信源的序列熵
H(Xˉ)=−∑i=1nLp(xi)logp(xi)=−∑i∏l=1Lp(xii)logp(xii)=∑l=1LH(Xl)\begin{aligned} H(\bar{X}) &=-\sum_{i=1}^{n^{L}} p\left(x_{i}\right) \log p\left(x_{i}\right) \\ &=-\sum_{i} \prod_{l=1}^{L} p\left(x_{i_{i}}\right) \log p\left(x_{i_{i}}\right)=\sum_{l=1}^{L} H\left(X_{l}\right) \end{aligned} H(Xˉ)=−i=1∑nLp(xi)logp(xi)=−i∑l=1∏Lp(xii)logp(xii)=l=1∑LH(Xl)
-
若又满足平稳特性(平稳信号包含的信息量小,其统计特性随时间不变化),即与序号l无关时:
p(X‾)=∏l=1Lp(xii)=pLp(\overline{\mathrm{X}})=\prod_{l=1}^{L} p\left(x_{i_{\mathrm{i}}}\right)=p^{L} p(X)=l=1∏Lp(xii)=pL
-
信源的序列熵
H(X‾)=LH(X)H(\overline{\mathrm{X}})=\operatorname{LH}(X) H(X)=LH(X)
-
平均每个符号(消息)熵(符号熵) 为
HL(Xˉ)=1LH(Xˉ)=H(X)H_{L}(\bar{X})=\frac{1}{L} H(\bar{X})=H(X) HL(Xˉ)=L1H(Xˉ)=H(X)
例: 有一个无记忆信源随机变量 X∈(0,1)\mathrm{X} \in(0,1)X∈(0,1) , 等概率分布, 若以单个符号出现为一事件, 则此时的信源熵:
H(X)=log22=1H(X)=\log _{2} 2=1H(X)=log22=1 bit/符号
即用 1 比特就可表示该事件。
如果以两个符号出现 (L=2\mathrm{L}=2L=2 的序列 )为一事件, 则随机序 列 X∈(00,01,10,11)\mathrm{X} \in(00,01,10,11)X∈(00,01,10,11) , 信源的序列熵
H(Xˉ)=log24=2H(\bar{X})=\log _{2} 4=2H(Xˉ)=log24=2 bit/序列
即用2比特才能表示该事件。
信源的符号熵
H2(X‾)=12H(X‾)=1H_{2}(\overline{\mathrm{X}})=\frac{1}{2} H(\overline{\mathrm{X}})=1H2(X)=21H(X)=1 bit/符号
- 信源的序列熵
H(X‾)=H(XL)=−∑i=19p(ai)logp(ai)=3bit/序列 H(\overline{\mathrm{X}})=H\left(X^{L}\right)=-\sum_{i=1}^{9} p\left(a_{i}\right) \log p\left(a_{i}\right)=3 b i t / \text { 序列 }H(X)=H(XL)=−∑i=19p(ai)logp(ai)=3bit/ 序列
- 平均每个符号 (消息) 熵为
H(X)=−∑i=13p(xi)logp(xi)=1.5bit/符号 H(Xˉ)=2H(X)=2×1.5=3bit/序列 \begin{array}{c} H(X)=-\sum_{i=1}^{3} p\left(x_{i}\right) \log p\left(x_{i}\right)=1.5 \text { bit/符号 } \\ H(\bar{X})=2 H(X)=2 \times 1.5=3 \mathrm{bit} / \text { 序列 } \end{array}H(X)=−∑i=13p(xi)logp(xi)=1.5 bit/符号 H(Xˉ)=2H(X)=2×1.5=3bit/ 序列
离散有记忆信源的序列熵
-
对于有记忆信源,就不像无记忆信源那样简单, 它必须引入条件熵的概念, 而且只能在某些特殊情况下才能得到一些有价值的结论。
-
对于由两个符号组成的联合信源, 有下列结论:
H(X1X2)=H(X1)+H(X2∣X1)=H(X2)+H(X1∣X2)H\left(X_{1} X_{2}\right)=H\left(X_{1}\right)+H\left(X_{2} \mid X_{1}\right)=H\left(X_{2}\right)+H\left(X_{1} \mid X_{2}\right) H(X1X2)=H(X1)+H(X2∣X1)=H(X2)+H(X1∣X2)H(X1)≥H(X1∣X2),H(X2)≥H(X2∣X1)H\left(X_{1}\right) \geq H\left(X_{1} \mid X_{2}\right), H\left(X_{2}\right) \geq H\left(X_{2} \mid X_{1}\right) H(X1)≥H(X1∣X2),H(X2)≥H(X2∣X1)
-
当前后符号无依存关系时,有下列推论:
H(X1X2)=H(X1)+H(X2)H(X1∣X2)=H(X1),H(X2∣X1)=H(X2)\begin{array}{l} H\left(X_{1} X_{2}\right)=H\left(X_{1}\right)+H\left(X_{2}\right) \\ H\left(X_{1} \mid X_{2}\right)=H\left(X_{1}\right), H\left(X_{2} \mid X_{1}\right)=H\left(X_{2}\right) \end{array} H(X1X2)=H(X1)+H(X2)H(X1∣X2)=H(X1),H(X2∣X1)=H(X2) -
若信源输出一个L长序列,则信源的序列熵为
H(X‾)=H(X1X2⋯XL)=H(X1)+H(X2∣X1)+⋯+H(XL∣XL−1⋯X1)=∑lLH(Xl∣Xl−1)=H(XL)\begin{aligned} H(\overline{\mathrm{X}}) &=H\left(X_{1} X_{2} \cdots X_{L}\right) \\ &=H\left(X_{1}\right)+H\left(X_{2} \mid X_{1}\right)+\cdots+H\left(X_{L} \mid X_{L-1} \cdots X_{1}\right) \\ &=\sum_{l}^{L} H\left(X_{l} \mid X^{l-1}\right)=H\left(X^{L}\right) \end{aligned} H(X)=H(X1X2⋯XL)=H(X1)+H(X2∣X1)+⋯+H(XL∣XL−1⋯X1)=l∑LH(Xl∣Xl−1)=H(XL)
-
平均每个符号的熵为:
HL(Xˉ)=1LH(XL)H_{L}(\bar{X})=\frac{1}{L} H\left(X^{L}\right) HL(Xˉ)=L1H(XL)
-
若当信源退化为无记忆时: 若进一步又满足平稳性时
H(Xˉ)=∑lLH(Xl)H(Xˉ)=LH(X)H(\bar{X})=\sum_{l}^{L} H\left(X_{l}\right) \quad H(\bar{X})=L H(X) H(Xˉ)=l∑LH(Xl)H(Xˉ)=LH(X)
平稳有记忆N次扩展源的熵
设 X\mathbf{X}X 为离散平稳有记忆信源, X\mathbf{X}X 的 N\mathbf{N}N 次扩展源记为 XNX^{N}XN ,
XN=[X1X2⋯XN]X^{N}=\left[X_{1} X_{2} \cdots X_{N}\right] XN=[X1X2⋯XN]
根据熵的可加性,得
H(XN)=H(X1X2⋯XN)=H(X1)+H(X2/X1)+⋯H(XN/X1⋯XN−1)H\left(X^{N}\right)=H\left(X_{1} X_{2} \cdots X_{N}\right)=H\left(X_{1}\right)+H\left(X_{2} / X_{1}\right)+\cdots H\left(X_{N} / X_{1} \cdots X_{N-1}\right) H(XN)=H(X1X2⋯XN)=H(X1)+H(X2/X1)+⋯H(XN/X1⋯XN−1)
根据平稳性和熵的不增原理,得H(XN)≤NH(X1)H\left(X^{N}\right) \leq N H\left(X_{1}\right)H(XN)≤NH(X1), 仅当无记忆信源时等式成立。
对于 X\mathrm{X}X 的 N\mathrm{N}N 次扩展源, 定义平均符号熵为:
HN(X)=1NH(XN)=1NH(X1⋯XN)H_{N}(X)=\frac{1}{N} H\left(X^{N}\right)=\frac{1}{N} H\left(X_{1} \cdots X_{N}\right) HN(X)=N1H(XN)=N1H(X1⋯XN)
信源 X\mathrm{X}X 的极限符号熵定义为:
H∞(X)=limN→∞1NH(XN)=limN→∞1NH(X1⋯XN)H_{\infty}(X)=\lim _{N \rightarrow \infty} \frac{1}{N} H(X^{N})=\lim _{N \rightarrow \infty} \frac{1}{N} H(X_{1} \cdots X_{N}) H∞(X)=N→∞limN1H(XN)=N→∞limN1H(X1⋯XN)
极限符号熵简称符号熵, 也称熵率。
定理: 对任意离散平稳信源, 若 H1(X)<∞H_{1}(X)<\inftyH1(X)<∞ , 有:
(1) H(XN/X1⋯XN−1)H\left(X_{N} / X_{1} \cdots X_{N-1}\right)H(XN/X1⋯XN−1) 不随 N\mathbf{N}N而增加;
(2) HN(X)≥H(XN/X1⋯XN−1);H_{N}(X) \geq H\left(X_{N} / X_{1} \cdots X_{N-1}\right) ;HN(X)≥H(XN/X1⋯XN−1);
(3)HN(X)H_{N}(X)HN(X) 不随 N 而增加;
(4) H∞(X)H_{\infty}(X)H∞(X) 存在,且 H∞(X)=limN→∞H(XN/X1⋯XN−1)H_{\infty}(X)=\lim _{N \rightarrow \infty} H(X_{N} / X_{1} \cdots X_{N-1})H∞(X)=limN→∞H(XN/X1⋯XN−1)
该式表明, 有记忆信源的符号熵也可通过计算极限条件熵得到。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
相关文章:

离散无记忆与有记忆信源的序列熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录离散无记忆信源的…...
算法该不该刷?如何高效刷算法?
一、算法该不该刷?最近有小伙伴向我咨询一个问题,就是算法该不该刷,该如何刷算法呢?这个问题可谓太大众化了,只要你去某乎、某度搜索一下相关的解答,会有无数种回答,可见这个问题困扰了多少学习…...
Allegro如何在关闭飞线模式下查看网络连接位置操作指导
Allegro如何在关闭飞线模式下查看网络连接位置操作指导 在用Allegro做PCB设计的时候,有时会因为设计需要,关闭飞线显示。 如何在关闭飞线显示模式下查看网络连接的位置,如下图 除了能看到网络连接的点位以外,还能看到器件的pin Number 如何显示出这种效果,具体操作如下 …...
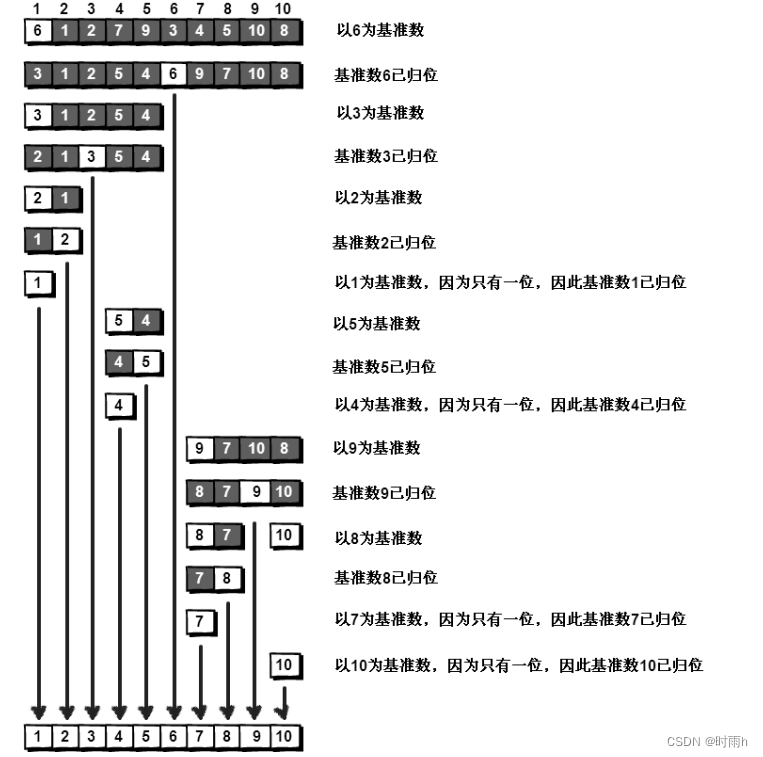
啊哈 算法读书笔记 第 1 章 一大波数正在靠近——排序
目录 排序算法: 时间复杂度: 排序算法和冒泡排序之间的过渡: 冒泡排序 冒泡排序和快速排序之间的过渡: 快速排序 排序算法: 首先出场的是我们的主人公小哼,上面这个可爱的娃就是啦。期末考试完了老…...
:HTTP请求与响应)
Servlet笔记(5):HTTP请求与响应
1、HTTP请求 当浏览器请求网页时,它会向Web服务器发送特定信息,这些信息不能被直接读取,而是通过传输HTTP请求时,封装进请求头中。 有哪些头信息? 头信息描述Accept这个头信息指定浏览器或其他客户端可以处理的 MIME…...
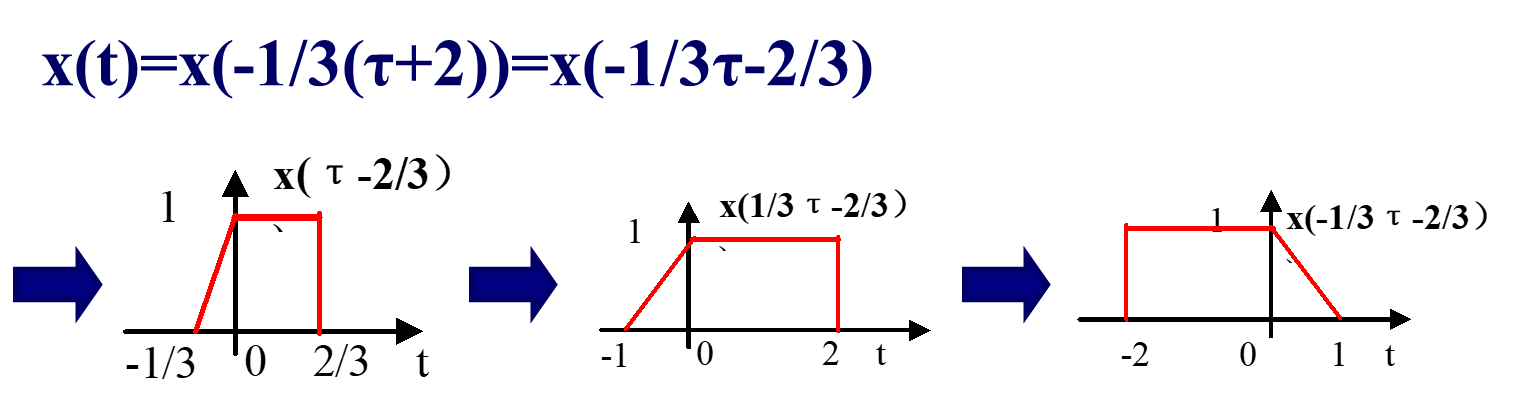
信号的运算与变换
目录 前言 本章内容介绍 信号的运算与变换 相加 相乘 时移 反折 尺度变换 微分(差分) 积分(累加) 信号的奇偶求解 信号的实虚分解 合适的例题 1、时移反折 2、时移尺度 3、时移反折尺度 4、反求x(t) 前言 《信号…...

【GO】K8s 管理系统项目9[API部分--Secret]
K8s 管理系统项目[API部分–Secret] 1. 接口实现 service/dataselector.go // secret type secretCell corev1.Secretfunc (s secretCell) GetCreation() time.Time {return s.CreationTimestamp.Time }func (s secretCell) GetName() string {return s.Name }2. Secret功能…...
ESP32 Arduino EspNow点对点双向通讯
ESP32 Arduino EspNow点对点双向通讯✨本案例分别采用esp32和esp32C3之间点对点单播无线通讯方式。 🌿esp32开发板 🌾esp32c3开发板 🔧所需库(需要自行导入到Arduino IDE library文件夹中,无法在IDE 管理库界面搜索下载到该库)&am…...
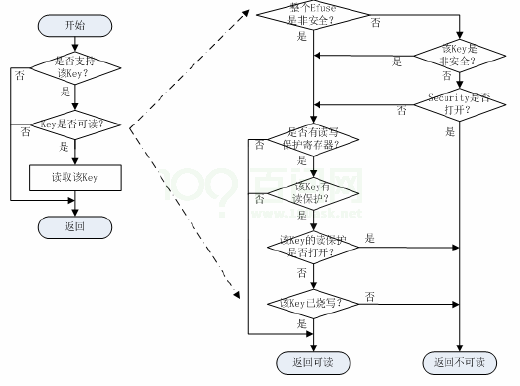
Linux SID 开发指南
Linux SID 开发指南 1 前言 1.1 编写目的 介绍Linux 内核中基于Sunxi 硬件平台的SID 模块驱动的详细设计,为软件编码和维护提供基 础。 1.2 适用范围 内核版本Linux-5.4, Linux-4.9 的平台。 1.3 相关人员 SID 驱动、Efuse 驱动、Sysinfo 驱动的维护、应用开…...
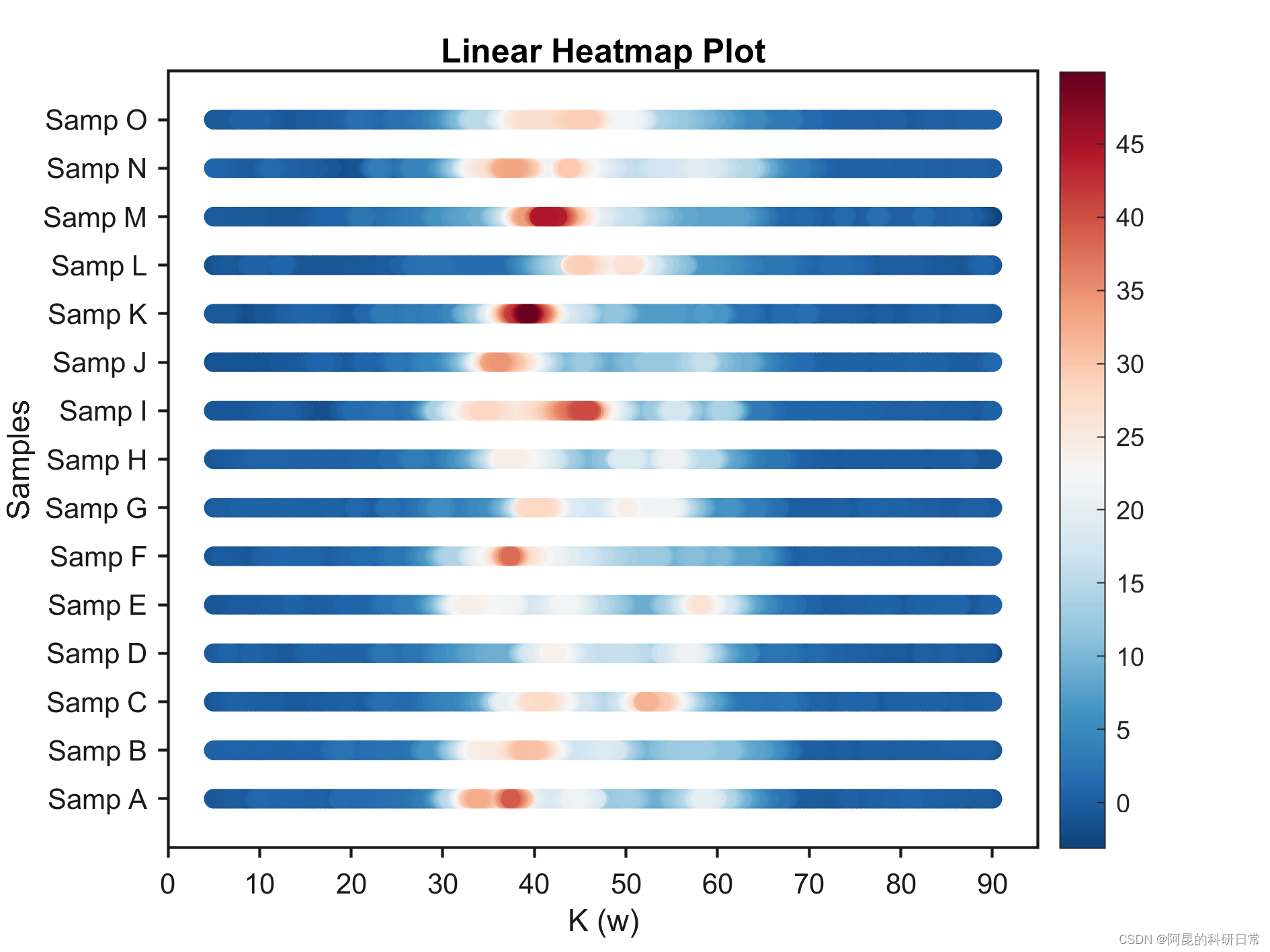
Matlab进阶绘图第2期—线型热图
线型热图由共享X轴的多条渐变直线组成,其颜色表示某一特征值。 与传统热图相比,线型热图适应于X轴数据远多于Y轴(条数)的情况,可以很好地对不同组数据间的分布情况进行比较,也因此可以在一些期刊中看到它的…...

【Redis中bigkey你了解吗?bigkey的危害?】
一.Redis中bigkey你了解吗?bigkey的危害? 如果面试官问到了这个问题,不必惊慌,接下来我们从什么是bigkey?bigkey划分的类型?bigkey危害之处? 二.什么是bigkey?会有什么影响ÿ…...
C++回顾(一)——从C到C++
前言 在学习了C语言的基础上,C到底和C有什么区别呢? 1.1 第一个C程序 #include <iostream>// 使用名为std的命名空间 using namespace std;int main() {// printf ("hello world\n");// cout 标准输出 往屏幕打印内容 相当于C语言的…...

CRF条件随机场 | 关键原理+面试知识点
😄 CRF之前跟人生导师:李航学习过,这里结合自己的理解,精简一波CRF,总结一下面试中高频出现的要点。个人觉得没网上说的那么复杂,我看网上很大部分都是一长篇先举个例子,然后再说原理。没必要原理其实不难,直接从原理下手更好理解。 文章目录 1、概率无向图(马尔可夫…...
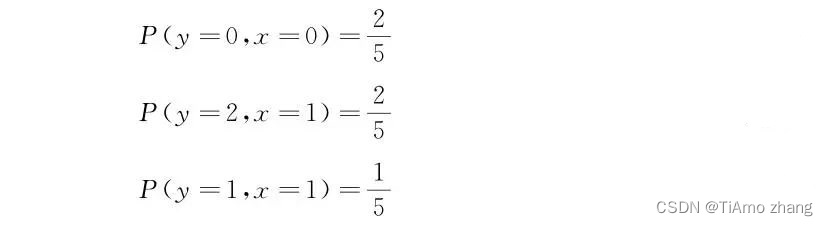
秒懂算法 | 回归算法中的贝叶斯
在本文中,我们会用概率的观点来看待机器学习模型,用简单的例子帮助大家理解判别式模型和生成式模型的区别。通过思考曲线拟合的问题,发现习以为常的损失函数和正则化项背后有着深刻的意义 01、快速理解判别式模型和生成式模型 从概率的角度来理解数据有着两个不同的角度,假…...

用Netty实现物联网01:XML-RPC和JSON-RPC
最近十年,物联网和云计算、人工智能等技术一道,受到业内各方追捧,被炒得火热,甚至还诞生了AIoT这样的技术概念。和(移动)互联网不同,物联网针对的主要是一些资源有限的硬件设备,比如监控探头、烟雾感应器、温湿度感应器、车载OBD诊断器、智能电表、智能血压计等。这些硬…...

腾讯云服务器centos7安装python3.7+,解决ssl问题
使用requests模块访问百度,报错如下: requests.exceptions.SSLError: HTTPSConnectionPool(hostwww.baidu.com, port443): Max retries exceeded with url: / (Caused by SSLError("Cant connect to HTTPS URL because the SSL module is not avail…...

C++【模板STL简介】
文章目录C模板&&STL初阶一、泛型编程二、函数模板2.1.函数模板概念2.2.函数模板格式2.3.函数模板的实例化2.4.模板参数的匹配原则三、 类模板3.1.模板的定义格式3.2.类模板的实例化STL简介一、STL的概念、组成及缺陷二、STL的版本C模板&&STL初阶 一、泛型编程…...

该学会是自己找bug了(vs调试技巧)
前言 🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻推荐专栏: 🍔🍟🌯 c语言初阶 🔑个人信条: 🌵知行合一 🍉本篇简介:>:介绍c语言初阶的最后一篇.有关调试的重要性. 金句分享…...
)
Redis大全(概念与下载安装)
目录 一、概念 1.非关系型数据库(NoSQL)的介绍 2.什么是redis 3.redis的作者 4.Redis的特点 5.redis的应用场景 6.高度概括知识 一、二 缓存穿透、缓存击穿、缓存雪崩的概念 (一)缓存穿透 (二)缓…...

指针的进阶【上篇】
文章目录📀1.字符指针📀2.指针数组📀3.数组指针💿3.1.数组指针的定义💿3.2. &数组名VS数组名💿3.3.数组指针的使用📀1.字符指针 int main() {char ch w;char* pc &ch;// pc就是字符指…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
