AcWing 288. 休息时间,《算法竞赛进阶指南》
288. 休息时间 - AcWing题库
在某个星球上,一天由 N 个小时构成,我们称 0 点到 1 点为第 1 个小时、1 点到 2 点为第 2 个小时,以此类推。
在第 i 个小时睡觉能够恢复 Ui 点体力。
在这个星球上住着一头牛,它每天要休息 B 个小时。
它休息的这 B 个小时不一定连续,可以分成若干段,但是在每段的第一个小时,它需要从清醒逐渐入睡,不能恢复体力,从下一个小时开始才能睡着。
为了身体健康,这头牛希望遵循生物钟,每天采用相同的睡觉计划。
另外,因为时间是连续的,即每一天的第 N 个小时和下一天的第 1 个小时是相连的(N 点等于 0 点),这头牛只需要在每 N 个小时内休息够 B 个小时就可以了。
请你帮忙给这头牛安排一个睡觉计划,使它每天恢复的体力最多。
输入格式
第 1 行输入两个空格隔开的整数 N 和 B。
第 2..N+1行,第 i+1行包含一个整数 Ui。
输出格式
输出一个整数,表示恢复的体力值。
数据范围
3≤N≤3830
2≤B<N
0≤Ui≤200000
输入样例:
5 3
2
0
3
1
4
输出样例:
6
样例解释
这头牛每天 3 点入睡,睡到次日 1 点,即[1,4,2] 时间段休息,每天恢复体力值最大,为 0+4+2=6。
解析:
DP的核心思想是用集合来表示一类方案,然后从集合的维度来考虑状态之间的递推关系。
这里可以将集合划分为第 i 个小时睡与不睡
具体为:f[i][j][1] 表示前 i 个小时睡了 j 个小时,1 表示第 i 个小时睡了,0 表示第i个小时没睡
则 f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1])
f[i][j][1]=max(f[i-1][j-1][0],f[i-1][j-1][1]+w[i])
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 4e3, INF = 0x3f3f3f3f;
int n, m;
int w[N];
int f[2][N][2];int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {scanf("%d", &w[i]);}memset(f, -0x3f, sizeof(f));f[1][0][0] = f[1][1][1] = 0;for (int i = 2; i <= n; i++) {for (int j = 0; j <= m; j++) {f[i & 1][j][0] = max(f[i - 1 & 1][j][0], f[i - 1 & 1][j][1]);f[i & 1][j][1] = -INF;if (j)f[i & 1][j][1] = max(f[i - 1 & 1][j - 1][0], f[i - 1 & 1][j - 1][1] + w[i]);}}int ret = f[n & 1][m][0];memset(f, -0x3f, sizeof(f));f[1][0][0] = 0, f[1][1][1] = w[1];for (int i = 2; i <= n; i++) {for (int j = 0; j <= m; j++) {f[i & 1][j][0] = max(f[i - 1 & 1][j][0], f[i - 1 & 1][j][1]);f[i & 1][j][1] = -INF;if (j)f[i & 1][j][1] = max(f[i - 1 & 1][j - 1][0], f[i - 1 & 1][j - 1][1] + w[i]);}}ret = max(ret, f[n & 1][m][1]);cout << ret << endl;return 0;
}相关文章:

AcWing 288. 休息时间,《算法竞赛进阶指南》
288. 休息时间 - AcWing题库 在某个星球上,一天由 N 个小时构成,我们称 0 点到 1 点为第 1 个小时、1 点到 2 点为第 2 个小时,以此类推。 在第 i 个小时睡觉能够恢复 Ui 点体力。 在这个星球上住着一头牛,它每天要休息 B 个小…...

ES6中字符串的扩展
字符串的遍历器接口 使用for…of for(let x of foo) {console.log(x); } // f; o; oat() ES5中的charAt()方法,返回字符串给定位置的字符。但是不能识别码点大于0xFFFF的字符,at方法可以 includes()、startsWith()、endsWith() 用来确定一个字符串是…...
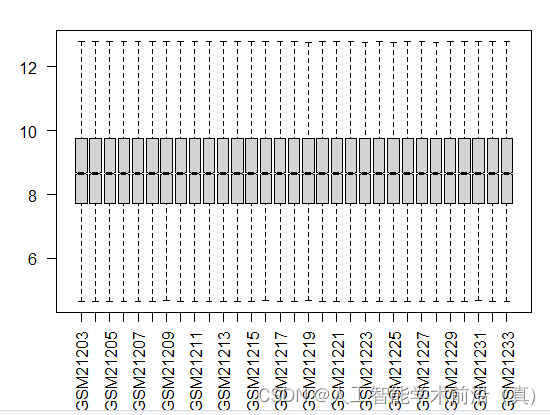
GEO生信数据挖掘(四)数据清洗(离群值处理、低表达基因、归一化、log2处理)
检索到目标数据集后,开始数据挖掘,本文以阿尔兹海默症数据集GSE1297为例 目录 离群值处理 删除 低表达基因 函数归一化,矫正差异 数据标准化—log2处理 完整代码 上节围绕着探针ID和基因名称做了一些清洗工作,还做了重复值检查…...

CI/CD工具中的CI和CD的含义
CI/CD工具中的CI和CD的含义? CI/CD 是现代软件开发方法中广泛使用的一种方法。其中,CI 代表持续集成(Continuous Integration),CD 则有两层含义,一是持续交付(Continuous Delivery)…...

用go获取IPv4地址,WLAN的IPv4地址,本机公网IP地址详解
文章目录 获取IPv4地址获取WLAN的IPv4地址获取本机公网IP地址 获取IPv4地址 下面的代码会打印出本机所有的IPv4地址。这个方法可能会返回多个IP地址,因为一台机器可能有多个网络接口,每个接口可能有一个或多个IP地址。 package mainimport ("fmt&…...

Android自定义Drawable---灵活多变的矩形背景
Android自定义Drawable—灵活多变的矩形背景 在安卓开发中,我们通常需要为不同的按钮设置不同的背景以实现不同的效果,有时还需要这些按钮根据实际情况进行变化。如果采用编写resource中xml文件的形式,就需要重复定义许多只有微小变动的资源…...

ParagonNTFSforMac_15.5.102中文版最受欢迎的NTFS硬盘格式读取工具
Paragon NTFS for Mac是一款可以为您轻松解决Mac平台上不能识别Windows通用的NTFS文件难题,这是一款强大的Mac读写工具,相信在很多时候,Mac用户需要对NTFS文件的移动硬盘进行写入,但是macOS系统默认是不让写入的,使用小…...

Kafka 搭建过程
目录 1.关于Kafka2.Kafka 搭建过程3.参考 本文主要介绍Kafka基本原理,以及搭建过程。 1.关于Kafka Apache Kafka是一个开源的分布式事件流平台,被设计用来实现实时数据流的发布、订阅、存储和处理。 Kafka的主要特性包括: 高吞吐量&#x…...
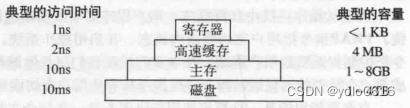
七、2023.10.1.Linux(一).7
文章目录 1、 Linux中查看进程运行状态的指令、查看内存使用情况的指令、tar解压文件的参数。2、文件权限怎么修改?3、说说常用的Linux命令?4、说说如何以root权限运行某个程序?5、 说说软链接和硬链接的区别?6、说说静态库和动态…...
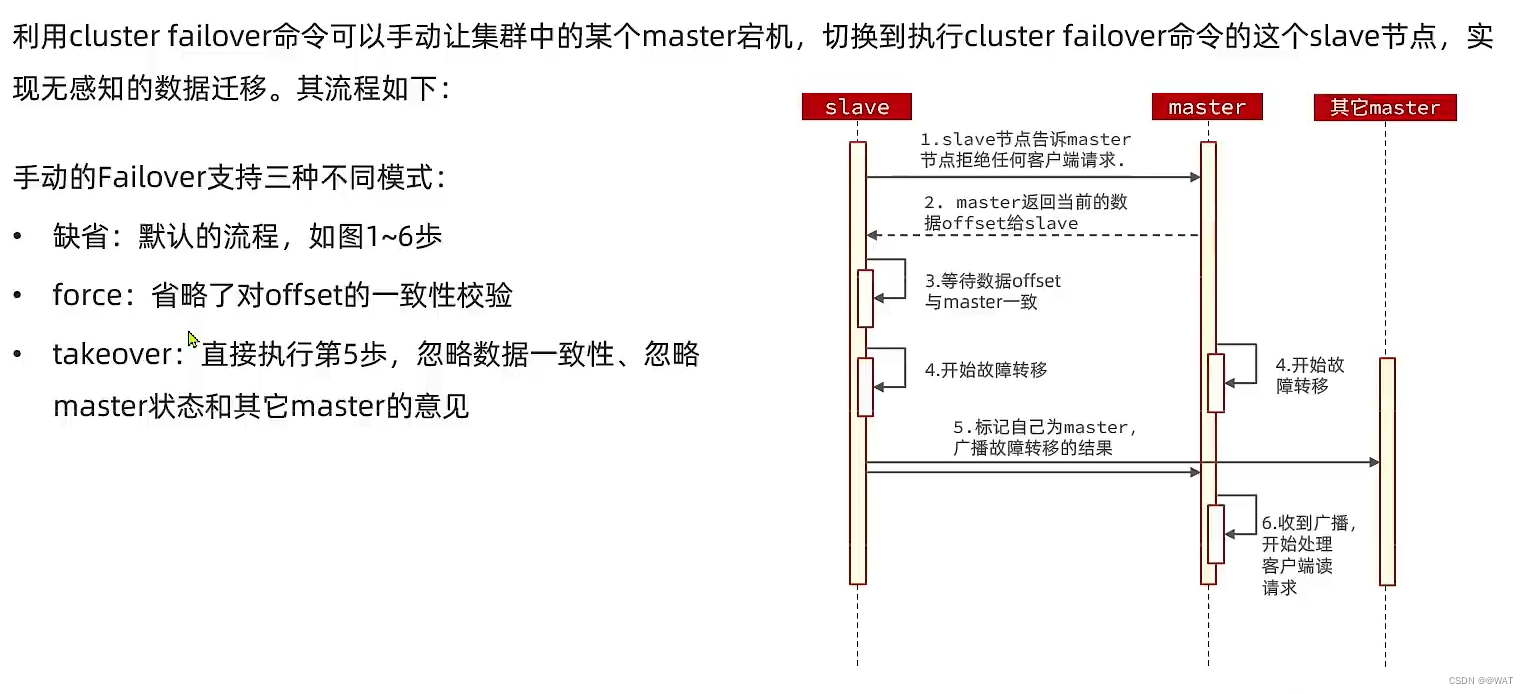
一文教你搞懂Redis集群
一、Redis主从 1.1、搭建主从架构 单节点的Redis的并发能力是有上限的,要进一步的提高Redis的并发能力,据需要大家主从集群,实现读写分离。 共包含三个实例,由于资源有限,所以在一台虚拟机上,开启多个red…...

树上启发式合并 待补
对于每个子树,直接遍历所有轻儿子,继承重儿子 会了板子后,修改维护的东西和莫队是一样的 洛谷 U41492 #include <bits/stdc.h> #define ll long long #define ull unsigned long long constexpr int N1e55; std::vector<int> e…...

minio分布式文件存储
基本介绍 什么是 MinIO MinIO 是一款基于 Go 语言的高性能、可扩展、云原生支持、操作简单、开源的分布式对象存储产品。基于 Apache License v2.0 开源协议,虽然轻量,却拥有着不错的性能。它兼容亚马逊S3云存储服务接口。可以很简单的和其他应…...

Linux新的IO模型io_uring
一、Linux下的网络通信模型 在网络开发的过程中,需要处理好几个问题。首先是通信的内核支持问题;其次是通信的模型问题;最后是框架问题。这些问题在闭源的OS如Windows上,基本上不算什么大问题(因为只能用人家的API&am…...
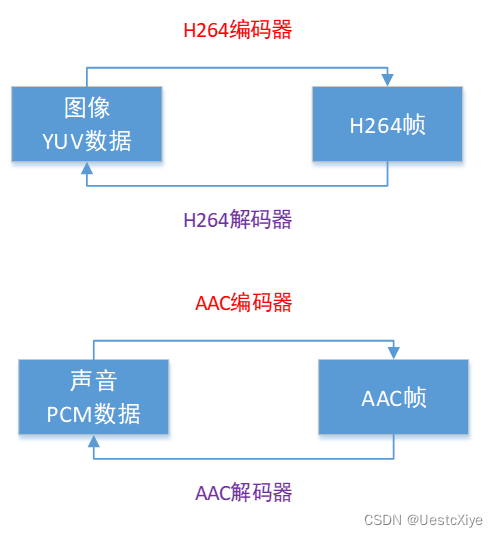
FFmpeg 命令:从入门到精通 | FFmpeg 基本介绍
FFmpeg 命令:从入门到精通 | FFmpeg 基本介绍 FFmpeg 命令:从入门到精通 | FFmpeg 基本介绍FFmpeg 简介FFmpeg 基础知识复用与解复用编解码器码率和帧率 资料 FFmpeg 命令:从入门到精通 | FFmpeg 基本介绍 本系列文章要解决的问题࿱…...

数组篇 第一题:删除排序数组中的重复项
更多精彩内容请关注微信公众号:听潮庭。 第一题:删除排序数组中的重复项 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应…...
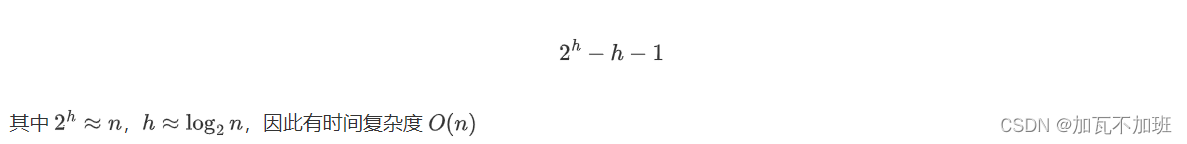
堆的初步认识
在学习本节文章前要先了解:大顶堆与小顶堆: (优先级队列_加瓦不加班的博客-CSDN博客) 堆实现 计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。 什么叫完全二叉树? 答&#x…...

CycleGAN模型之Pytorch实战
一、CycleGAN基本介绍 1. CycleGAN论文:《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》 2. 原文代码:https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix 3. 网传精简代码:https://github.com/aitorzip/PyTorch-CycleGAN …...
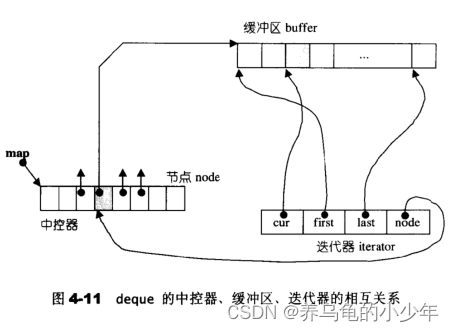
C++(STL容器适配器)
前言: 适配器也称配接器(adapters)在STL组件的灵活组合运用功能上,扮演着轴承、转换器的角色。 《Design Patterns》对adapter的定义如下:将一个class的接口转换为另一个class的接口,使原本因接口不兼容而…...
)
软考 系统架构设计师系列知识点之软件架构风格(7)
接前一篇文章:软考 系统架构设计师系列知识点之软件架构风格(6) 这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格(水平)考试,11月4号就要考试,因此…...

【Vue3】自定义指令
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令 (Custom Directives)。 1. 生命周期钩子函数 一个自定义指令由一个包含类似组件生命周期钩子的对象来定义。钩子函数会接收到指令所绑定元素作为其参数。 在 <script …...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
