【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 4. 对坐标的曲面积分(第二类曲面积分)与场论初步
文章目录
- 二、曲面积分
- 2.2 对坐标的曲面积分(第二类曲面积分)
- 1. 问题产生 —— 流量
- 2. 对坐标的曲面积分的定义(了解)
- 3. 对坐标的曲面积分的性质
- 4. 对坐标的曲面积分的计算法
- (1) 二重积分法
- (2)高斯公式
- 5. 两类曲面积分之间的关系
- 三、场论初步
- 3.1 梯度、旋度、散度
- 3.2 通量与环流量
- 写在最后
二、曲面积分
2.2 对坐标的曲面积分(第二类曲面积分)
1. 问题产生 —— 流量
设 Σ \varSigma Σ 为有侧曲面,流体的流速为 v → = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{v}=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} v={P(x,y,z),Q(x,y,z),R(x,y,z)} ,单位时间内流过指定侧的曲面的流量 Φ \varPhi Φ 的计算思路(元素法)如下:
(1)任取 d S → = { d y d z , d z d x , d x d y } ⊂ Σ d\overrightarrow{S}=\{dydz,dzdx,dxdy\}\sub \varSigma dS={dydz,dzdx,dxdy}⊂Σ ;
(2) d Φ = v → ⋅ d S → = P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y d\varPhi=\overrightarrow{v}\cdot d\overrightarrow{S}=P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy dΦ=v⋅dS=P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy ;
(3) Φ = ∬ Σ d Φ = ∬ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y \varPhi=\iint_{\varSigma}d\varPhi=\iint_{\varSigma}P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy Φ=∬ΣdΦ=∬ΣP(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy 。
2. 对坐标的曲面积分的定义(了解)

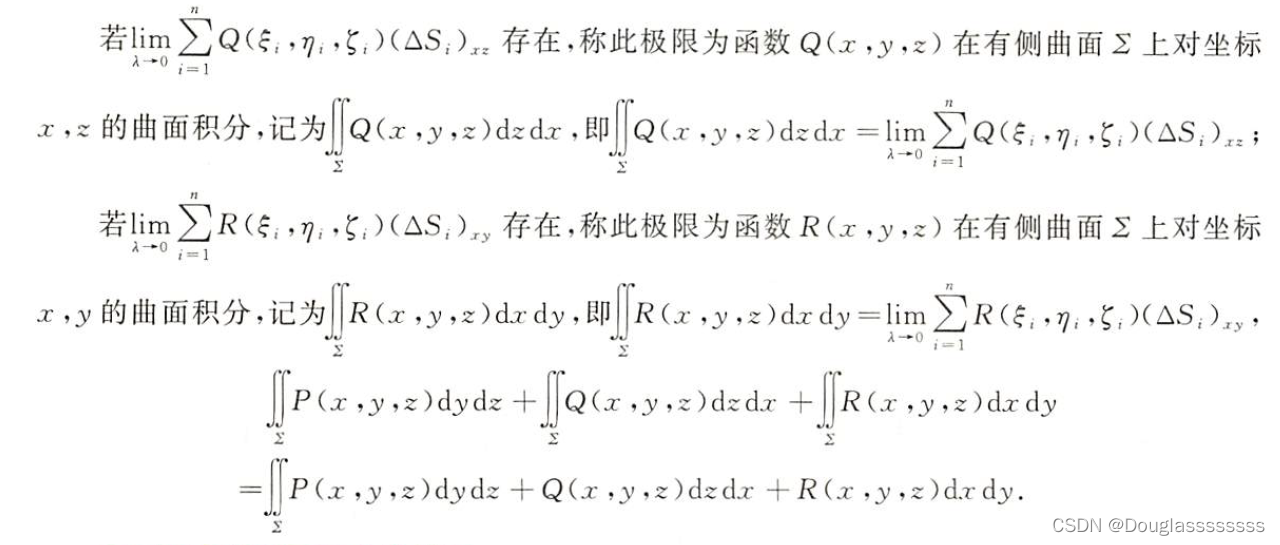
3. 对坐标的曲面积分的性质
这里说明几点特殊的,积分区域 Σ \varSigma Σ 是有方向的,不同方向得到的积分结果互为相反数;对坐标的曲面积分也具有对称性,不过若关于 x O y xOy xOy 面(变量 z z z ),只需要判断 R ( x , y , z ) R(x,y,z) R(x,y,z) 关于 z z z 的奇偶性。需要注意的是,如果是奇函数,结果是两倍,偶函数才为零,这和前面是截然相反的!
4. 对坐标的曲面积分的计算法
(1) 二重积分法
对 ∬ Σ R ( x , y , z ) d x d y \iint_\varSigma R(x,y,z)dxdy ∬ΣR(x,y,z)dxdy 的计算:设 Σ : z = u ( x , y ) \varSigma:z=u(x,y) Σ:z=u(x,y) ,其中 ( x , y ) ∈ D x y (x,y)\in D_{xy} (x,y)∈Dxy ,则 ∬ Σ R ( x , y , z ) d x d y = ± ∬ Σ R ( x , y , u ( x , y ) ) d x d y . \iint_{\varSigma} R(x,y,z)dxdy=\pm\iint_{\varSigma} R(x,y,u(x,y))dxdy. ∬ΣR(x,y,z)dxdy=±∬ΣR(x,y,u(x,y))dxdy. 其中,若 Σ \varSigma Σ 上一点的正侧法向量与 z z z 轴的夹角为锐角,结果取正,否则取负。
其余两个情形可同理进行计算。
【例】设 Σ : ( x − 1 ) 2 + y 2 + z 2 = 1 \varSigma:(x-1)^2+y^2+z^2=1 Σ:(x−1)2+y2+z2=1 ,取外侧,计算 ∬ Σ y 2 z d x d y \iint_{\varSigma}y^2z\space dxdy ∬Σy2z dxdy 。
解: 易知, Σ \varSigma Σ 表示的是一个球面,关于 x O y xOy xOy 面对称,设上半球面为 Σ 1 \varSigma_1 Σ1 ,有 ∬ Σ y 2 z d x d y = 2 ∬ Σ 1 y 2 z d x d y , \iint_{\varSigma}y^2z\space dxdy=2\iint_{\varSigma_1}y^2z\space dxdy, ∬Σy2z dxdy=2∬Σ1y2z dxdy, 令 Σ 1 : z = 1 − ( x − 1 ) 2 − y 2 , ( x , y ) ∈ D x y , D x y : ( x − 1 ) 2 + y 2 ≤ 1 \varSigma_1:z=\sqrt{1-(x-1)^2-y^2},(x,y)\in D_{xy},D_{xy}:(x-1)^2+y^2\leq1 Σ1:z=1−(x−1)2−y2,(x,y)∈Dxy,Dxy:(x−1)2+y2≤1 ,则 ∬ Σ y 2 z d x d y = 2 ∬ D x y y 2 1 − ( x − 1 ) 2 − y 2 d x d y , \iint_{\varSigma}y^2z\space dxdy=2\iint_{D_{xy}}y^2\sqrt{1-(x-1)^2-y^2}dxdy, ∬Σy2z dxdy=2∬Dxyy21−(x−1)2−y2dxdy, 令 x = 1 + r cos θ , y = r sin θ , θ ∈ [ 0 , 2 π ] , r ∈ [ 0 , 1 ] x=1+r\cos\theta,y=r\sin\theta,\theta\in[0,2\pi],r\in[0,1] x=1+rcosθ,y=rsinθ,θ∈[0,2π],r∈[0,1] ,有 2 ∬ D x y y 2 1 − ( x − 1 ) 2 − y 2 d x d y = 2 ∫ 0 2 π sin 2 θ d θ ∫ 0 1 r 3 1 − r 2 d r = 4 π 15 . 2\iint_{D_{xy}}y^2\sqrt{1-(x-1)^2-y^2}dxdy=2\int_0^{2\pi}\sin^2\theta d\theta\int_0^1r^3\sqrt{1-r^2}dr=\frac{4\pi}{15}. 2∬Dxyy21−(x−1)2−y2dxdy=2∫02πsin2θdθ∫01r31−r2dr=154π.
(2)高斯公式
定理 —— 设 Ω \Omega Ω 为几何体, Σ \varSigma Σ 为 Ω \Omega Ω 的外侧曲面, P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x,y,z),Q(x,y,z),R(x,y,z) P(x,y,z),Q(x,y,z),R(x,y,z) 在 Ω \Omega Ω 上一阶连续可偏导,则 ∯ Σ P d y d z + Q d z d x + R d x d y = ∭ Ω ( ∂ P / ∂ x + ∂ Q / ∂ y + ∂ R / ∂ z ) d v . \oiint_{\varSigma}Pdydz+Qdzdx+Rdxdy=\iiint_{\Omega}(\partial P/\partial x+\partial Q/\partial y+\partial R/\partial z)dv. ∬ΣPdydz+Qdzdx+Rdxdy=∭Ω(∂P/∂x+∂Q/∂y+∂R/∂z)dv.
【例】计算 ∯ Σ x z 2 d y d z + ( x 2 y − z 3 ) d z d x + ( 2 x y + y 2 z ) d x d y \oiint_{\varSigma}xz^2dydz+(x^2y-z^3)dzdx+(2xy+y^2z)dxdy ∬Σxz2dydz+(x2y−z3)dzdx+(2xy+y2z)dxdy ,其中 Σ \varSigma Σ 为 z = 1 − x 2 − y 2 z=\sqrt{1-x^2-y^2} z=1−x2−y2 和 z = 0 z=0 z=0 所围区域表面外侧,如下图所示。

解: 由高斯公式可知: ∯ Σ x z 2 d y d z + ( x 2 y − z 3 ) d z d x + ( 2 x y + y 2 z ) d x d y = ∭ Ω ( z 2 + x 2 + y 2 ) d v = ∫ 0 2 π d θ ∫ 0 π / 2 d φ ∫ 0 1 r 2 r 2 sin φ d r = 2 π / 5. \oiint_{\varSigma}xz^2dydz+(x^2y-z^3)dzdx+(2xy+y^2z)dxdy=\iiint_{\Omega}(z^2+x^2+y^2)dv=\int_0^{2\pi}d\theta\int_0^{\pi/2}d\varphi\int_0^1r^2r^2\sin\varphi dr=2\pi/5. ∬Σxz2dydz+(x2y−z3)dzdx+(2xy+y2z)dxdy=∭Ω(z2+x2+y2)dv=∫02πdθ∫0π/2dφ∫01r2r2sinφdr=2π/5.
5. 两类曲面积分之间的关系
∯ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ ( P c o s α + Q cos β + R cos γ ) d S . \oiint_{\varSigma}Pdydz+Qdzdx+Rdxdy=\iint_{\varSigma}(Pcos\alpha+Q\cos\beta+R\cos\gamma)dS. ∬ΣPdydz+Qdzdx+Rdxdy=∬Σ(Pcosα+Qcosβ+Rcosγ)dS. 其中, cos α , cos β , cos γ \cos\alpha,\cos\beta,\cos\gamma cosα,cosβ,cosγ 为曲面 Σ \varSigma Σ 正侧法向量的方向余弦。
【例】设 f ( x , y , z ) f(x,y,z) f(x,y,z) 为连续函数, Σ \varSigma Σ 为平面 x − y + z − 1 = 0 x-y+z-1=0 x−y+z−1=0 在第四卦限部分的上侧,计算 ∬ Σ [ f ( x , y , z ) + x ] d y d z + [ 2 f ( x , y , z ) + y ] d z d x + [ f ( x , y , z ) + z ] d x d y . \iint_{\varSigma}[f(x,y,z)+x]dydz+[2f(x,y,z)+y]dzdx+[f(x,y,z)+z]dxdy. ∬Σ[f(x,y,z)+x]dydz+[2f(x,y,z)+y]dzdx+[f(x,y,z)+z]dxdy. 解: 平面 Σ \varSigma Σ 如下图所示:

曲面 Σ \varSigma Σ 的法向量为 { 1 , − 1 , 1 } \{1,-1,1\} {1,−1,1} ,对应的方向余弦为 cos α = 1 / 3 , cos β = − 1 / 3 , cos γ = 1 / 3 \cos\alpha=1/\sqrt{3},\cos\beta=-1/\sqrt{3},\cos\gamma=1/\sqrt{3} cosα=1/3,cosβ=−1/3,cosγ=1/3 ,则原积分可化为 ∬ Σ { [ f ( x , y , z ) + x ] / 3 − [ 2 f ( x , y , z ) + y ] / 3 + [ f ( x , y , z ) + z ] / 3 } d S . \iint_{\varSigma}\{[f(x,y,z)+x]/\sqrt{3}-[2f(x,y,z)+y]/\sqrt{3}+[f(x,y,z)+z]/\sqrt{3}\}dS. ∬Σ{[f(x,y,z)+x]/3−[2f(x,y,z)+y]/3+[f(x,y,z)+z]/3}dS. 即 ∬ Σ ( x + z − y ) / 3 d S = S / 3 = ( 1 / 2 × 2 × 2 × 3 / 2 ) / 3 = 1 / 2. \iint_{\varSigma}(x+z-y)/\sqrt{3}dS=S/\sqrt{3}=(1/2\times\sqrt{2}\times\sqrt{2}\times\sqrt{3}/2)/\sqrt{3}=1/2. ∬Σ(x+z−y)/3dS=S/3=(1/2×2×2×3/2)/3=1/2.
三、场论初步
3.1 梯度、旋度、散度
设 u = f ( x , y , z ) u=f(x,y,z) u=f(x,y,z) 可偏导,则 u u u 的梯度为 g r a d u = { ∂ f / ∂ x , ∂ f / ∂ y , ∂ f / ∂ z } \pmb{grad}\space u=\{\partial f/\partial x,\partial f/\partial y,\partial f/\partial z\} grad u={∂f/∂x,∂f/∂y,∂f/∂z} 。这个我们之前接触过,是函数在某点处增长最快的方向。
设向量场 A → = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A={P(x,y,z),Q(x,y,z),R(x,y,z)} ,则 A → \overrightarrow{A} A 的旋度为 r o t A → = ∣ i → j → k → ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ . \pmb{rot}\space\overrightarrow{A}=\begin{vmatrix} \overrightarrow{i} & \overrightarrow{j}& \overrightarrow{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R\end{vmatrix}. rot A= i∂x∂Pj∂y∂Qk∂z∂R . 设向量场 A → = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A={P(x,y,z),Q(x,y,z),R(x,y,z)} ,则 A → \overrightarrow{A} A 的散度为 d i v A → = ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z . div\space \overrightarrow{A}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}. div A=∂x∂P+∂y∂Q+∂z∂R.
应该只会考梯度吧,我看其他两个连例题都没有。
3.2 通量与环流量
1. 通量
设 A → ( x , y , z ) = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A(x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)} 为向量场,其中 P , Q , R P,Q,R P,Q,R 连续可偏导, Σ \varSigma Σ 为有侧曲面,称 Φ = ∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ A → ⋅ n → d S \varPhi=\iint_{\varSigma}Pdydz+Qdzdx+Rdxdy=\iint_{\varSigma}\overrightarrow{A}\cdot\overrightarrow{n}dS Φ=∬ΣPdydz+Qdzdx+Rdxdy=∬ΣA⋅ndS 为向量场 A → \overrightarrow{A} A 指向指定侧的流过有侧曲面 Σ \varSigma Σ 的通量(或流量),其中 n → \overrightarrow{n} n 为曲面 Σ \varSigma Σ 的正侧单位法向量。
好像这个就是两类曲面积分之间的关系 O.O
2. 环流量
设 A → ( x , y , z ) = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A(x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)} 为向量场,其中 P , Q , R P,Q,R P,Q,R 连续可偏导, L L L 为有向闭曲线,称 ∮ L P d x + Q d y + R d z = ∮ L A → ⋅ d s → . \oint_LPdx+Qdy+Rdz=\oint_L\overrightarrow{A}\cdot d\overrightarrow{s}. ∮LPdx+Qdy+Rdz=∮LA⋅ds. 为向量场 A → ( x , y , z ) \overrightarrow{A}(x,y,z) A(x,y,z) 沿有向闭曲线 L L L 的环流量。
写在最后
曲面积分的学习是痛苦的,当然主要还是因为前面的二重、三重、空间解析几何不扎实,不过也顺利处理掉了。
那高等数学理论部分到此就全部结束了,一个漫长的过程,也是三门中分值最大的一部分。剩下的时间里就好好对它进行总结和实践吧。
相关文章:

【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 4. 对坐标的曲面积分(第二类曲面积分)与场论初步
文章目录 二、曲面积分2.2 对坐标的曲面积分(第二类曲面积分)1. 问题产生 —— 流量2. 对坐标的曲面积分的定义(了解)3. 对坐标的曲面积分的性质4. 对坐标的曲面积分的计算法(1) 二重积分法(2&a…...
使用Thrift实现跨语言RPC调用
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
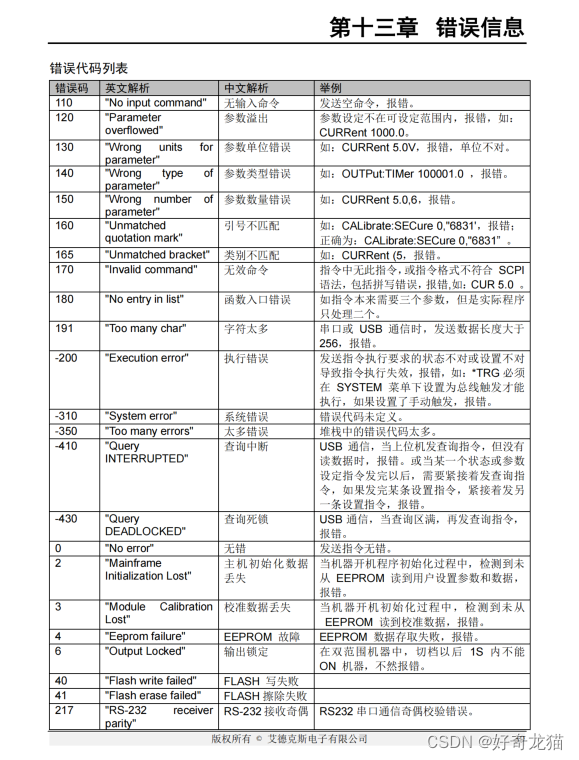
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】 1、前言2、实验环境3、自我总结1、基础了解仪器控制-熟悉仪器2、连接SCPI协议3、选择控制方式-程控方式-RS2324、代码编写 4、熟悉协议-SCPI协议5、测试实验-测试指令(1)硬件连接(…...

leetcode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果…...

Error string: Could not load library
启动Rivz时,报错: Error string: Could not load library (Poco exception libg2o_csparse_extension.so.0.1: cannot open shared object file: No such file or directory) [ERROR] [1696572310.529059051]: Failed to load nodelet [/radar_graph_s…...

pom.xml里的标签
pom.xml 是 Maven 项目的配置文件,其中包含了各种配置信息和依赖管理。下面是一些常见的 pom.xml 中的标签和其作用的简要说明: <project>:根标签,定义了整个项目的基本信息和结构。 <groupId>:指定项目所…...

微服务部署的正确策略
微服务部署挑战 单体应用程序的部署意味着您运行单个(通常是大型应用程序)的多个相同副本。这主要是通过配置 N 个服务器(无论是物理服务器还是虚拟服务器)并在每台服务器上运行应用程序的 M 个实例来完成。虽然这看起来非常简单…...

C#中的数组探究与学习
目录 C#中的数组一般分为:一.数组定义:为什么要使用数组?什么是数组?C#一维数组for和foreach的区别C#多维数组C#锯齿数组初始化的意义:适用场景:C#中的数组一般分为: ①.一维数组。 ②.多维数组,也叫矩形数组。 ③.锯齿数组,也叫交错数组。 一.数组定义: 数组…...

计算机网络八股
1、请你说说TCP和UDP的区别 TCP提供面向连接的可靠传输,UDP提供面向无连接的不可靠传输。UDP在很多实时性要求高的场景有很好的表现,而TCP在要求数据准确、对速度没有硬件要求的场景有很好的表现。TCP和UDP都是传输层协议,都是为应用层程序服…...

Waves 14混音特效插件合集mac/win
Waves14是一款音频处理软件,主要用于音频编辑、混音和母带处理。该软件提供了各种插件,包括EQ、压缩、混响、延迟、失真等,以及一些专业的音频处理工具,如L2限幅器、Linear Phase EQ和多频道扬声器管理。 Mac软件下载:…...
Python python-docx 使用教程
openpyxl是Python下的Word库,它能够很容易的对Word文档进行读取 安装方法:pip install python-docx国内镜像安装:pip install -i https://mirrors.aliyun.com/pypi/simple/ python-docx(推荐,安装更快)中文…...
Mac上protobuf环境构建-java
参考文献 getting-started 官网pb java介绍 maven protobuf插件 简单入门1 简单入门2 1. protoc编译器下载安装 https://github.com/protocolbuffers/protobuf/releases?page10 放入.zshrc中配置环境变量 ~/IdeaProjects/test2/ protoc --version libprotoc 3.12.1 …...
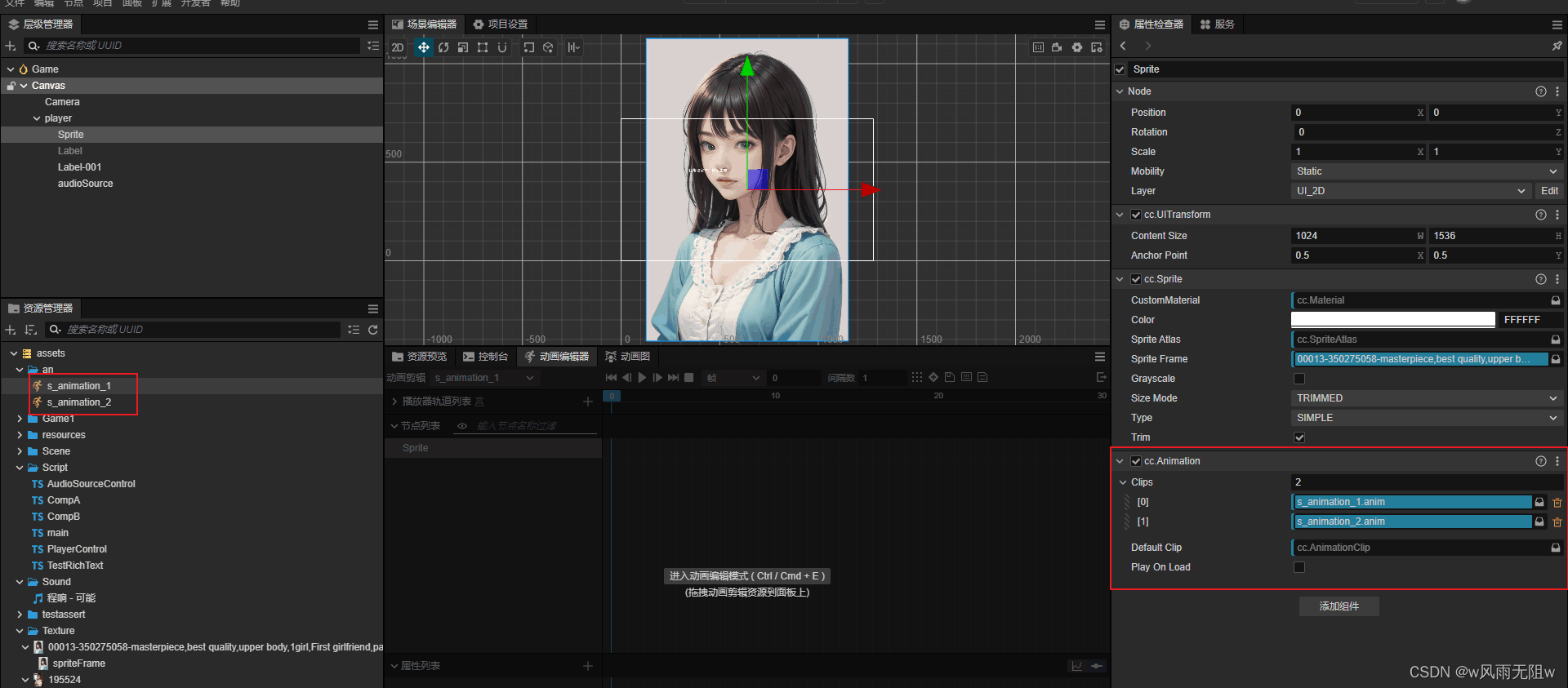
CocosCreator3.8研究笔记(二十二)CocosCreator 动画系统-动画剪辑和动画组件介绍
国庆假期,闲着没事,在家研究技术~ 大家都知道在Cocos Creator3.x 的版本的动画编辑器中,可以实现不用写一行代码就能实现各种动态效果。 Cocos Creator动画编辑器中主要实现关键帧动画,不仅支持位移、旋转、缩放、帧动画ÿ…...

信看课堂-厘米GNSS定位
我们常常说GPS 定位,不过定位远不止GPS定位,通过本节课程,我们将会了解到,原来GPS只是定位的一种: GNSS概述 不同的GNSS系统使用不同的频段来传输导航信号。以下是一些主要的GNSS系统及其相应的频段,用表…...
)
2023CCPC网络赛(A E)
2023CCPC网络赛(A E) The 2nd Universal Cup. Stage 3: Binjiang - Dashboard - Contest - Universal Cup Judging System A. Almost Prefix Concatenation 思路:首先考虑如何求出每个位置允许失配一次的LCP长度 , 可以二分哈希求LCP , 即…...

使用 python 检测泛洪攻击的案例
使用 python 检测泛洪攻击的案例 本案例只使用python标准库通过执行命令来监控异常请求, 并封锁IP, 不涉及其他第三方库工具. import os import time from collections import Counter# 1、update 命令, 采集CPU的平均负载 def get_cpu_load():"""uptime 命令…...

SCROLLINFO scrollInfo; 2023/10/5 下午3:38:53
2023/10/5 下午3:38:53 SCROLLINFO scrollInfo;scrollInfo.cbSize = sizeof(SCROLLINFO);scrollInfo.fMask = SIF_ALL;//scrollInfo.nMin = 0; // 最小位置//scrollInfo.nMax = nRowCountToShow; // 最大位置//scrollInfo.nPage = nRowCountToShow; // 页面大小//scrollInf…...

Python--控制台获取输入与正则表达式
前言一、控制台获取输入1.1 字符串输入1.2 整数输入1.3 浮点数输入1.4 布尔值输入1.5 列表输入1.6 汇总 二、正则表达式2.1 匹配数字2.2 模式检查2.3 替换字符2.4 切分字符串2.5 搜索并提取匹配的部分2.6 使用捕获组提取匹配的部分2.7 非贪婪匹配2.8 忽略大小写匹配2.9 使用预定…...
网络基础知识面试题1
VC++常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C++软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...)...

JavaScript系列从入门到精通系列第十五篇:JavaScript中函数的实参介绍返回值介绍以及函数的立即执行
文章目录 一:函数的参数 1:形参如何定义 2:形参的使用规则 二:函数的返回值 1:函数返回值如何定义 2:函数返回值种类 三:实参的任意性 1:方法可以作为实参 2:将匿…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
