7.Tensors For Beginneers - Convector Components
介绍协向量时,曾说过它们有点像 行向量, 行向量确实以某种方式代表了协向量,
这里说明一下:
协向量是不变的; 协向量组件是可变的。

协向量不依赖坐标系,协向量的组件取决于坐标系。
当我们说协向量具有组件时,我们的意思是?

要记住:协向量是 一个 从向量到实数的函数,协向量并不存在向量空间V中,协向量只是将V中的向量作为输入,所以我们不能使用V中的基向量来构造协向量,
所以应该怎么做才对?

从V中取两基向量,并引入两个协向量(从向量到实数的函数),
并定义它们的计算结果,
如图: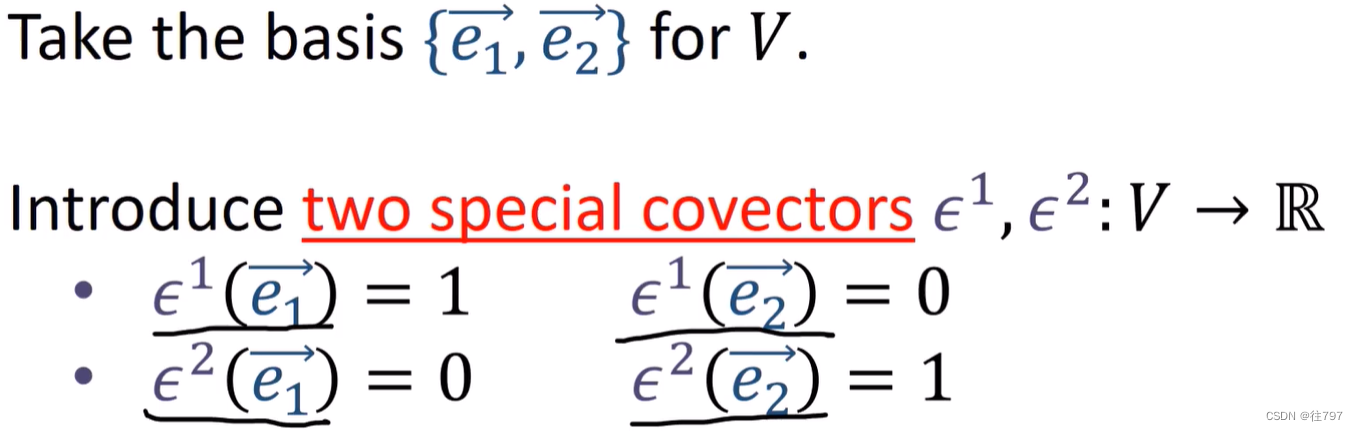
还记得那个 kronecker Delta 吗。
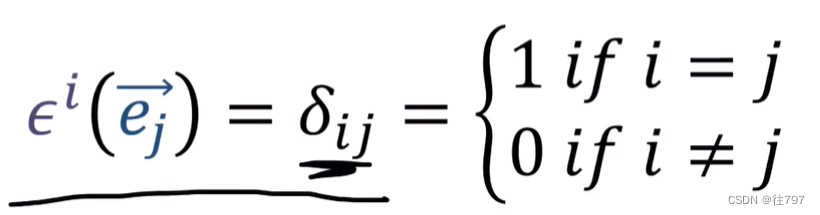
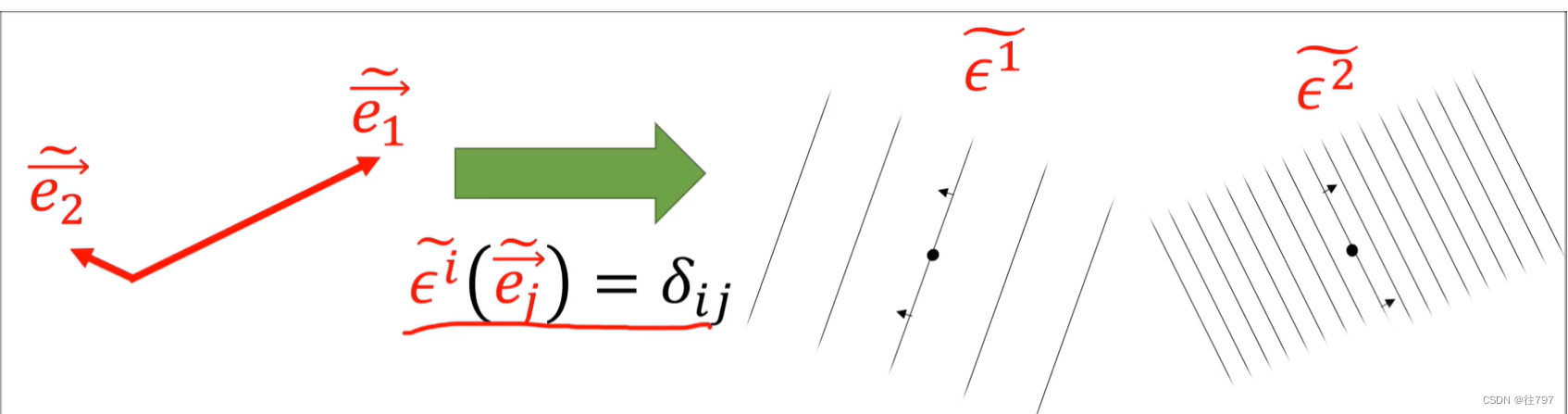
这些协向量 实际上看起来像一堆线吗? 为找到答案,把它们作用到某个向量v上,
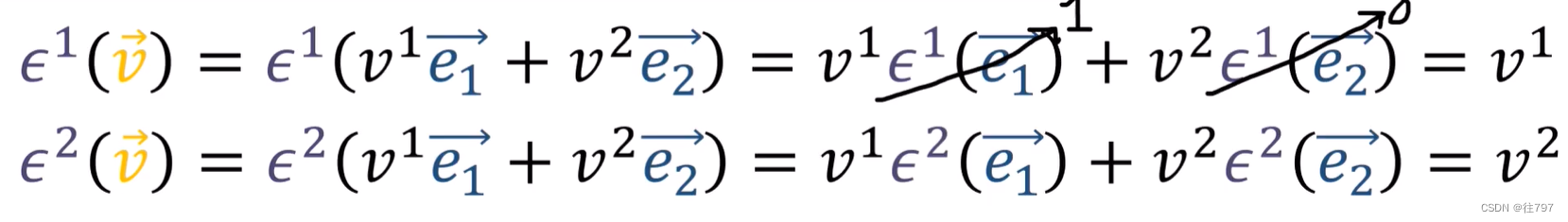
仔细 看,这些 所做的是:它们在投射矢量分量,是把?
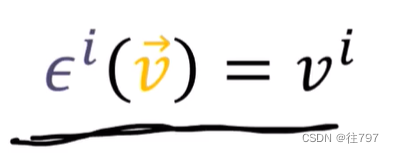
当把应用到v中,我们将得到v基向量e1、e2上的组件,
所以,看起来就像是:可以帮助我们获得向量v的第一个分量,其中e1就是指向这个分量的方向。
看起来就像是:可以帮助我们获得向量v的第2个分量,其中e2就是指向这个分量的方向。
这就是协向量的样子(视觉上)

现在我们对向量v应用一些通用的协向量α,α可以是任一协向量
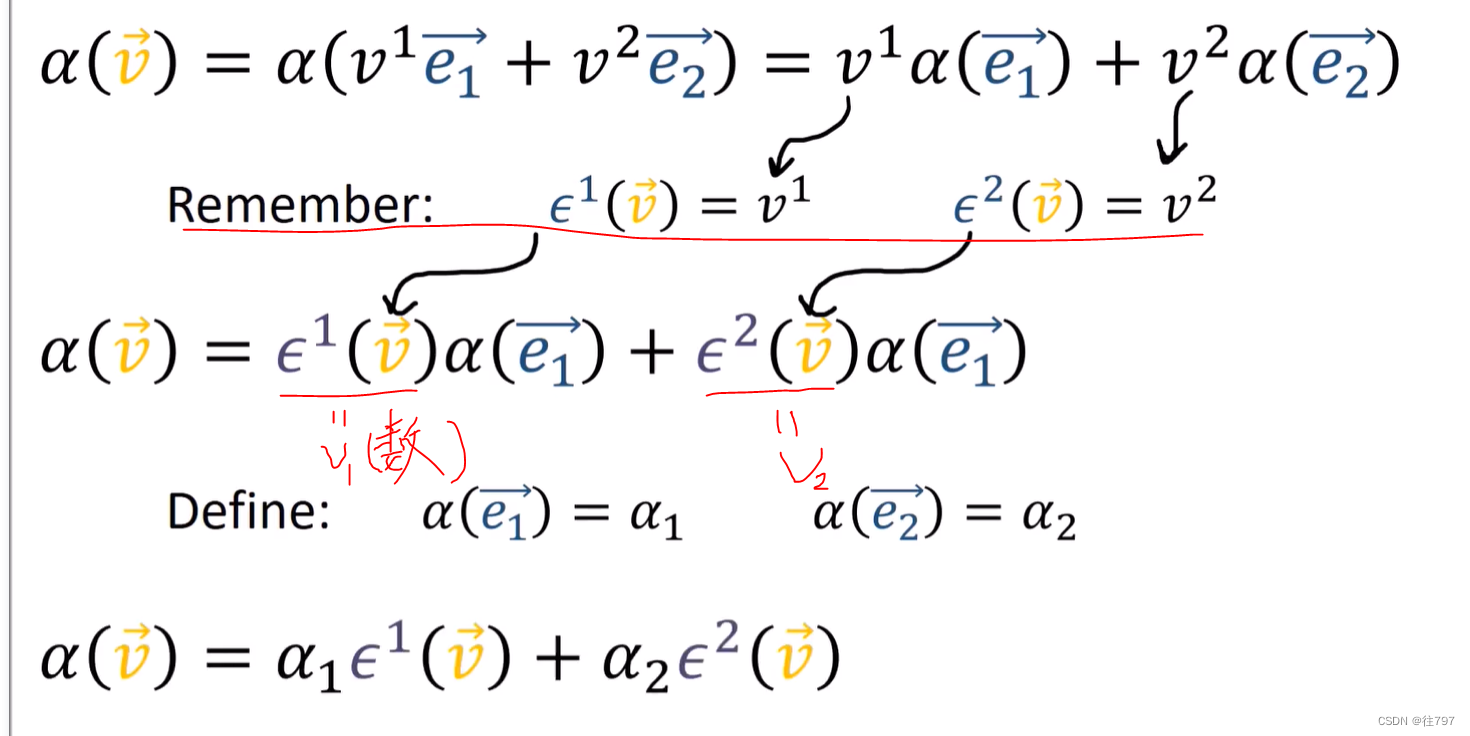
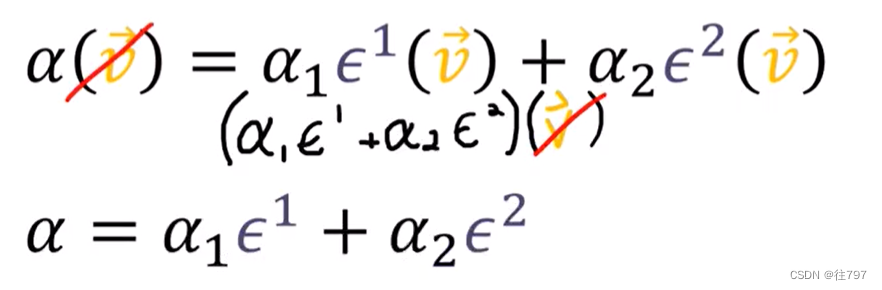
(注:α1=α*e1=一个数,α2也是一个数,上面表示 任意一个协向量α = 数1* + 数2*
)
所以上面我们所作的是:编写了一个通用的协向量α(α可以是任意协向量) 作为协向量的线性组合,
所以这意味着协向量 是 构成了所有协向量集合的基底,
也因为这个原因,被称为 ”对偶基“ , 因为它们是对偶空间V* 上的 基底。
以上我们就用了代数的方式写出了 一个协向量的表达,
现考虑视觉上,
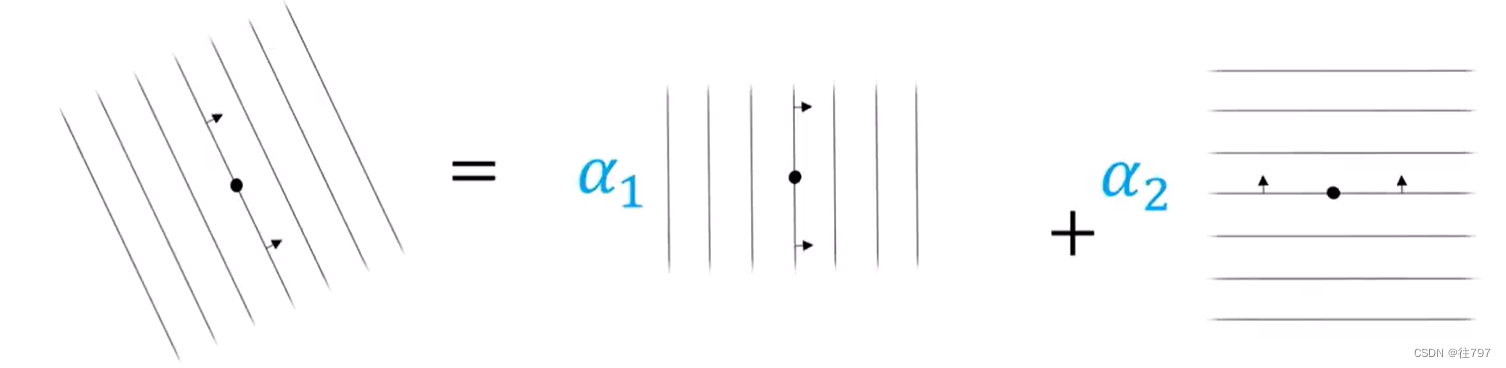
假设有一个协向量α,一簇在e1、e2为基底的向量空间的线, 可通过把α应用到基底e1、e2上来获得α的组件,只需计算穿透的行数,
我们可以把α写成、
的线性组合 的方式来表示α。
所以过程就是:从基底向量开始,使用这个定义 来获得对偶协向量的基底,然后使用 这些 我们就可以将任意的协向量表示为对偶基的线性组合。(这是对上面整个过程的描述)
但记住,、
并不是 唯一的基底,(正如向量空间那般,基底可以变,基底个数不变那般)
因此,我们可以用别的向量开始,如:
并使用以下规则,我们可以定义另一对对偶基,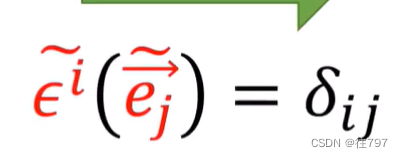 (规则--就是规定)
(规则--就是规定)
同样地,可将任意协向量α表示为 、
的线性组合。

例子:
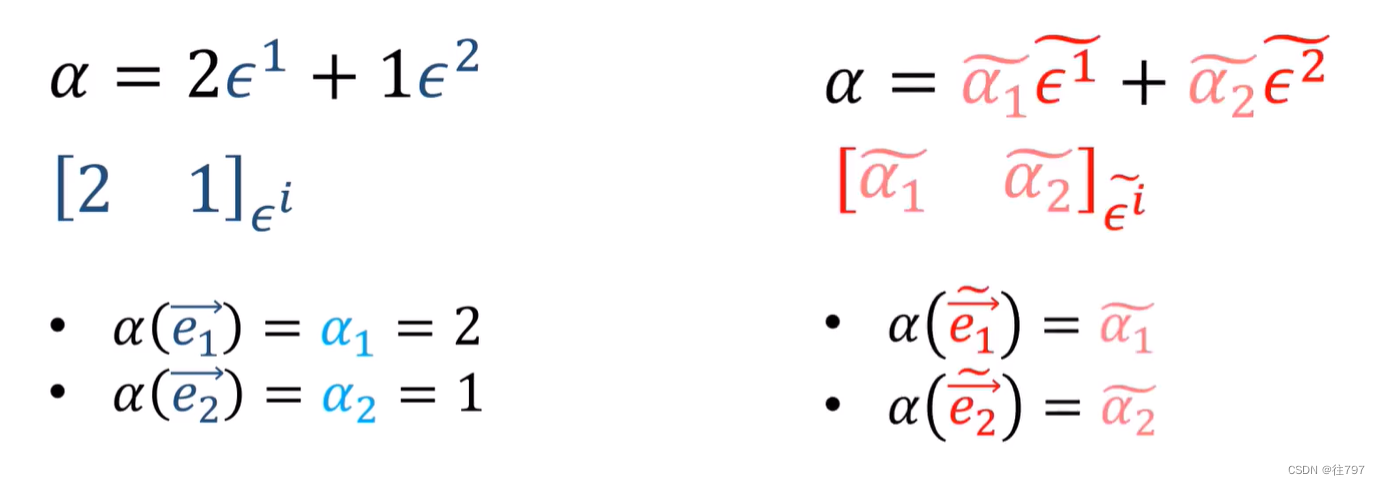
已知一个协向量α在 旧(对偶)基、
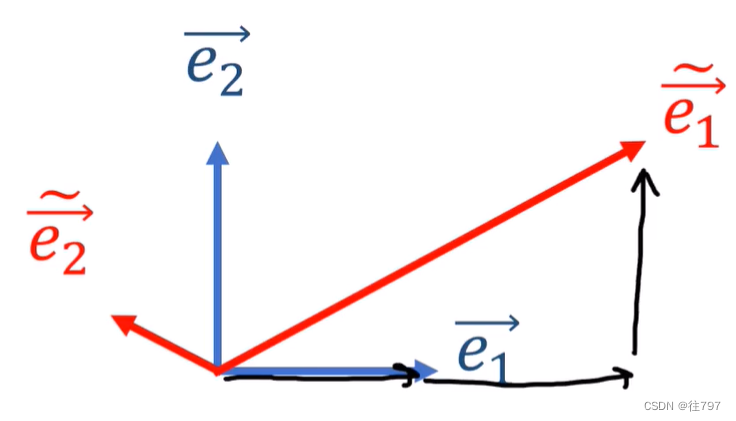
下的线性表示, 同时有一对新(对偶)基
、
,想把协向量α利用新基
、
做线性表示,
将α应用到新基底,
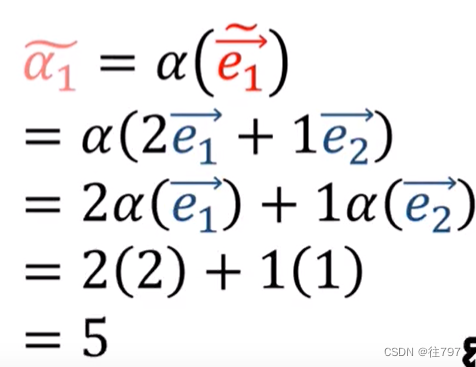
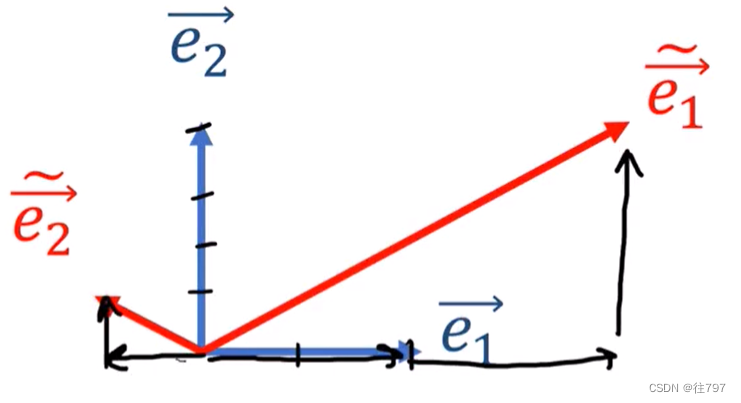
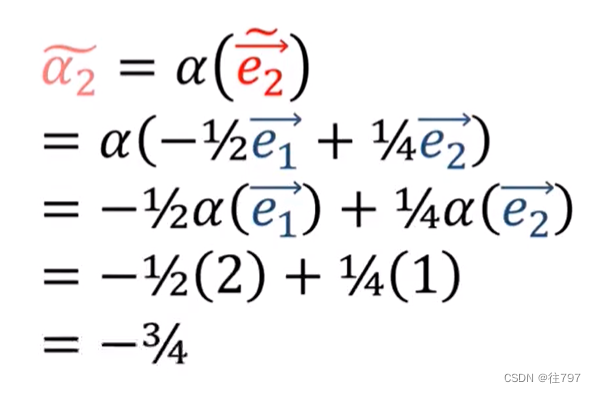
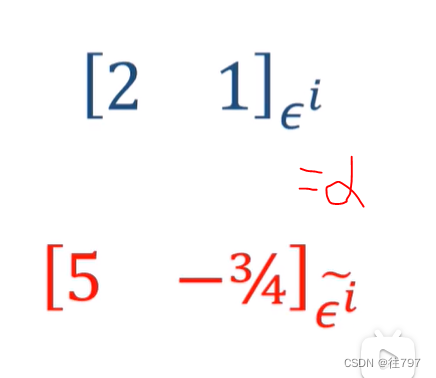
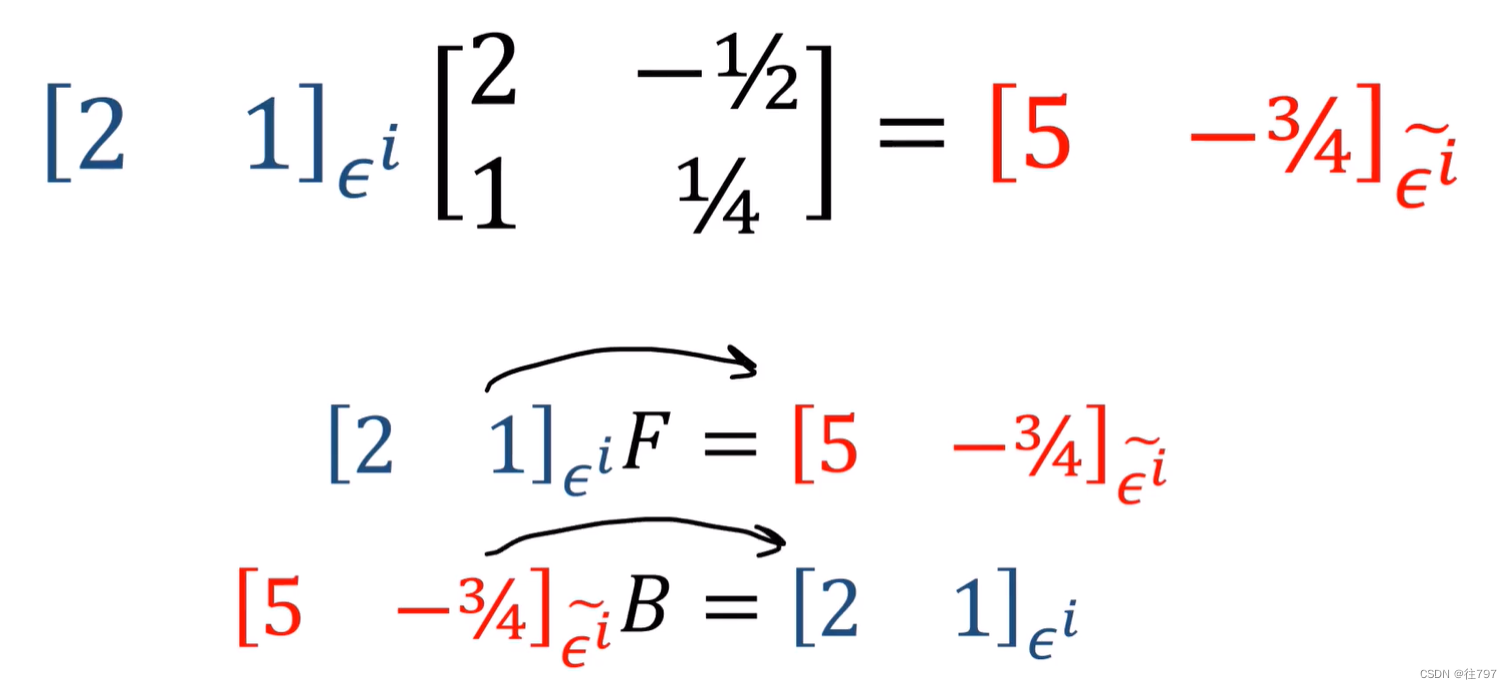
以上是向量的转换;
以下是基底的转换;
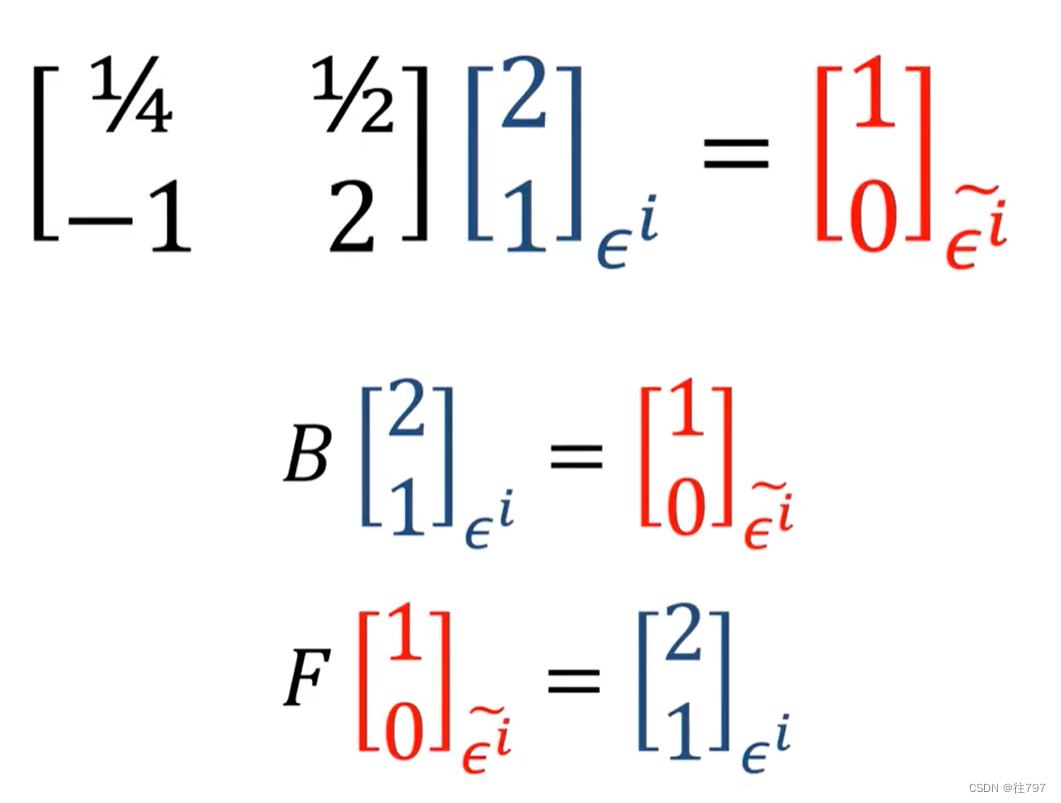
仔细观察,协向量中:基底的转换: 旧基到新基---用B,新基到旧基===用F;
这与向量的完全相反!
协向量中:某个协向量的转换:利用旧基到利用新基---用F,利用新基到利用旧基--用B
这与向量的完全相反!
这就是为什么不能只翻转列向量来获得行向量,--------这在正交基上有效,
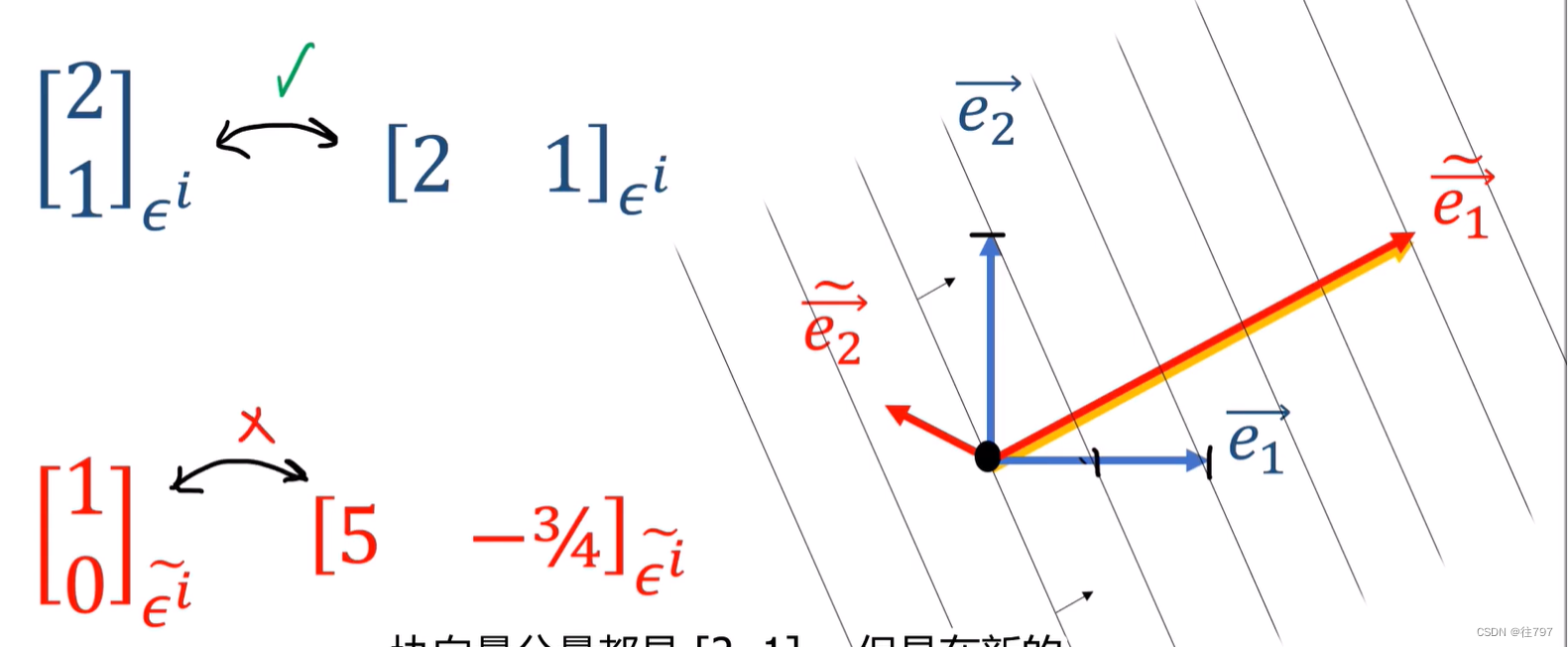
你看上图, 对于利用正交基, 协向量你把它从列向量转置成行向量,2,1仍是2,1;
但是,一旦不是正交基了, 【1;0】变为 【5,-3/4】明显不能靠转置来获得。
所以,向量分量是通过计算构建向量时使用了多少基向量来测量的,
但是协向量分量是通过计算 基向量 穿过的协向量线的数量来测量的。
相关文章:

7.Tensors For Beginneers - Convector Components
介绍协向量时,曾说过它们有点像 行向量, 行向量确实以某种方式代表了协向量, 这里说明一下: 协向量是不变的; 协向量组件是可变的。 协向量不依赖坐标系,协向量的组件取决于坐标系。 当我们说协向量具有组…...

直线导轨坏了可以维修吗?
直线导轨是工业自动化设备中常用的零部件,其性能和使用寿命对设备的稳定运行和产能有着直接的影响,在生产中,由于各种原因,直线导轨会出现各种问题,那么,直线导轨的维修方法究竟是怎样的呢?我们…...

Java基础--泛型详解
一、背景 java推出泛型之前,集合元素类型可以是object类型,能够存储任意的数据类型对象,但是在使用过程中,如果不知道集合里面的各个元素的类型,在进行类型转换的时候就很容易引发ClassCastException异常。 二、概念 …...
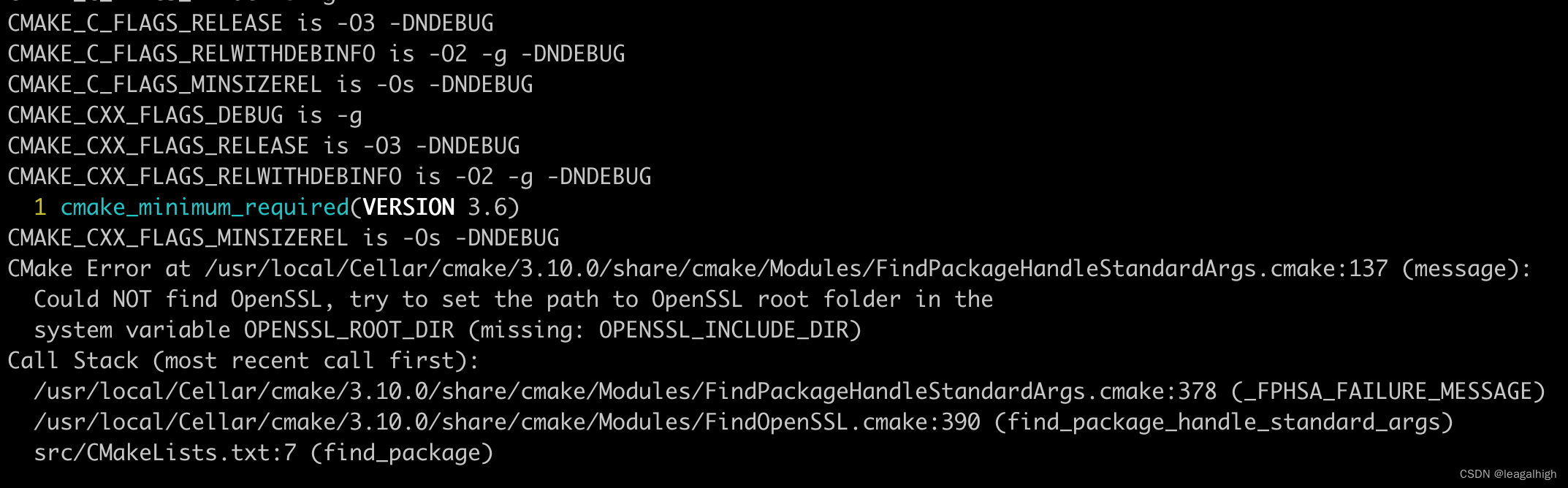
学习搜狗的workflow,MacBook上如何编译
官网说可以在MacBook上也可以运行,但是编译的时候却有找不到openssl的错误: 看其他博客也有类似的错误,按照类似的思路去解决 问题原因和解决办法 cmake编译的时候,没有找到openssl的头文件,需要设置cmake编译环境下…...
Ubuntu使用cmake和vscode开发自己的项目,引用自己的头文件和openCV
创建文件夹 mkdir my_proj 继续创建include 和 src文件夹,形成如下的目录结构 用vscode打开项目 创建add.h #ifndef ADD_H #define ADD_Hint add(int numA, int numB);#endif add.cpp #include "add.h"int add(int numA, int numB) {return numA nu…...
 dataset, dataloader)
2) dataset, dataloader
dataset, dataloader torchvision.datasets里面集成了一些常见的数据集,例如MNIST和CIFAR10 1) Dataset 以MNIST为例,其使用方式如下 import torch import torchvision from torchvision import transformstrain_dataset = torchvision.datasets.MNIST(root=../data,trai…...

阿里云PolarDB自研数据库详细介绍_兼容MySQL、PostgreSQL和Oracle语法
阿里云PolarDB数据库是阿里巴巴自研的关系型分布式云原生数据库,PolarDB兼容三种数据库引擎:MySQL、PostgreSQL、Oracle(语法兼容),目前提供云原生数据库PolarDB MySQL版、云原生数据库PolarDB PostgreSQL版和云原生数…...
[软件工具]opencv-svm快速训练助手教程解决opencv C++ SVM模型训练与分类实现任务支持C# python调用
opencv中已经提供了svm算法可以对图像实现多分类,使用svm算法对图像分类的任务多用于场景简单且对时间有要求的场景,因为opencv的svm训练一般只需要很短时间就可以完成训练任务。但是目前网上没有一个工具很好解决训练问题,大部分需要自己编程…...
邮件注册(一)验证码发送
通过邮箱实现注册,用户请求验证码完成注册操作。 导入依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId></dependency><dependency><g…...
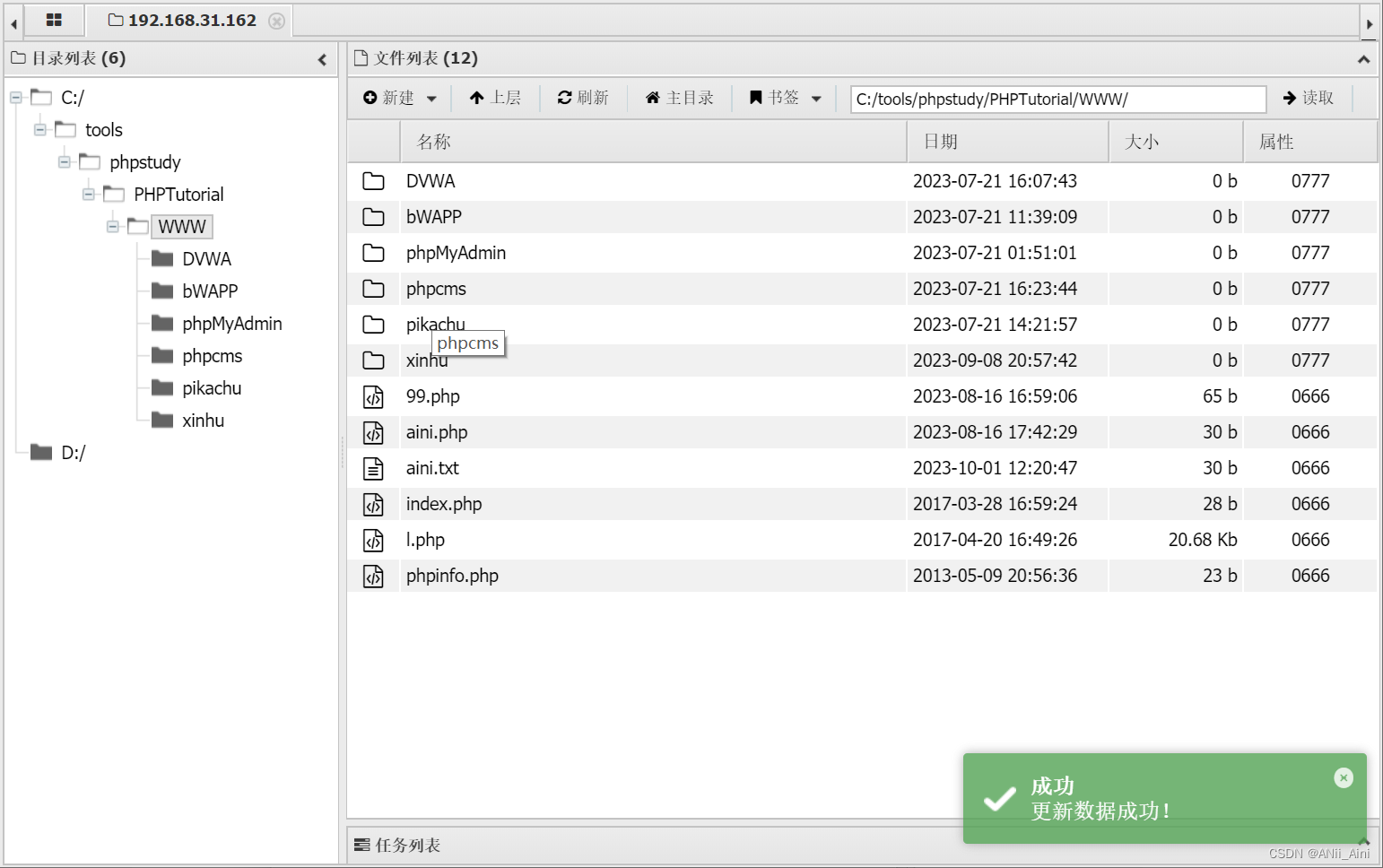
【网络安全---sql注入(2)】如何通过SQL注入getshell?如何通过SQL注入读取文件或者数据库数据?一篇文章告诉你过程和原理。
前言 本篇博客主要是通过piakchu靶场来讲解如何通过SQL注入漏洞来写入文件,读取文件。通过SQL输入来注入木马来getshell等,讲解了比较详细的过程; 如果想要学习SQL注入原理以及如何进行SQL注入,我也写了一篇详细的SQL注入方法及…...
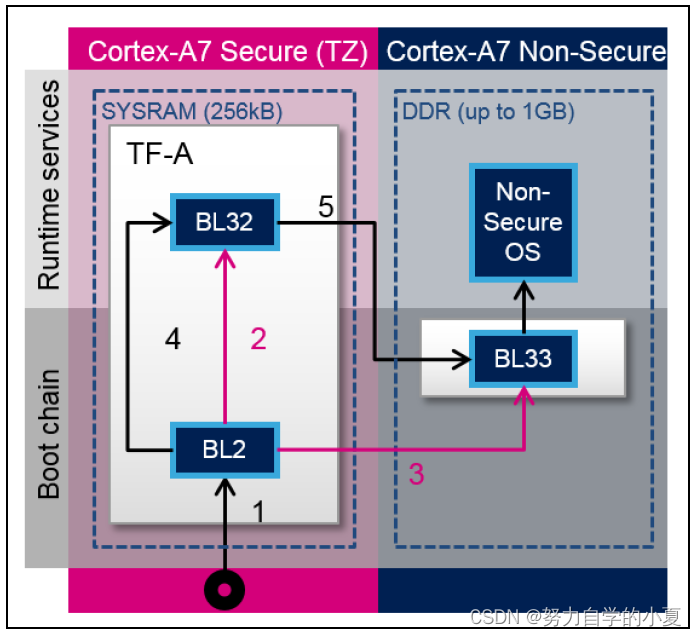
正点原子嵌入式linux驱动开发——TF-A移植
经过了之前的学习,除了TF-A的详细启动流程仍待更新,TF-A的使用和其对应的大致启动流程已经进行过了学习。但是当我们实际做产品时,硬件平台肯定会和ST官方的有区别,比如DDR容量会改变,自己的硬件没有使用到官方EVK开发…...
GB28181学习(六)——实时视音频点播(数据传输部分)
GB28181系列文章: 总述:https://blog.csdn.net/www_dong/article/details/132515446 注册与注销:https://blog.csdn.net/www_dong/article/details/132654525 心跳保活:https://blog.csdn.net/www_dong/article/details/132796…...
JMeter接口自动化测试(数据驱动)
之前我们的用例数据都是配置在HTTP请求中,每次需要增加,修改用例都需要打开JMeter重新编辑,当用例越来越多的时候,用例维护起来就越来越麻烦,有没有好的方法来解决这种情况呢?我们可以将用例的数据存放在cs…...

数据结构:二叉树(超详解析)
目录 1.树概念及结构 1.1树的概念 1.2树的相关概念 1.3树的表示 1.3.1孩子兄弟表示法: 1.3.2双亲表示法:只存储双亲的下标或指针 两节点不在同一树上: 2.二叉树概念及结构 2.1.概念 2.2.特殊的二叉树: 2…...

【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 4. 对坐标的曲面积分(第二类曲面积分)与场论初步
文章目录 二、曲面积分2.2 对坐标的曲面积分(第二类曲面积分)1. 问题产生 —— 流量2. 对坐标的曲面积分的定义(了解)3. 对坐标的曲面积分的性质4. 对坐标的曲面积分的计算法(1) 二重积分法(2&a…...
使用Thrift实现跨语言RPC调用
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
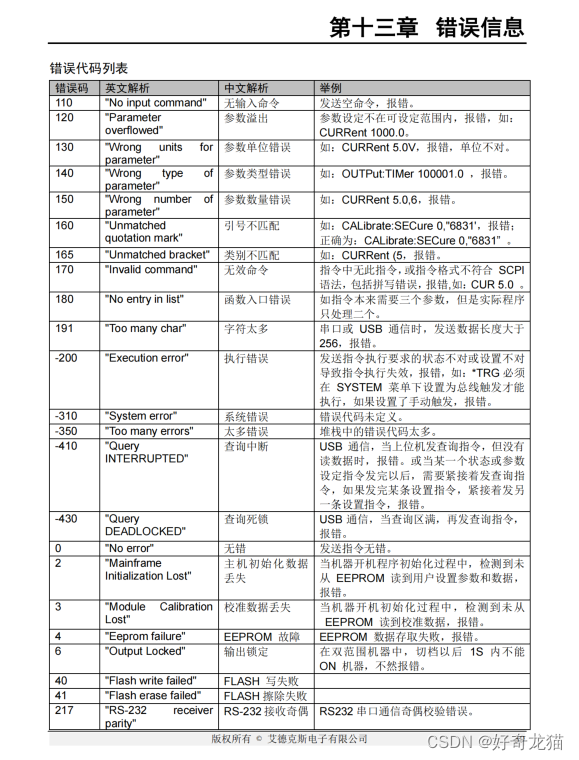
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】 1、前言2、实验环境3、自我总结1、基础了解仪器控制-熟悉仪器2、连接SCPI协议3、选择控制方式-程控方式-RS2324、代码编写 4、熟悉协议-SCPI协议5、测试实验-测试指令(1)硬件连接(…...

leetcode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果…...

Error string: Could not load library
启动Rivz时,报错: Error string: Could not load library (Poco exception libg2o_csparse_extension.so.0.1: cannot open shared object file: No such file or directory) [ERROR] [1696572310.529059051]: Failed to load nodelet [/radar_graph_s…...

pom.xml里的标签
pom.xml 是 Maven 项目的配置文件,其中包含了各种配置信息和依赖管理。下面是一些常见的 pom.xml 中的标签和其作用的简要说明: <project>:根标签,定义了整个项目的基本信息和结构。 <groupId>:指定项目所…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
