数据结构:二叉树(超详解析)
目录
1.树概念及结构
1.1树的概念
1.2树的相关概念
1.3树的表示
1.3.1孩子兄弟表示法:
1.3.2双亲表示法:只存储双亲的下标或指针
两节点不在同一树上:
2.二叉树概念及结构
2.1.概念
2.2.特殊的二叉树:
2.2.1.满二叉树:
编辑2.2.2. 完全二叉树:h = (log2(N+1))
2.3.二叉树的性质
2.4.二叉树的存储结构
2.4.1. 顺序存储:
2.4.2.链式存储:
3.二叉树的顺序结构及实现
3.1.二叉树的顺序结构
3.2.堆的概念及结构
3.3堆的实现
3.4.堆排序
3.5.TOP--K问题
4.二叉树的链式结构及实现
4.1.前序、中序以及后序遍历
4.2层序遍历
以上就是个人学习线性表的个人见解和学习的解析,欢迎各位大佬在评论区探讨!
感谢大佬们的一键三连! 感谢大佬们的一键三连! 感谢大佬们的一键三连!
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
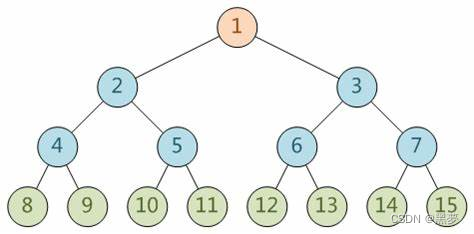
1.1.1.有一个特殊的结点,称为根结点,根节点没有前驱结点;
1.1.2.除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继 ;1.1.3.因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构。
1.2树的相关概念
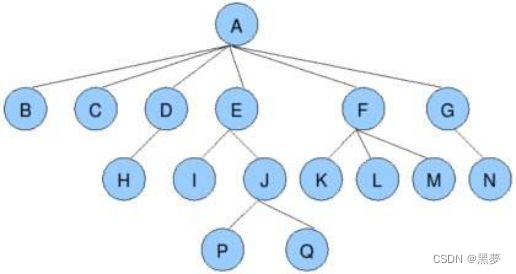
重点重点重点:
1.2.1.节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6。。
1.2.2.叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点。
1.2.3.非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点。
1.2.4.双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点。1.2.5.孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点。
1.2.6.兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点。
1.2.7.树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6。
1.2.8.节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
1.2.9.树的高度或深度:树中节点的最大层次; 如上图:树的高度为4。
1.2.10.堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点。
1.2.11.节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先。
1.2.12.子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙。
1.2.13.森林:由m(m>0)棵互不相交的树的集合称为森林。
1.3树的表示
既要保存值域,也要保存结点和结点之间的关系。
实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。
1.3.1孩子兄弟表示法:
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

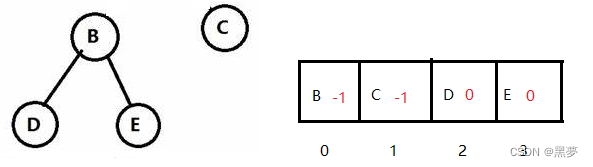
1.3.2双亲表示法:只存储双亲的下标或指针

两节点不在同一树上:
2.二叉树概念及结构
2.1.概念
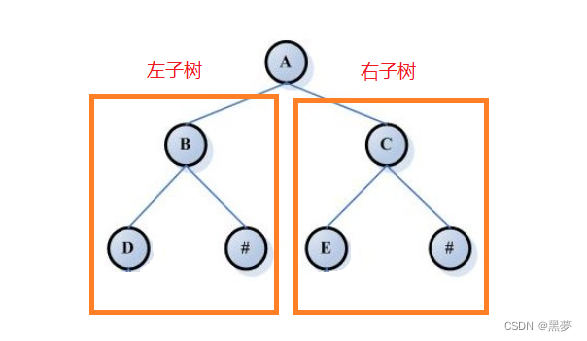
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空 ;
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成 。
注意:
1. 二叉树不存在度大于2的结点;
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
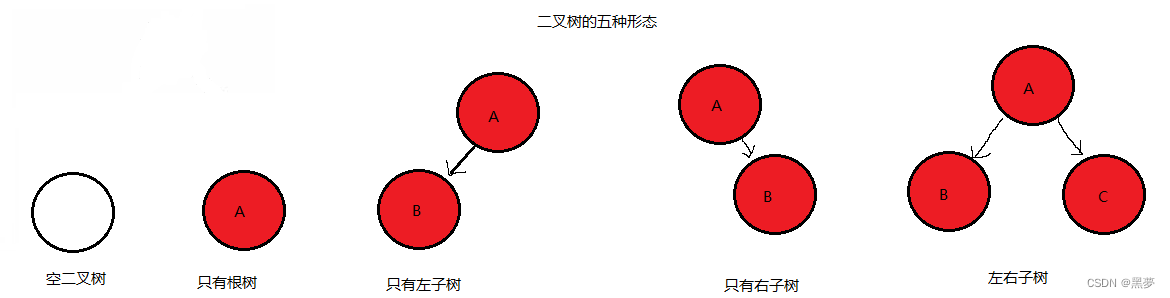
2.2.特殊的二叉树:
2.2.1.满二叉树:
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 2^k-1,则它就是满二叉树。
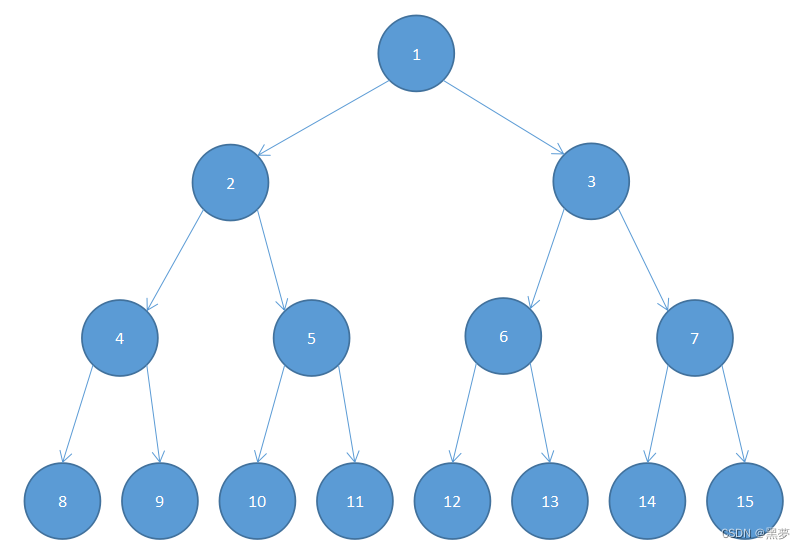
2.2.2. 完全二叉树:h = (log2(N+1))
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
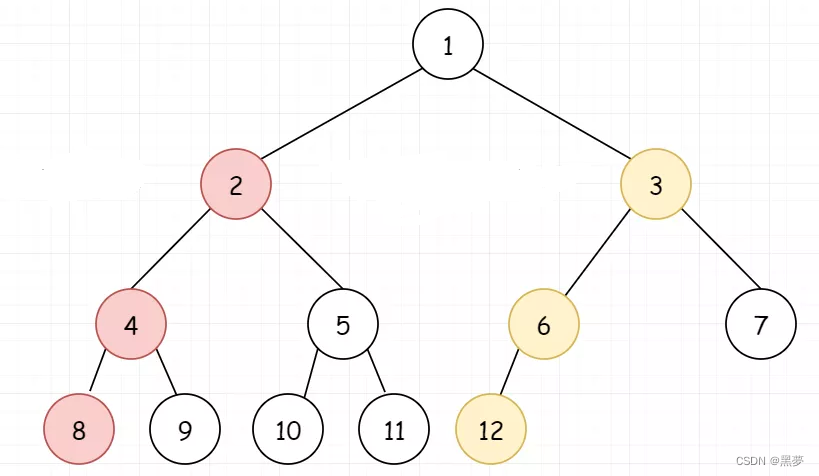
2.3.二叉树的性质
2.3.1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点;
2.3.2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1;
2.3.3. 对任何一棵二叉树, 如果度为n0其叶结点个数为 , 度为2的分支结点个数为n2 ,则有 n0=n2 +1;
2.3.4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log(n+1). (ps:log2(n+1)是log以2 为底,n+1为对数);
2.3.5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点;
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子;
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子;
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A .不存在这样的二叉树
B.200
C. 198
D. 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A. n
B. n+1
C. n-1
D. n/2解析:
0个节点N0,1个节点N1,2个节点N2;2n = N0+N1+N2;2n = N0+N1+N0-1;所以2N0=2n。
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A. 11
B. 10
C. 8
D. 12
4.一个具有767个节点的完全二叉树,其叶子节点个数为()
A. 383
B. 384
C. 385
D. 386解析:
0个节点N0,1个节点N1,2个节点N2;767 = N0+N1+N0-1;2N0 = 768.
2.4.二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
2.4.1. 顺序存储:
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费(当节点无子节点时,数组位置空缺)。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储结构在物理上是一个数组,在逻辑结构上是一颗二叉树。

2.4.2.链式存储:
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,学到高阶数据结构时如红黑树等会用到三叉链。

3.二叉树的顺序结构及实现
3.1.二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2.堆的概念及结构
3.2.1.概念:
如果有一个关键码的集合K = {k1,k2 ,k3,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:ki<=k2i+1 且ki<=k2i+2 (ki>=k2i+1且ki>=k2i+2) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
3.2.2堆的性质:
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。

底层逻辑:
1.物理结构——>数组;
2.逻辑结构——>完全二叉树;
堆:非线性结构,是完全二叉树;
小堆:树中任意一个父亲都<=孩子;
大堆:树中任意一个父亲都>=孩子;
一般解决的问题:
1.topk问题:找前多少个最大值或最小值;
2.堆排序:(时间复杂度O(N*logN)) 冒泡排序(O(N^2))
需要排序100W个元素,堆排序2000W次,冒泡排序1万亿次。
堆的规律:
leftchild = parent*2+1;
rightchild = parent*2+2;
partent = (child-1)/2;
总结:
顺序存储不适合用数组存储;
满二叉树和完全二叉树适合用数组存储。
3.3堆的实现
堆的头文件:
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
//初始化
void HeapInit(HP* php);
void HeapInitArray(HP* php,int* a,int n);//销毁
void HeapDestory(HP* php);//插入
void HeapPush(HP* php, HPDataType x);//弹出
void HeapPop(HP* php);//打印
void HeapPrint(HP* php);//堆顶
HPDataType HeapTop(HP* php);//判断为空
bool HeapEmpty(HP* php);//交换
void Swap(HPDataType* s1, HPDataType* s2);//向上调整
void Adjustup(HPDataType* a, int child);//向下调整
void Adjustdown(HPDataType* a, int n, int parent);
//初始化(为空)111方法一
void HeapInit(HP* php)
{
assert(php);php->size = php->capacity = 0;
php->a = NULL;
}//初始化(不为空不需要再Push)222方法二
void HeapInitArray(HP* php, int* a, int n)
{
assert(php);
assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
perror("malloc fail");
exit(-1);
}php->size = php->capacity = n;
memcpy(php->a, a, n * sizeof(HPDataType));//建堆
for (int i = 1; i < n; i++)
{
Adjustup(php->a, i);
}
}
向上调整:将儿子节点的下标传递给形参,找到父节点,子节点的值与父节点比较,如果子节点比父亲节点大那么进行交换(建大堆),依次循环判断,遍历结束则说明已经完成大堆的创建。
//交换
void Swap(HPDataType* s1, HPDataType* s2)
{
HPDataType tmp = *s1;
*s1 = *s2;
*s2 = tmp;
}//向上调整(此时建立大堆)
void Adjustup(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
向下调整:将父亲节点的下标传递给形参,找到儿子点,子节点的值与父节点比较,如果子节点比父亲节点大那么进行交换(建小堆),依次循环判断,遍历结束则说明已经完成小堆的创建。
//交换
void Swap(HPDataType* s1, HPDataType* s2)
{
HPDataType tmp = *s1;
*s1 = *s2;
*s2 = tmp;
}//向下调整(此时建立小堆)
void Adjustdown(HPDataType* a, int n, int parent)
{
int child = (parent * 2) + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
if (a[parent] > a[child])
{
Swap(&a[child], &a[parent]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;
}
}}
//插入
void HeapPush(HP* php, HPDataType x)
{
assert(php);if (php->size == php->capacity)
{
int newcapacity = php->size == 0 ? 4 : 2 * php->size;
HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}php->capacity = newcapacity;
php->a = tmp;
}php->a[php->size] = x;
php->size++;Adjustup(php->a, php->size-1);
}
//弹出/删除
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);Swap( &php->a[0], &php->a[php->size - 1]);
--php->size;Adjustdown(php->a, php->size, 0);
}
//打印
void HeapPrint(HP* php)
{
assert(php);for(int i = 0;i < php->size;i++)
{
printf("%d ",php->a[i]);
}
printf("\n");
}
//销毁
void HeapDestory(HP* php)
{
assert(php);free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
//堆顶
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);return php->a[0];
}
//判断为空
bool HeapEmpty(HP* php)
{
assert(php);return php->size == 0;
}
3.4.堆排序
升序:建大堆;将最大值和最后一个值交换,然后size-1,一直到size为1时,完成升序排序
降序:建小堆;将最小值和最后一个值交换,然后size-1,一直到size为1时,完成降序排序
3.5.TOP--K问题
即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆;
前k个最小的元素,则建大堆;
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
4.二叉树的链式结构及实现
4.1.前序、中序以及后序遍历
二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。(根,左,右)
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。(左,根,右)
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。(左,右,根)
//前序
void FrontOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->val);FrontOrder(root->left);FrontOrder(root->right);
}//中序
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}//后序
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
4.2层序遍历
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
//结构体
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
int val;
}BTNode;//节点个数
int TreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子节点的个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//第k层的节点数
int TreeKlevel(BTNode* root, int k)
{
assert(k > 0);if (root == NULL)
{
return 0;
}if (k == 1)
{
return 1;
}return TreeKlevel(root->left, k - 1) + TreeKlevel(root->right, k - 1);
}
//查找值为x的节点
BTNode* FindTree(BTNode* root, int x)
{
if (root == NULL)
return NULL;if (root->val == x)
{
return root;
}BTNode* ret = NULL;
ret = FindTree(root->left, x);
if (ret != NULL)
{
return ret;
}
ret = FindTree(root->right, x);
return ret;
}
//层序遍历
void LevelOrder(BTNode* root)
{
Que q;
QueueInit(&q);if (root)
{
QueuePush(&q, root);
}while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->val);
if(front->left != NULL)
QueuePush(&q, front->left);
if(front->right != NULL)
QueuePush(&q, front->right);QueuePop(&q);
}
printf("\n");
}
//判断是否是完全二叉树
int TreeComplete(BTNode* root)
{
Que q;
QueueInit(&q);if (root)
{
QueuePush(&q, root);
}while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);QueuePop(&q);
}
//当在队列中遇到NULL时,判断后面是否有非空节点,有则不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
//销毁
void DestroyTree(BTNode* root)
{
if (root == NULL)
{
return;
}DestroyTree(root->left);
DestroyTree(root->right);free(root);
}
以上就是个人学习线性表的个人见解和学习的解析,欢迎各位大佬在评论区探讨!
感谢大佬们的一键三连! 感谢大佬们的一键三连! 感谢大佬们的一键三连!

相关文章:

数据结构:二叉树(超详解析)
目录 1.树概念及结构 1.1树的概念 1.2树的相关概念 1.3树的表示 1.3.1孩子兄弟表示法: 1.3.2双亲表示法:只存储双亲的下标或指针 两节点不在同一树上: 2.二叉树概念及结构 2.1.概念 2.2.特殊的二叉树: 2…...

【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 4. 对坐标的曲面积分(第二类曲面积分)与场论初步
文章目录 二、曲面积分2.2 对坐标的曲面积分(第二类曲面积分)1. 问题产生 —— 流量2. 对坐标的曲面积分的定义(了解)3. 对坐标的曲面积分的性质4. 对坐标的曲面积分的计算法(1) 二重积分法(2&a…...
使用Thrift实现跨语言RPC调用
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
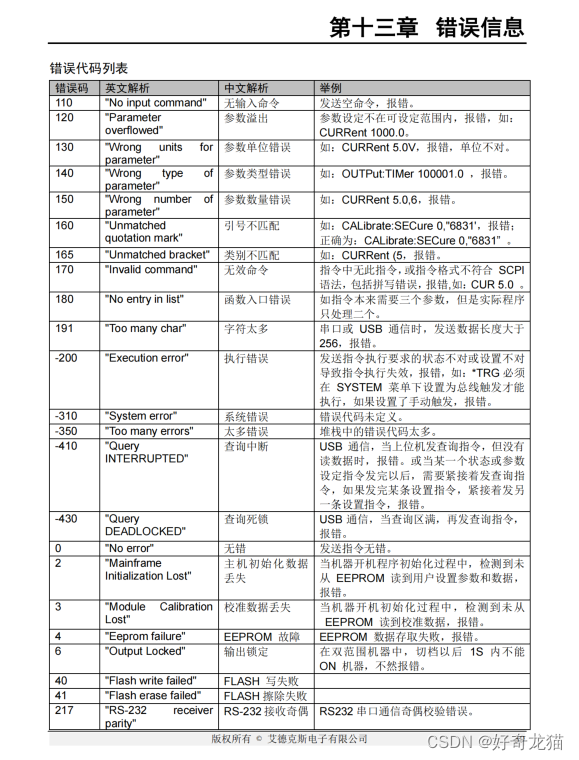
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】 1、前言2、实验环境3、自我总结1、基础了解仪器控制-熟悉仪器2、连接SCPI协议3、选择控制方式-程控方式-RS2324、代码编写 4、熟悉协议-SCPI协议5、测试实验-测试指令(1)硬件连接(…...

leetcode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果…...

Error string: Could not load library
启动Rivz时,报错: Error string: Could not load library (Poco exception libg2o_csparse_extension.so.0.1: cannot open shared object file: No such file or directory) [ERROR] [1696572310.529059051]: Failed to load nodelet [/radar_graph_s…...

pom.xml里的标签
pom.xml 是 Maven 项目的配置文件,其中包含了各种配置信息和依赖管理。下面是一些常见的 pom.xml 中的标签和其作用的简要说明: <project>:根标签,定义了整个项目的基本信息和结构。 <groupId>:指定项目所…...

微服务部署的正确策略
微服务部署挑战 单体应用程序的部署意味着您运行单个(通常是大型应用程序)的多个相同副本。这主要是通过配置 N 个服务器(无论是物理服务器还是虚拟服务器)并在每台服务器上运行应用程序的 M 个实例来完成。虽然这看起来非常简单…...

C#中的数组探究与学习
目录 C#中的数组一般分为:一.数组定义:为什么要使用数组?什么是数组?C#一维数组for和foreach的区别C#多维数组C#锯齿数组初始化的意义:适用场景:C#中的数组一般分为: ①.一维数组。 ②.多维数组,也叫矩形数组。 ③.锯齿数组,也叫交错数组。 一.数组定义: 数组…...

计算机网络八股
1、请你说说TCP和UDP的区别 TCP提供面向连接的可靠传输,UDP提供面向无连接的不可靠传输。UDP在很多实时性要求高的场景有很好的表现,而TCP在要求数据准确、对速度没有硬件要求的场景有很好的表现。TCP和UDP都是传输层协议,都是为应用层程序服…...

Waves 14混音特效插件合集mac/win
Waves14是一款音频处理软件,主要用于音频编辑、混音和母带处理。该软件提供了各种插件,包括EQ、压缩、混响、延迟、失真等,以及一些专业的音频处理工具,如L2限幅器、Linear Phase EQ和多频道扬声器管理。 Mac软件下载:…...
Python python-docx 使用教程
openpyxl是Python下的Word库,它能够很容易的对Word文档进行读取 安装方法:pip install python-docx国内镜像安装:pip install -i https://mirrors.aliyun.com/pypi/simple/ python-docx(推荐,安装更快)中文…...
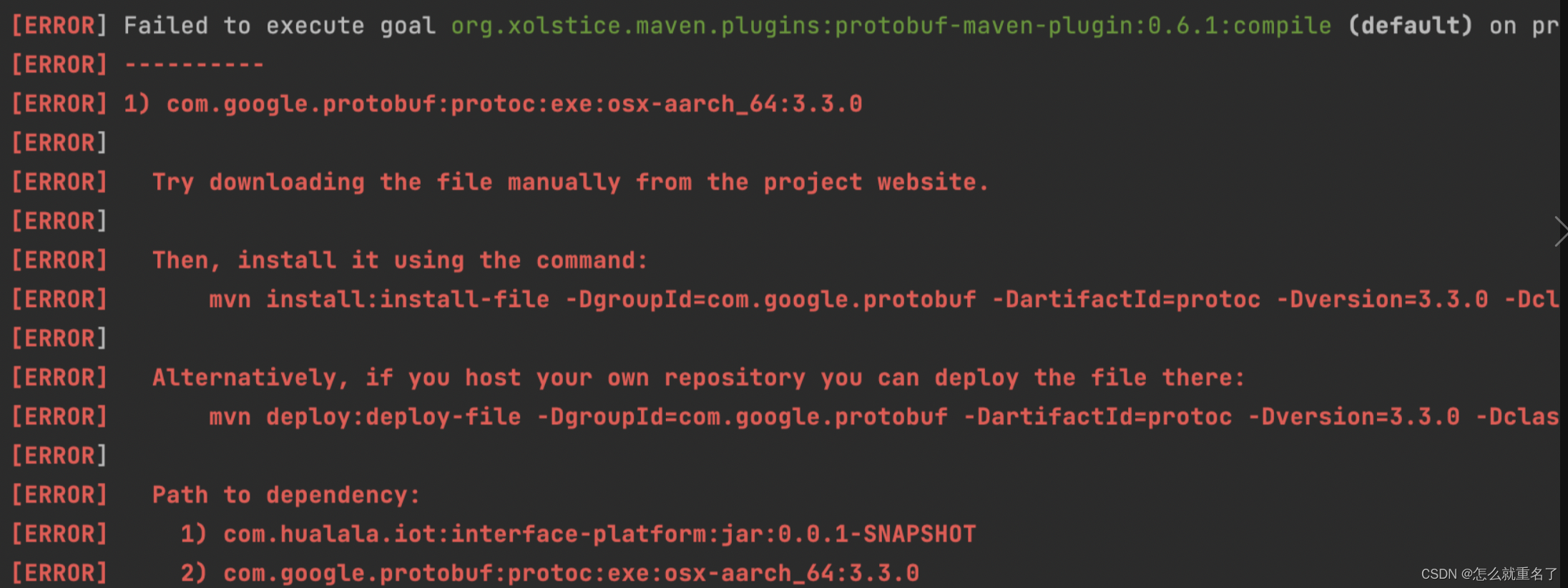
Mac上protobuf环境构建-java
参考文献 getting-started 官网pb java介绍 maven protobuf插件 简单入门1 简单入门2 1. protoc编译器下载安装 https://github.com/protocolbuffers/protobuf/releases?page10 放入.zshrc中配置环境变量 ~/IdeaProjects/test2/ protoc --version libprotoc 3.12.1 …...
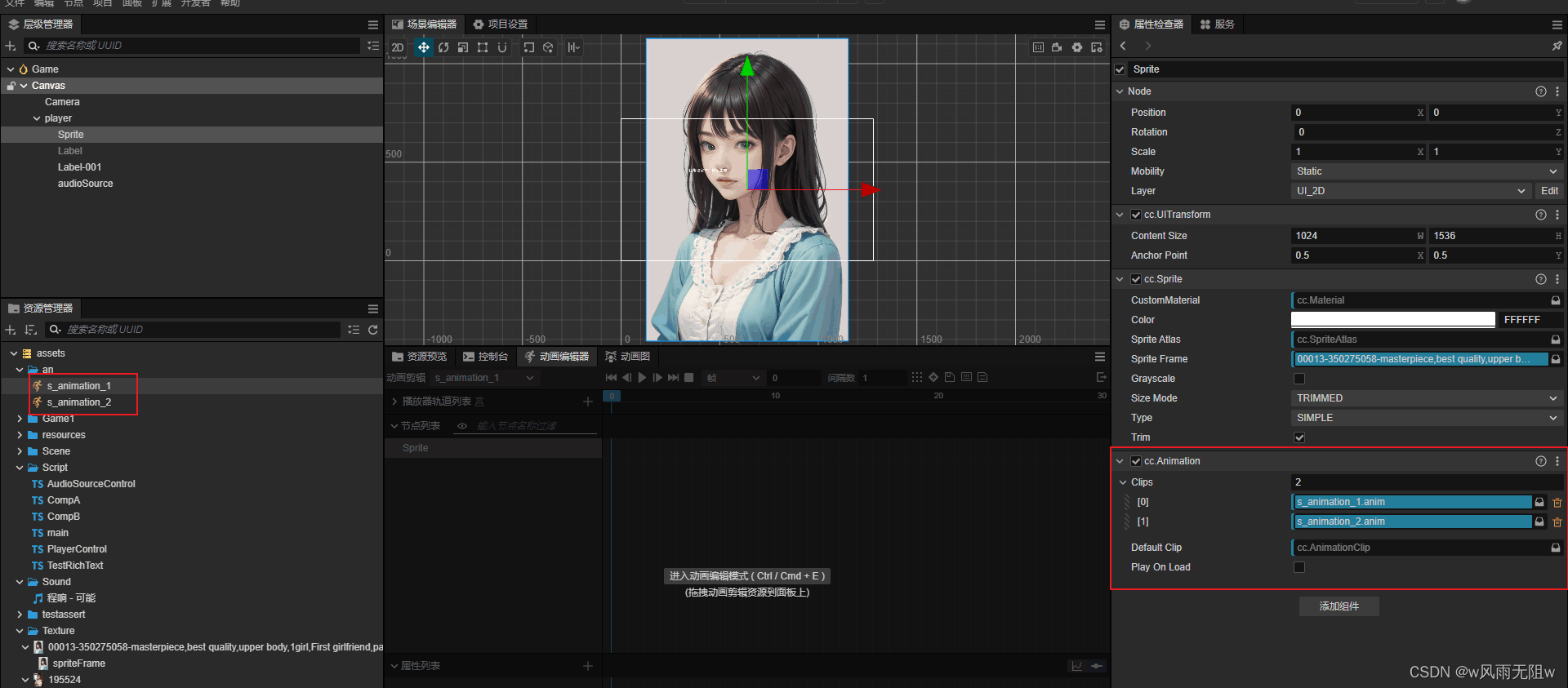
CocosCreator3.8研究笔记(二十二)CocosCreator 动画系统-动画剪辑和动画组件介绍
国庆假期,闲着没事,在家研究技术~ 大家都知道在Cocos Creator3.x 的版本的动画编辑器中,可以实现不用写一行代码就能实现各种动态效果。 Cocos Creator动画编辑器中主要实现关键帧动画,不仅支持位移、旋转、缩放、帧动画ÿ…...

信看课堂-厘米GNSS定位
我们常常说GPS 定位,不过定位远不止GPS定位,通过本节课程,我们将会了解到,原来GPS只是定位的一种: GNSS概述 不同的GNSS系统使用不同的频段来传输导航信号。以下是一些主要的GNSS系统及其相应的频段,用表…...
)
2023CCPC网络赛(A E)
2023CCPC网络赛(A E) The 2nd Universal Cup. Stage 3: Binjiang - Dashboard - Contest - Universal Cup Judging System A. Almost Prefix Concatenation 思路:首先考虑如何求出每个位置允许失配一次的LCP长度 , 可以二分哈希求LCP , 即…...

使用 python 检测泛洪攻击的案例
使用 python 检测泛洪攻击的案例 本案例只使用python标准库通过执行命令来监控异常请求, 并封锁IP, 不涉及其他第三方库工具. import os import time from collections import Counter# 1、update 命令, 采集CPU的平均负载 def get_cpu_load():"""uptime 命令…...

SCROLLINFO scrollInfo; 2023/10/5 下午3:38:53
2023/10/5 下午3:38:53 SCROLLINFO scrollInfo;scrollInfo.cbSize = sizeof(SCROLLINFO);scrollInfo.fMask = SIF_ALL;//scrollInfo.nMin = 0; // 最小位置//scrollInfo.nMax = nRowCountToShow; // 最大位置//scrollInfo.nPage = nRowCountToShow; // 页面大小//scrollInf…...

Python--控制台获取输入与正则表达式
前言一、控制台获取输入1.1 字符串输入1.2 整数输入1.3 浮点数输入1.4 布尔值输入1.5 列表输入1.6 汇总 二、正则表达式2.1 匹配数字2.2 模式检查2.3 替换字符2.4 切分字符串2.5 搜索并提取匹配的部分2.6 使用捕获组提取匹配的部分2.7 非贪婪匹配2.8 忽略大小写匹配2.9 使用预定…...
网络基础知识面试题1
VC++常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C++软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...)...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

