二分查找:34. 在排序数组中查找元素的第一个和最后一个位置

个人主页 : 个人主页
个人专栏 : 《数据结构》 《C语言》《C++》《算法》
文章目录
- 前言
- 一、题目解析
- 二、解题思路
- 1. 暴力查找
- 2. 一次二分查找 + 部分遍历
- 3. 两次二分查找分别查找左右端点
- 1.查找区间左端点
- 2. 查找区间右端点
- 三、代码实现
- 总结
前言
本篇文章仅是作为小白的我的一些理解,,如果有错误的地方,希望大佬们指出。
- 题目链接: 34. 在排序数组中查找元素的第一个和最后一个位置
一、题目解析
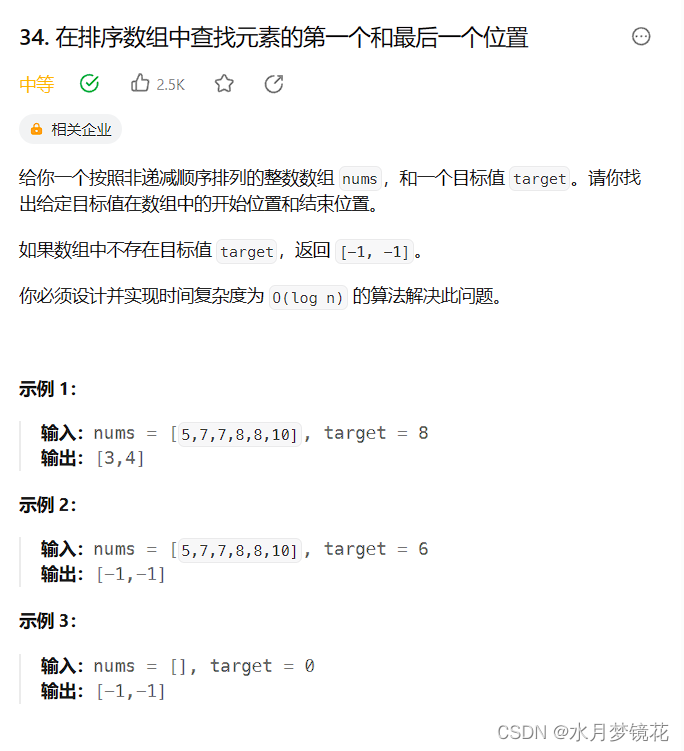
本题数组元素不唯一,可能存在多个target,我们就是要找到target区间中的左端点与右端点。

如果没有target区间,则返回{-1, -1}
二、解题思路
1. 暴力查找
直接遍历数组,如果可以查找到target则返回第一次与最后一次遇到target的下标,如果不能查找到target则返回{-1, -1}。
时间复杂度:O(n)
2. 一次二分查找 + 部分遍历
优先使用二分查找target,如果可以查找到,就从该下标开始向左向右遍历数组,返回最左边与最右边的target。如果不能查找到,返回{-1, -1}
时间复杂度:O(logn + n)
对于{3,3,3,3,3,3,3,3} target = 3,时间复杂度会退化为O(n)
3. 两次二分查找分别查找左右端点
1.查找区间左端点
我们对示例1使用 “ 二段性 ” 可以发现示例一被target分成了两部分,小于target部分{5, 7, 7}和大于等于target部分{8, 8, 10}。

如果中点mid到小于target的部分,区间[ left, mid ]这一区间都小于target,不可能是target区间的左端点,那么left = mid + 1;
如果中点mid到大于等于target的部分,区间[ mid, right ]这一区间都大于等于target, 其中mid有可能是target区间的左端点,那么right = mid;

细节处理:
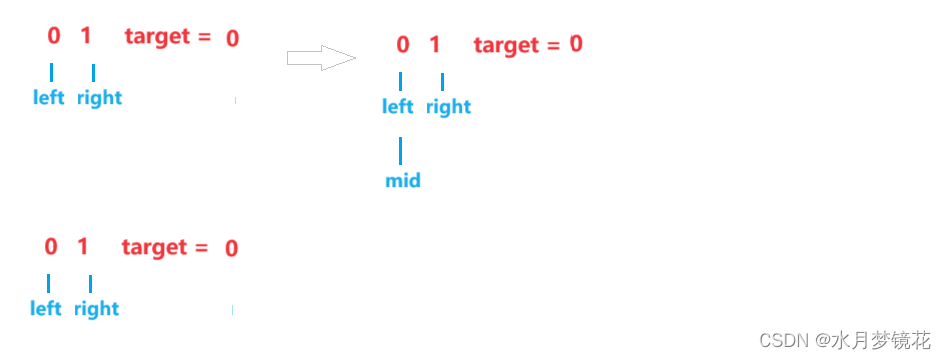
- 循环条件:left < right
如果循环条件为left <= right就会死循环。
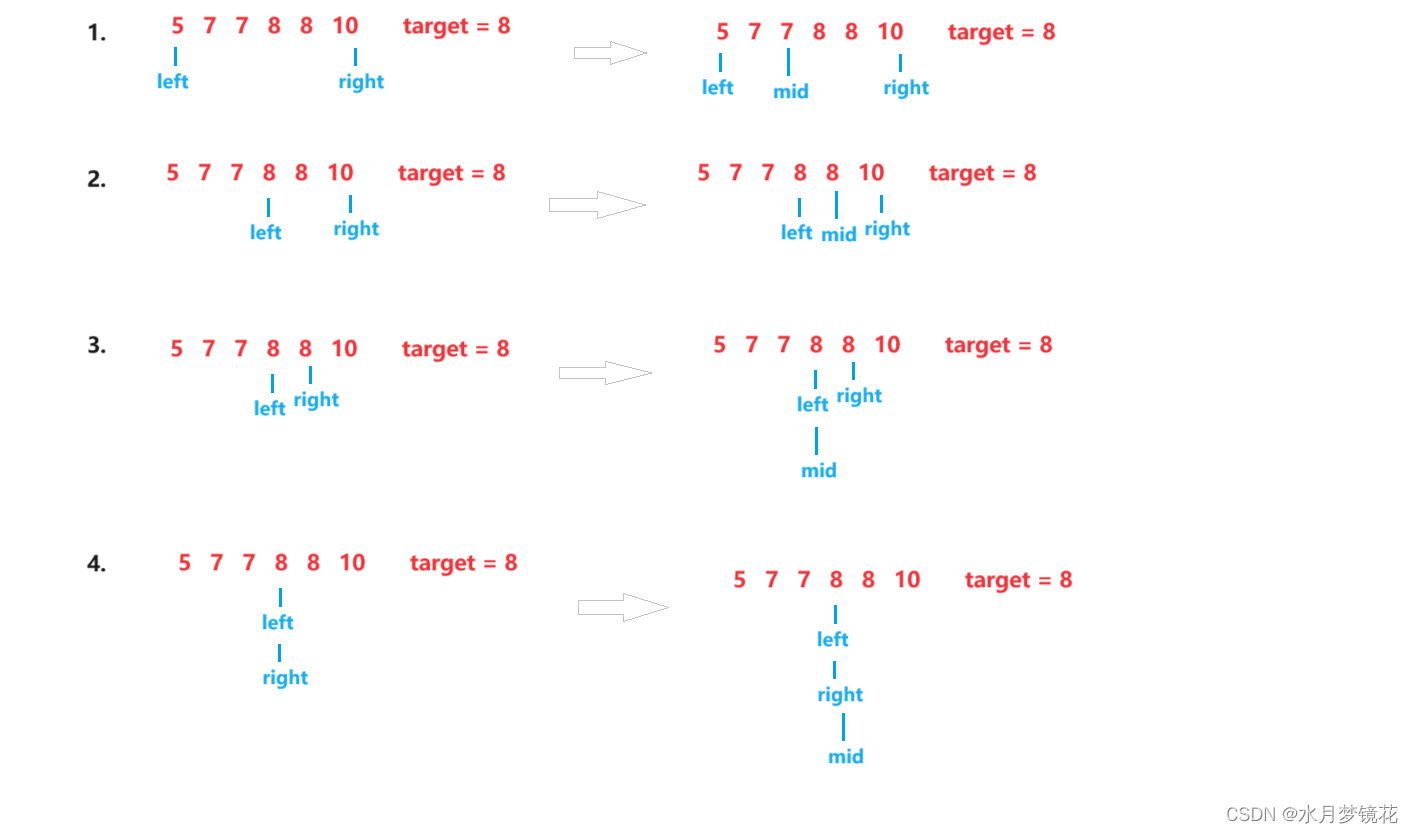
如上图4所示,nums[mid] >= target,right = mid。此时right依然与left指向同一个元素。
- 求mid的操作
向下取整:mid = left + (right - left)/2 向上取整:mid = left + (right - left + 1)/2;二者主要区别在与如果区间[ left, right]中的元素个数是偶数时,向下取整取的是中间两个数中左边的数,向上取整取的是中间两个数中右边的数。
此时查找区间左端点,求mid使用向上取整会导致死循环。
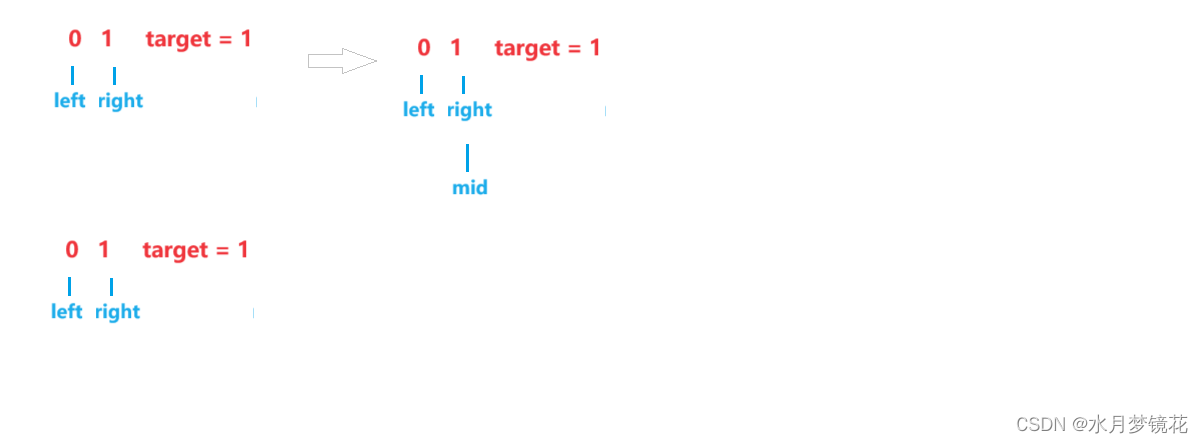
2. 查找区间右端点
查找区间右端点思路与查找区间左端点类似。
我们使用“二段性”发现示例一被target分成了两部分,小于等于target部分{5, 7, 7, 8, 8} 和大于target部分{10}。

如果点mid到小于等于target的部分,区间[ left, mid ] 这一区间都小于等于target,其中mid可能就是target区间的右端点,那么left = mid;
如果点mid到大于target的部分,区间[ mid, right ]这一区间都大于target,不可能是target区间的右端点,那么right= mid - 1;

细节处理:
-
循环条件:left < right, 理由与查找左端点使的循环条件相同,如果循环条件为left <= right会死循环
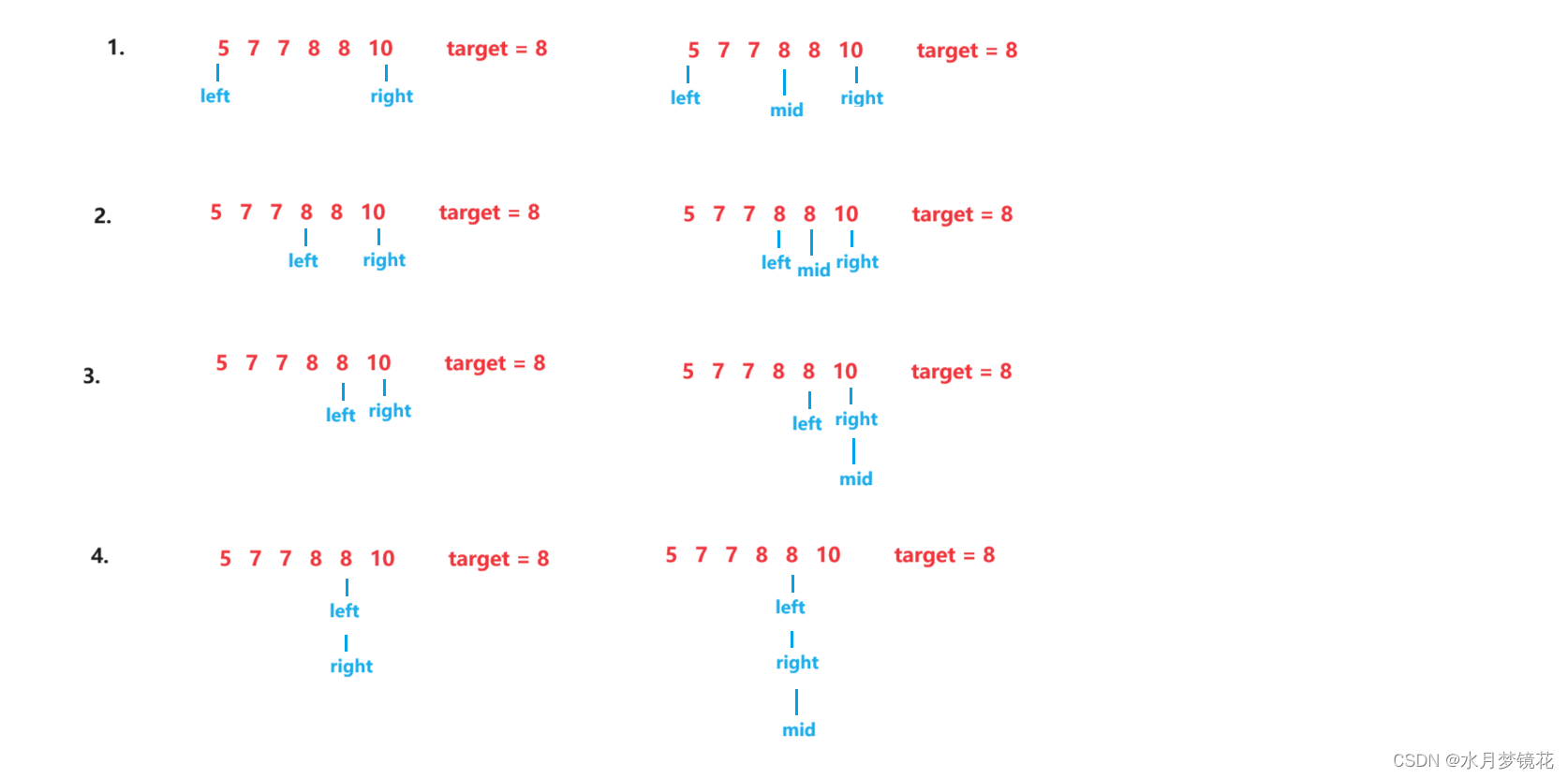
如上图4所示,nums[mid] <= target,left = mid, 此时left依然与right指向同一个元素。 -
求mid的操作,这里就要用向上取整的方法 mid = left + (right - left + 1)/2
此处查找区间右端点,如果使用向下取整会导致死循环
三、代码实现
两次二分查找分别查找左右端点
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {vector<int> ret({-1, -1});int n = nums.size();if(n == 0)return ret;int left = 0, right = n-1;// 查找左端点while(left < right){int mid = left + (right - left)/2;if(nums[mid] < target)left = mid+1;elseright = mid;}if(nums[right] == target)ret[0] = right;// 查找右端点left = 0, right = n-1;while(left < right){int mid = left + (right - left + 1)/2;if(nums[mid] > target)right = mid - 1;elseleft = mid;}if(nums[right] == target)ret[1] = right;return ret;}
};
总结
以上就是我对于在排序数组中查找元素的第一个和最后一个位置的理解。感谢支持!!!

相关文章:

二分查找:34. 在排序数组中查找元素的第一个和最后一个位置
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《算法》 文章目录 前言一、题目解析二、解题思路1. 暴力查找2. 一次二分查找 部分遍历3. 两次二分查找分别查找左右端点1.查找区间左端点2. 查找区间右端点 三、代码实现总结 前言 本篇文…...
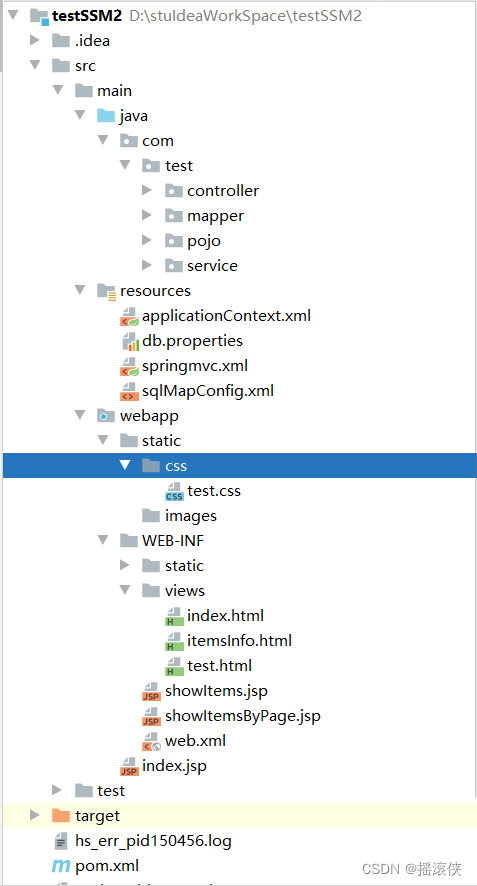
javaee ssm框架项目整合thymeleaf2.0 更多thymeleaf标签用法 项目结构图
创建ssmthymeleaf项目 创建ssmthymeleaf项目参考此文 thymeleaf更多常用标签 <!DOCTYPE html> <html lang"en" xmlns:th"http://www.thymeleaf.org"> <head><meta charset"UTF-8"><title>Title</title> …...

lv7 嵌入式开发-网络编程开发 11 TCP管理与UDP协议
目录 1 TCP管理 1.1 三次握手 1.2 四次挥手 1.3 保活计时器 2 wireshark安装及实验 3.1 icmp协议抓包演示 3.2 tcp协议抓包演示 3 UDP协议 3.1 UDP 的主要特点: 4 练习 1 TCP管理 1.1 三次握手 TCP 建立连接的过程叫做握手。 采用三报文握手࿱…...
overleaf在线编辑工具使用教程
文章目录 1 用 orcid注册overleaf获取模板2 使用模板 1 用 orcid注册overleaf获取模板 通常来说,在期刊投稿网站information for author中找template 。下载压缩包后上传到over leaf中。 加入找不到官方模板,用overleaf中的 2 使用模板 .bib文件&…...

Python基础复习【第一弹】【黑马】
本篇是观看b站黑马视频所做的笔记第一弹,为1-98节。 b站-黑马Python # 1.Hello World print("Hello World")# 2.字面量 在代码中,被写下来固定的值# 3.字符串 print("python")# 4.单行注释 # 多行注释""" "&q…...

【Word】公式编辑器中连字符/减号等显示偏长/过长
问题 当公式编辑器中出现连字符的时候,连字符显示偏长,如下图所示: 方法 在连字符的前后加上双引号后即可解决连字符显示偏长的问题。 最终效果对比如下: 结语 Word的公式编辑器中,双引号内部的内容被当做普通…...

架构设计系列4:如何设计高性能架构
在架构设计系列1:什么是架构设计中,我们讲了架构设计的主要目的,是为了解决软件系统复杂度带来的问题,今天我们来聊聊软件系统复杂度的来源之一高性能。 一、什么是高性能架构? 要搞清楚什么是高性能架构,…...

1392. 最长快乐前缀
链接: 1392. 最长快乐前缀 题解: class Solution { public:string longestPrefix(string s) {if (s.size() < 0) {return "";}int MOD 1e9 7;// 构建26的n次方,预处理std::vector<long> pow26(s.size());pow26[0] 1…...
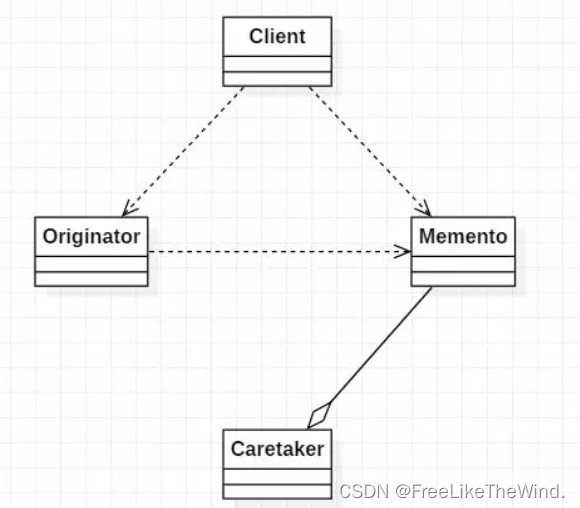
【C++设计模式之备忘录模式:行为型】分析及示例
简介 备忘录模式(Memento Pattern)是一种行为型设计模式,它用于保存和恢复对象的状态。备忘录模式通过将对象的状态封装成一个备忘录(Memento),并将备忘录保存在一个管理者(Caretakerÿ…...

数据结构与算法(四):哈希表
参考引用 Hello 算法 Github:hello-algo 1. 哈希表 1.1 哈希表概述 哈希表(hash table),又称散列表,其通过建立键 key 与值 value 之间的映射,实现高效的元素查询 具体而言,向哈希表输入一个键…...
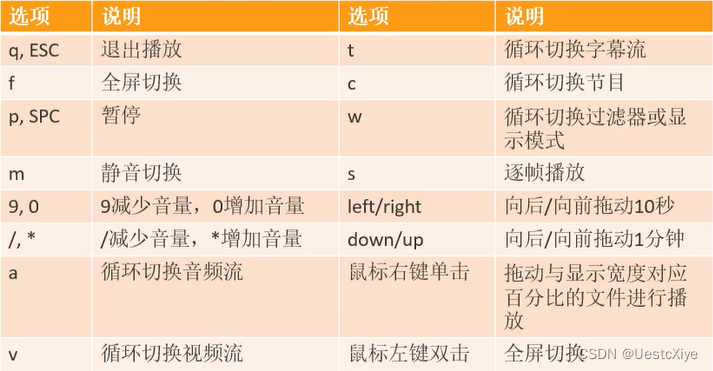
FFmpeg 命令:从入门到精通 | ffplay 播放控制选项
FFmpeg 命令:从入门到精通 | ffplay 播放控制选项 FFmpeg 命令:从入门到精通 | ffplay 播放控制选项选项表格图片 FFmpeg 命令:从入门到精通 | ffplay 播放控制选项 选项表格 项目说明Q,Esc退出播放F,鼠标左键双击全…...

代码随想录day59
647. 回文子串 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成&#…...
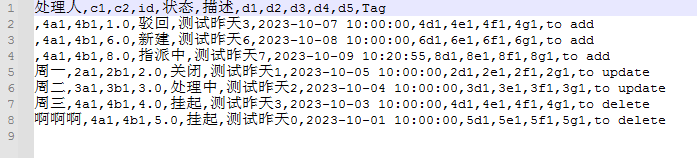
【小工具-生成合并文件】使用python实现2个excel文件根据主键合并生成csv文件
1 小工具说明 1.1 功能说明 一般来说,我们会先有一个老的文件,这个文件内容是定制好相关列的表格,作为每天的报告。 当下一天来的时候,需要根据新的报表文件和昨天的报表文件做一个合并,合并的时候就会出现有些事新增…...
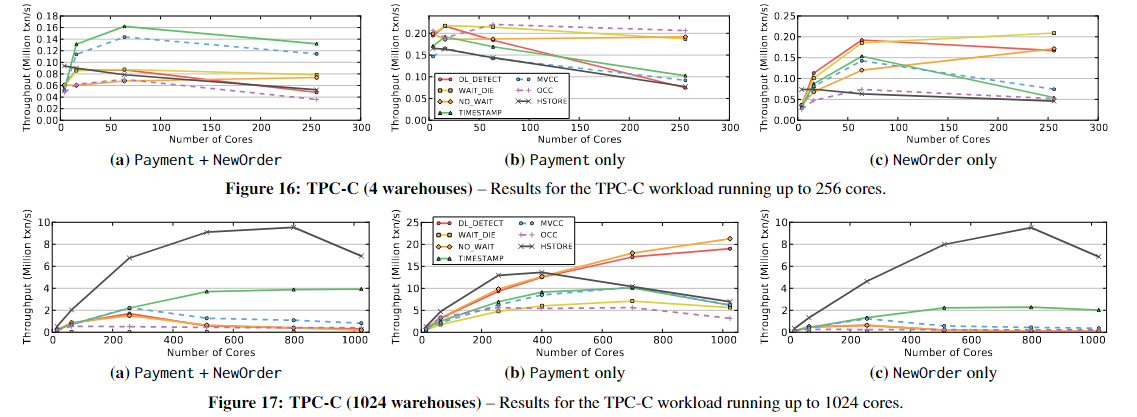
【论文阅读】An Evaluation of Concurrency Control with One Thousand Cores
An Evaluation of Concurrency Control with One Thousand Cores Staring into the Abyss: An Evaluation of Concurrency Control with One Thousand Cores ABSTRACT 随着多核处理器的发展,一个芯片可能有几十乃至上百个core。在数百个线程并行运行的情况下&…...
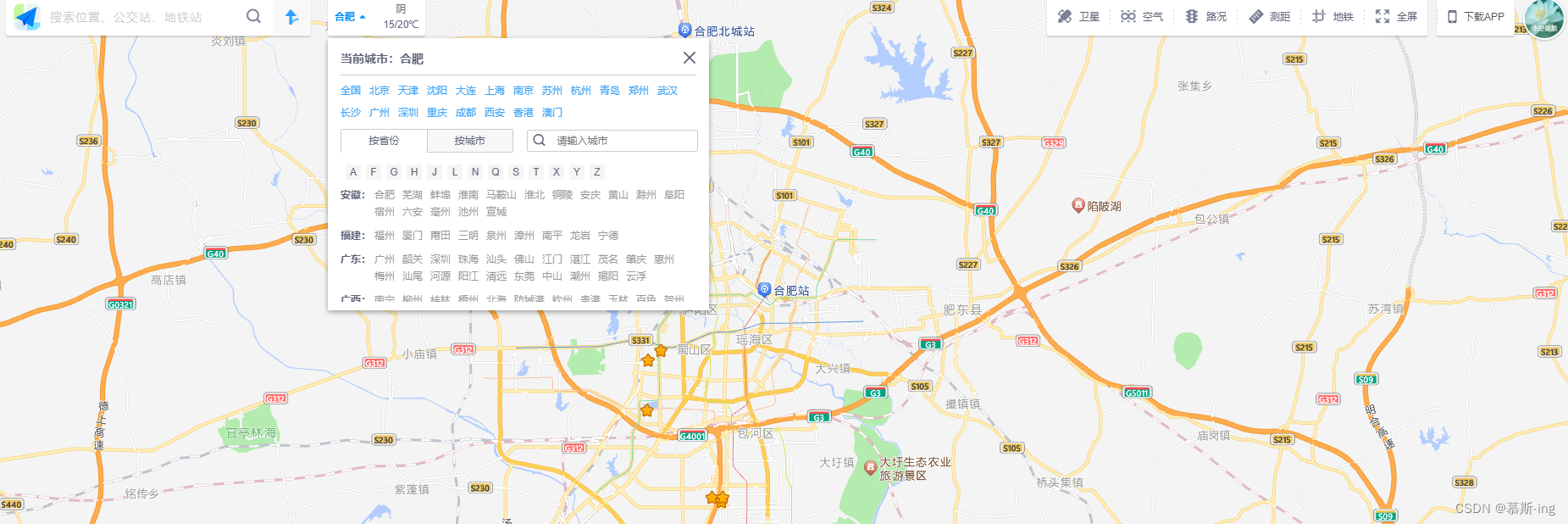
网页版”高德地图“如何设置默认城市?
问题: 每次打开网页版高德地图时默认定位的都是“北京”,想设置起始点为目前本人所在城市,烦恼的是高德地图默认的初始位置是北京。 解决: 目前网页版高德地图暂不支持设置起始点,打开默认都是北京,只能将…...

小谈设计模式(8)—代理模式
小谈设计模式(8)—代理模式 专栏介绍专栏地址专栏介绍 代理模式代理模式角色分析抽象主题(Subject)真实主题(Real Subject)代理(Proxy) 应用场景远程代理虚拟代理安全代理智能引用代…...

queryWrapper的使用教程
大于、等于、小于 eq 等于 例:queryWrapper.eq("属性","lkm") ——> 属性 lkm ne 不等于 例:queryWrapper.ne("属性","lkm") ——> 属性<> lkm gt 大于 例:queryWrapper.gt("属性…...

数组模拟双链表
文章目录 QuestionIdeasCode Question 实现一个双链表,双链表初始为空,支持 5 种操作: 在最左侧插入一个数; 在最右侧插入一个数; 将第 k 个插入的数删除; 在第 k 个插入的数左侧插入一个数; …...
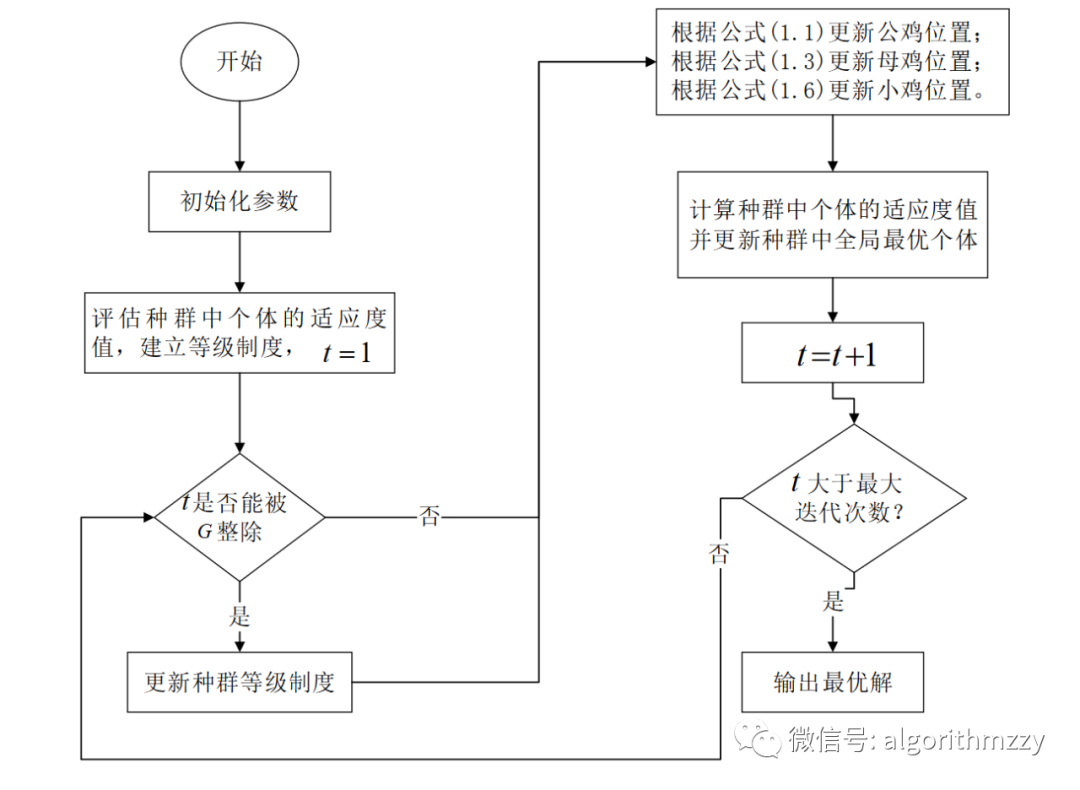
鸡群优化(CSO)算法(含MATLAB代码)
先做一个声明:文章是由我的个人公众号中的推送直接复制粘贴而来,因此对智能优化算法感兴趣的朋友,可关注我的个人公众号:启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法,经典的,或者是近几年…...
3. 安装lombok maven镜像设置
安装lombok & maven镜像设置 一、maven镜像设置 Maven:负责进行项目管理、依赖工具管理的 软件。 快捷解决方案: 1.方法一 直接配置系统默认的文件 各个人因为登录的用户名不同,所以目录名不同。 2.方法二 自定义本地仓库的位置 完成之后重新打…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
