acwing算法基础之基础算法--高精度加法算法
目录
- 1 知识点
- 2 模板
1 知识点
大整数 + 大整数,它们的长度都为 1 0 6 10^6 106。大整数是指长度为 1 0 6 10^6 106的整数。
大整数 - 大整数
大整数 * 小整数
大整数 / 小整数
把大整数存储到向量中,需要考虑高位在前还是低位在前,低位在前会更好一些。
2 模板
//A = [1,2,3,4]表示数4321
//B和C也是如此
vector<int> add(vector<int> &A, vector<int> &B) {vector<int> C;int t = 0;for (int i = 0; i < A.size() || i < B.size(); ++i) {if (i < A.size()) {t += A[i];}if (i < B.size()) {t += B[i];}C.emplace_back(t % 10);t /= 10;}if (t) {C.emplace_back(1);}return C;
}
相关文章:

acwing算法基础之基础算法--高精度加法算法
目录 1 知识点2 模板 1 知识点 大整数 大整数,它们的长度都为 1 0 6 10^6 106。大整数是指长度为 1 0 6 10^6 106的整数。 大整数 - 大整数 大整数 * 小整数 大整数 / 小整数 把大整数存储到向量中,需要考虑高位在前还是低位在前,低位在前…...

openGauss学习笔记-84 openGauss 数据库管理-内存优化表MOT管理-内存表特性-MOT部署服务器优化:x86
文章目录 openGauss学习笔记-84 openGauss 数据库管理-内存优化表MOT管理-内存表特性-MOT部署服务器优化:x8684.1 BIOS84.2 操作系统环境设置84.3 网络 openGauss学习笔记-84 openGauss 数据库管理-内存优化表MOT管理-内存表特性-MOT部署服务器优化:x86 …...

二分查找:34. 在排序数组中查找元素的第一个和最后一个位置
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《算法》 文章目录 前言一、题目解析二、解题思路1. 暴力查找2. 一次二分查找 部分遍历3. 两次二分查找分别查找左右端点1.查找区间左端点2. 查找区间右端点 三、代码实现总结 前言 本篇文…...
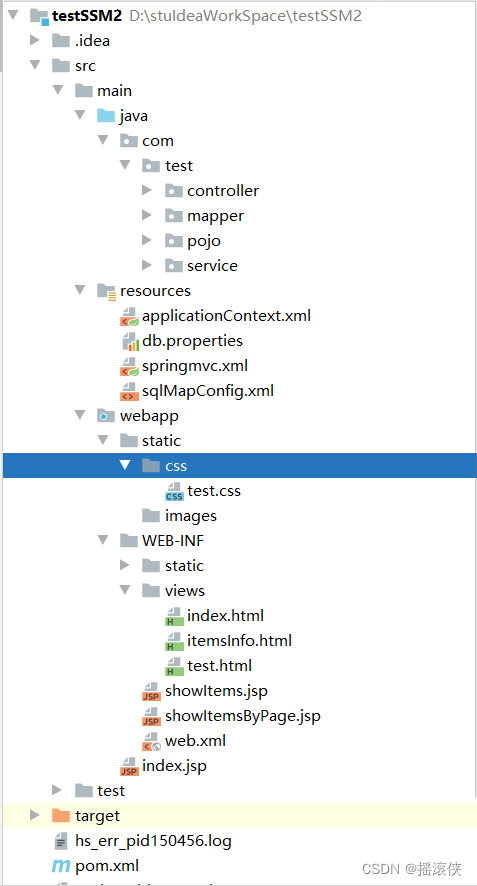
javaee ssm框架项目整合thymeleaf2.0 更多thymeleaf标签用法 项目结构图
创建ssmthymeleaf项目 创建ssmthymeleaf项目参考此文 thymeleaf更多常用标签 <!DOCTYPE html> <html lang"en" xmlns:th"http://www.thymeleaf.org"> <head><meta charset"UTF-8"><title>Title</title> …...

lv7 嵌入式开发-网络编程开发 11 TCP管理与UDP协议
目录 1 TCP管理 1.1 三次握手 1.2 四次挥手 1.3 保活计时器 2 wireshark安装及实验 3.1 icmp协议抓包演示 3.2 tcp协议抓包演示 3 UDP协议 3.1 UDP 的主要特点: 4 练习 1 TCP管理 1.1 三次握手 TCP 建立连接的过程叫做握手。 采用三报文握手࿱…...
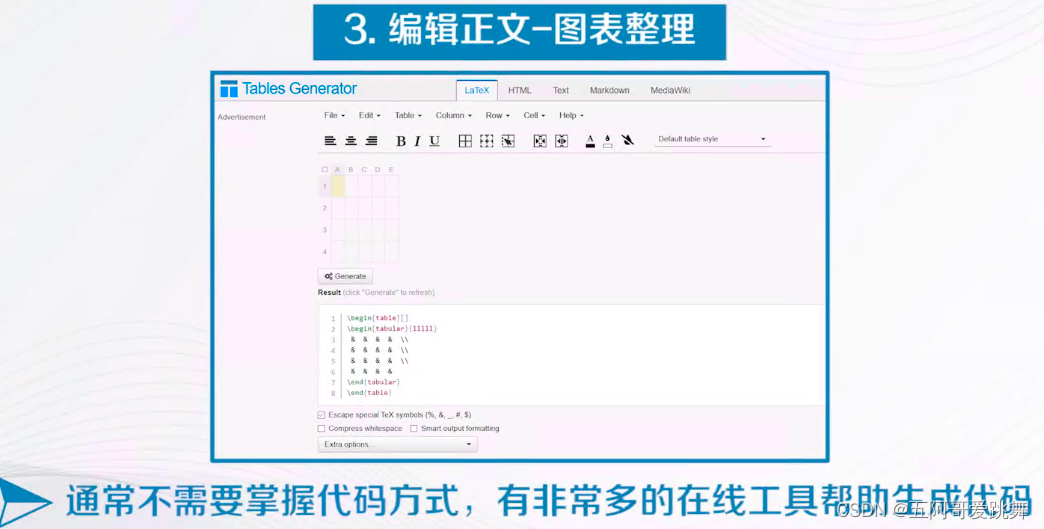
overleaf在线编辑工具使用教程
文章目录 1 用 orcid注册overleaf获取模板2 使用模板 1 用 orcid注册overleaf获取模板 通常来说,在期刊投稿网站information for author中找template 。下载压缩包后上传到over leaf中。 加入找不到官方模板,用overleaf中的 2 使用模板 .bib文件&…...

Python基础复习【第一弹】【黑马】
本篇是观看b站黑马视频所做的笔记第一弹,为1-98节。 b站-黑马Python # 1.Hello World print("Hello World")# 2.字面量 在代码中,被写下来固定的值# 3.字符串 print("python")# 4.单行注释 # 多行注释""" "&q…...

【Word】公式编辑器中连字符/减号等显示偏长/过长
问题 当公式编辑器中出现连字符的时候,连字符显示偏长,如下图所示: 方法 在连字符的前后加上双引号后即可解决连字符显示偏长的问题。 最终效果对比如下: 结语 Word的公式编辑器中,双引号内部的内容被当做普通…...

架构设计系列4:如何设计高性能架构
在架构设计系列1:什么是架构设计中,我们讲了架构设计的主要目的,是为了解决软件系统复杂度带来的问题,今天我们来聊聊软件系统复杂度的来源之一高性能。 一、什么是高性能架构? 要搞清楚什么是高性能架构,…...

1392. 最长快乐前缀
链接: 1392. 最长快乐前缀 题解: class Solution { public:string longestPrefix(string s) {if (s.size() < 0) {return "";}int MOD 1e9 7;// 构建26的n次方,预处理std::vector<long> pow26(s.size());pow26[0] 1…...
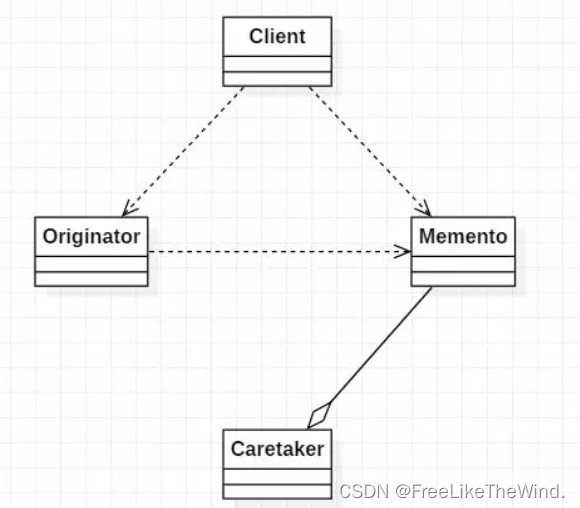
【C++设计模式之备忘录模式:行为型】分析及示例
简介 备忘录模式(Memento Pattern)是一种行为型设计模式,它用于保存和恢复对象的状态。备忘录模式通过将对象的状态封装成一个备忘录(Memento),并将备忘录保存在一个管理者(Caretakerÿ…...

数据结构与算法(四):哈希表
参考引用 Hello 算法 Github:hello-algo 1. 哈希表 1.1 哈希表概述 哈希表(hash table),又称散列表,其通过建立键 key 与值 value 之间的映射,实现高效的元素查询 具体而言,向哈希表输入一个键…...
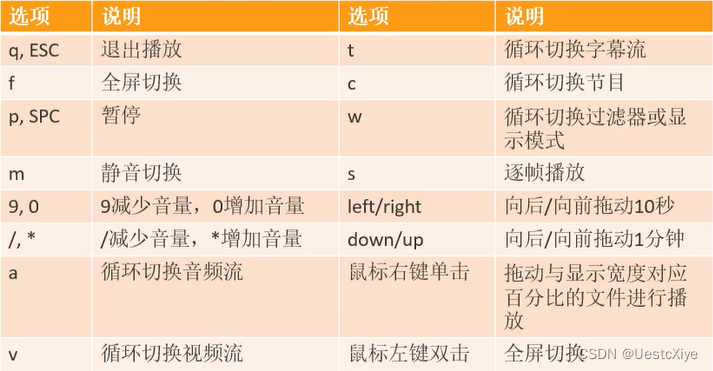
FFmpeg 命令:从入门到精通 | ffplay 播放控制选项
FFmpeg 命令:从入门到精通 | ffplay 播放控制选项 FFmpeg 命令:从入门到精通 | ffplay 播放控制选项选项表格图片 FFmpeg 命令:从入门到精通 | ffplay 播放控制选项 选项表格 项目说明Q,Esc退出播放F,鼠标左键双击全…...

代码随想录day59
647. 回文子串 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成&#…...
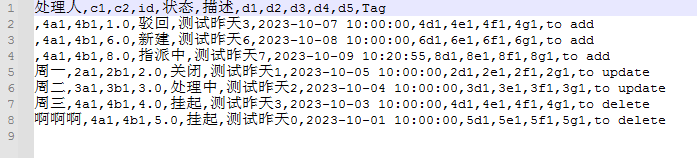
【小工具-生成合并文件】使用python实现2个excel文件根据主键合并生成csv文件
1 小工具说明 1.1 功能说明 一般来说,我们会先有一个老的文件,这个文件内容是定制好相关列的表格,作为每天的报告。 当下一天来的时候,需要根据新的报表文件和昨天的报表文件做一个合并,合并的时候就会出现有些事新增…...
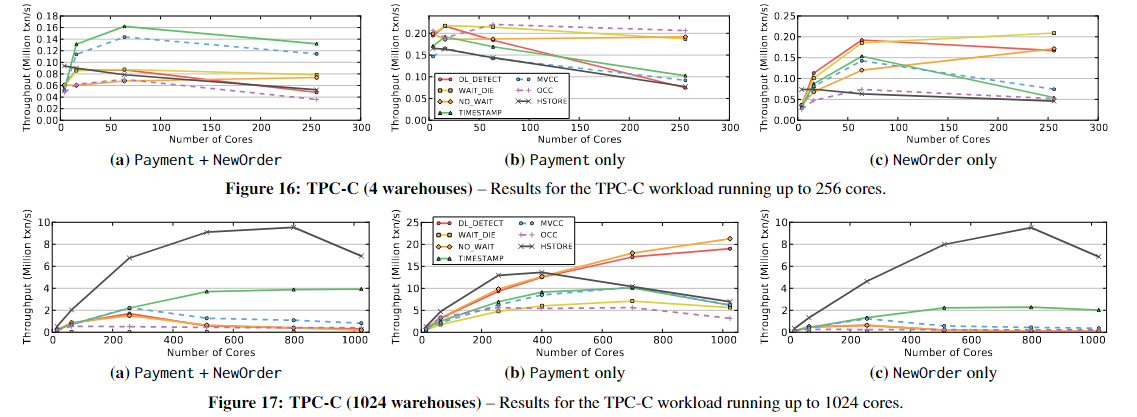
【论文阅读】An Evaluation of Concurrency Control with One Thousand Cores
An Evaluation of Concurrency Control with One Thousand Cores Staring into the Abyss: An Evaluation of Concurrency Control with One Thousand Cores ABSTRACT 随着多核处理器的发展,一个芯片可能有几十乃至上百个core。在数百个线程并行运行的情况下&…...
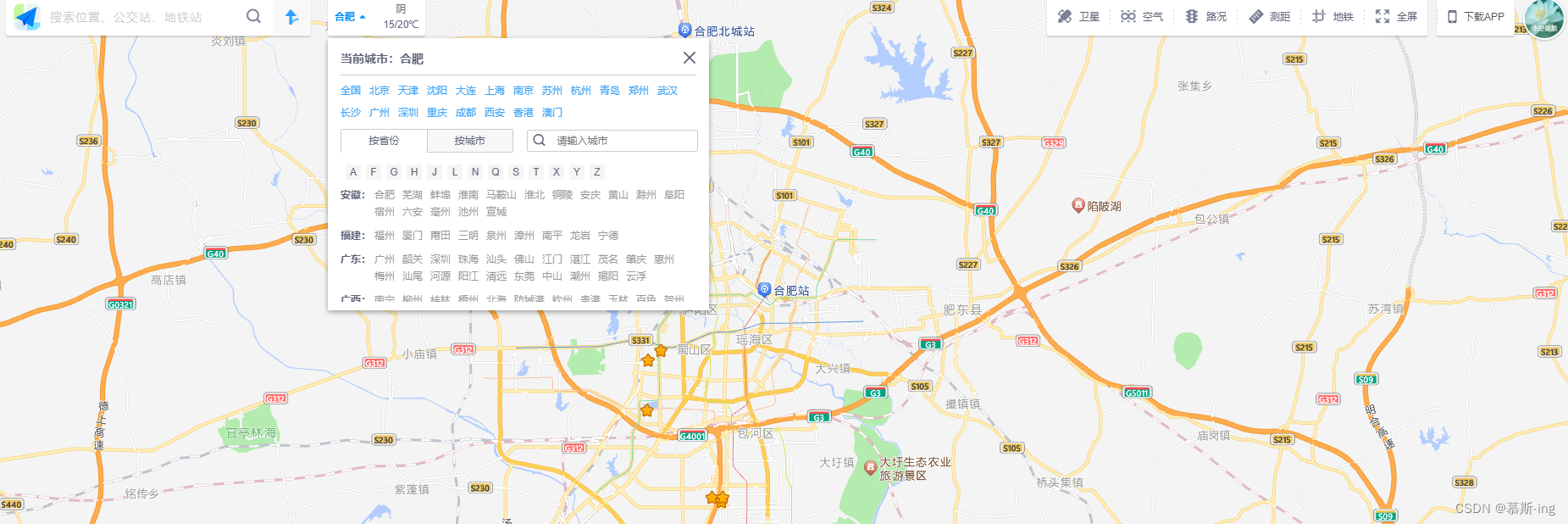
网页版”高德地图“如何设置默认城市?
问题: 每次打开网页版高德地图时默认定位的都是“北京”,想设置起始点为目前本人所在城市,烦恼的是高德地图默认的初始位置是北京。 解决: 目前网页版高德地图暂不支持设置起始点,打开默认都是北京,只能将…...

小谈设计模式(8)—代理模式
小谈设计模式(8)—代理模式 专栏介绍专栏地址专栏介绍 代理模式代理模式角色分析抽象主题(Subject)真实主题(Real Subject)代理(Proxy) 应用场景远程代理虚拟代理安全代理智能引用代…...

queryWrapper的使用教程
大于、等于、小于 eq 等于 例:queryWrapper.eq("属性","lkm") ——> 属性 lkm ne 不等于 例:queryWrapper.ne("属性","lkm") ——> 属性<> lkm gt 大于 例:queryWrapper.gt("属性…...

数组模拟双链表
文章目录 QuestionIdeasCode Question 实现一个双链表,双链表初始为空,支持 5 种操作: 在最左侧插入一个数; 在最右侧插入一个数; 将第 k 个插入的数删除; 在第 k 个插入的数左侧插入一个数; …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
